无限维齐性Rota-Baxter 3-李代数(Ⅰ)
2022-01-14白瑞蒲刘山
白瑞蒲,刘山
(1.河北大学 数学与信息科学学院, 河北 保定 071002;2.河北省机器学习与智能计算重点实验室,河北 保定 071002 )
3-李代数[1-4]A是域F上具有线性运算[,,]:A^3→A的线性空间, 且对任意x1,x2,x3,y2,y3∈A,满足下列恒等式
[[x1,x2,x3],y2,y3]=[[x1,y2,y3],x2,x3]+[x1,[x2,y2,y3],x3]+[x1,x2,[x3,y2,y3]].
设A是域F上的3-李代数,R是A上的F-线性映射, 如果对λ∈F, 等式
[R(x1),R(x2),R(x3)]=R{[R(x1),R(x2),x3]+[R(x1),x2,R(x3)]+[x1,R(x2),R(x3)]+
λ[R(x1),x2,x3]+λ[x1,R(x2),x3]+λ[x1,x2,R(x3)]+λ2[x1,x2,x3]}
(1)
成立, 则称R是3-李代数A上权为λ的Rota-Baxter算子[3-5], 称(A,[,,],R)为权为λ的Rota-Baxter 3-李代数.

引理1[3]设(A,[,,],R)为权为λ的Rota-Baxter 3-李代数, 则(A,[,,]R,R)为权为λ的Rota-Baxter 3-李代数, 其中[,,]R:A^3→A满足∀x1,x2,x3∈A,
[x1,x2,x3]R=[R(x1),R(x2),x3]+[R(x1),x2,R(x3)]+[x1,R(x2),R(x3)]+
λ[R(x1),x2,x3]+λ[x1,R(x2),x3]+λ[x1,x2,R(x3)]+λ2[x1,x2,x3].
(2)
在本文的讨论中, 全体整数集合记为Z.文献[4]中, 利用无限维交换的结合代数构造出单的无限维3-李代数Aω, 其中{Ln|n∈Z}为Aω的一组基, 域F为复数域, 其运算为
对Aω上权为λ的Rota-Baxter算子R, 如果存在可加映射h:Z→F使得
R(Lm)=h(m)Lm,∀m∈Z,
(3)
则称R是3-李代数Aω上权为λ的齐性Rota-Baxter算子[6-10]. 文献[5]中研究了3-李代数Aω上权为1的齐性Rota-Baxter算子. 在Aω基空间上由齐性Rota-Baxter算子按照引理1构造的3-李代数称为齐性Rota-Baxter 3-李代数.
本文要利用齐性Rota-Baxter算子构造3-李代数. 为此, 需要首先对文献[5]的结论进行修正. 为方便起见,在以下的讨论中, 记Z+={m|m∈Z,m≥0},且在3-李代数的乘法表中, 省略掉乘积等于零的基向量运算.
主要结论
定理1Aω上权为1且满足h(0)+h(1)+1≠0的齐性Rota-Baxter算子如下:
R1(Lm)=0;R2(Lm)=-Lm,∀m∈Z;
其中α∈F≠-1,B∈F≠0,m0∈Z.
证明:由文献[5]中定理3.5可得R1,R2,R3,R4,R5和R6.设R为式(3)中定义的线性映射, 由式(1)知R为Aω上权为1且满足h(0)+h(1)≠0的齐性Rota-Baxter算子当且仅当下列等式成立, 对∀m,n,k∈Z,m≠n,
h(2m)h(2n)h(2k+1)=h(2m+2n+2k)(h(2m)h(2n)+h(2m)h(2k+1)+
h(2n)h(2k+1)+h(2m)+h(2n)+h(2k+1)+1),
(4)
h(2m+1)h(2n+1)h(2k)=h(2m+2n+2k+1)(h(2m+1)h(2n+1)+h(2m+1)h(2k)+
h(2n+1)h(2k)+h(2m+1)+h(2n+1)+h(2k)+1).
(5)
由文献[5]中定理3.7、定理3.8以及定理3.10, 如果R满足: 存在m0,m1∈Z,m0
定理2设V是3-李代数Aω的基空间, 则在V上以Aω上权为1且满足h(0)+h(1)+1=0的齐性Rota-Baxter算子按照引理1构造的3-李代数在同构的意义下有且仅有如下5类:
C1:Aω;
C2:[L0,L2k1+1,L2k2+1]C2=4(k2-k1)L2(k1+k2)+1,∀k1,k2∈Z;
证明:记由齐性Rota-Baxter算子Rk构造的齐性Rota-Baxter 3-李代数为Ak, 即Ak=(A,[,,]k,Rk),k=1,2,…,20.在以下讨论中设α∈F≠-1,b∈F≠0,m0∈Z均为常数.由定理1及等式(2)可知A1与A2即是Aω,得到代数C1.
直接计算可知线性变换φs:As→C2,s=3,4,5,6是代数同构, 其中

线性变换φ13:A13→C3(n0=1),线性变换φs:As→C3(n0=2),s=7,9,10与线性变换φ15:A15→C3(n0=3)是代数同构, 且代数A16与代数C3(n0=3)相同, 其中
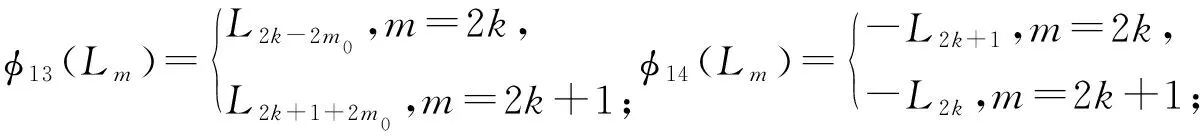
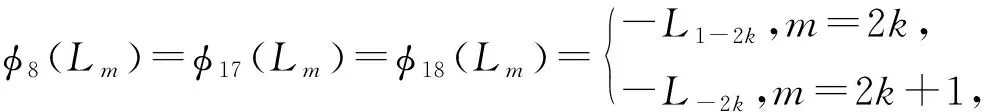
由定理 1及式(2)可知A19与A20是代数C5.
下面证明代数Ci不同构Cj,1≤i≠j≤5.记3-李代数Ck的中心为Z(Ck),k=1,2,…,5.由乘法表知Z(C1)=Z(C3)=Z(C4)=Z(C5)=0且Z(C2)={L2k|k≠0,k∈Z}≠0,故C2和C1,C3,C4,C5不同构;C1为单的3-李代数, 直接计算可知C3的导代数余空间维数为8,C4(n1=2)的导代数余空间维数为6,C4(n1=3) 的导代数余空间维数为4,C5的导代数是C5,且C5有真理想I=〈L1+4kL4k|k∈Z〉,故C1,C3,C4,C5互相之间不同构.证毕.
定理33-李代数C2是具有非零中心的可分解3-李代数, 且C2=Z(C2)⊕I,其中C(C2)=〈L2k|k∈Z,k≠0〉,I=〈L0,L2k+1|k∈Z〉.
证明:应用定理 2可得结论.省略计算过程.证毕.
定理43-李代数C4(n1=2,3)可唯一分解为理想I4和J4的直和,即C4=I4⊕J4, 其中J4=〈Ln1,Lm|m∈Z,m<0〉,I4=〈Lm|m≠n1,m≥0,m∈Z〉.
证明:易见I4和J4为C4的理想且C4=I4⊕J4.下面证明分解的唯一性.

定理53-李代数C5可分解为理想I5和J5的直和, 即C5=I5⊕J5,其中I5=〈L1+4m,l4m|m∈Z〉,J5=〈L3+4m,l2+4m|m∈Z〉且I5与J5均与代数Aω同构.
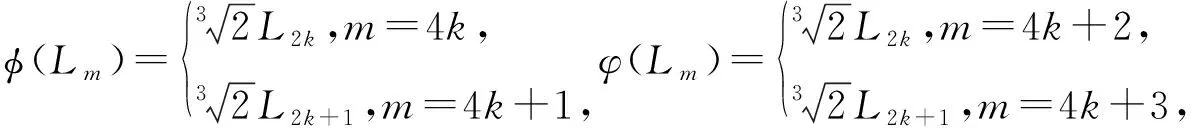
定理63-李代数C3(n0=1,2,3)可唯一分解为理想I3和J3的直和, 即C3=I3⊕J3, 其中I3=〈Lm|m∈Z,m≥n0〉,J3=〈Lm|m∈Z,m 证明:显然C3=I3⊕J3,且I3和J3是理想.对n0=1,2,3时分别计算I3与J3的下降中心列, 且进行与定理 4完全类似的讨论, 可得对n0=1,2,3时对应的3-李代数彼此之间不同构且分解式唯一.证毕.
