基于改进狼群算法的多机协同目标分配研究

陈 杰,薛雅丽,叶金泽

(南京航空航天大学 自动化学院,南京211106)

0 引 言

近年来,随着智能化的不断发展,单架飞机在现代复杂战场中所发挥的作战效能逐步减弱,多机协同作战理念逐渐成为主流思想。多机协同作战是指多架战机以配合协作的方式共同完成空中战斗任务,以达到更好的战场收益。其中,多目标火力分配问题是多机协同作战中一个重要问题,其解空间会随着目标总数和战机数目的增加而呈指数级递增[1-2]。许多研究者针对目标火力分配问题提出了许多模型求解算法。2002年,Lee等[3]采用基于免疫的蚁群算法对战场防空武器目标分配问题进行了研究。2006年,罗德林等[4]设计了一种局部搜索算法,并将其与蚁群算法融合,提高了蚁群算法在应用于空战目标分配时对全局最优解的搜索效率。目前解决该领域问题的算法主要是以一种智能算法为主,结合另一种或多种智能算法的混合优化算法,或是在原有的算法基础上做出了较大的改进。如2015年朱德法等[5]采用改进粒子群算法设计了新的粒子群位置和速度更新过程,能更快速解决多机协同作战的目标分配问题。2016年,孔德鹏等[6]通过改进人工蜂群算法对武器目标分配模型进行求解,采用了新型轮盘赌选择策略、多维搜索等方式,最终改善了算法的收敛性和寻优性能。2019年,张永利等[7]采用线性规划方法解决了舰空火力分配问题。

狼群算法最早被Liu等[8]在2011年提出,根据狼群觅食特点分为3种智能行为:搜索、围攻和更新。并且将狼群算法与粒子群算法、遗传算法等相比较,发现狼群算法具有求解最优值的精度更高、速度更快以及涉及参数更少等优点。当将狼群算法引入目标分配决策问题求解时,其还具备有高鲁棒性的优点。但狼群算法也有不少缺点,比如全局掌控性不高,个体之间交流较少且分散,易导致算法陷入局部最优。笔者基于传统狼群算法(WPA:Wolf Pack Algorithm)[9]提出改进策略,针对WPA中存在的寻优精度低、易陷入局部最优问题,对狼群召唤、围攻行为机制进行改进,并引入了双-头狼机制,通过双-头狼随机选择人工狼部下的方法增强了算法跳出局部最优问题的能力。同时加大了次头狼的搜索范围,以改善算法的全局搜索能力。将这种新的双-头狼狼群算法(DLWPA:Double-Leader Wolf Pack Algorithm)应用于飞机目标火力分配问题,构建了空战战场火力分配数学模型,并给出了改进算法的实现流程,最后通过仿真实验验证了该方法的可行性和有效性。

1 构建空战态势目标分配数学模型

针对多目标火力分配问题,笔者对空中战场态势进行如下假设。

我方i架战斗机,敌方目标战斗机j架,当j＜i时,我方占据战场优势,此时运用寻优算法为目标火力分配进行决策的收益较低,难以体现出算法价值。笔者主要研究对象为在战场中我方战机数目小于敌方战机数目的情况下如何通过寻优算法求解最优火力分配决策,故而设定条件j＞i。每架战斗机为一个作战单元,其仅携带一种火力载荷,该条件表示每架我方战斗机对各敌方目标的杀伤概率为确定值P=pij,其中pij表示第i架我方战斗机对第j架敌方目标战斗机的杀伤概率;在单次打击行为中,一架我方战斗机只能毁伤一个敌方目标,每个敌方目标最多只能分配k架我方战斗机进行攻击,各敌方目标的毁伤收益为确定值W=Wj,其中Wj表示第j个敌方目标战斗机的毁伤收益值。

1)目标打击约束。每架我方战斗机必须分配1个打击目标。至多分配2架我方战斗机打击同一目标,即0≤k≤2。

2)有效杀伤约束。针对敌方目标j,仅当对其的综合杀伤概率大于预设的杀伤概率阈值时可以认定该次打击为有效打击,即Pg≥P阈。当Pg＜P阈时,认定该次打击为无效打击,此时针对目标j的打击收益值为0,即此时Fj=0。

3)当两个不同的目标火力分配策略所取得的目标价值收益值F相同时,选取其中对高毁伤收益目标打击数量更多的分配策略为最优策略[11]。

2 传统狼群算法

2.1 狼群算法

传统狼群算法通过模拟自然界中狼群相互协作,捕食猎物的行为处理优化问题。算法中主要包括两个准则和3种智能行为,分别为“胜者为王”的头狼产生规则和“适者生存”的狼群更新原则以及探狼游走、头狼召唤和猛狼围攻3种行为[12-13]。在WPA算法中,通过目标函数值大小构建猎物解空间,狼群在解空间中分工合作,以各种搜寻方式寻找最优目标进而完成捕杀任务。在狼群算法的分工中,头狼位置代表当前所发现的最优目标位置,头狼本身不进行移动,而是指挥猛狼向自身位置奔袭;探狼根据嗅到的猎物目标气息浓度判断是否向猎物方向靠近,并将搜寻信息告知头狼;猛狼在接收到头狼召唤信号后向头狼所在位置发起奔袭,到达头狼附近后所有猛狼向猎物目标区域发起围攻行为[14]。狼群算法捕猎模型图如图1所示。

图1 狼群算法捕猎模型图Fig.1 Hunting model diagram of wolf pack algorithm

2.2 求解目标分配问题的狼群算法

围绕狼群算法在空中战场态势模型中的应用,笔者借鉴了文献[10]中求解火力分配问题的设计方案。首先给出目标分配问题算法描述,在求解应用于目标分配问题的WPA算法中采用整数编码的形式重新定义目标解空间,进而重新设计游走、召唤、围攻算子以及狼群更新机制和头狼产生规则,最终实现智能优化算法求解空战目标分配问题。具体设计如下[10,15]。

假定目前战场上有n架我方战机和m架敌方战机(其中n＜m),则可设定人工狼(除头狼外的所有狼群个体视为人工狼)的位置矢量维度为m,狼群的总数为N。故在N×m的欧氏空间中,第i匹人工狼的位置为Xi=(xi1,xi2,…,xij,…,xin),其中xij表示第i匹人工狼在第j维变量空间中所处的位置,其取值范围为1~m之间的整数。xij=t表示第j架我方战机攻击第t架敌方战机,故而可以用每匹人工狼的位置代表一种目标分配候选方案,人工狼位置的变换即代表目标分配方案的更替,算法最终目的为解算出最优的头狼位置。

由式(2)可知,为判别人工狼感知到的猎物气味浓度大小,引入目标函数值F。在猎物解空间中,每个位置的F值大小代表着当前目标分配方案的优劣。并且采用曼哈顿距离计算方式表示两只人工狼之间的距离,例如人工狼p与人工狼q之间的距离

1)头狼产生规则。狼群算法中具备最高目标函数值的人工狼为头狼。算法迭代过程中根据各人工狼的目标函数值大小执行贪婪决策,头狼本身不执行游走和围攻行为。

2)游走行为。在算法选出头狼后,剩余所有人工狼视为探狼。游走次数为T,这表示游走行为中探狼以游走步长a向自身周围T个方向试探前进,也可认为是对探狼当前位置执行T次游走算子Θ(Xi,Ra,a),以下为对游走算子的定义。

根据所得T个新位置的目标函数值进行贪婪决策。若游走后探狼所在位置目标函数值大于头狼目标函数值,则更新头狼位置,否则继续游走行为直至达到最大游走次数。

3)召唤行为。当所有探狼执行完游走行为后,视除头狼外所有探狼为猛狼。头狼向所有猛狼发起召唤行为,猛狼以较大的奔袭步长b向头狼位置前进。即对猛狼当前位置执行1次召唤算子Φ(Xi,Rb,b),以下为对召唤算子的定义。

针对召唤算子Φ(Xi,Rb,b),人工狼i的位置为Xi=(xi1,xi2,…,xij,…,xin),Rb为人工狼i位置Xi与头狼位置XL不相同编码位的集合,b为召唤步长。召唤算子表示在集合Rb中随机选择b个编码位,使人工狼Xi中被选中的编码位的值与头狼XL中相应位置的值相等。例如,设召唤算子Φ(Xi,Rb,2),其中Xi=(3,5,2,7,1),头狼位置为XL=(1,5,2,6,4),故可得Rb={1,4,5}。设随机选中的编码位集合

若猛狼在前进途中其所在位置的目标函数值大于头狼目标函数值,则更新头狼位置,并在新位置重新发起召唤,否则猛狼继续前进直到猛狼与头狼距离小于阈值距离dnear。

4)围攻行为。召唤行为会将所有猛狼集中至头狼附近。当所有猛狼停下前进动作后头狼会发起围攻行为指令,以头狼所在位置为猎物位置,猛狼以较小的围攻步长c向目标位置发起围攻,猛狼i的位置依照

3 改进狼群算法

3.1 双-头狼狼群算法

由于传统狼群算法迭代过程中狼群大都集中于头狼位置附近,算法求解容易陷入局部最优的情况[16]。为提高算法的寻优能力,笔者在求解目标分配的狼群算法基础上提出了双-头狼狼群算法(DLWPA:Double-Leader Wolf Pack Algorithm)。DLWPA在保留头狼机制的同时在狼群中增加了次头狼产生机制。在狼群算法中,头狼代表当前狼群中目标函数值最优的人工狼,故而设计出的次头狼代表当前狼群中目标函数值次优的人工狼。在加入次头狼产生机制后,算法从一次迭代得到一个最优解转变为一次迭代得到一个最优解和一个次优解[17]。

在DLWPA中,次头狼的存在意义是为了带领陷入局部最优的部分人工狼跳出局部最优循环,进而在解空间中继续搜索最优值。由于算法中存在两个解(即头狼和次头狼),狼群在搜索最优解的过程中会被要求分为两组分别在头狼和次头狼附近进行搜寻,从而增大对解空间的搜素范围。同时,由于两组狼群的人工狼个体在每次迭代中都为随机分配,原本跟随头狼的狼群会被次头狼所吸引,原本跟随次头狼的狼群也可能在下次迭代中被头狼所召唤,如此将会出现狼群在头狼和次头狼之间来回奔袭的情况,以此增大算法的搜索精度。图2为DLWPA召唤行为示意图。

由图2可以看出,次头狼的搜索范围比头狼搜索范围更广,同时次头狼机制能令徘徊在头狼附近的人工狼向更多的解空间位置搜寻,从而增大人工狼的寻优能力。由于重复利用了人工狼在头狼与次头狼之间来回奔袭,算法无需增加狼群数目即可保证在解空间中的搜寻精度,减少了代码运行的负担,保证了算法的高效性[18]。

图2 DLWPA召唤行为示意图Fig.2 DLWPA calling behavior diagram

DLWPA同时还对传统狼群算法的更新机制提出改进,加入了“野生狼”概念,即在淘汰部分人工狼之后,在补充的人工狼中有一部分狼不再继承头狼的部分编码位,而是在解空间中随机生成。随机生成的野生狼重新分配群组而加入狼群智能行为,以此提高算法的精度。

3.2 狼群算法改进策略

在DLWPA中,次头狼与头狼保持一定距离并且次头狼的目标函数值小于头狼的目标函数值,即d次-头＞3 dnear且F次＜F头。以下为次头狼产生规则和改进后的狼群行为机制。

3.2.1 次头狼产生规则

次头狼限定条件:

1)次头狼与头狼的曼哈顿距离大于判定距离dfar=3 dnear;

2)次头狼的目标函数值F次小于头狼的目标函数值F头。

在DLWPA中,所有满足上述条件的人工狼里目标函数值最大的人工狼为次头狼,下面根据算法迭代中人工狼的变换情况对次头狼和头狼的更新机制进行设计。假设人工狼i经过智能行为后其目标函数值为头狼的目标函数值为FL,次头狼的目标函数值为FS,人工狼与头狼的曼哈顿距离为di-L。头狼与次头狼更新机制如下。

3.2.2 改进后的召唤行为

将除头狼与次头狼外的所有人工狼视为猛狼。头狼与次头狼同时发出召唤指令,所有猛狼随机分配至两组:猛狼组A和猛狼组B。两组猛狼再分别向头狼与次头狼位置奔袭,即对猛狼位置Xi执行一次至多次召唤算子Φ(Xi,Rb,b)。

召唤行为限定条件如下。

1)猛狼组A与猛狼组B中的狼群数目相同,组A奔袭向头狼,组B奔袭向次头狼。每次算法迭代后两组猛狼重新随机分配。

2)猛狼组A的奔袭行为结束条件:

①猛狼与头狼的曼哈顿距离小于阈值距离dnear;

②猛狼的目标函数值大于头狼的目标函数值;

③猛狼与头狼的剩余步长小于b。

3)猛狼组B的奔袭行为结束条件:

④猛狼与次头狼的曼哈顿距离小于判定距离ds-near=dfar-dnear=2 dnear;

⑤猛狼的目标函数值大于次头狼的目标函数值;

⑥猛狼与次头狼的剩余步长小于b。

满足条件①、③、④、⑥的猛狼停止奔袭行为并留在原地等待下一步指令。满足条件②的A组猛狼根据头狼与次头狼更新机制对头狼位置进行更新,满足条件⑤的B组猛狼根据头狼与次头狼更新机制对次头狼位置进行更新。

3.2.3 改进后的狼群更新机制

3.3 基于DLWPA的目标分配问题求解流程

步骤1 初始化。在解空间中随机生成N匹人工狼,定义各参数值,包括游走次数T,各步长a、b、c,召唤阈值距离dnear,围攻阈值数量S,杀伤概率阈值P阈,更新比例因子U,更新编码因子V,淘汰比例因子Q。

步骤2 选取。计算各人工狼的目标函数值,依据头狼和次头狼的产生规则选取头狼与次头狼。

步骤3 游走。除头狼与次头狼外所有人工狼发起次数为T的游走行为。依据头狼与次头狼更新机制对所有时刻的狼群执行贪婪决策。直至所有狼群个体达到最大游走次数,游走行为结束。

步骤4 召唤。头狼与次头狼同时发起召唤行为。除头狼与次头狼以外的所有人工狼随机分配成等量的两组:猛狼A组与猛狼B组。A组向头狼位置以b步长发起奔袭,B组向次头狼位置以b步长发起奔袭。若触发了头狼或次头狼的更新机制,则针对头狼或次头狼的新位置重新发起召唤行为。当所有猛狼依据奔袭行为结束条件停留在原地后,召唤行为结束。

步骤5 围攻。A组以头狼位置为猎物位置发起围攻行为,B组以次头狼位置为猎物位置发起围攻行为。两组猛狼依据头狼与次头狼更新机制对位置进行更新。所有猛狼停留在原地后围攻行为结束。

步骤6 更新。依据改进后的狼群更新机制对狼群进行更新。

步骤7 判断。当更新结束后,若头狼的目标函数值达到优化精度要求或迭代次数用尽,则输出此时头狼位置,否则转至步骤2。

综上所述,图3为DLWPA的目标分配流程图。

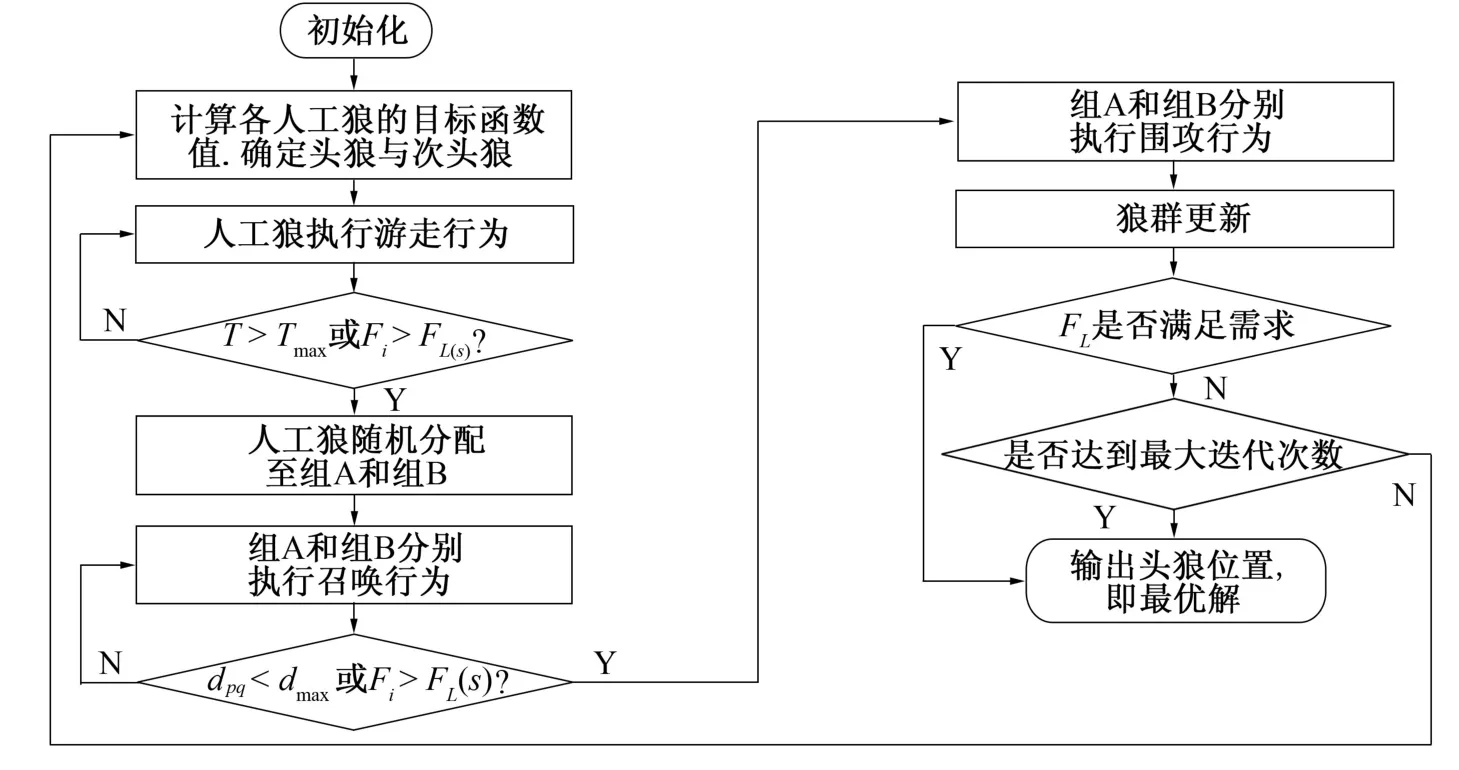
图3 基于DLWPA的目标分配流程图Fig.3 Flow chart of target allocation based on DLWPA

4 空战仿真实例研究及结果分析

笔者在Matlab软件的基础上[19],以空战8V16、10V14的战场态势为实验对照组,以所采用的智能寻优算法和各行为步长数值为变量参数,利用控制变量法通过仿真对照实验验证DLWPA的可行性与有效性。

针对8V16的空战战场,可假设整体战场态势如图4所示,我方为下方8架战机,飞行方向朝上;敌方为上方16架战机,飞行方向朝下。双方距离均处于导弹发射射程范围之内,根据前期战场态势评估结果可求出针对敌方各单位目标的价值收益函数矩阵为W1=[0.75 0.60 0.75 0.85 0.65 0.75 0.90 0.85 0.90 0.85 0.90 0.65 0.75 0.80 0.60 0.75]。同理,针对10V14的空战战场,假设整体战场态势如图5所示,可求得针对敌方各单位目标的价值收益函数矩阵为W2=[0.80 0.70 0.60 0.85 0.90 0.75 0.85 0.95 0.70 0.70 0.75 0.60 0.65 0.75]。我方各战机对敌方各目标的杀伤概率矩阵分别为实验数据如表1所示,笔者分别采用WPA算法和DLWPA算法对目标分配问题进行优化求解,设定初始参数人工狼总数N=20,最大迭代次数为200,杀伤概率阈值P阈=0.80,最大游走次数T=8,召唤行为阈值距离dnear=6,围攻行为阈值数量S=2,更新比例因子U=2,更新编码因子V=4,而且探究了各行为步长数值对算法精度和效率的影响,实验结果如表2、表3所示。表1中平均耗时指算法代码运行100次后解算出的平均耗时,最优结果次数指算法代码运行100次所得最优结果的数量。

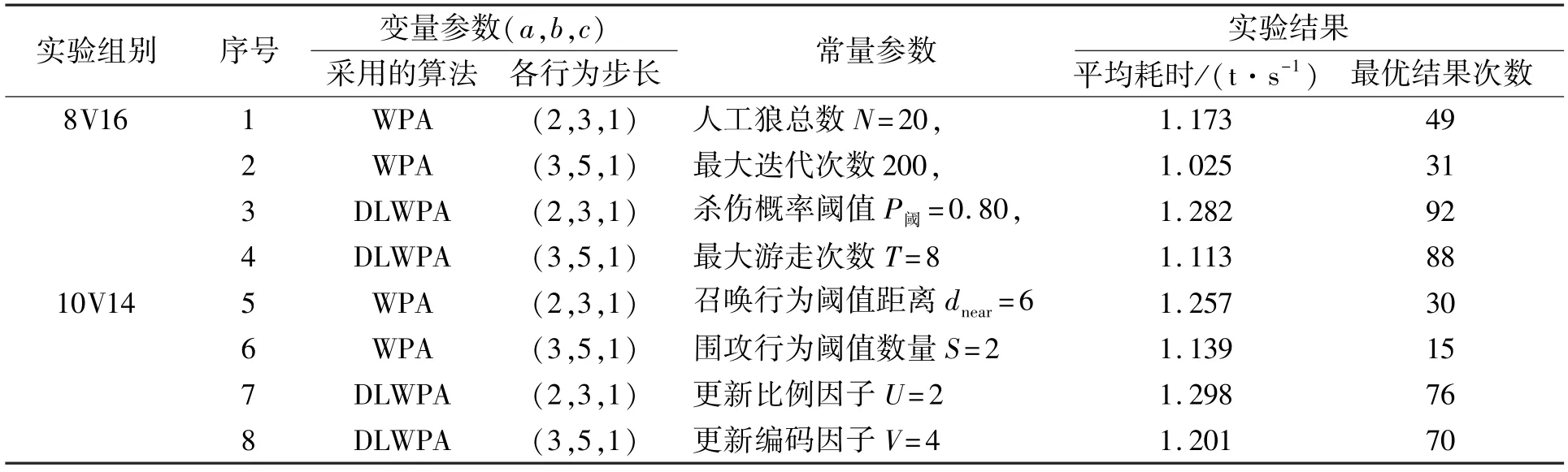
表1 仿真对照实验数据对照表Tab.1 Experiment data of simulation comparison

表2 8V16战场模型仿真实验数据结果表Tab.2 Experiment data of 8V16 battlefield model simulation

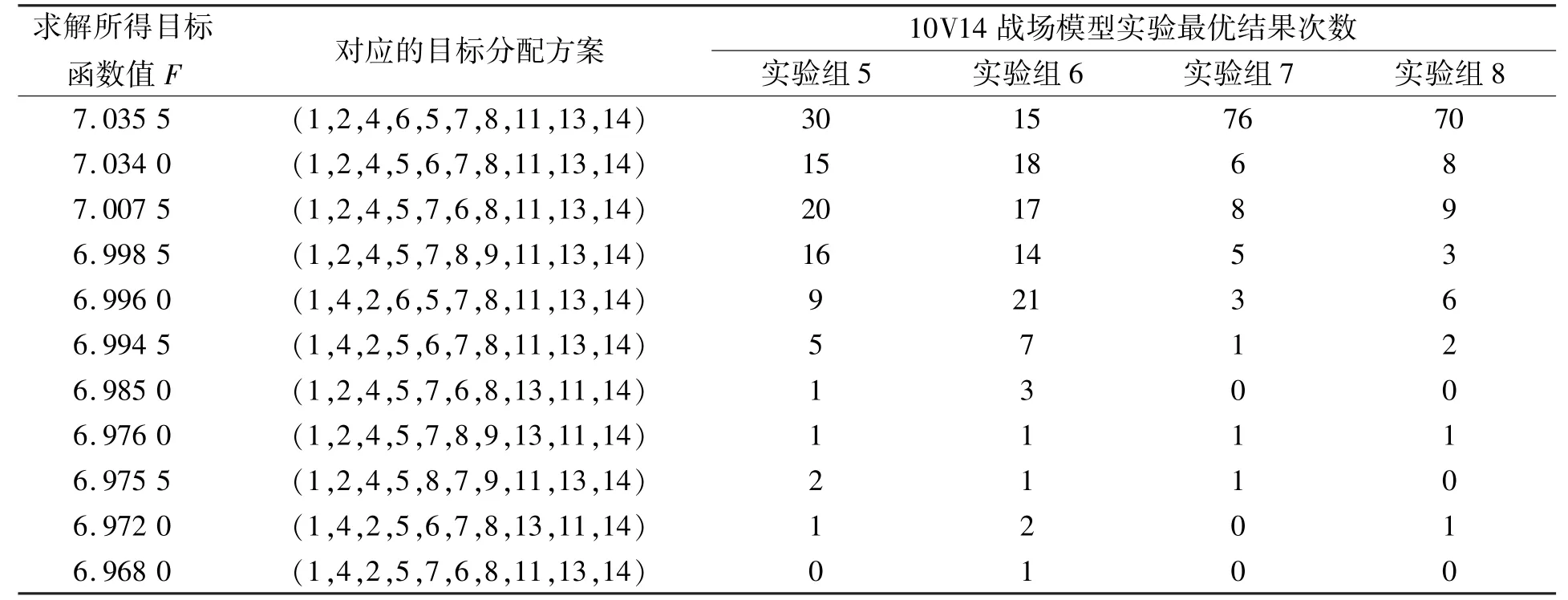
表3 10V14战场模型仿真实验数据结果Tab.3 Experiment data of 10V14 battlefield model simulation

图4 8V16战场模型态势示意图Fig.4 Schematic diagram of the 8V16 battlefield model situation

图5 10V12战场模型态势示意图Fig.5 Schematic diagram of the 10V12 battlefield model situation

由实验结果可分析出,采用DLWPA求解当前战场态势环境下的目标分配问题具有良好的寻优效果。对比实验组1和3、实验组2和4可知,在相同的一定条件下,DLWPA算法对问题求解的精度有显著的提升。这说明算法改进后其全局搜索能力有所提高,且陷入局部最优的情况更少说明此时算法具有一定的跳出局部最优情况的能力。当战场模型转换成10V14的模型时,DLWPA算法依然保持着高精度的优势,这证明该算法在一定程度上具有良好的适用性,能针对多种不同的空战场景。对比实验组1和2、实验组3和4可知,算法各行为的步长较小时,算法精度较高,局部搜索能力更强。但较小的步长会令算法迭代次数增多,增加了算法的耗时,故而在选取各行为机制的步长时,应该根据实际需求选取合适的步长。对比两个战场模型中步长变化的对照实验组,可以发现步长导致的变化对DLWPA算法影响较小,对WPA算法影响较大。这是因为DLWPA本身已具备较为良好的求解精度,调节步长数值带来的效益对于DLWPA更小。因此,笔者提出的DLWPA对传统狼群算法做出了改进并能有效提高其对全局最优解的寻优能力。

5 结 语

笔者针对空战目标火力分配问题进行了研究,在传统狼群算法的基础上提出了一种改进策略。从空战态势模型入手,描述目标火力分配问题,通过引入“次头狼”概念改进狼群算法,从而使算法具备更好的寻优能力。通过仿真实验可以看出,改进后的算法很好地改善了狼群易陷入局部最优的情况,一定程度上弥补了狼群算法的不足,具有很大的实用价值,为研究多机对抗目标分配问题提供了一种新的解决方案。今后研究的方向将放在提高算法的寻优速度上,目前算法上猛狼分组的行为机制使DLWPA在寻优速度上无法做出很好的改进。探究如何在保证高精度的同时,提高算法的寻优速度将成为今后研究的重点。