经典Canny 边缘检测的量子实现

鲍华良赵 娅

(东北石油大学 计算机与信息技术学院,黑龙江 大庆163318)

0 引 言

量子图像处理是量子计算和图像处理的新兴交叉学科,2003年,Beach等[1]首次报道了有关量子图像处理的研究。进行量子图像处理的第1步是将经典图像用量子方法表示。早期提出的两个转换模型是量子比特晶格表示法[2]和实矢量表示法[3]。尽管这两种表示法都有一些缺陷,但它们为后续研究奠定了基础。量子图像处理的快速发展得益于2011年Le等[4]提出的FRQI(Flexible Representation of Quantum Images)表示法,该模型首次使用量子叠加态存储像素的位置。之后提出的表示模型都是其基本模型的修改或扩展,如SQR(Simple Quantum Representation)[5]、MCQI(Multi-Channel Quantum Images)[6-7]等。2013年,Zhang等[8]提出了新型的数字图像增强量子表示法(NEQR:Novel Enhanced Quantum Representation),这种表示方法的优点是,通过有限次数的投影测量,可以精确地检索出像素的颜色信息。

目前,量子图像处理已经开展的工作主要包括:图像置乱[9-10]、图像加密[11]、图像水印[12-13]、图像隐写[14]、量子电影[15]、量子音频[16]、图像匹配[17-18]、图像分割[19-23]、几何变换[20]、颜色处理[21]、特征提取[22]、图像定位[24]和边缘检测[25-26]。经典图像处理中,边缘检测涉及卷积或相关计算,而使用量子线路实现这些计算是相对困难的。Fan等[27-28]提出了基于Laplacian算子和零交叉方法的量子图像边缘提取,同时提出了基于经典Sobel算子的NEQR的量子图像边缘提取。文献[27-28]作为量子边缘检测的先驱,对未来的研究具有指导意义。

综上所述,量子图像处理经过十多年的发展,已经取得了许多原创性的成果,但仍面临许多挑战[29]。例如,在经典图像处理中,边缘检测方法非常完备,但对量子图像处理还不成熟。笔者研究了基于量子计算的Canny边缘检测的实现方案,设计了完整的量子线路。借助量子计算的并行性,该方案可以实现对应经典方案的指数加速,经典计算机上的仿真验证了方案的正确性。

1 预备知识

1.1 经典Canny边缘检测

令f(x,y)表示输入图像,G(x,y)=e-(x2+y2)/(2σ2)是高斯滤波函数。Canny边缘检测算法包括如下步骤。

Step 1 用高斯滤波器平滑输入图像得到fs(x,y)。

Step 2 采用Sobel算子计算梯度的幅值图像和角度图像

Step 3 对梯度幅值图像应用非最大抑制。

对以α(x,y)中每个(x,y)为中心的3×3区域,应用Rafael等[30]提出的非最大值抑制方案:首先找出最接近α(x,y)的方向dk。若M(x,y)沿dk方向大于其邻近的两个像素值,则令gN(x,y)=M(x,y),否则gN(x,y)=0,此时gN(x,y)即为非最大抑制图像。

Step 4 采用双阈值处理检测并连接边缘。

Canny算法通过使用两个阈值改进该状况。设置高阈值为TH,低阈值为TL。通常高阈值和低阈值的比率可取为2 ∶1或3 ∶1。双阈值处理操作视为

两幅阈值图像的叠加。起始gNH(x,y)和gNL(x,y)都被置为零,但由于gNL(x,y)是使用低阈值形成的,故在阈值处理后gNH(x,y)的非零像素通常少于gNL(x,y),且gNL(x,y)中包含着gNH(x,y)中所有非零的像素。通过令

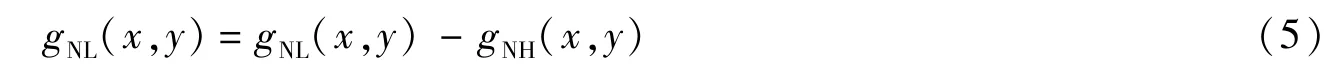
从gNL(x,y)中删除所有来自gNH(x,y)的非零像素点。gNH(x,y)中的边缘通常会存在缝隙,可使用文献[26]中的方法形成较长的边缘。最后,将gNL(x,y)中所有的非零像素附加到gNH(x,y)中,此时即可得到Canny边缘检测图像。

1.2 NEQR模型

考虑到Canny边缘检测涉及大量的灰度值计算,所以采用NEQR模型表示量子图像。对一幅2n×2n且颜色值范围均为{0,1,…,2q-1}的灰度图像,NEQR可描述为

1.3 补码定义

在Canny边缘检测中,由于梯度值可能为负数,为方便计算,像素的灰度值统一用二进制补码表示,为此首先给出二进制补码的定义。

设x为一个n+1位的二进制数,包括1个符号位(0表示“+”,1表示“-”),m个整数位,以及n-m个小数位。x的补码

获得。在后面设计的各种模块中,所有与像素的灰度值有关的数据都将用二进制补码表示。

1.4 量子比较器

量子比较器的设计方法可参见文献[27],为便于描述,采用图2 a给出的模块符号图表示,其中x和y是两个n比特输入数,e1e0是输出比特。若e1e0=10,则x＞y;若e1e0=01,则x＜y;若e1e0=00,则x=y。

1.5 模加1和模减1

对n位无符号整数x,这两个模块分别实现模加1和模减1。对n+1位有符号数,这两个模块分别实现x+2m-nmod 2m和x-2m-nmod 2m。两模块的符号如图2 b、图2 c所示,具体量子线路设计参见文献[22]。

图2 比较器、模加1和模减1量子线路的模块符号Fig.2 Module symbols of quantum circuits of comparator,modulo plus 1 and minus 1

2 量子Canny边缘检测的线路设计

2.1 一些辅助模块的量子线路

1)复制模块。该模块的功能是将一个n比特量子态复制到另一个n比特量子态显然可以用n个受控非门实现。具体的量子电线如图3所示。在该模块的符号中,不变的输入和输出用实心条标注。

图3 复制模块量子线路图Fig.3 The quantum circuit of copy module

2)翻转加1模块。该模块计算n+1位有符号数的相反数。设x=xm,xm-1…x0.x-1…xm-n为n+1位有符号数,该模块首先对x中的所有量子比特进行翻转,然后对翻转后的量子比特实施模加1,量子线路如图4所示。

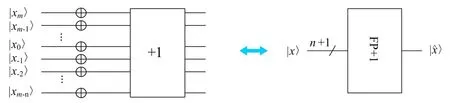
图4 翻转加1模块量子线路图Fig.4 The quantum circuit of flip and plus 1

3)左移和右移模块。左移模块将有符数x=xm,xm-1…x0.x-1…xm-n依次向左移动1个比特位,并将最低有效位置为0,如下所示

该模块也称加倍模块。其具体的量子线路如图5所示。该模块将在设计补码除法器中发挥重要作用。

图5 左移模块量子线路图Fig.5 The quantum circuit of left shift module

右移模块将有符数x=xm,xm-1…x0.x-1…xm-n依次向右移动1个比特位,使其成为n+2位的有符号数。由

可知,右移模块将数值减半,其量子线路如图6所示。

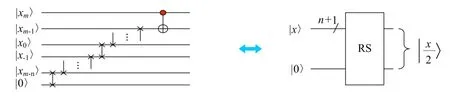
图6 右移模块量子线路图Fig.6 The quantum circuit of right shift module

4)绝对值模块。该模块计算有符号数x=xm,xm-1…x0.x-1…xm-n的绝对值,其量子线路如图7所示。

图7 绝对值模块量子线路图Fig.7 The quantum circuit of absolute value

5)模加法器模块。加法包括模加法和非模加法,如果加法的结果小于模,则这两种加法是等价的。对两个n+1位有符号数的加法,如果结果超过模,则通过使用n+2位表示这两个数,这两个加法仍然是等价的。设两个有符号数分别为x=xm,xm-1…x0.x-1…xm-n,y=ym,ym-1…y0.y-1…ym-n,且2m-1。模加法器的量子线路图如图8所示。

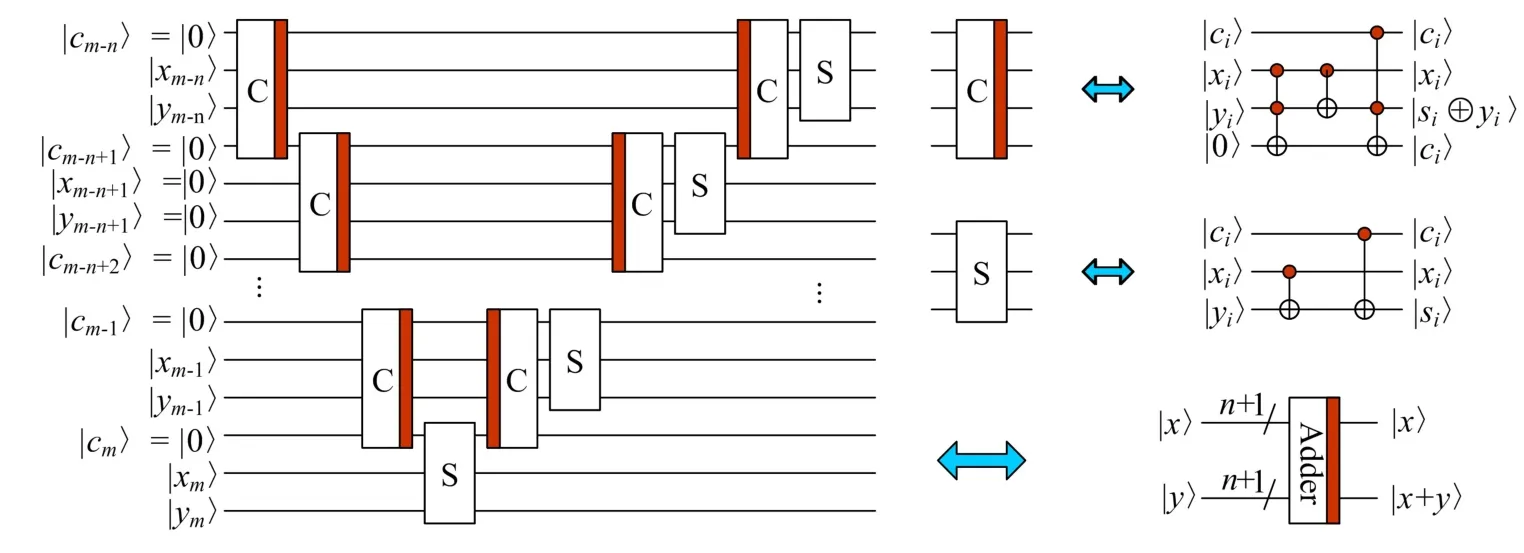
图8 量子模加法器模块量子线路图Fig.8 The quantum circuits of modulo adder

6)补码比较器模块。图2a中的比较器只能比较两个无符号整数,对两个n+1位有符号数的比较,可使用图9所示的补码比较器实现。

图9 补码比较器模块量子线路图Fig.9 The quantum circuit of complement comparator

7)补码乘法器模块。设x=xm,xm-1…x0.x-1…xm-n,y=ym,ym-1…y0.y-1…ym-n为2个n+1位有符号数的补码,实现x×y的量子线路如图10所示。在这个线路中,乘积采用2n+1个比特描述,包括1个符号位、2m个整数位和2(n-m)个小数位。

图1 一个平滑图像fs的3×3区域和Sobel算子Fig.1 A 3×3 region of smoothed image fs and two Sobel operaters in X and Y directions

图10 两个有符号数补码乘法器的量子线路图Fig.10 The quantum circuit of complement multiplier for two signed numbers

此时,两个任意有符号数x和y的商可由

计算。显然式(11)涉及指数计算,p是m+1位有符号数的补码表示,其中p=pm,pm-1…p0,需要解决在x和p都已知的情况下计算2p x,实现此功能的量子线路如图13所示。

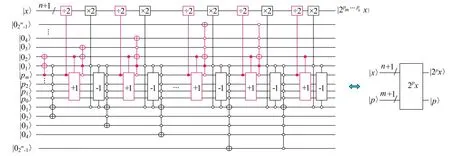
图13 已知x,p计算2p x的量子线路图Fig.13 The quantum circuit for caculating 2p x based on known x and p

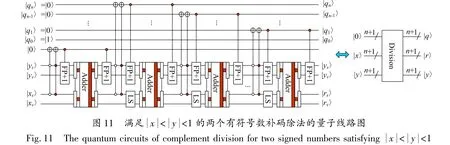
综上所述,笔者设计的任意两个有符号数的补码除法器的量子线路如图14所示。该模块将用于量子Canny边缘检测的梯度角度图像。

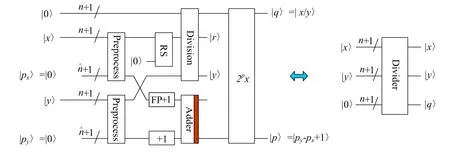
图14 实现任意两个有符号数补码除法的量子线路图Fig.14 The quantum circuit of complement division for any two signed numbers

2.2 实现Canny边缘检测的量子线路

1)原始图像的高斯滤波。为避免卷积运算,采用移位、堆叠、加权求和的方法实现输入图像的高斯滤波。先将原始图像在8个方向(即上左、上、上右、左、右、下左、下、下右)移位一个单位或多个单位(取决于滤波器模板的大小)。然后将移位后的图像和原始图像按照固定的顺序进行堆叠。在这些堆叠的图像中,相同位置的像素就是原始图像中被滤波器模板覆盖的像素。最后,以滤波器模板中的对应的值为权重,计算这些位置相同的像素的加权和就是原始图像中相应像素的滤波结果。这种方法的优点是,借助量子计算的并行性,可以同时处理叠加图像中相同位置的所有像素。

实现高斯滤波的第1步是确定滤波器的大小。笔者采用文献[28]提出的方法,即滤波模板边长S通常取大于6σ的最小的正奇数,其中σ为输入图像短边长度的0.5%。本文中,当输入图像的短边长度小于300时,采用上述方法确定S,否则,取S=9,σ=1.5。在确定高斯滤波器的大小后,通过对高斯函数进行采样,可得到高斯滤波器模板。以128×128像素的输入图像为例,σ=0.64,「6σ]=4,S=5,此时采样得到的高斯滤波器模板如图15a所示。设输入图像为Ixy,根据移位、堆叠、加权求和,此时,需要生成24幅移位图像,如图15b所示。

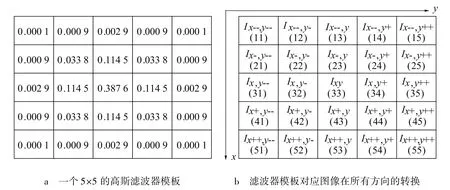
图15 一个5×5的高斯滤波器模板和对应输入图像在所有方向上的转换Fig.15 A 5×5 Gaussian filtering mask and its corresponding input image translation in all directions

笔者以3×3的滤波器模板为例,设计了实现高斯滤波的量子线路,如图16所示。其中像素的输入图像,灰度值由n+1位有符号数的二进制补码表示,包括一个符号比特和n个数据比特,整个线路可分为3部分。

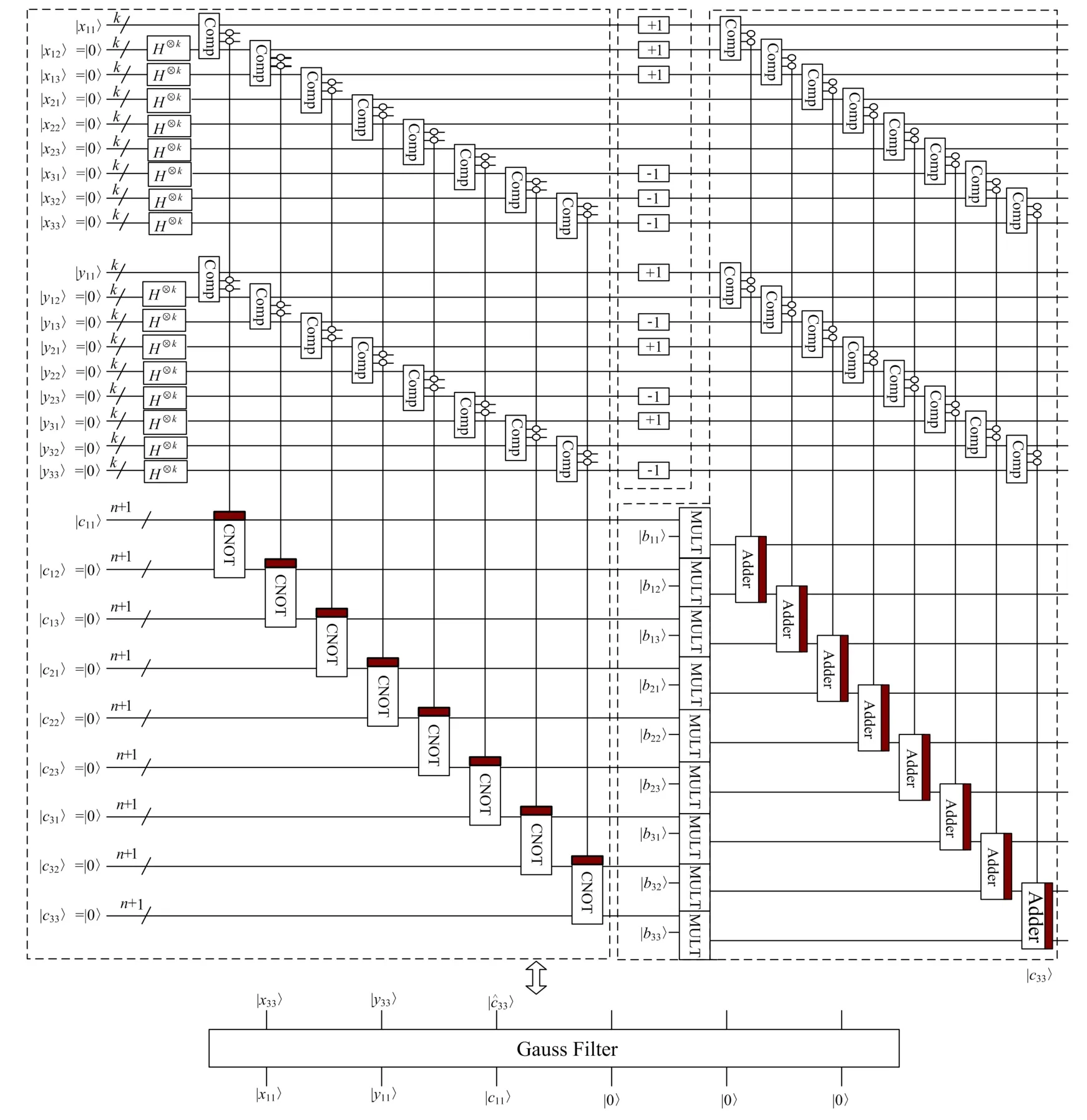
图16 高斯滤波量子线路图Fig.16 The quantum circuit of Gaussian filtering

第1部分如第1个虚线框中的线路所示,用于生成与输入图像完全相同的8幅空图像。然后利用若干比较器和复制模块将输入图像的灰度值复制给这8幅空图像。第2部分如第2个虚线框中的线路所示,用于获得向各方向的平移图像。第3部分如第3个虚线框中的线路所示,用于计算堆叠图像中相同位置的加权和,即滤波结果。为使计算结果尽可能精确,对所有结果保留小数点后4位,即精确到

0.000 1,由2-14＜10-4,二进制小数需要用14个量子位表示,灰度范围0~255需要用8个量子位表示,因此总共需要1+8+14=23量子位。

为获得梯度幅值图像和角度图像,需要利用式(1)和式(2)计算经过Sobel算子处理后输出的梯度幅值和角度。为简化量子线路设计,利用

代替式(1)和式(2)。式(12),式(13)利用绝对值代替平方和开方运算,使用正切值代替角度值。这种简化有效避免了复杂的量子线路设计。后续的实验结果表明这种简化对边缘检测的结果没有影响。

简化公式只涉及加法和除法运算,从而简化了量子线路设计,只需比较gx和gy的像素位置,当位置相同时,进行两个像素值的加法和除法,并将计算结果复制到空图像中相同位置的灰度值。具体量子线路图如图18所示分别是梯度幅值图像和梯度角度正切值图像。

图18 计算梯度幅值和角度正切值的量子线路图Fig.18 The quantum circuit of computing gradient magnitude and tangent of gradient angle

3)对梯度幅值图像的非最大抑制。与经典的Canny边缘检测类似,对梯度幅值图像的非最大抑制要分别在4个方向上实现,因此需要预先确定4个方向上的梯度角度的正切值的范围。通过对单位圆8等分可知,水平、垂直、+45°、-45°的4个方向的正切值范围如下

其中t1=-0.414 2,t2=0.414 2,t3=2.414 2,t4=-2.414 2。实现水平方向非最大抑制的量子线路如图19所示,其他方向的量子线路设计与之类似,不再赘述。

图19 水平方向非最大抑制的量子线路图Fig.19 The quantum circuit for non-maxima suppression in horizontal direction

图19中黑色虚线右侧的线路使用绝对值模块和量子比较器模块判断正切值是否满足水平边缘的条件。若当前正切值满足水平边缘条件,且满足条件Mag(p)＞max(I12(p),I32(p)),则将Mag(p)的结果存储到的当前位置。

4)基于双阈值的边缘细化和连接。

图21 Canny边缘检测的量子线路的总体框架图Fig.21 The general framework of quantum circuit for Canny edge detection

相比文献[26]中的Canny边缘检测量子实现,笔者使用的滤波器模板大小不是固定的,而是随输入图像大小自适应变化,且滤波器模板中的数值是经典连续滤波函数的采样结果,这样的设计与经典Canny边缘检测的效果更为接近。

2.3 复杂度分析

为便于描述,以一个2k×2k像素的灰度图像(共2 k+23个比特)为例,分析模型的线路复杂度。在量子图像处理中,模型复杂度取决于线路中基本门(大小为2×2的酉算子)数量,且基本门的复杂度默认为1[32]。下面通过分析各子模块的复杂度,逐步得出整个模型的线路复杂度。

从文献[31]可知,模加1和模减1模块、比较器模块的复杂度都不超过O(k2)。从图3~图5可知,复制模块由n个受控非门组成,因此复杂度为O(n)。翻转加1模块由n个非门和1个模加1模块组成,因此复杂度是O(n2+n)≈O(n2)。左移模块由n个交换门和两个受控非门组成。每个交换门可以分解为3个受控非门,所以电路的复杂度为O(3 n+2)≈O(n)。同理,右移模块的复杂度也是O(n)。

从图7和图8可知,绝对值模块由一个受控非门和一个翻转加1模块组成,因此复杂度约为O(n2+1)≈O(n2)。模加法器包括2 n个进位模块和n+1个求和模块。每个进位模块由2个Toffoli门和1个受控非门组成,每个求和模块由2个受控非门组成。根据文献[32],1个Toffoli门可以近似为6个受控非门,因此模加法器的复杂度为O(28 n+2)≈O(n)。

根据图9和图10可知,补码比较器模块由1个模加法器、1个翻转加1模块、1个非门和1个受控非门组成。因此,复杂度不超过O(n2+n+2)≈O(n2)。补码乘法器由2(n+1)个模加法器、2 n+1个翻转加1模块以及n个右移模块组成,补码乘法器的复杂度为O((2 n+1)n+(2 n+1)n2+n2),即O(n3)。

由图11~图13可知,补码除法器包括预处理、除法器、2px等模块。如图12所示,预处理模块由翻转加1、左移模块、右移模块、模加1和模减1模块组成,其复杂度不超过O(k2+n2)。由文献[33]和文献[34]可知,除法器的复杂度不超过O(n3)。2px模块由左移,右移、模加1、模减1模块组成,其复杂度不超过O(k2+n)。所以补码除法器的复杂度不超过O(k2+n3)。对大小为S×S的高斯滤波器模板,线路包含2(S2-1)k个Hadamard门、4(S2-1)个比较器,0.5(S3-S)个模加1和模减1模块、S2-1个复制模块、S2-1个补码乘法器和S2-1个模加法器。因此,高斯滤波器线路的复杂度过O(k2)。

图12 对有符号数x进行预处理的量子线路图Fig.12 The quantum circuit of preprocessing for a signed number x

根据图17可知,Sobel-X和Sobel-Y由比较、复制、左移、模加1模减1、翻转加1、模加法器组成。因此,它们的复杂度不超过O(k2+n2)。梯度幅值模块由比较器、复制、补码比较器和模加法器组成,因此复杂度不超过O(k2+n3)。梯度角度模块主要由比较器和量子除法器组成。因此其复杂度不超过O(k2+n3)。从图19和图20可知,非极大抑制模块主要包括比较器、复制、量子比较器模块。因此,复杂度不超过O(k2+n2)。双阈值模块主要由比较器、复制模块、补码比较器、模加1和模减1以及模加法器模块组成。因此,复杂度不超过O(k2+n2)。

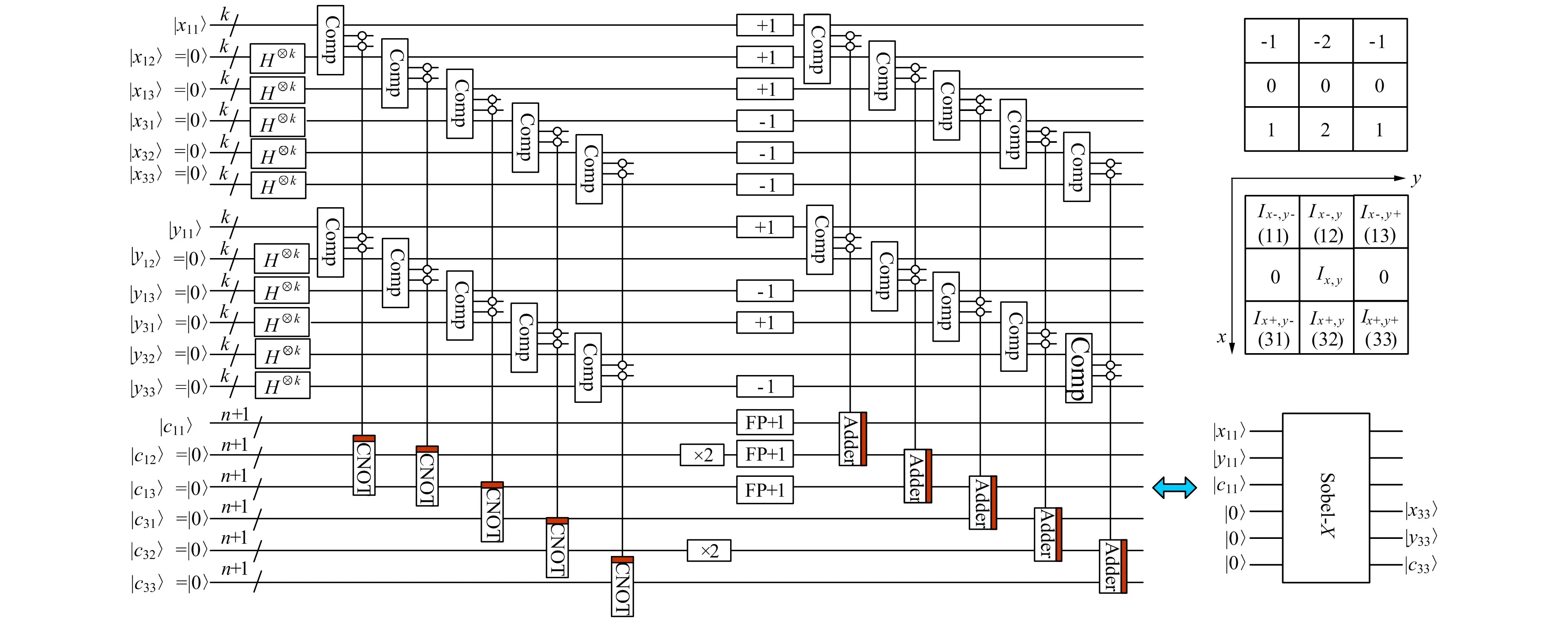
图17 Sobel-X算子及对应的量子线路图Fig.17 Sobel-X mask and its quantum circuit

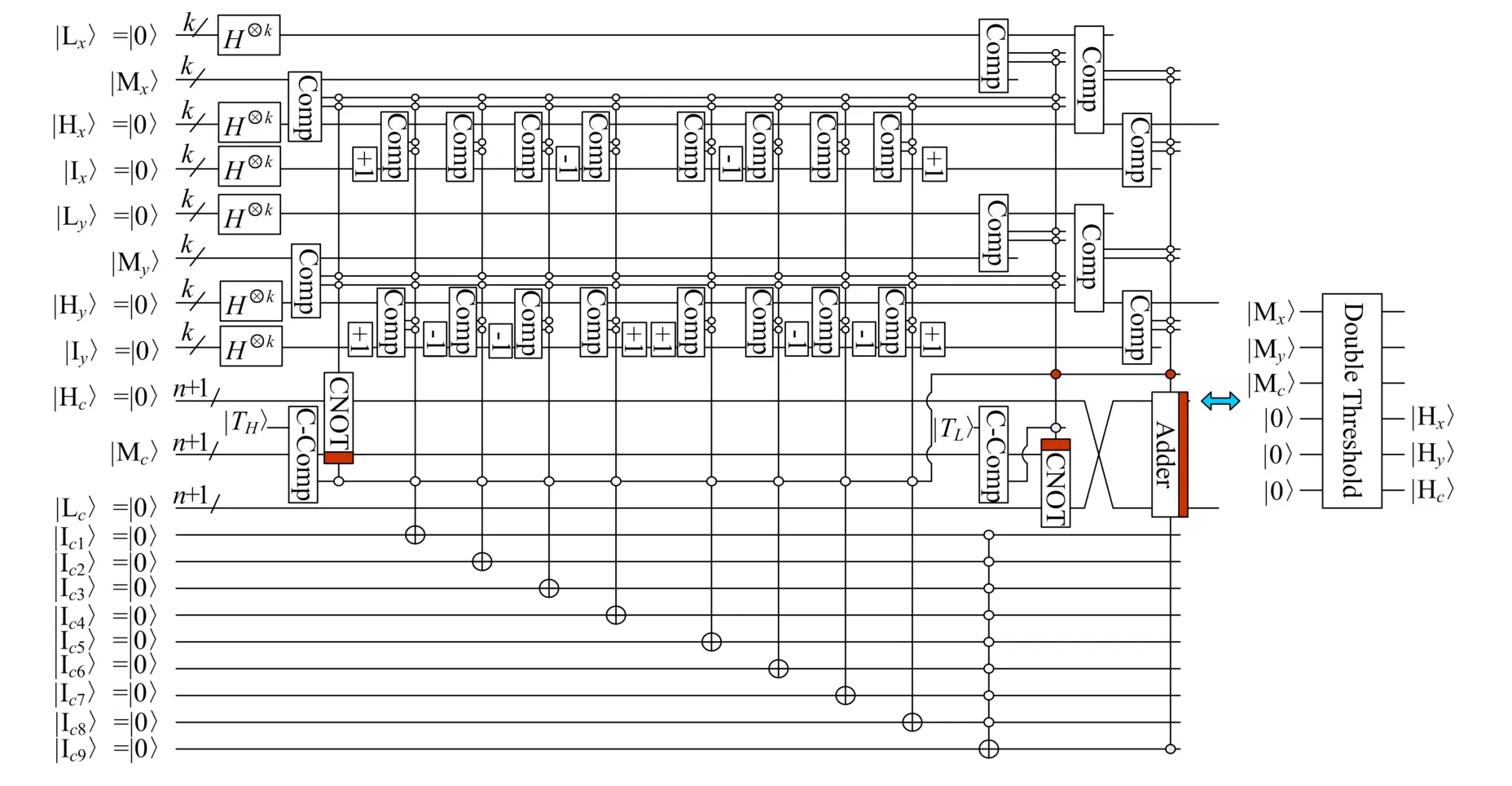
图20 基于双阈值的边缘细化和连接的量子线路图Fig.20 The quantum circuit for edge refinement and linking based on double threshold

综上所述,笔者设计的边缘检测方案的复杂度为O(k2+8(k2+n2)+(k2+n3))≈O(k2+n3)。

3 仿真结果及分析

由于目前量子计算机的硬件实现尚处于理论探索阶段,所以仿真只能在经典计算机上进行。虽然不能验证量子计算的并行性,但能验证方案的执行效果。所有仿真在配置为英特尔(R)Core(TM)i7-10700CPU@2.90 GHz、8.00 GByte内存和64位操作系统的台式机上进行,软件采用Matlab(R2014b)。仿真实验中用向量表示图像,用矩阵表示算子,使用的4幅灰度图像如图22所示。第1幅为233×233像素,接下来两幅为512×512像素,最后一幅为1 024×1 024像素。值得指出的是,图像均采用NEQR模型表示,图像大小必须满足2n×2n像素。为使第1幅图像满足此要求,分别在图像底部和右侧增加23行和23列,将图像扩展为256×256像素,并将新增加的像素值全部设置为零。

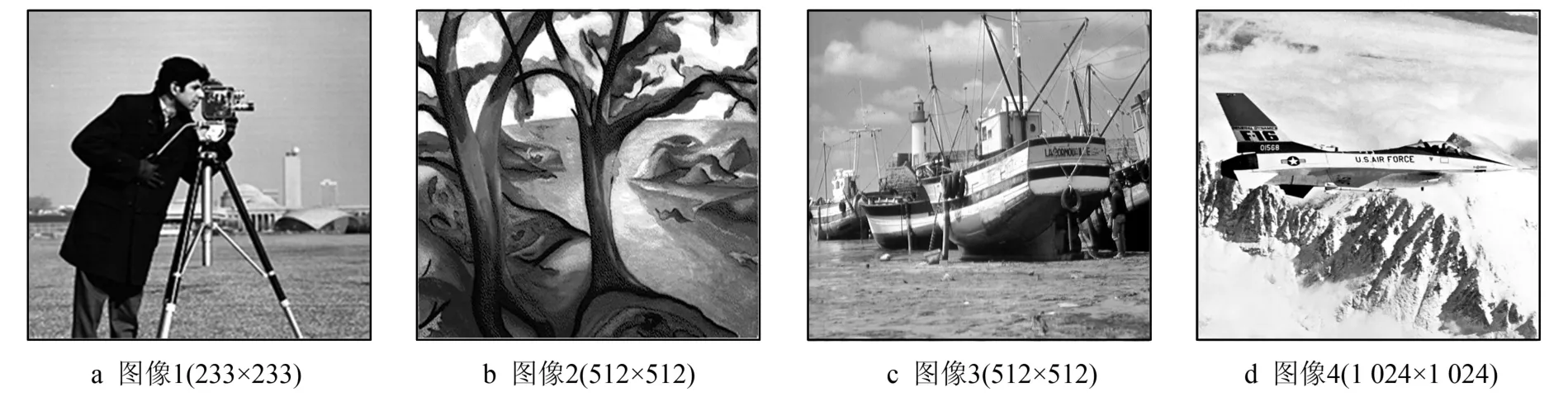
图22 实验中采用的4幅原始图像Fig.22 Four original images used in the experiment

对第1幅233×233像素的图像,高斯函数的标准差σ=233×0.5%=1.650,高斯滤波器模板的边缘长度为S=「6σ]=7。对后两张图像,因为图像的边缘长度大于300,所以σ=1.5,S=9。两个滤波器模板中每个元素的具体数值分别如图23a,图23b所示。

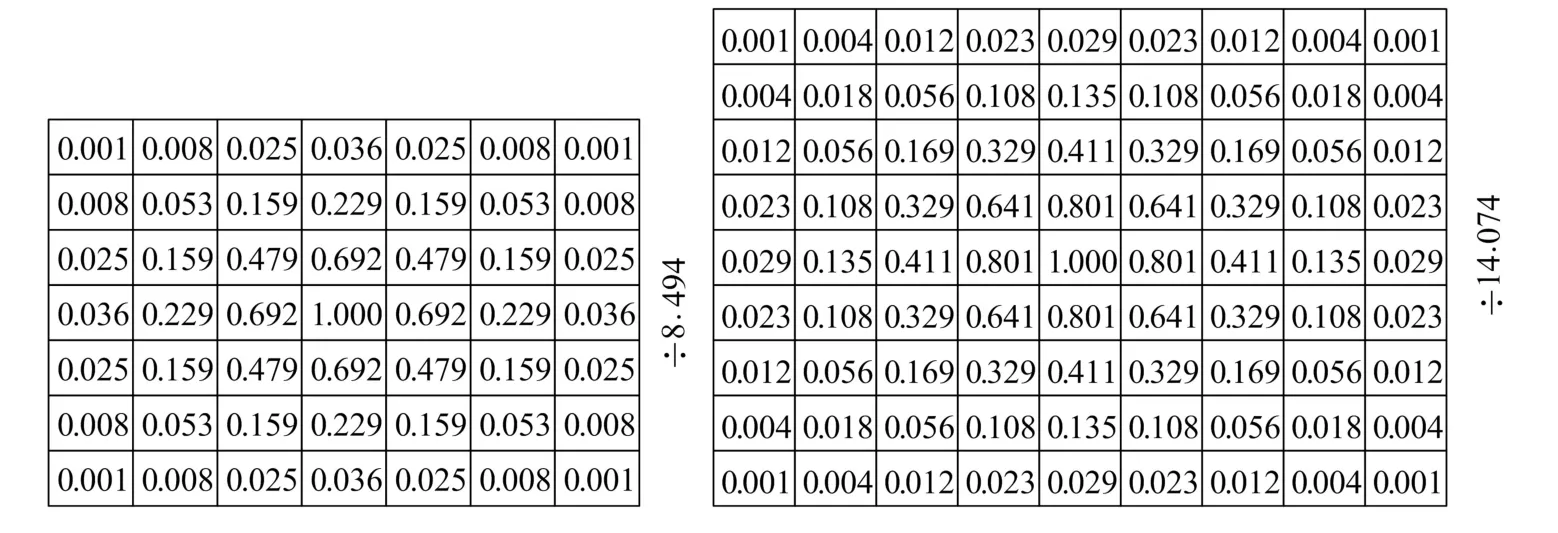
图23 实验中使用的两个高斯滤波器模板Fig.23 Two Gaussian filtering masks in the experiment

为突出量子Canny边缘检测方案的处理效果,将其结果与经典的Canny边缘检测结果进行了比较。在双阈值处理中,高阈值和低阈值分别取梯度最大值的30%和10%。量子Canny边缘检测的效果和经典Canny边缘检测的效果如图24a,图24b所示。

图24 两种检测方案的实际效果比较Fig.24 Comparison of the actual effects of two edge detection schemes

上述经典计算机实验不能模拟量子计算的并行性,仿真结果与用量子计算机实验不完全一致,但可大致模拟量子边缘检测的执行结果。从两种边缘检测的结果可以看出,量子方案略优于经典方案。从图24可以看出,量子边缘检测方法检测到的边缘更薄而且边缘周围的区域更加清晰。而经典方案检测到的边缘更加粗糙,且在边缘内部还有一些模糊区域。

该实验中量子Canny边缘检测比经典的Canny边缘检测效果略胜一筹,是因为该实验中高斯滤波使用了不同的滤波器模板。经典方案是基于固定的5×5的高斯滤波器模板,而量子方案使用的滤波大小随输入的图像大小而改变。此外,两种方案的滤波器模板的值也不同,在本实验模拟经典方案时,滤波器模板中的所有数据都是整数,并不是用高斯函数直接采样的结果。而量子方案中的滤波器模板的数据则是通过高斯函数直接采样的结果。

另外,尽管在经典方法中,也可以采用不同大小的滤波器模板,而且滤波器的具体数值也可以采样于高斯连续函数,但两种方案对图像边界像素的处理方式是不同的。在经典方案中,当滤波器移动到边界时,对边界之外的像素,其像素值一般按0值处理,或采用将边界像素复制外推的方式处理;在该方案中,所有边界像素实际上都是采用循环移位的方式处理的,这种方式显然比经典方式中的0值处理方式优越。

值得指出,稍好的检测效果并不是本方案的核心优势,量子边缘检测方案的核心优势在于计算效率的大幅度提升。对一个2n×2n像素的图像,经典方案必须逐个像素执行,复杂度必然含有因子2n,而本方法利用量子计算的并行性可对所有像素同时执行滤波操作,在一定程度上实现了经典方案的指数加速,这是量子方案相较于经典方案的核心优势。

4 结 语

边缘检测是图像处理和计算机视觉中的一个基本问题,目的在于识别数字图像中亮度变化显著的点。在经典的方法中,Canny边缘检测的高斯滤波可以通过卷积实现。笔者使用移位、堆叠、加权求和的方法避免了卷积运算,该方法为设计量子图像滤波提供了可行性。笔者设计了经典Canny边缘检测的量子版本,从基本的模块设计入手,给出了完整的Canny边缘检测的完整量子线路。经典计算机上的仿真实验验证了所提方案的有效性。就边缘检测的效果而言,量子Canny边缘检测的性能略优于经典Canny边缘检测,但该方案的突出优势在于它的计算效率,分析表明该方案可以实现对经典方案的指数加速。