风力发电机定子振动测试及响应分析
2022-01-13曹国豪马武福
李 源,曹国豪,马武福,梁 臣,胡 鑫
东方电气风电有限公司,四川 德阳 618000
引言
在生态环境日益恶化和化石能源逐渐枯竭的今天,风能作为一种可再生的清洁能源越来越受到世界各国的重视[1-5]。为了更有效地获取风能,风力发电机组单机容量也逐渐增大,同时,直驱式机组省去了齿轮箱等部件,大大降低了运行维护成本,提高了机组整体可靠性。因此,大容量直驱式风力发电机组得到了迅速发展[6-9]。
发电机作为直驱式风力发电机组的关键部件之一,振动会加速轴承的磨损,提高机组的噪声,降低整机的输出性能[10-13],因此,限制发电机振动效应对整个机组的正常运行有着重要意义。在许多情况下,发电机的振动除了与气隙磁场产生的磁力有关外,还取决于发电机的共振频率,与机械固有频率有很大关系[14-18]。黄礼文[19]使用传递函数的模态分析法对发电机定子铁芯的振动模态进行了研究。周盛强等[20]在振动模态有限元分析的基础上,引入模态选择方法,仿真计算了超声电机定子的机械和电学响应。覃万健等[21]对永磁电机的定子进行模态实验和有限元模态分析,将实验数据与仿真数据进行了比较分析。黄克峰等[22]使用机电类比的方法推导了永磁同步电机固有频率的计算方法,并使用有限元软件对定子进行模态分析。韩伟等[23]考虑了各个结构对其定子固有频率的影响,使用有限元软件准确计算了异步电机的固有频率,并系统性分析了三维振动模态。龙英睿等[24]使用有限元分析和模态分析理论对风力发电机定子支架的固有频率和模态振型进行了研究。关于风力发电机定子的振动研究集中在固有频率的计算和模态分析等方面,对发电机定子机架的响应分析研究较少,同时,缺少风力发电机在运行过程中定子部件振动情况的测试。因此,有必要对风力发电机定子的振动情况进行实际测试和仿真。
本文以某永磁直驱风力发电机组为研究对象,对其风力发电机定子的振动加速度进行测试,并且通过有限元仿真对发电机的振动特性进行进一步分析,通过ANSYS 软件对发电机进行模态分析,得到发电机定子的固有频率和振型。使用Workbench 软件进行响应分析,得到发电机定子的振幅响应曲线和响应频率,并将发电机定子的实测数据和模拟数据进行比较分析,为风力发电机振动的优化设计和有限元仿真提供了有效的依据。
1 发电机定子的现场测试
1.1 基本数据
该型风力发电机为直驱永磁式发电机,其额定转速为10.5 r/min,额定功率为3.2 MW,电机极对数为48 对。
1.2 现场测点布置
现场共布置两个测点,分别沿发电机定子的6 点钟方向和9 点钟方向,其测点布置如图1 所示。使用PCB 低频加速度振动传感器和EZ-TOMAS 旋转机械测试分析系统,将振动传感器紧贴在测点位置,通过信号采集装置即可得到该测点的时域信号,随后,对时域信号进行傅里叶变换,即可得到该测点的频谱图。分别对发电机定子在不同转速下的振动加速度进行了测试,采样频率为200 Hz。

图1 发电机定子测点布置Fig.1 Layout of measurement points for generator stator vibration test
1.3 振动测试结果
图2 为发电机定子不同方向振动加速度的通频值随转速变化的对比结果,可以看出,发电机定子加速度在叶轮转速为9.5 r/min 时达到峰值,同时,在不同转速下,定子6 点钟方向的加速度均高于9 点钟方向的加速度,在转速为9.5 r/min 时,定子6 点钟方向的加速度与9 点钟加速度的比值为6.44。在该转速下,发电机的基频为7.6 Hz。随后,对该转速下的频域信号进行了分析,结果如图3 所示,从图中可以看出,发电机定子的加速度振动信号来源主要为6 倍基频(45.6 Hz)和18 倍基频(136.8 Hz)。

图2 发电机定子不同方向振动加速度随转速的变化Fig.2 Vibration acceleration of generator stator in different directions varies with speed

图3 发电机定子不同方向振动加速度的通频分量对比Fig.3 Vibration acceleration in different directions of generator stator
2 发电机定子的有限元仿真
2.1 模态理论分析
结构的固有频率和振型可通过模态分析求得,模态是结构固有的振动特性,利用哈密顿原理、应力-应变关系及应力-位移关系,对于一个自由度为n的振动系统的微分方程可表示为[25]

发电机的模态分析属于无阻尼自由振动问题,即[R]=[0]和F(t)=[0],则式(1)为

当结构发生简谐振动时

由式(2)和式(3)可得

解特征值方程det(K-ω2M)=0 可得其固有频率,将每一个频率代入式(4),可得特征值矢量,进行归一化即可得到固有振型[26-27]。
2.2 模态仿真分析
由于振动测试以发电机的定子为主,因此,可以对发电机的模型进行简化,主要由定轴、定子机架和定子铁芯3 个部件组成,建立模型时,去除不影响计算结果的倒角、小的光孔和螺栓孔等。发电机定子模型如图4a 所示,采用自适应的网格剖分方式对模型进行网格剖分,其有限元网格模型如图4b所示,在保证网格精度的前提下,共有450 346 个节点、142 912 个单元。

图4 发电机定子的结构图Fig.4 Structure of generator stator
通过有限元软件计算分析,得到该机型发电机的各阶振型和固有频率,由于高阶模态对发电机振动特性影响较小,因此,只考虑若干低阶模态,表1为发电机定子的低阶固有频率。从表中可以看出,相邻两阶的固有频率值接近,这是由于模型的对称性导致式(4)出现了重根[28]。

表1 发电机定子的固有频率Tab.1 Natural frequency of generator stator
图5a 为发电机定子一阶振型x方向位移云图,其固有频率为22.489 Hz,振型为定子绕节径轴向振动;图5b为发电机定子二阶振型x方向位移云图,其固有频率为22.884 Hz,振型与一阶振型相似,只是节径位置发生了变化;图5c 为发电机定子三阶振型x方向位移云图,其固有频率为45.746 Hz,振型相对一、二阶振型发生了明显变化;图5d 为发电机定子四阶振型x方向位移云图,固有频率为46.073 Hz,振型图与三阶振型相似。

图5 发电机定子不同振型x 方向位移云图Fig.5 x direction displacement cloud image of generator stator with different modes
图6 为发电机定子在不同振型下沿圆周方向的x方向位移变化关系图,其中,横坐标为圆周角度,圆周方向以图5 中坐标轴-z方向为起始点;纵坐标为该角度下定子机架x方向的最大位移。从图6 可以观察到,发电机定子的位移沿圆周角度呈现明显的正弦波形,其中,一、二阶振型为一个周期的正弦图像,如图6a、图6b 所示;三、四阶振型为两个周期的正弦图像,如图6c、图6d 所示。

图6 发电机定子在不同模态振型下x 方向位移沿圆周方向变化关系Fig.6 The relationship diagram of the displacement of the generator stator in the x direction along the circumferential direction under different modal vibration shapes
2.3 响应分析
由于在实际运行过程中,发电机定子会受到转子施加的周期力矩的影响[29],因此,为了更加真实地模拟实测情况,需要对发电机定子进行响应分析。在发电机定子铁芯表面施加恒定的弯矩,测试的响应频率为0~50.0 Hz,中间间隔为0.5 Hz,最后测得x方向位移和频率之间的变化如图7 所示。从图中可以看出,较为明显的两个响应点分别为23.0 Hz 和43.5 Hz,与模态分析的求解结果接近。

图7 发电机定子x 方向位移与频率之间的响应分析图Fig.7 Response analysis between the displacement in the x direction and frequency of generator stator
图8 为发电机定子在频率为23.0 Hz 时的x方向位移云图,从图中可以明显观察到节径的存在,其位移云图与一、二阶模态振型相似。
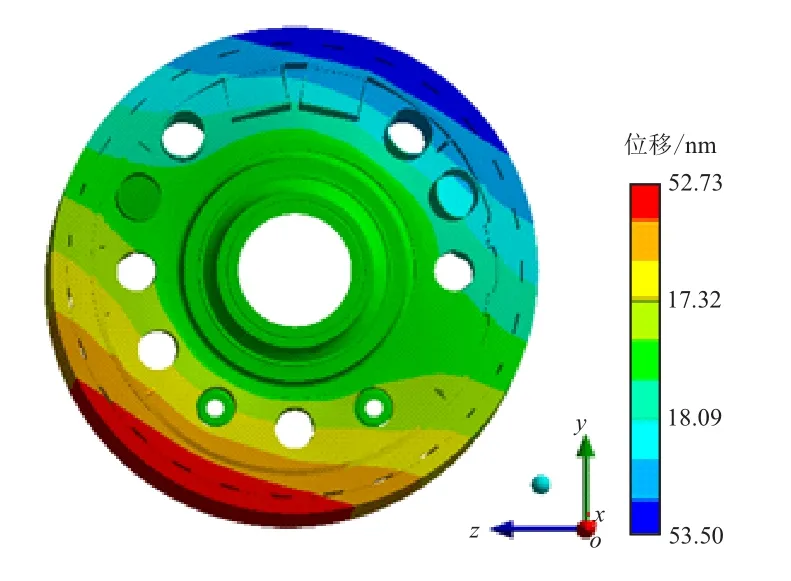
图8 发电机定子x 方向位移云图(23.0 Hz)Fig.8 Cloud diagram of generator stator displacement in x direction(23.0 Hz)
由实测数据可知,发电机定子在转速为9.5 r/min 时加速度最大,此时发电机的基频为7.6 Hz;由响应分析的仿真数据可知,发电机定子的响应频率分别为23.0 Hz 和43.5 Hz,其中,23.0 Hz与发电机的基频恰为3 倍的关系。并且振动加速度信号主要来源的6 倍基频和18 倍基频也与23.0 Hz有一定的倍数关系,可能是在该转速下,发电机的电磁激励频率接近23.0 Hz,导致发电机定子振动响应显著增大,同时激发了6 倍基频和18 倍基频的振动,应该在后续的运行过程中避开此响应点的出现。
与发电机定子的实测测点一致,分别在6 点钟方向和9 点钟方向选取一个测点,测点x方向位移随频率的变化如图9 所示。6 点钟方向测点的响应频率为23.0 Hz,位移为44.0 nm,在该频率下,9 点钟方向测点的位移为6.5 nm。两个测点的位移比值为6.70,实测两个测点的加速度比值为6.44,误差值仅为1%,确定了有限元仿真的合理性。在实测过程中选取的测点太少,不能完整反映发电机定子的振动状态,在后续测试中应该增加测点。
3 结论
(1)实测结果表明,发电机定子加速度在叶轮转速为9.5 r/min 时达到峰值,同时,在不同转速下发电机定子6 点钟方向的加速度均高于9 点钟方向的加速度,加速度振动信号来源主要为6 倍基频和18 倍基频。
(2)发电机定子响应分析结果表明,发电机在频率为23.0 Hz 和43.5 Hz 时振动较大,这与模态分析结果较为一致。在频率23.0 Hz 下6 点钟方向和9点钟方向的位移比值与实测加速度比值接近,确定了有限元仿真方法的正确性。同时,频率23.0 Hz与电机在转速为9.5 r/min 时的基频呈一定的倍数关系,关于更深的原理分析还有待于进一步机械与电磁联合动力研究。
(3)振动测试在测点较少的情况下不能完整反映发电机定子的振动情况,应该适当增加测点。
