永磁同步电机三电平模型预测转矩开关频率优化策略

於 锋，朱晨光，吴晓新

（南通大学 电气工程学院，江苏 南通 226019）

相较于传统的工业电机，永磁同步电机（permanent magnet synchronous motor，PMSM）具有低损耗、高效率、小体积等优势，在冶金、化工、石油、汽车等领域备受瞩目[1-4]。传统的PMSM 控制策略主要包括矢量控制（vector control，VC）和直接转矩控制（direct torque control，DTC）。VC 旨在将采集到的电机定子电流分解成相互独立的励磁分量和转矩分量以获得类似直流电机的动态特性，但控制过程不可避免地存在复杂的坐标变化与解耦的问题；DTC摒弃了传统VC 中的解耦控制及电流反馈环节，采取定子磁链定向控制方法，加快了响应速度，但是控制过程中计算量较大，也提高了对实时性的要求[5-6]。随着半导体器件制造工艺的提高与微处理器技术的发展，模型预测控制（model predictive control，MPC）逐渐受到国内外学者的广泛关注[7-9]。根据控制目标不同，用于电机驱动系统的MPC 主要集中于电流与转矩控制，即模型预测电流控制（model predictive current control，MPCC）与模型预测转矩控制（model predictive torque control，MPTC）[10-12]。其中，MPTC 利用价值函数直接对转矩进行约束，计算并比较不同开关状态对应的价值函数大小，将最优开关状态作用于逆变器，实现转矩优化跟踪。

二极管中点钳位式（neutral-point-clamped，NPC）三电平逆变器凭借其应用场合功率高、电流谐波含量低等优点在变频调速系统中得到广泛应用[13-15]。然而，NPC 三电平逆变器的应用存在影响系统控制性能的中点电位波动的问题。基于此，文献[16]分析了冗余小矢量对中点电位作用效果，提出一种利用正负小矢量之间合理替代的方法进行中点电位平衡控制。值得注意的是，NPC 三电平逆变器存在27 个空间电压矢量，需要进行27 次重复计算，才能在滚动优化之后筛选出最优电压矢量，这一过程极大增加了系统的运算负担。文献[17-18]通过构建磁链和转矩的偏差，利用不同电压矢量对磁链偏差产生的不同影响，筛选出对抑制磁链偏差有利的电压矢量参与滚动优化，从而将备选矢量减少至14个；但文献[17-18]均未对逆变器的开关频率作出约束，较高开关频率会导致开关器件的损耗加剧、发热严重，甚至还会影响开关器件的使用寿命。针对上述问题，本文提出一种PMSM 三电平MPTC 开关频率优化策略。首先，通过构建限制开关状态切换的矢量筛选策略和包含开关频率约束项的MPTC 价值函数，在减小系统计算负担的基础上有效降低系统的开关频率；其次，利用正负小矢量的反向特性进行合理替换来实现中点电位平衡控制；最后，通过仿真和实验的验证，表明该控制策略的有效性。

1 数学模型

本文研究对象为内嵌式PMSM，建立dq坐标下的电机数学模型。得到的定子电压方程为

式中：u、i、ψ 分别表示定子电压、定子电流、定子磁链；下标d和q标识dq坐标系下的分量；R为定子电阻；ωe为电角速度。

磁链方程为

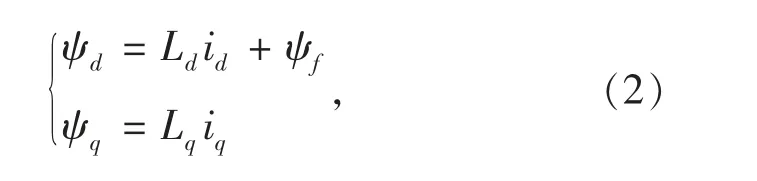
其中：L表示定子电感；ψf为永磁体磁链。

结合式（1）和（2）得到定子电压方程为

电磁转矩方程为

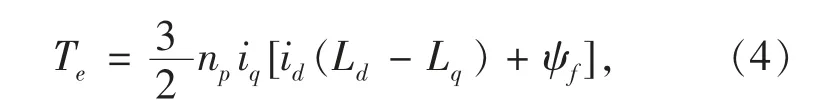
其中：Te为电磁转矩；np为极对数。

2 模型预测转矩控制

2.1 模型预测转矩控制框图

图1 NPC 三电平PMSM MPTC 系统框图Fig.1 MPTC block diagram of PMSM supplied by three-level NPC inverter

2.2 转矩预测模型

改写式（3），可得

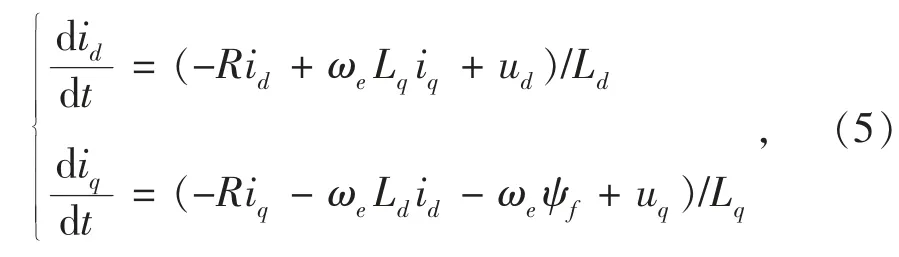
利用欧拉方程

对式（5）进行离散化处理，得到电流预测方程为

其中：x（k+1）为k+1 时刻的预测状态；x（k）为当前时刻状态；上标k+1 与k分别标识k+1 时刻的预测值与k时刻测量值；Ts为采样时间。

将式（7）代入式（2）得到k+1 时刻dq轴磁链预测值分别为

通过三角函数变化得到k+1 时刻合成磁链的预测值为

将式（7）代入电磁转矩方程（4）中，得到k+1 时刻转矩的预测值为

结合式（9）和（10）构建MPTC 价值函数，得到

其中λ1为磁链项权重系数，一般以额定转矩与额定磁链的比值为初值，通过仿真与实验进行调节得到最优权重。

2.3 计及开关频率优化的控制策略

NPC 三电平逆变器在空间上存在27 个基本电压矢量，如图2 所示。需要经过27 次价值函数的滚动优化来确定满足最小化价值函数输出的电压矢量，在多步预测和多矢量控制中，价值函数的滚动优化次数更是呈指数形式递增。此外，由于缺乏对开关状态切换的约束条件，在一个采样周期中可能存在多个开关状态同时切换，导致逆变器产生较高的开关频率，加剧了开关器件的损耗和发热现象，降低了其使用寿命。因此，本文设计了限制开关状态切换的矢量筛选策略和包含开关频率约束项的价值函数，在减少备选矢量的同时有效降低系统的开关频率。

图2 NPC 三电平逆变器的空间矢量分布Fig.2 Spatial vector distribution of three-level NPC inverter

为减少备选矢量的数量并限制开关状态的切换，构建了如表1 所示的限制开关状态切换的矢量筛选表。首先，以k-1 时刻作用矢量为中心，设定前后30°范围内的电压矢量为备选矢量，数量为8～10 个。其次，为降低开关频率，在相邻采样周期内最多允许两相开关状态发生变化，且遵循仅切换一个开关管的原则，即满足2∶1∶0。经过上述步骤备选矢量的数量降低至4～7 个。

表1 限制开关状态切换的矢量筛选表Tab.1 Vector screening table considering switch state switching restriction

经过表1 的矢量筛选表，能够在一定程度上限制开关的跳变。为进一步降低开关频率，在价值函数中加入对开关频率的约束条件。定义k-1 时刻开关状态为S（k-1）=[Sa（k-1），Sb（k-1），Sc（k-1）]，其中Sx（k-1）∈{0，1，2}，x∈{a，b，c}；定义k时刻的开关状态为S（k）=[Sa（k），Sb（k），Sc（k）]，其中Sx（k）∈{0，1，2}。可以构建开关状态偏差方程为

将式（12）并入MPTC 的价值函数（11）中能够得到包含开关频率约束项的MPTC 价值函数

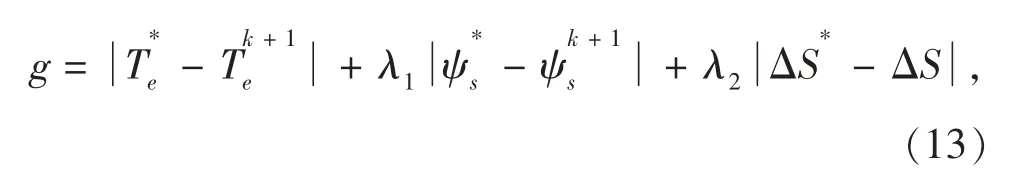
其中：λ2为开关频率约束项的权重系数；ΔS*=0 表示理想的开关状态偏差。

2.4 中点电位平衡控制

NPC 三电平PMSM 等效模型如图3 所示。相较于传统两电平逆变器，NPC 三电平逆变器电压应力更低，控制性能更好，但是也存在中点电位不平衡的缺陷，若不加以控制，将会影响整个系统的控制性能，严重时会导致系统失控甚至损毁开关器件。实际上，中点电位波动的根本原因在于直流侧分压电容充放电不平衡，表现为电容中性点电流不为0。NPC 三电平逆变器中点电流inp可表示为

图3 NPC 三电平PMSM 等效模型Fig.3 Equivalent model of PMSM supplied by three-level NPC inverter

通过对如图3 所示的NPC 三电平PMSM 等效模型分析可知，在零矢量作用下，电机和直流电源之间不构成闭合回路；而在大矢量作用下，电路的导通路径不经过中性点，因此零矢量和大矢量的应用不影响中点电位的波动。进一步地，分析小矢量和中矢量对中点电位的影响如表2 所示，可以看出，中矢量的应用导致中点电位减小，而具有相等幅值、相同方向的正负小矢量对于中点电位的影响效果相反。例如矢量100 与211 同为小矢量，幅值相等，方向一致，但100 降低中点电位，而211 增大中点电位。基于这一特性，利用正负小矢量之间合理替代的方法进行中点电位平衡控制。

表2 中矢量与小矢量对中点电位U0 的影响Tab.2 Effect of medium vector and small vector on the neutral potential U0

3 仿真验证

为验证本文所提出的基于开关频率优化的三电平MPTC 算法的可行性，利用MATLAB/Simulink对所提控制算法进行了仿真验证。仿真中PMSM 参数设置如表3 所示。此外，直流母线电压设置为300 V，逆变器直流侧分压电容选用470 μF，系统采样频率为20 kHz，权重系数λ1设置为30，λ2设置为0.2。

表3 PMSM 主要参数Tab.3 Main parameters of PMSM

3.1 NPC 三电平逆变器线电压与中点电位仿真

图4 为两电平逆变器与三电平逆变器线电压仿真波形。通过对比发现，相较于传统两电平逆变器，三电平逆变器线电压具有5 个电压梯度，输出波形更接近正弦波。可见三电平逆变器对于提高波形质量具有明显优势。

图4 两电平逆变器与三电平逆变器线电压仿真波形Fig.4 Simulation results of line-voltage with two-level inverter and three-level inverter

图5 为NPC 三电平逆变器中点电位仿真波形。在t=1.0 s 前不进行中点电位平衡控制，此时，中点电位迅速上升，且电流波形的正弦度变差。在t=1.0 s 时应用中点电位平衡控制策略，中点电位能迅速由150 V 的偏移量回到0 V，且能保持恒定，同时A 相电流波形有较好的正弦度。

图5 NPC 三电平逆变器中点电位仿真波形Fig.5 Simulation results of neutral potential with three-level NPC inverter

3.2 NPC 三电平逆变器MPTC 开关频率仿真

为验证本文所提出的开关频率优化控制策略的可行性，将本文提出的计及开关频率优化的NPC三电平MPTC 与传统的三电平MPTC 进行比较。图6 为开关频率仿真波形，运行工况设置为给定转速300 r/min，给定负载4 N·m。其中，图6（a）为传统NPC 三电平MPTC 算法，不考虑对开关频率的约束；图6（b）为本文所提出的计及开关频率优化的NPC 三电平MPTC 算法。通过对图6 进行分析可知，传统的NPC 三电平MPTC 策略的开关频率较高，在20 kHz 的采样频率下，开关频率达到22.5 kHz；而本文所提出的低开关频率的NPC 三电平MPTC 策略在同样20 kHz 的采样频率下，开关频率仅为13 kHz。

图6 NPC 三电平MPTC 开关频率仿真波形Fig.6 Simulation results of switching frequency associated with MPTC in three-level NPC inverter

4 实验验证

为验证理论分析的正确性，搭建了一台2.2 kW三电平供电式PMSM 实验平台，如图7 所示。其中直流母线电压、三相电流分别采用LV25-P 电压传感器与HAS50-S 电流传感器进行测量。同时，OMRON编码器用于获取转子位置信号。具体电机参数如表3 所示，实验直流母线电压设置为300 V，采样频率为5 kHz，权重系数λ1设置为30，λ2设置为0.2。

图7 实验平台Fig.7 Experimental platform

4.1 NPC 三电平逆变器线电压与中点电位平衡

图8 为NPC 三电平逆变器线电压实验波形，可见NPC 三电平逆变器线电压实验波形中有5 个电压梯度，能保证良好的正弦电压输出。图9 为中点电位平衡实验波形，可以看出，若不进行中点电位平衡控制，直流侧分压电容电压偏差较大，中点电位达到120 V，且A 相电流严重畸变，而在加入中点电位控制策略后，直流侧分压电容电压快速平衡，中点电位下降至0 V，同时，A 相电流波形畸变减小。

图8 NPC 三电平逆变器线电压实验波形Fig.8 Experimental results of line-voltage with three-level NPC inverter

图9 中点电位平衡实验波形Fig.9 Experimental results of neutral potential balance

4.2 NPC 三电平逆变器MPTC 开关频率优化

在给定转速300 r/min、给定负载4 N·m 的条件下进行开关频率优化，结果如图10 所示。图10（a）为传统MPTC 策略，开关频率为4 kHz；图10（b）为低开关频率的MPTC 策略，开关频率为2.6 kHz。可以观察到图10（a）和图10（b）均能够获得较好的稳态性能，但图10（b）所示的低开关频率MPTC 策略能够有效降低开关频率。

图10 开关频率实验波形Fig.10 Experimental results of switching frequency optimization with MPTC in three-level NPC inverter

5 结论

为降低系统的开关频率，本文提出一种PMSM三电平MPTC 开关频率优化策略。首先，通过限制一个采样周期内开关状态的变化方式并构建包含开关频率约束条件的MPTC 价值函数，将备选矢量筛选至4～7 个的同时有效降低系统的开关频率；然后，利用正负冗余小矢量对中点电位作用效果相反的特性实现中点电位的平衡；最后通过仿真和实验验证了该控制策略的有效性。