机器人视觉中目标物的位姿估计改进

张 磊，张天益，姚兴田，吕栋阳

（1.南通大学 机械工程学院，江苏 南通 226019；2.约克大学 拉松德工学院，加拿大 多伦多，M3J 1P3）

目标物的位姿估计问题是指通过数学建模等方式解出摄像机与目标物之间的相对位置关系，在摄影测量、交通视觉导航及视觉机器人作业等领域具有重要的应用价值。知名的波士顿动力机器人Atlas 实现目标物抓起动作即先对目标纸箱进行位姿估计[1]。位姿估计旨在获得目标物在摄像机坐标系中的位置与姿态，为基于图像对目标物进行下一步操作做准备。

常见的位姿估计方法是由摄像机标定获得内参数，然后由n 个3D-2D 点对点的对应关系恢复物体位姿，被称作PNP（perspective n point）问题，由Fischler 等[2]首先提出。关于P3P、P4P、P5P 等解的存在性、唯一性、多解性、最优解等问题已得到充分研究。近年来有不少基于PNP 解法进行优化或应用的报道[3-7]。Xu[3]提出了一种基于线对应的位姿估计方法，与PNP 的点对应经典方法对比，在精确性与鲁棒性方面都有所提升；Lepetit 等[8]提出了基于封闭解的EPNP（efficient perspective-n-point）方法，在精度上相对于经典PNP 方法有了较大提升，但该方法过程比较复杂，他人难以在其基础上进行改进。第二类是借助摄像机标定的方法获得目标物的位姿，典型的有直接线性变换（direct linear transformation，DLT）方法[9]与张正友方法[10]。这些方法需要很多的特征点，对于一般的目标物，大量特征点的对应是个较难的问题；而特征点少，此类方法的精度又会明显下降。针对这些问题，文献[11]对DLT 方法作了一定改进。第三类是基于目标物CAD 模型的方法，以Bhanu[12]的研究和Harris[13]的RAPiD 方法最为经典。近期有Tsai 等[14]的研究，较为详细的介绍可参见Lepetit 等[15]的综述。但这类方法需要将CAD模型与图像同时在一个图像场景中匹配，技术上的实现难度增大，且边缘点难对应的问题会影响其成功率。

为了提高上述方法的精度，常采用非线性优化，其中较为常用的是最速下降法、高斯牛顿法和列文伯格-马夸尔特（Levenberg-Marquardt，LM）算法[16]。LM 算法[17-18]吸收了高斯牛顿法可避开求解Hessan二阶导数矩阵的优点，避免了高斯牛顿法因雅可比矩阵不满秩而造成的麻烦；其设计了一种信赖域策略，使得迭代的步长是动态的，进一步提高了非线性优化的效率。Yan 等[19]提出基于三次多项式的代价函数，基于此设计了相关的非线性迭代算法，获得精确的位姿估计。

本文针对经典DLT、EPNP 等解析法存在位姿估计精度不高的问题，利用相对简单的DLT 方法获得估计初始值；根据LM 优化算法的特点，提出了方便求解雅可比矩阵的代价函数，并引入李群李代数表达位姿微调矩阵，进一步简化了雅可比矩阵的求解和位姿参数值的迭代估计。

1 经典的DLT 方法及其计算

DLT 线性模型根据摄像机小孔成像原理，不考虑镜头畸变等非线性因素，直接以线性变换的形式建立靶标特征点的世界坐标（X，Y，Z，1）T与相应图像坐标（u1，v11）T的关系

将s消去得

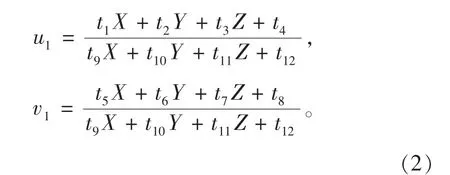
传统解法[16]一般将式（2）分别变形为

其中：t1=（t1，t2，t3，t4）T，t2=（t5，t6，t7，t8）T，t3=（t9，t10，t11，t12）T；P=（X，Y，Z，1）T。

对于N 个特征点，可列出方程组

但该方程无法使用直接的线性方程组解法，因为右边全是0 元素。常见的解法是采用奇异值分解法（single value decomposition，SVD）[16]。然而SVD 方法需要求解系数矩阵的奇异值及奇异向量，求解过程繁琐。当矩阵维数较大时，需使用数值或迭代解法，求解的过程已失去封闭解法的简便性。

文献[20]中将式（2）上下同除以t12变换为

本文利用该形式，结合文献[21]的思想，得到

其中：（ui，vi）T是第i个特征点的图像坐标；=（Xi，Yi，Zi）T是第i个特征点的世界坐标。该方程记为

此方程可利用广义逆直接求出封闭解

由于t′中的元素与tm（m=1，2，3）中的元素满足

所以需先解出t12，才可解出t1，t2，…，t11。

根据摄像机投影中的内外参数关系，式（1）可表达为

其中：fx，fy，cx，cy为摄像机内参数；为外参数旋转矩阵的各行向量；px，py，pz为外参数平移向量的各元素，外参数即待求解的位姿参数，因此

按照向量叉乘、点乘性质，先可解得内参数，然后可得各外参数

研究发现，当目标物特征点不多时，该方法精度偏低，因此本文通过非线性优化方法进行了改进。

2 基于LM 算法的简化优化方法

LM 算法虽然是经典通用方法，但是其本身并没有提供具体的设计函数、参数配置等。实际应用时，需根据实际问题设计恰当的代价函数，方便求解雅可比矩阵J，找到合适的迭代过程。

2.1 代价函数的设计

摄像机标定和图像位姿估计常用平均反投影误差衡量参数估计的偏差，即

其中：（ui，vi）为由估计的参数根据式（11）结合镜头畸变参数进行反投影计算得到的第i个特征点的图像坐标；为直接检测到的相应控制点图像坐标，单位为像素。Err值越小代表估计参数越精确，一般基于此设计代价函数进行非线性迭代优化。式（15）含有根号和求平均值项，对非线性优化来说不是必须的，会增加雅可比矩阵计算的复杂性，本文基于式（15）提出的代价函数为

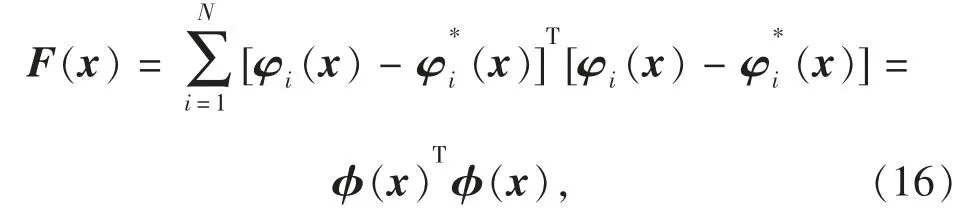
其中：

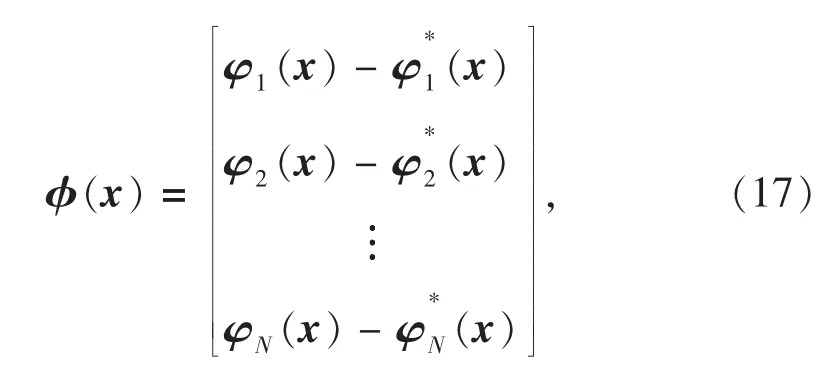
φ（x）为反投影误差向量，x为待求解或待优化的未知量构成的向量；，i 为图像特征点（控制点）编号，共N 个。根据非线性优化的要求[22]，可仅对φ（x）求解雅可比矩阵，且各为常值，大大简化了雅可比矩阵的求解。

2.2 位姿估计的参数化表达

φi（x）不仅与式（11）中的诸多内外参数有关，还与摄像机畸变系数有关，若对所有参数进行迭代优化，计算过程繁琐。为避免复杂的求解过程，先通过张正友标定方法确定摄像机内参及畸变系数，使φi（x）仅是旋转矩阵和平移向量的函数，记为

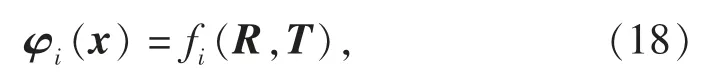
其中旋转矩阵R的各行向量或列向量两两正交，它们虽然有9 个元素，但独立元素仅3 个，因此不宜直接对式（18）求雅可比矩阵。

将旋转矩阵R表达为3 个独立变量的经典欧拉角

其中α，β，γ 分别代表绕z 轴的翻滚、绕y 轴的俯仰、绕x 轴的偏转。但该形式仍然不利于求解雅可比矩阵，且存在万向节死锁的可能而引入病态解[15-16]。本文引用近年来流行的李群李代数法[16，23]来表达相关旋转矩阵。

根据摄像机小孔投影模型，投影矩阵由内外参数矩阵构成，记为MP=KE，其中K为内参数矩阵，E为外参数矩阵。内参数矩阵K由张正友方法标定获得。E的初始值由DLT 解法获得，之后每迭代一次对E微调获得更高精度的估计，得

其中：k 表示第k 次估计；Mk+1有与外参数矩阵类似的表达形式，定义为外参数微调矩阵。

引入李群李代数表达形式，将Mk+1基于群SE（3）的4 阶方阵形式，以6 维的李群来表达。SE（3）可表达输出的姿态空间，其指数映射可在微小变化时表达为线性映射的形式。构建代表x，y，z 轴移动与旋转的一组基为

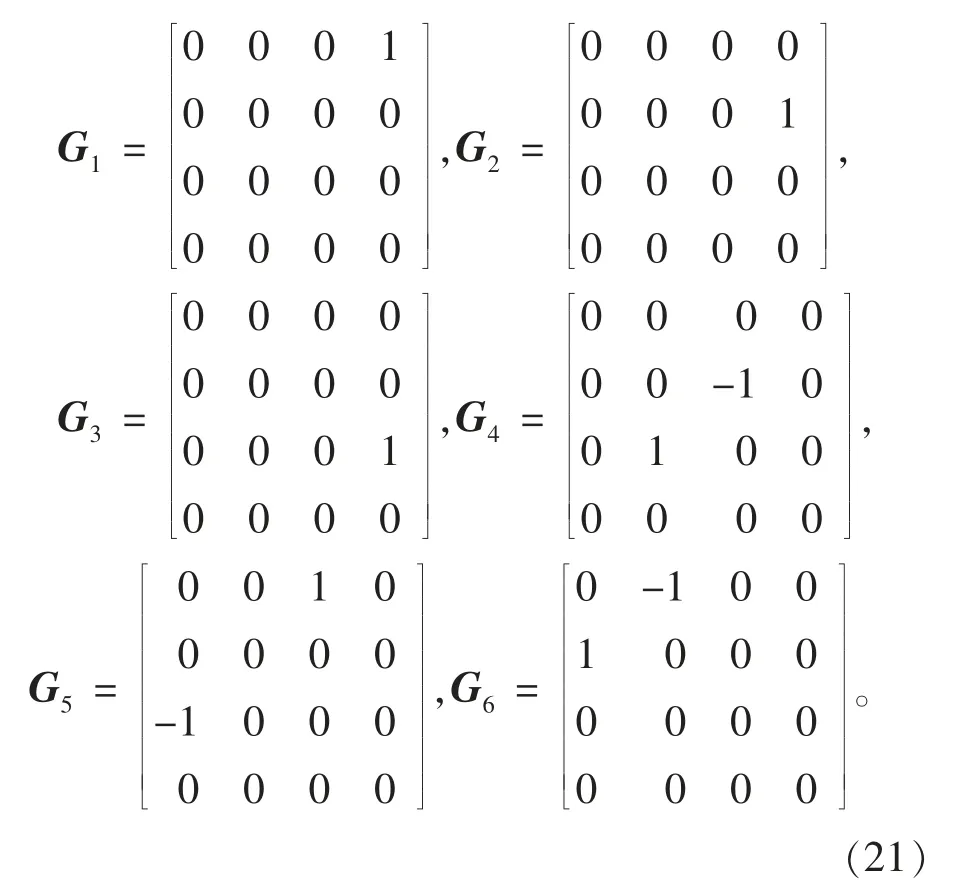
将Mk+1视为群中的元素，可由这些基通过指数映射获得，即

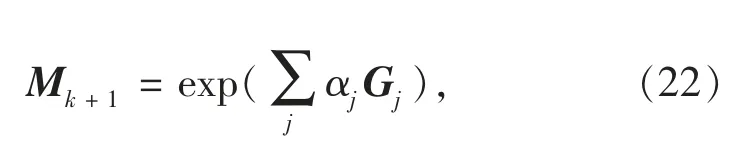
其中j 表示每个基及其因子的编号。因为Mk+1表达了一种微小的变化，根据指数映射泰勒展开，可用一阶线性近似地表达

通过这种表达，问题转化为求解各个αj。根据式（11）、（23）有

其中s为比例因子，即便有微小偏差，也可由ui，vi的相应变化而弥补，同时考虑到的变化量很小，将其略去，s可简化为一常数

2.3 雅可比矩阵求解及迭代优化

J 中的每个元素（第i行第j列）根据式（26），得

由式（28）可知，对于不同的控制点，其雅可比偏导只有世界坐标Pi不同，其余参数相同，有利于提高每次迭代的雅可比矩阵计算速度，简化了编程。

依据LM 算法的基本思路，第k+1 次的结果可由第k次按此迭代得到

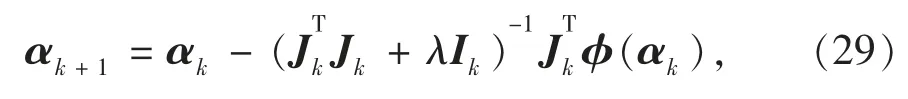
其中φ（αk）代表了第k次的反投影误差向量。文献[16，22]介绍了LM 算法的步长λ 计算方法，本文不再展开。每得到一个新的αk +1，根据式（20），（23）及时更新Ek+1=EkMk+1。迭代过程在‖αk+1-αk‖≤ε 时终止，ε 可由经验确定。

得到α 终值后，可由式（19）、（20）、（23）得到最终表达目标物姿态的3 个欧拉角。

3 实验与结果

本文的应用背景是机器人面临抓取等任务，需依靠机器人视觉先获得目标物位姿。为便于角点提取及确定姿态方位，设计了如图1 所示的两种木块及其背景。木块的顶点为指定控制点，在图像中特征为角点，图中坐标系为目标物的世界坐标系，所求的位姿即该坐标系相对摄像机的位置与姿态。

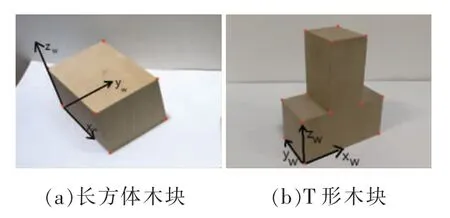
图1 位姿估计的两种目标物Fig.1 Two objects for pose estimation

3.1 位姿估计精度实验

为验证本文方法的精度，选择了经典的DLT 方法、EPNP 方法、DLT+数值LM 方法（即将DLT 方法与通用数值解法的LM 方法相结合）与本文方法进行对比。其中DLT 方法是线性解法；EPNP 方法虽不是典型线性解法，但仍然是一种封闭解；DLT+数值LM 方法是将DLT 方法作为数值LM 法的初始迭代值进行的一种非线性优化；本文方法将DLT 方法的初始值作为改进LM 算法的初始值。图2 为在摄像机1 倍焦距下的10 种姿态，表1 为长方体目标物在10 种位姿下经典的DLT 方法、EPNP 方法、DLT+数值LM 法与本文方法的位姿估计平均反投影误差对比情况。平均反投影误差按式（15）计算。可见DLT 方法反投影误差很大，EPNP 方法误差较小，本文方法的反投影误差比同样是非线性优化的DLT+数值LM方法明显更小。为了验证本文方法在更多统计情况下的效果，下面给出2 倍、3 倍焦距下该长方体在20种位姿下的位姿估计反投影误差平均值，见表2。由表2 的结果可知本文方法明显优于其他3 种方法。

表1 1 倍焦距下长方体木块位姿估计的平均反投影误差比较Tab.1 Error comparison of the pose estimation of the cuboid object for 1X focal length of the camera 像素

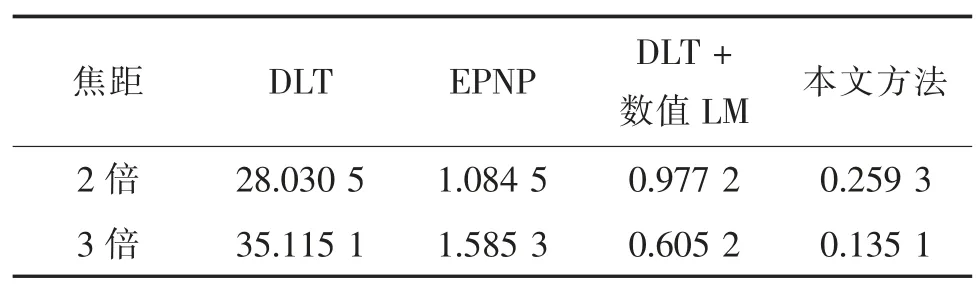
表2 不同焦距下长方体木块20 种位姿估计的平均反投影误差平均值Tab.2 Mean error comparison of 20 pose estimations of the cuboid object for different focal length of the camera 像素

图2 长方体目标物10 种位姿Fig.2 Ten poses of the cuboid object

接下来，对更为复杂的T 形木块在不同焦距各种姿态下的位姿估计进行实验，图3 为10 种典型T形木块的位姿。表3 为T 形木块在10 种位姿下DLT方法、EPNP 方法、DLT+数值LM 与本文方法的位姿估计平均反投影误差对比情况。为了获得大量的统计结果，表4 给出2 倍、3 倍焦距下T 形体在20 种位姿下的位姿估计平均反投影误差的平均值。从表3～4 结果可知，DLT 方法的平均反投影误差依然很大，EPNP 方法误差较小，本文方法的平均反投影误差比同样是非线性估计的DLT+数值LM 方法仍然更小。

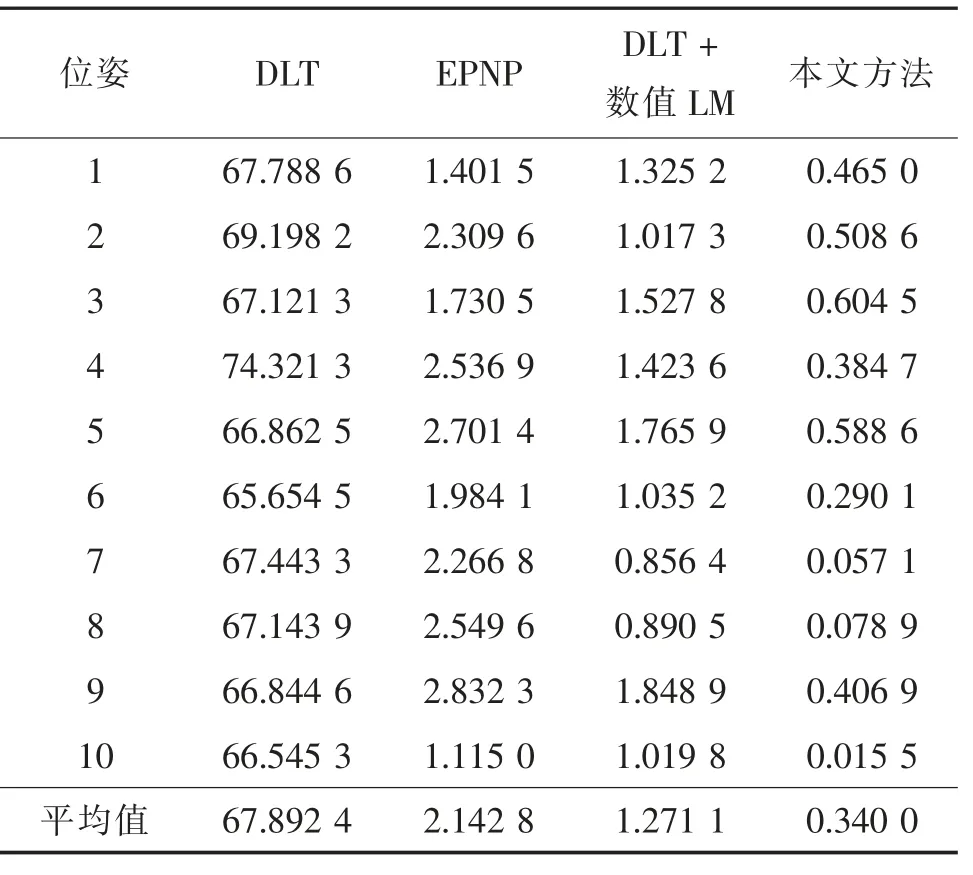
表3 1 倍焦距下T 形木块位姿估计的平均反投影误差比较Tab.3 Error comparison of the pose estimation of the T-shaped object for 1X focal length of the camera 像素

表4 不同焦距下T 形木块20 种位姿估计的平均反投影误差平均值Tab.4 Mean error comparison of 20 pose estimations of the T-shaped object for different focal length of the camera 像素

图3 T 形目标物10 种位姿Fig.3 Ten poses of the T-shaped object

表5 列出了6 组实验的最终总平均反投影误差平均值。结果表明提出的改进方法比经典的几种方法在估计精度方面均有较大提升。

表5 不同方法位姿估计的总平均反投影误差平均值比较Tab.5 Total mean error comparison of the pose estimation for different methods 像素

3.2 本文方法合理性验证

本文设计了将长方体木块与标定板相帖合的方式，将两者的世界坐标系完全重叠定义，如图4所示。将本文方法得到的位姿值与张正友标定法得到的外参数比较以确认本文方法的合理性。表6 列出了如图4 所示的目标物位姿具体值和张正友外参标定值。通过对比可知，两者数值十分接近，其他结果也是类似的，不一一列出。这说明了本文方法得出的结果是合理有效的。

图4 目标物与标定板帖合的布局Fig.4 Alignment configuration of the object and the calibration board

表6 本文方法与张正友方法的比较Tab.6 Comparison of the proposed method and Zhang′s method

3.3 耗时对比实验

相比于经典的DLT 与EPNP 解析法，非线性优化是一个迭代过程，而且其中夹杂着雅可比矩阵计算、广义逆矩阵计算等耗时环节，所以正常情况下非线性优化耗时将会明显多于封闭解析法，因此只对两种非线性优化进行了耗时测试。本实验所运行的计算机是普通的个人笔记本电脑，CPU 为第9 代英特尔i7-9750H，主频2.6 GHz。

图5 显示了长方体木块在1 倍焦距下的10 种位姿估计的两种方法耗时情况。表7 列出了6 组实验的总体平均耗时。结果显示本文改进方法与DLT+数值LM 方法相比，耗时更少，表明本文改进方法计算过程更简便、迭代更少。本文方法的总体平均耗时均少于90 ms，最终平均耗时为67.48 ms，本文方法能满足图像处理领域软实时的要求（允许每帧100 ms 左右处理时间）。

图5 1 倍焦距下长方体木块位姿估计耗时Fig.5 Time consuming of the pose estimation of the cuboid object for 1X focal length of the camera

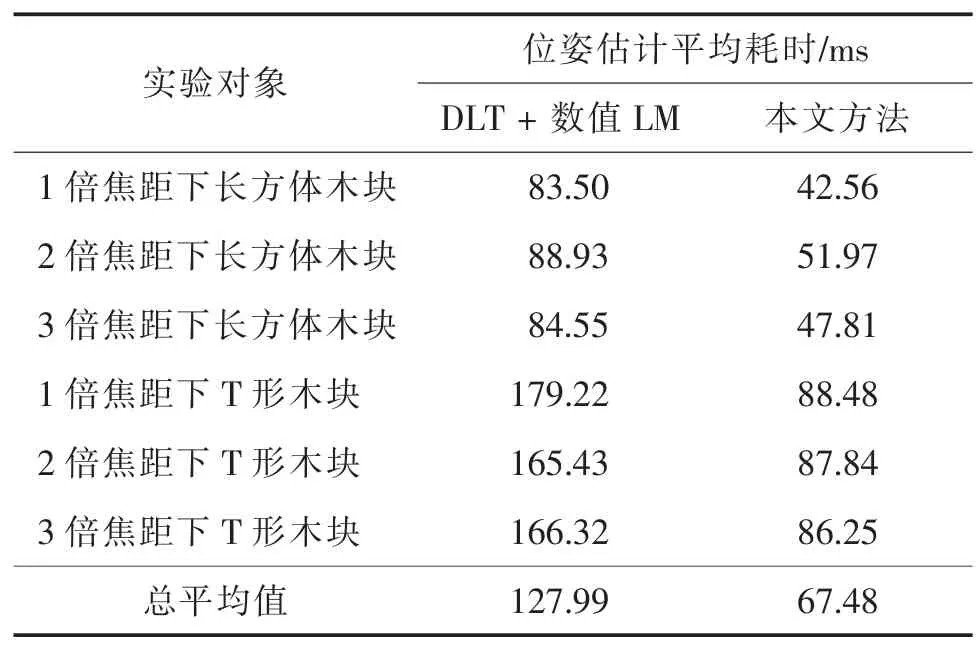
表7 不同方法位姿估计的平均耗时比较Tab.7 Average time consuming of the pose estimation for different methods

4 结论

本文研究了精度更高、求解相对简单的目标物三维位姿改进方法。实验结果表明，本文提出的改进方法比经典DLT 方法、EPNP 方法在精度上有明显提高，也比同样是非线性优化的DLT+数值LM 算法精度有所提高。该方法由于简化了雅可比矩阵计算，实现更为容易，非线性优化总体耗时也比DLT +数值LM 方法更少。因此，本文研究的位姿估计改进方法可为机器人视觉提供更准确而及时的信息，满足机器人操作目标的实时性要求，具有良好的实际应用价值。