空间相关多点地震位移输入峰值控制对结构非线性响应的影响
2022-01-12陈科旭俞瑞芳孙平宽
陈科旭,俞瑞芳,孙平宽
(1.中国地震局地球物理研究所,北京100081;2.中国公路工程咨询集团有限公司,北京100089)
引言
合理的地震动输入是结构进行抗震分析的前提条件[1]。地震动受传播路径、距离及场地条件等因素的影响,在时间和空间上都具有复杂的变化,对于平面尺寸较小的建筑物,地震动在空间不同观测点的差异变化影响通常可以忽略不计,在进行结构抗震分析时,各个支撑点处可以采用同样的地震动输入;但是对于大尺度空间结构,如长大桥梁、隧道、渡槽,以及管线、输电塔等生命线工程,地震动的空间变化将对其产生重要影响[2],因此大尺度空间结构采用多点地震动输入更加符合实际的输入模式[3-4]。结构抗震设计理论从一致地震动输入发展到多点地震动输入是一个巨大的飞跃。已有研究表明,与多点激励下的结构响应相比,一致激励往往明显高估或低估结构的某些响应[5-8],这些研究结果的差异除了和结构特性相关外,很大程度上在于对地震动输入的空间变化或非平稳特性描述不同[8]。基于工程实践的需要,能够表征地震动空间变化的相干函数模型及空间相关多点地震动拟合方法得到了很大的发展[9-13]。目前用于工程实践的相关多点地震动合成方法都是基于Hao等提出的三角级数法进行的[14],该方法假定地震动是一个平稳的随机过程,用相干函数来描述地震动的空间变化。由于相干函数是基于平稳随机过程假定给出的,其无法描述每个测点地震动强度和频率随时间的变化,因此工程中常采用具有统计参数的强度包线函数来反映地震动强度的非平稳特性。对频率的非平稳特性,可采用分段合成再叠加的方法,或通过地震加速度相位差谱分布来近似描述[15],或直接采用时-频包线函数来近似模拟地震动频率非平稳特性[16]。
目前,在通用有限元分析软件中,对大跨结构采用多点输入模式进行地震响应分析时,一般采用位移输入法和加速度输入法,其中位移输入法是直接在结构各基底输入地震位移时程,加速度输入法则是通过特殊的建模方式使结构基底的输入等效为各点的加速度时程[17],其实质是在上部结构上施加等效的地震荷载。现有的空间相关多点地震动拟合方法中,一般都是以加速度反应谱和加速度峰值为控制目标拟合得到结构不同支撑点的加速度时程,此时相应于不同支撑点处位移时程的峰值则是不同的;再者,由于地震动拟合中初始加速度时程采用随机相位,即使控制加速度时程的峰值相同,其相应的位移时程的峰值也有较大的离散性[18]。由于在场址地震动参数的估计中,目前的研究成果很难得到可应用于工程实践的位移峰值的估计方法[19],因此采用加速度峰值作为拟合目标进行地震动模拟是工程实践中必然的选择。此时,面临的问题是采用位移输入法进行结构非线性响应分析时,是否要控制位移时程的峰值?如何控制位移峰值?不同的控制条件会对结构响应产生怎样的影响?为了回答这些问题,本文首先基于不同的研究目标设计了地震动输入方案,模拟得到了能够表征地震动强度或频率特性的空间相关多点地震动,并且控制不同支撑点有相同的加速度峰值或位移峰值;然后采用多点地震动加速度/位移输入,对三跨连续梁桥进行了非线性时程响应分析,讨论不同的地震动输入特性和方案对结构响应的影响。本文的分析结果可为空间相关多点地震动人工拟合中关键控制参数的设置、地震动输入方案的选择提供理论依据。
1 大跨结构在多点地震加速度/位移输入下响应的计算方法
大跨空间结构在进行地震响应分析时,如果假定结构为集中质量体系,在结构基底各支撑点处施加不同的地震动输入,采用体系外的固定坐标系,用总位移表示各节点的运动,则结构的动力方程可以写为[20]
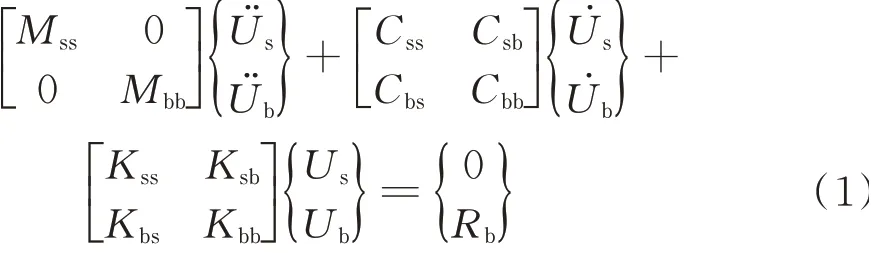
式中M,C,K为质量、阻尼和刚度矩阵,下标ss,bb,sb分别表示上部结构、支撑点和二者耦合项;分别表示上部结构的加速度、速度和位移响应分别表示下部支撑点处的地震加速度、速度和位移时程,一般为已知量;Rb为下部支撑节点上的反力。
展开式(1)中的第一行可得
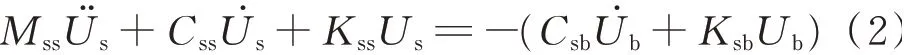
可以看出,如果已知地震位移激励Ub及相应的速度U̇b项,则求解方程(2)可得到上部结构的绝对位移响应Us。方程(2)是目前通用结构有限元分析软件中位移输入法(DM)[21]的基本方程,计算时首先释放支承处加载方向自由度,然后直接输入地震位移时程。相较于理论上的相对位移法,直接位移输入法在计算时不需预先提取质量、刚度、阻尼矩阵,这将大大简化前处理流程。
如果展开式(1)的第二行,则可得到
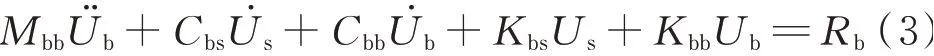
式中下部支撑节点上的反力Rb可以表示为

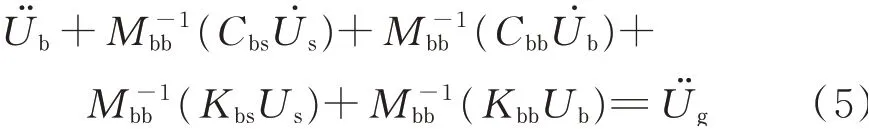
然而,基于方程(5)的LMM法计算得到的一般是结构响应的近似值,和位移输入法得到的精确值相比,LMM法计算得到的结构响应的某些量会产生较大的误差。如图1所示为一个三跨桥梁的桥墩扭矩和滑动支座位移,采用LMM法计算,其结构产生的最大误差达到了66.08%。现分析该误差产生的原因,若计算中结构阻尼假定是Rayleigh阻尼,即
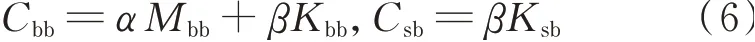
代入方程(5)可得

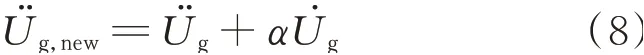
将式(6)和(8)代入式(5)中,则可以得到地震加速度Üg和支座处的实际响应加速度Üb之间更加精确的近似,文献[23]讨论了这种修正方法,并将这种修正了拟输入加速度的方法称为修正后大质量法(MLMM)。为了说明修正后大质量法的计算效果,将上述的3跨桥梁按照MLMM法计算得到的结果与位移输入法的计算结果进行了对比,结果如图1所示。可以看出,同样的输出量,采用MLMM法的误差大约为1%-2%。因此,在本文的研究中,将采用MLMM法和DM法进行多点加速度/位移输入下大跨结构的非线性响应分析。
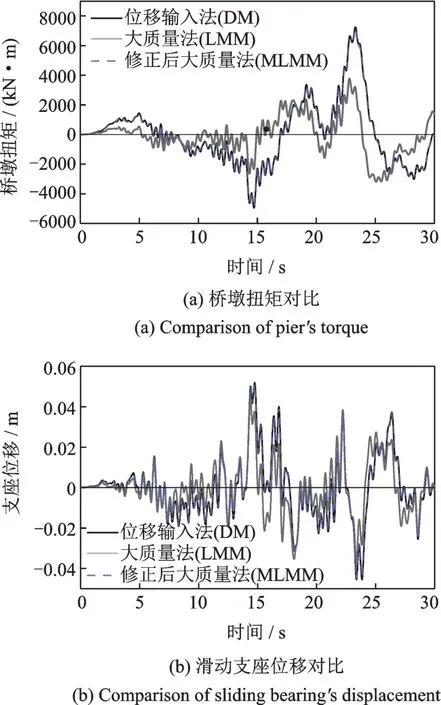
图1 不同输入方法的结果对比Fig.1 Comparison of results of different input methods
2 空间相关多点地震动模拟及输入方案
为了研究多点地震动输入下,控制不同支撑点的加速度/位移峰值对结构非线性响应的影响,本节将设计大跨结构的地震动输入方案,并模拟满足预定控制目标的空间相关多点地震动。
2.1 结构模型
本文设计的桥梁模型如图2所示,该模型为一座全长120 m的3跨连续梁混凝土直线桥(跨度为30 m+60 m+30 m)。桥的主梁为预应力箱型梁,桥墩为矩形独柱式混凝土墩,墩高均为10 m,墩顶分别布置固定盆式支座、单/双向活动盆式支座,主梁两端为连接路堤的桥台。主梁采用C50混凝土,桥墩采用C40混凝土。采用通用有限元软件CSIBridge进行桥梁建模与分析,主梁、桥墩均采用框架单元,墩底固接;双向活动支座和单向活动支座的活动方向采用橡胶隔震单元,固定支座采用线性弹簧单元,释放其他方向自由度。在有限元模型中,主梁属性设置为弹性;桥墩塑性铰的恢复力模型选用Takeda模型;活动支座的恢复力模型选用双线性模型,基本参数可由《公路桥梁抗震设计细则》[24]计算得到,如屈服强度为18.12 kN,屈服位移为0.005 m,屈服后刚度比设置为0。计算模型采用Rayleigh阻尼,阻尼比为5%,其中质量阻尼系数α=0.7778,刚度阻尼系数β=2.187×10-3;模型前三阶自振周期分别为0.71,0.50和0.47 s。
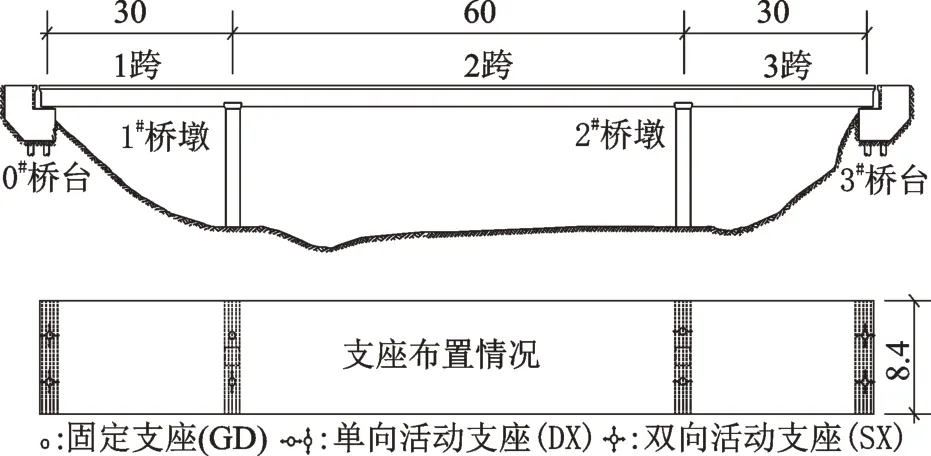
图2 桥梁模型(单位:m)Fig.2 Bridge model(Unit:m)
2.2 地震动输入方案及人工模拟
依据图2所示的桥梁模型,进行0#桥台(支点A)、1#桥墩(支点B)、2#桥墩(支点C)及3#桥台(支点D)横向的地震动拟合。为了综合考虑空间相关多点地震动的强度(频率)非平稳特性、不同峰值加速度/位移控制条件对桥梁结构非线性响应的影响,本文设计了两类(六组)多点地震动输入方案,如表1所示。
第一类地震动模拟时,引入具有统计参数的时-频包线函数[16],同时考虑加速度时程强度和频率非平稳特性,并分为三个方案,其中方案1-1控制4个支撑点的加速度峰值相同(相应的位移时程峰值随机),方案1-2按照4个支撑点位移时程峰值的最大值控制4条位移时程的峰值,方案1-3按照4个支撑点位移时程峰值的最小值控制4条位移时程的峰值。
第二类地震动模拟时,采用强度包线函数[25],仅考虑地震动强度非平稳特性,同样按照控制不同支撑点的加速度峰值相同或位移峰值相同设计了三个模拟方案,即方案2-1、方案2-2和方案2-3。
现按照表1所示的地震动模拟方案进行桥梁4个支撑点的地震动模拟。地震动模拟时,目标反应谱采用《建筑抗震设计规范》(GB 50011-2010)中的反应谱[26],其中地震动加速度峰值为0.102g,特征周期为0.4 s,曲线下降段的衰减指数为0.9,结构的阻尼比为0.05。地震动拟合时,取80个频率控制点确定目标反应谱,且对目标谱的允许拟合误差为5%。初始种子时程选取美国San Simeon地震P06台站的东西向(EW)地震加速度记录,并采用了基于San Simon地震台阵记录得到的相干模型[27]。

表1 多点地震动模拟方案Tab.1 Simulation schemes of multi-point ground motions
(1)第一类地震动模拟:表征地震动强度和频率非平稳特性。
方案1-1:根据种子时程的实际场地条件,选取主频率参数构建具有统计意义的时-频包线函数[28],则对应于采样频率fk处的时频联合分布函数为

式中主频率Fp(t)定义为一系列采样时间点t1,t2,…,tn对应于时频谱的最大幅值的频率值;强度包线采用三段式包线函数E(t),如下式所示
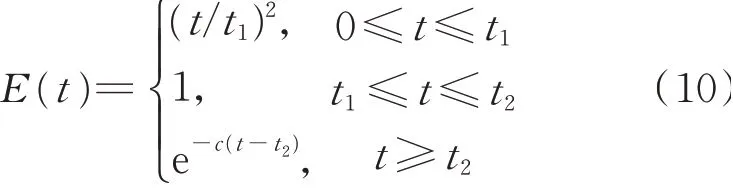
按照种子时程的5%到75%的Arais强度定义三段式包线函数,即t1=5 s,t2=13 s,c=0.347。则基于主频率构造的时-频包线函数可由下式表示

按照文献[28]建立的空间相关多点地震动拟合方法,拟合得到匹配反应谱、加速度峰值的4个支撑点地震加速度时程如图3所示。4条加速度时程的峰值均为0.102g,对目标反应谱的拟合误差均小于5%,且对地震动空间变化模拟效果较好。
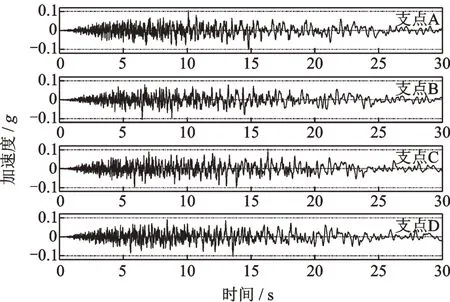
图3 空间相关多点加速度时程(方案1-1)Fig.3 Spatial correlation multi-point acceleration time history(Scheme 1-1)
方案1-2:对方案1-1拟合得到的4条加速度时程进行两次积分得到相应的4条位移时程,其位移峰值分别为0.104,0.135,0.0854和0.107 m,以位移峰值的最大值(0.135 m)作为位移峰值目标对4条位移时程进行调整,最终得到4条峰值均为0.135 m的位移时程,如图4所示。该组时程的其他控制条件,如反应谱、频率和强度非平稳特性、空间相关性等,均与方案1-1相同。

图4 空间相关多点位移时程(方案1-2)Fig.4 Spatial correlation multi-point displacement time history(Scheme 1-2)
方案1-3:以位移峰值的最小值(0.0854 m)作为位移峰值目标对4条位移时程进行调整,得到4条位移峰值均为0.0854 m的位移时程,如图5所示。同样,该组时程的其他控制条件与方案1-1相同。
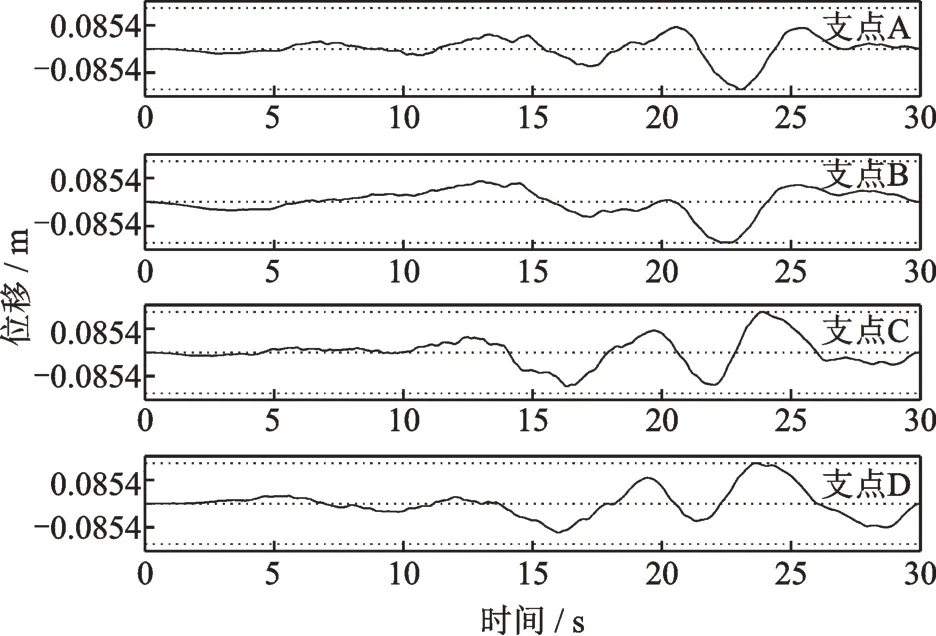
图5 空间相关多点位移时程(方案1-3)Fig.5 Spatial coherention multi-point displacement time history(Scheme 1-3)
(2)第二类地震动模拟:仅考虑了地震动强度非平稳特性。
方案2-1:采用三段式强度包络函数E(t)在时域内进行初始地震动调整,强度包线参数同方案1-1。按照预定的目标反应谱、加速度峰值、空间相关参数等,拟合得到4个支点的地震加速度时程,如图6所示。模拟得到的4条加速度时程的峰值均为0.102g,对目标反应谱的拟合误差均小于5%,且对地震动空间变化模拟效果较好。
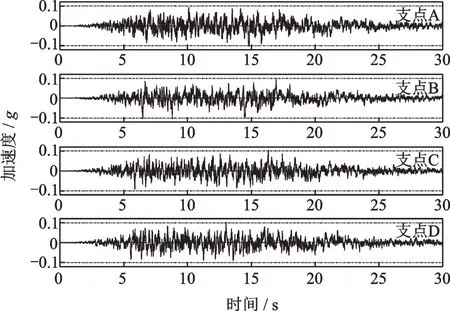
图6 空间相关多点加速度时程(方案2-1)Fig.6 Spatial coherention multi-point acceleration time history(Scheme 2-1)
方案2-2:对方案2-1拟合得到的4条加速度时程进行两次积分得到相应的4条位移时程,其位移峰值分别为0.0732,0.106,0.0776和0.0955 m,以位移峰值的最大值(0.106 m)作为位移峰值目标对4条位移时程进行调整,最终得到4条位移峰值均为0.1060 m的位移时程,如图7所示。该组时程的其他控制条件,如反应谱、强度非平稳特性、空间相关性等,均与方案2-1相同。

图7 空间相关多点位移时程(方案2-2)Fig.7 Spatial coherention multi-point displacement time history(Scheme 2-2)
方案2-3:以位移峰值的最小值(0.0732 m)作为位移峰值目标,对4条位移时程进行调整,最终得到4条位移峰值均为0.0732 m的位移时程,如图8所示。该组时程的其他控制条件(反应谱、强度非平稳特性、空间相关性)与方案2-1相同。
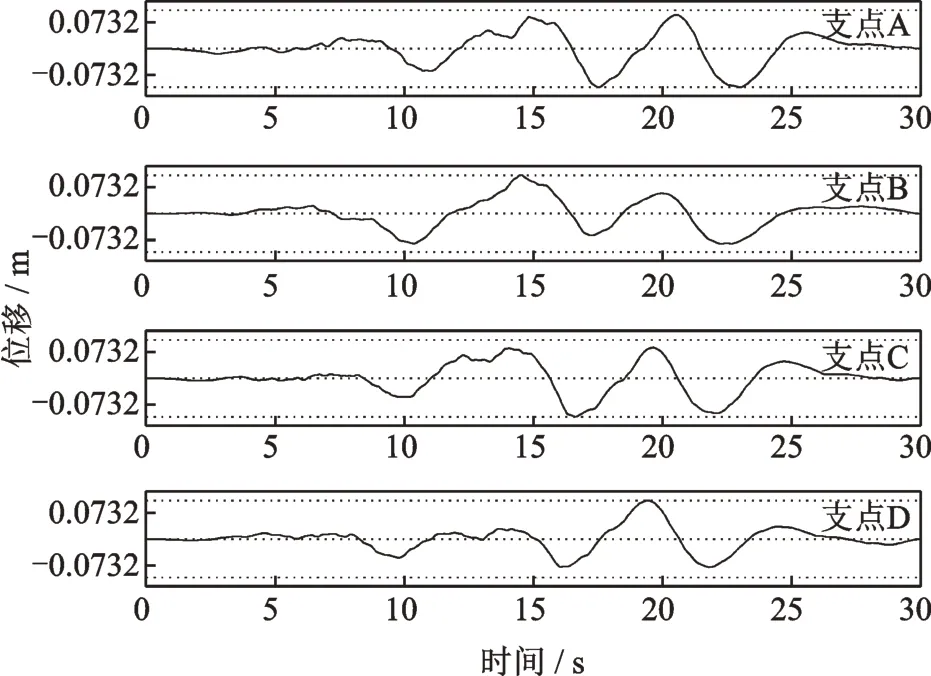
图8 空间相关多点位移时程(方案2-3)Fig.8 Spatial coherention multi-point displacement time history(Scheme 2-3)
3 关键拟合参数对结构非线性响应的影响
将拟合得到的6组空间相关多点地震动,采用多点输入的方式对图2所示的结构进行非线性反应分析,可得到桥墩和主梁的内力、位移等响应参数。表2给出了6组输入方案计算得到的桥墩的剪力和扭矩;表3为3跨主梁的跨中弯矩;表4为桥墩和主梁的横向位移。本节将分析采用不同输入方案时结构响应的变化,来说明地震动特性及不同加速度/位移峰值控制条件对结构响应的影响。
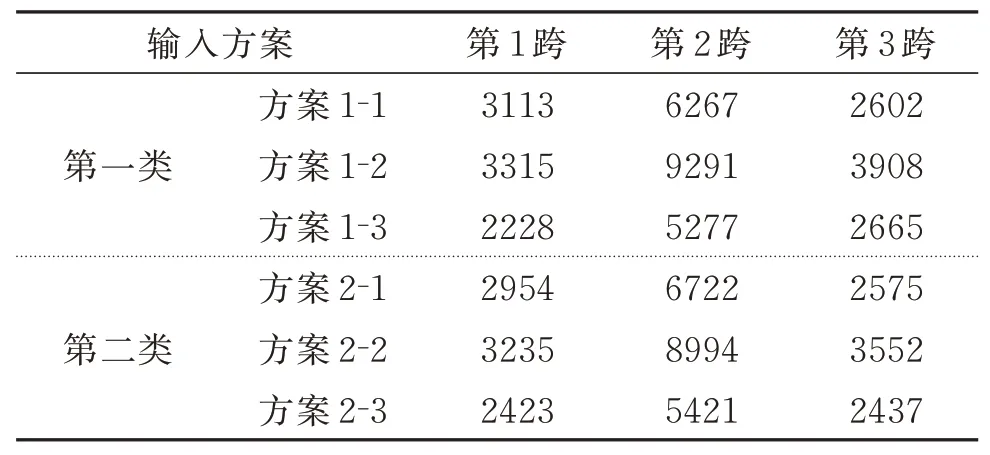
表3 不同输入方案主梁跨中弯矩对比/(kN·m)Tab.3 Comparison of mid-span bending moment of main girders with different input schemes/(kN·m)
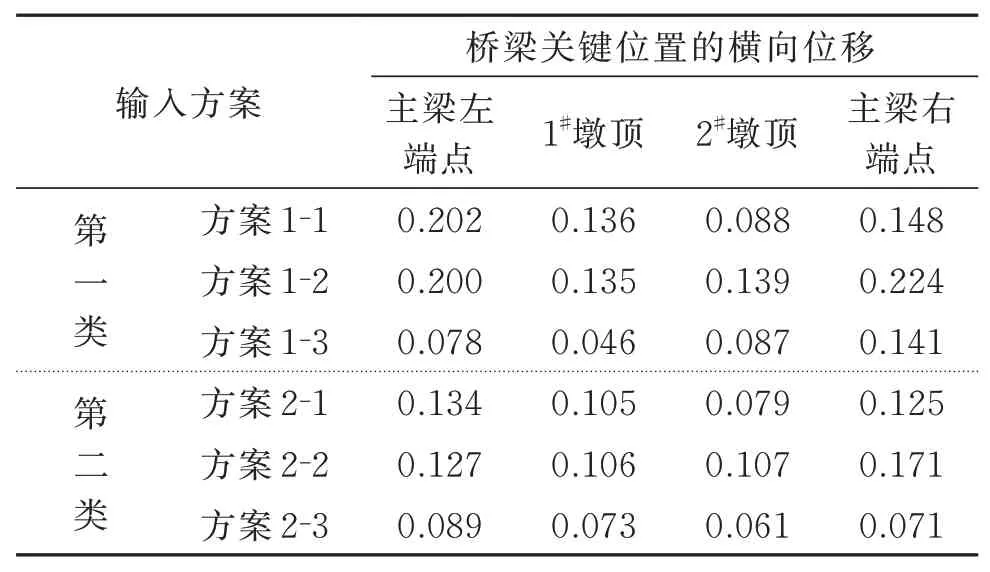
表4 不同输入方案桥梁横向位移/mTab.4 Lateral displacements of bridge with different input schemes/m
桥墩屈服时对应的等效屈服剪力为1560 kN,超过这个值桥墩将进入非线性,表2中的数据表明,2#桥墩在方案1-2和方案2-2中均已率先屈服,进入了非线性,恢复力曲线如图9所示。表明控制位移峰值的大小将会影响桥梁结构进入非线性程度的强弱,当按照最大位移峰值进行控制时,桥墩率先进入了非线性,滞回环的耗能面积开始增加,相应的桥墩内力及位移响应量增大。图10给出了3#桥台的支座在第一类输入方案下的恢复力曲线,可以看出在3种输入方案下支座均已进入非线性,并且支座在方案1-2中的滞回耗能面积和位移峰值要明显大于方案1-1和方案1-3的结果;图11进一步给出了两类不同输入方案下支座滞回耗能面积的对比,可以看出,当按照最大位移峰值进行控制时(方案1-2和方案2-2),支座的滞回耗能面积更大,因而结构进入的非线性程度更深,相应的桥梁横向位移也将增大。

图9 2#桥墩的恢复力曲线Fig.9 Restoring force curves of 2# pier
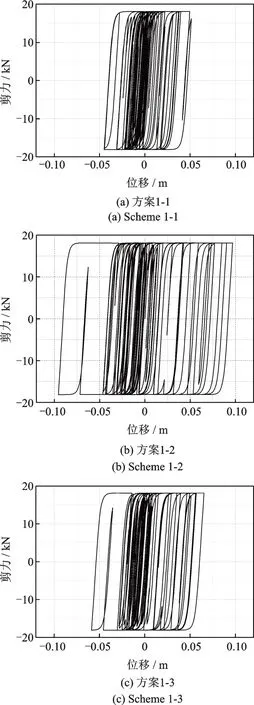
图10 不同方案下3#桥台支座恢复力曲线对比Fig.10 Comparison of restoring force curves of bearings in 3# abutment under different schemes
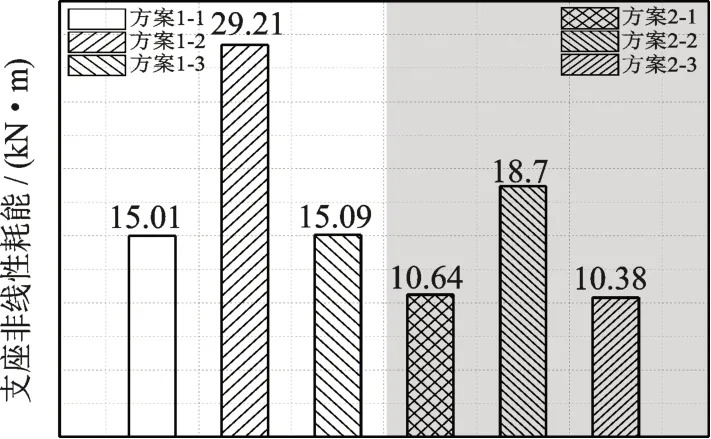
图11 3#桥台支座的非线性耗能对比Fig.11 Comparison of nonlinear energy dissipation of bearings in 3# abutment

表2 不同输入方案桥墩的剪力和扭矩对比Tab.2 Comparison of shear force and torque of bridge piers with different input schemes
因此以下将分别对桥梁的内力和位移响应情况进行讨论,分析空间相关多点地震动的位移峰值控制对结构非线性响应的影响。
3.1 控制不同的位移峰值对结构响应的影响
3.1.1 对内力的影响
基于表2和表3中的结果,首先计算了结构在方案1-2和方案1-3输入下的内力响应相对于方案1-1输入下结构响应的相对误差,其结果如图12(a)所示。分析误差变化可以看出,当按照最大的位移峰值进行位移时程的控制时(方案1-2),桥墩的剪力和扭矩、主梁跨中弯矩大都会得到相对较大的结果,相应于各参数的最大增幅分别约为25%,21%和50%;若按照最小的位移峰值进行位移时程的控制时(方案1-3),无论是桥墩的剪力和扭矩,还是主梁的跨中弯矩,与方案1-1的计算结果相比,减小的幅度较大,相对于各参数最大降低幅度分别约为37%,26%和28%。在方案2-2和方案2-3输入下的结构响应相对于方案2-1输入下计算结果的相对误差如图12(b)所示。同样地,当按照最大位移进行控制时(方案2-2),也得到相对较大的结构响应,各参数的最大增幅分别为17%,25%和38%;若按照最小的峰值位移进行控制,计算得到的桥墩剪力和扭矩、跨中主梁弯矩的最大减小幅度分别为30%,18%和20%。

图12 不同地震动输入方案桥梁内力变化Fig.12 Internal force changes of bridge in different ground motion input schemes
由以上分析可以看出,按照位移输入法进行结构分析时,控制位移峰值的大小对结构内力响应有较大的影响,但是这种影响似乎与位移时程的形状无明显的相关性,如图13所示的主梁跨中弯矩的变化来看,虽然方案1-2和方案2-2的位移时程来自不同的地震动特性分组,且形状不同,但由于位移峰值(PGD,Peak Ground Motion Displacement)较大,都得到了相对较大的计算结果,而且大部分的内力结果都是随着峰值位移的减小逐渐减小。分析表2中的结构响应,这种变化也同样出现在桥墩的扭矩和剪力的结果中,进一步说明位移输入法中各支撑点处地震动的位移峰值与结构的内力响应之间呈现正相关。由于在以加速度反应谱和加速度峰值为目标的地震动拟合中,不同支撑点处位移的峰值离散性比较大,所以为了保证结构的安全,地震动拟合中应控制位移峰值的最小取值。
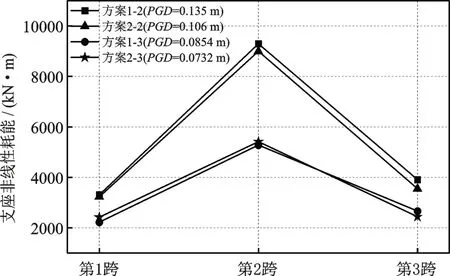
图13 地震位移输入方案下主梁跨中弯矩情况Fig.13 The mid-span bending moment of the main girders under the seismic displacement input schemes
3.1.2 对横向位移的影响
分析表4的数据,发现采用加速度输入(方案1-1)和位移输入(方案1-2)时,计算得到的2#墩顶的位移响应出现了不同的变化规律,即当采用加速度输入时,其位移响应比1#墩顶位移减少约35%,但当采用位移输入时,两个墩顶得到位移响应相当。产生这种情况的原因可能有两个,其一是加速度输入时对应于2#桥墩的位移峰值是4个支点中的最小值,故方案1-2中对其调整的幅度最大;其二是2#墩顶设置了纵向滑动支座,相对于1#墩顶的固定支座,滑动支座可能对位移输入的峰值变化更加敏感。第二类方案中的结果也与之类似。
图14给出了采用不同地震动输入方案时,桥梁关键位置横向位移相对于方案1-1和方案2-1计算结果的相对误差变化。从图14(a)可以看出,当控制位移输入峰值为最大值时(方案1-2),与方案1-1的结果相比,2#墩顶的位移增幅达到56%,主梁右端的横向位移增幅也达到47%;此外,如果按照较小的峰值位移进行4个支点的位移控制,一般会得到相对较小的位移结果,减小幅值达66%。图14(b)所示的第二类地震动输入方案也计算得到了类似的结果。综合分析两类(6组)地震动输入下结构的位移响应可以看出,控制不同的位移峰值条件得到的位移响应的变化和结构内力响应变化基本一致,这进一步说明地震位移输入峰值的控制对结构的位移响应有较大的影响,当采用位移输入法进行计算时,应该合理控制输入时程的位移峰值。
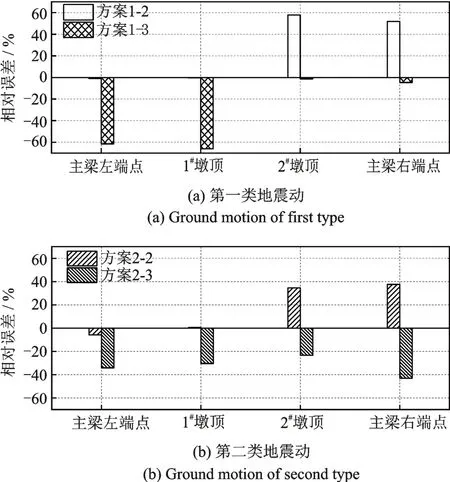
图14 不同地震动输入方案桥梁横向位移变化Fig.14 Lateral displacement changes of bridge in different ground motion input schemes
3.2 地震动频率非平稳特性对结构响应的影响
本文在4个支撑点的相关加速度时程模拟中,采用时-频包线函数模拟地震动频率和强度非平稳特性(方案1-1),采用强度包线函数模拟地震动强度非平稳特性(方案2-1)。虽然方案1-2、方案1-3、方案2-2和方案2-3是加速度时程的位移时程,但拟合方案中按不同的位移峰值进行了调整,因此本节仅比较控制了相同加速度峰值的方案1-1和方案2-1的计算结果,来说明频率非平稳特性对结构响应的影响。
3.2.1 对内力的影响
为了直观地分析地震动频率非平稳特性对结构内力响应的影响,图15给出了采用方案1-1和方案1-2地震动输入时计算得到的桥墩剪力、扭矩及主梁的跨中弯矩。可以看出,若考虑输入地震动的频率非平稳特性,1#桥墩的剪力和扭矩、2#桥墩的扭矩都得到相对较大的值,与仅考虑地震动强度非平稳特性(方案2-1)的计算结果相比最大的增幅达到了63%。比较3跨主梁的跨中弯矩可以发现,虽然方案1-1计算得到的第1和第3跨的跨中弯矩与方案2-1的结果相比略有增加,但增加的幅度不大。由以上的分析可以看出,地震动输入特性对主梁的跨中弯矩、桥墩剪力的影响不明显,但对桥墩扭矩的影响比较显著。总体来看,若地震动拟合中不考虑频率的非平稳特性,则存在低估结构内力响应的风险。
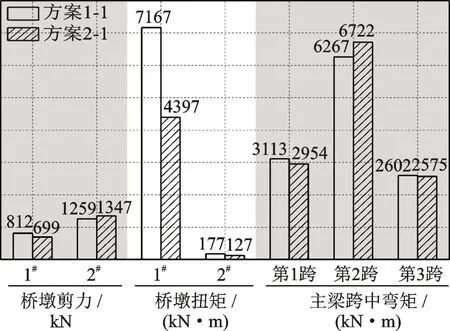
图15 方案1-1和方案2-1计算得到的桥梁内力Fig.15 Internal forces of bridge in schemes 1-1 and 2-1
3.2.2 对横向位移的影响
图16直观地给出了两种输入方案下,计算得到的桥梁4个关键位置的横向位移。相较于内力的变化,地震动特性变化对位移响应的影响比较明显,采用考虑频率非平稳特性的加速度输入都会得到相对较大的位移响应,与方案2-1输入时计算得到的位移响应相比,最大的增幅达到了50%。这些结果进一步说明,在空间相关多点地震动拟合中,应该合理地考虑地震动的频率非平稳变化特性。
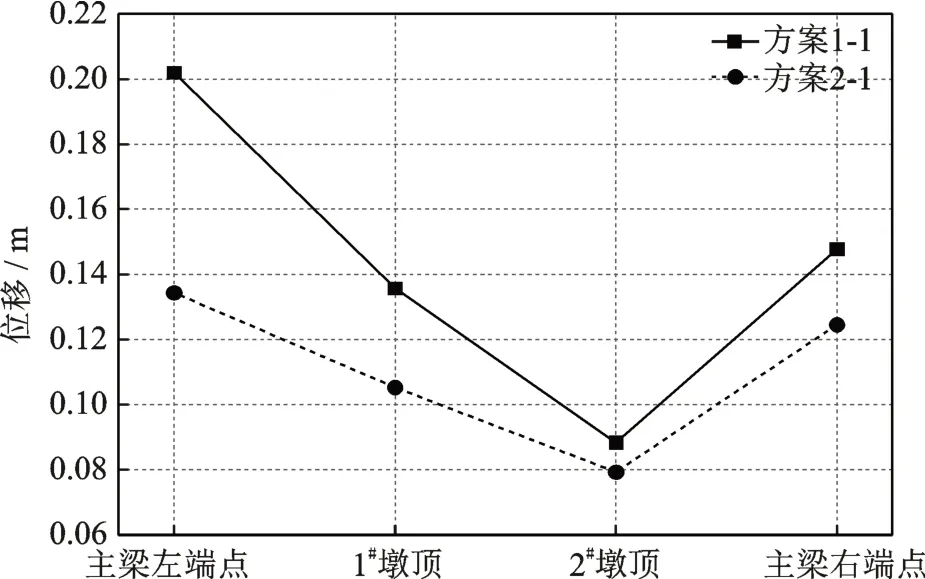
图16 方案1-1和方案2-1计算得到的桥梁横向位移Fig.16 Lateral displacements of bridge in schemes 1-1 and 2-1
4 结论
本文通过引入不同的包线函数和控制不同的加速度/位移峰值目标,合成了能够反映空间相关地震动非平稳特性和峰值控制的两类(6组)多点地震动,对大跨桥梁进行非线性时程分析,得出以下主要结论:
(1)控制地震位移时程的峰值对结构内力和位移响应有较大的影响,输入位移时程峰值越大,结构进入非线性的程度越深,得到的结构响应越大,且与位移时程的形状无明显相关性;
(2)以加速度反应谱和加速度峰值为目标的空间相关地震动拟合中,各支撑点处位移时程的峰值离散性比较大,为了保证结构的安全,空间相关多点地震动拟合中应控制位移峰值的最小取值;
(3)地震动的频率非平稳特性对桥梁的位移响应、桥墩扭矩影响明显,对主梁内力、桥墩剪力影响较小;但如果仅考虑地震动强度非平稳特性,则存在低估结构响应的风险。
因此,在实际工程应用中计算大跨桥梁结构的非线性时程响应时,不仅需要合理地描述地震动的空间变化特性,还需要考虑地震动频率的非平稳特性,同时控制位移输入的最小峰值,从而合理估计结构的地震响应,进而保证结构抗震设计的安全性。
