边界摩擦条件下含有预紧的对合碟簧隔振单元振动与稳定性分析

2022-01-12惠安民孙自强张晓友王开平刘海超

振动工程学报 2021年6期

闫明，惠安民，孙自强，张晓友，王开平，刘海超

（沈阳工业大学机械工程学院，辽宁沈阳110870）

引言

碟型弹簧（简称碟簧）是一种具有良好非线性刚度特性的金属弹簧，具有体积小、加载均匀、承载能力高、自阻尼等优点［1-2］。可以根据不同工作条件将多片碟簧以不同叠放方式，组成具有不同的非线性刚度与复合阻尼特征的弹性元件［3-4］。因此，在各个领域都得到了较为广泛的关注与研究。

基于碟簧本身力学性能研究，Almen等［5］、Rosa等［6］、Saini等［7］分别对等截面碟簧、线性变化截面碟簧与抛物线型变化截面碟簧的承载能力与轴向变形进行了理论推导，并分别建立了不同截面变化的碟簧的载荷大小与变形的公式。与此同时，Almen等［5］还在文中提出了碟簧对合放置时，其内部结构间的Coulomb阻尼系数最小的观点；OZAKI等［8］通过数值计算方法对碟簧在考虑摩擦时的静态与动态刚度特性进行计算；ZHENG等［9］针对大变形的碟簧提出了能量法求解其载荷与挠度的解析解，该解比传统公式具有更高的精度；Ye等［10］基于梁与锥壳的有限旋转与大挠度理论，对不同形式的异形开槽碟簧进行了力学分析，并提出一种试验方法，详细研究了碟簧应变与应力的分布规律，指出了传统计算中的不合理假设。而在振动控制领域，Jia等［11］建立了高速压力机用组合碟簧隔振装置，对其加载与卸载过程进行了理论分析，并通过试验确定了最佳碟簧组合，但并未讨论其振动特性；Xu等［12］同样基于组合碟簧，设计了一种隔振耗能装置，并对其阻尼特性进行了理论分析与试验探究，结果显示其具有良好的耗能与自定心特性；高跃飞等［13］在对火炮系统的缓冲控制进行研究时，选用碟簧作为弹性缓冲元件，并对该碟簧缓冲系统的冲击刚度进行了建模与试验研究；王维等［14］研究了碟型弹簧竖向隔振装置力学特性，建立并分析了该隔振装置的恢复力模型与受力机理，并对其在基于往复载荷作用下的滞回曲线与耗能能力进行了试验分析，得到了该碟簧隔振装置的等效刚度与等效阻尼；工程上一般在设计碟簧隔振器时，为了简化设计步骤，均将其等效为线性阻尼或线性刚度的隔振系统［15-17］。但由于碟簧叠合方式的不同以及系统内碟簧数目的增大，各碟簧结合面间的边界摩擦效应与刚度非线性特性变得越来越明显，这导致了线性模型无法准确表述隔振系统的振动特性。

综上所述，目前对于单片碟簧的刚度特性，考虑摩擦条件下的准静力学特性已有了较为丰富的试验研究和理论成果。而对于组合类碟簧和组合类碟簧隔振装置的研究多集中在阻尼特性或等效线性化后的振动特性上，鲜有文献针对对合碟簧隔振装置的非线性振动特性，特别是振动稳定性进行研究，而系统的振动稳定性往往是衡量隔振系统优劣的重要特性之一。因此，本文根据实际工程背景，提出了一种含有预紧的对合碟簧隔振单元，建立并推导其非线性振动微分方程，并对其振动特性以及振动稳定性进行分析与讨论。

1 考虑边界摩擦与预紧的碟簧隔振单元

1.1 碟簧隔振单元

基于实际工程需求，设计了一种碟簧隔振单元，如图1所示为其结构原理图。该隔振单元的结构特点为：弹性元件由多组对合碟簧组串联布置而成，且每对对合碟簧的接触面处均布置有平垫圈，以保证隔振单元在拉压运动过程中受力均匀。根据不同工作需求，可以调节隔振单元中碟簧压板的厚度，以改变隔振单元中的预紧力大小。碟簧压板1#与2#之间充入适当硅油进行润滑。

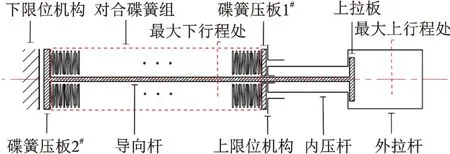
图1 碟簧隔振单元原理图Fig.1 Schematic diagram of disc spring vibration isolation unit

该碟簧隔振单元受载后的运动方式为：腔体中含有预紧的对合碟簧组被向下运动的内压杆以及碟簧压板1#压缩至下行程最大处，然后系统在对合碟簧组的弹性力作用下，返回至初始静平衡位置；或在惯性力与简谐力作用下，腔内对合碟簧组被向上运动的外拉杆、上拉板以及碟簧压板2#压缩至上行程最大处，同样在对合碟簧组的弹性力作用下，系统返回至初始静平衡位置，完成单次运动，系统会按照上述规律周期性运动，直至外界激励传递给系统的能量通过对合碟簧中存在的阻尼耗尽为止。该结构显著优点为：可以将外界传递给隔振单元的轴向拉、压力全部转化为对对合碟簧组的轴压力，在保证系统结构紧凑的同时也保证了对合碟簧组间预紧力恒存在。

如图2所示，为上述碟簧隔振单元中的一对对合碟簧组的剖视图，对合碟簧组由一对对合放置的碟簧和平垫片组成。碟簧为A系列无支撑碟型弹簧，其材质为60Si2Mn。中间垫片主要作用为：使碟簧受力均匀，保证系统稳定，防止碟簧压缩过程中出现卡死现象，与此同时，在碟簧与平垫片的接触圆上存在边界摩擦效应，可为碟簧隔振器提供阻尼。图中：D和d分别为碟簧的外径和内径；t为碟簧的厚度；h0为碟片的最大压缩量；H0为碟片的自由高度。

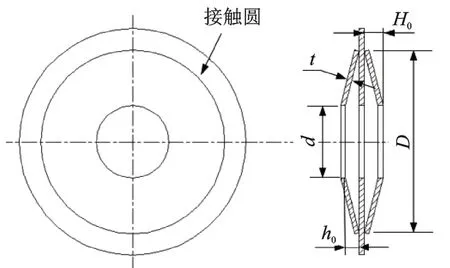
图2 对合碟簧组Fig.2 Opposed disc spring unit

1.2 碟簧隔振单元的非线性振动模型

根据GB/T 1972-2005《碟型弹簧》［18］规范中单个碟簧的力与挠度计算公式

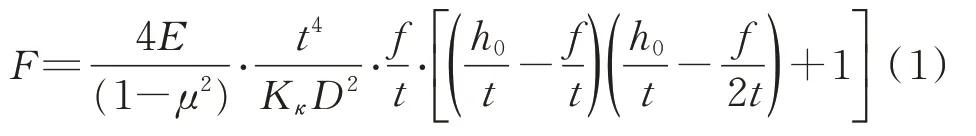
考虑边界摩擦与预紧力条件下的对合碟簧隔振单元，其刚度曲线可由轴向位移x的三次函数所表达，文献［19］详细叙述了该碟簧隔振单元刚度模型的建立过程，其刚度可表达为

式中K1，K2，K3分别为非线性刚度的一次、二次与三次项系数；α为碟簧隔振器初始预紧力；F为弹性恢复力；xs为碟簧预压缩位移；且有基于此可知，除碟簧材料参数外，在隔振系统中，碟簧厚度t越大，碟簧自由高度H0越高，碟簧个数n越少，碟簧外径D值越小，Kκ值越小，则系统的三次项刚度系数就越大，系统表现出的非线性特性就越明显，通过调节以上碟簧几何参数的配比即可以获得不同的刚度特性。

与此同时，系统运动过程中，碟簧在接触圆上存在边界摩擦效应，该边界摩擦效应可应用Coulomb阻尼进行描述。而Coulomb阻尼对系统轴向提供了附加支持力ΔFn，该附加支持力ΔFn的方向与系统的速度方向相反［16］。因此可以应用符号函数对其进行描述，建立变刚度的碟簧-质量系统模型，其隔振原理图如图3所示。

图中：M为系统承载质量（其自身重力大于等于系统预紧力）；c为系统黏性阻尼系数；Kt为系统非线性刚度，其刚度变化规律符合式（1）。系统加载后，其平衡位置改变量为x0。x，y分别为隔振系统中承载质量M和基础的绝对位移量。ÿ为基础所受简谐激励的绝对加速度值。

令承载M的总绝对位移量为χ=x+x0，则根据式（2）该碟簧-质量隔振系统在基础激励下的运动微分方程为：

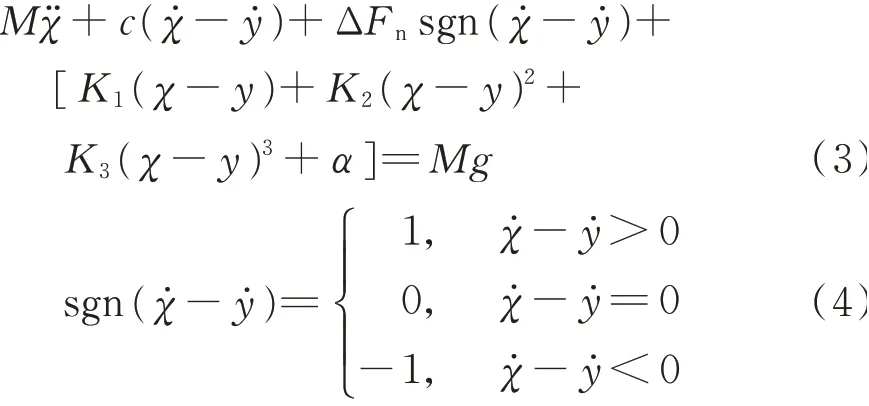
式中“·”代表对时间的导数，令λ=χ-y并带回方程（3）与（4）中，经整理可得：

设非线性方程在Ω=1的主共振区域附近，其响应为

式中振幅A（τ）与相位θ（τ）为随时间的周期慢变函数。即为无穷小量。根据Klotter［20］提出的对上述微分方程的求解方法，可用下式计算出其幅频特性方程

式中A0为函数A（τ）的最大值，ψ为虚拟积分变量。整理式（9）可得，系统的幅频特性方程为

由幅频特性方程（10）可知，该系统振动幅值A0仅与非线性刚度的三次无量纲项系数α2、黏性阻尼的无量纲系数μ1以及附加支持力的无量纲系数μ2有关，与非线性刚度的二次项无量纲系数α1无关。

2 碟簧隔振单元周期解的稳定性分析

为进一步讨论周期解σ（τ）=A（τ）·cos［Ωτθ（τ）］的稳定性，现将sgn(σ̇)展开成Fourier级数形式

式中省略部分表示高次谐波项。根据谐波平衡法，将式（7）与（10）代回至方程（6）中，并略去Ä(τ)的同阶与高阶无穷小项以及sgn(σ̇)项中的高次谐波项，根据等式两边对应一次谐波的系数相等，整理可得

令式（12）中的慢变函数近似等于常数，即令A（τ）=A0，θ（τ）=θ0，并代回至方程（12）中，可得方程

由此，根据三角函数的性质，可同样计算得到幅频特性方程式（10）。这也验证了应用Klotter求解方法求解该非线性振动方程的正确性。

引入微扰动量ε，κ（ε，κ均趋近于0），并满足

将微扰动方程（14）代入式（12）中，可得

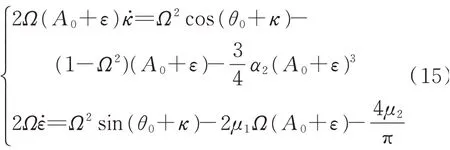
由于ε，κ趋近于零，ε̇和κ̇为其高阶无穷小量，故可以认为下式满足精度要求

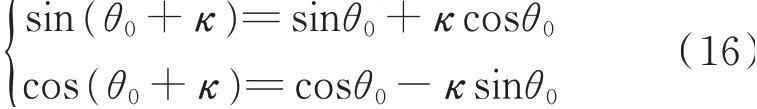
对式（15）中的三角函数按照式（16）中的形式进行展开，并考虑式（13）的关系，对展开式进行整理，略去ε⋅κ̇以及其同阶的无穷小量，得到系统扰动方程

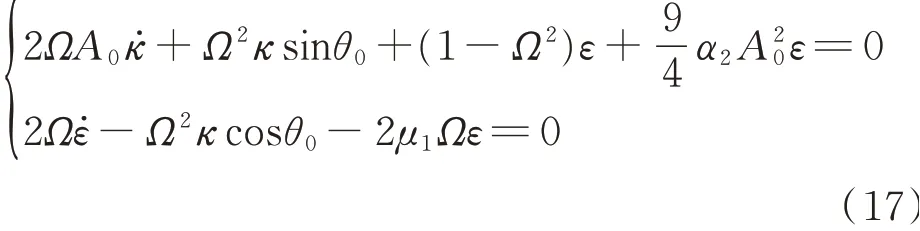
设扰动方程的解为：ε=ε0est，κ=κ0est，将其代回至扰动方程（17）中，可得其解的特征方程式为

求解特征方程（18），并同时考虑式（13）中各变量间的关系，整理后可得

由此，基于Routh-Hurwitz系统稳定性判定条件，可解得该周期解的稳定区间为

3 系统参数对隔振单元振动特性及其振动稳定性的影响

由碟簧间的边界摩擦效应引起的Coulomb阻尼力，其值的大小主要取决于碟簧接触圆上的正压力与系统摩擦系数μe，而Coulomb阻尼力是引起附加支持力的关键因素。根据计算，可得到单片碟簧在不同摩擦系数条件下，其轴向压缩距离与附加支持力ΔFn的关系曲线，如图4所示，其具体计算与推导过程，可参看文献［19］。其中碟簧的几何参数为：t=0.5 mm，D=28 mm，d=10 mm，H0=1.15 mm，h0=0.7 mm；根据边界摩擦润滑条件［21］，系统摩擦系数范围为0.1-0.3，因此此处摩擦系数μe分别选取0.1，0.2和0.3。

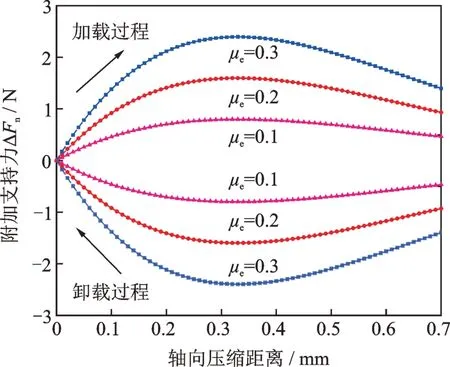
图4 碟簧加载过程轴向压缩距离与附加支持力关系曲线Fig.4 Relationship between axial compression distance and additional supporting force during disc spring loading

由此可知，对合碟簧隔振单元的附加支撑力无量纲系数μ2与其轴向位移在一定范围内呈正相关。在该范围内，为简化计算难度，规定两种振动状态，即：小位移条件下的受迫振动状态与大位移条件下的受迫振动状态。为进一步研究系统中各参数对其振动以及稳定区间的影响，分别选取两种振动状态下的系统参数进行求解，具体分析过程如下。

3.1 小位移条件下的受迫振动

由图4可知，当隔振系统的轴向位移量很小时，即使系统内存在较大的摩擦系数，但系统中的附加支持力ΔFn仍然很小。为探究Coulomb阻尼所引起的附加支持力ΔFn对系统的影响，选用较小的附加支持力无量纲系数μ2，并对上述幅频特性方程（10）与其对应的稳定区间进行求解，如图5所示。

图5 小位移条件下附加支持力系数μ2对幅频特性曲线与稳定区间的影响Fig.5 The influence of additional supporting force coefficient μ2 on the amplitude frequency characteristic curve and the stable region

由图5可知，当系统中附加支持力无量纲系数μ2=0时，系统中仅存在黏性阻尼，此时系统为线性阻尼的非线性刚度隔振系统。而随着附加支持力无量纲系数μ2的出现并增大，系统共振峰值略有减小。且出现一种自锁现象，即：系统存在一个脱离频率Ωb，当激励频率Ω的值小于脱离频率Ωb时，此时A0=0，即承载质量M与基础间的相对位移为零，隔振器无隔振作用，承载质量M与基础间相当于刚性连接。为使幅频特性方程（9）恒成立，当A0=0时，必存在

即脱离频率Ωb与黏性阻尼无量纲系数μ1无关，但其平方与附加支持力无量纲系数μ2成正比。且随着附加支持力无量纲系数μ2值的增大，系统的不稳定区间向高频大振幅方向收缩，不稳定区间范围变小。

如图6（a）-（d）所示为小位移条件下，非线性刚度三次项无量纲系数α2对系统幅频特性曲线与稳定区间的影响，其中选取参数：μ1=0.2，μ2=0.05。由图可以看出，随着非线性刚度三次项无量纲系数α2的增大，系统幅频特性曲线中的共振区间逐渐变宽，共振峰值逐渐变大且向高频方向移动，当系数α2足够大时，系统出现跳跃现象。其上跳跃点（D点）与下跳跃点（B点）皆随系数α2的增大逐渐向高频方向移动。故非线性刚度三次项无量纲系数α2不宜选取过大，否则会加剧系统的共振现象与共振频宽，不利于设备的振动防护。

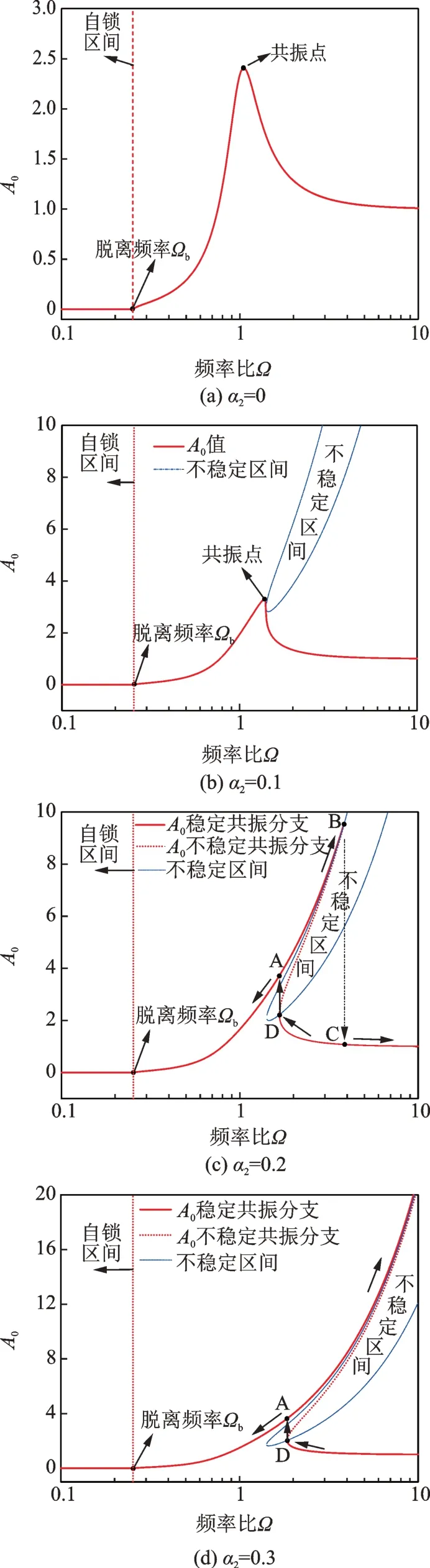
图6 小位移条件下非线性刚度三次项无量纲系数α2对幅频特性曲线与稳定区间的影响Fig.6 The influence of dimensionless coefficient of cubic term of nonlinear stiffness α2 on the amplitude frequency characteristic curve and the stable region

3.2 大位移条件下的受迫振动

随着轴向运动距离的增大，系统中由Coulomb阻尼所引起的附加支持力ΔFn也随之增大，为探究较大的附加支持力无量纲系数μ2对系统振动特性以及振动稳定性的影响；同样，首先选取非线性刚度三次项无量纲系数α2=0.2、黏性阻尼无量纲系数μ1=0，如图7（a）-（d）所示，分别为附加支持力无量纲系数μ2为0.1，0.5，1.3以及1.5求解得到的幅频特性曲线与稳定区间图。

如图7所示，由式（21）可知系统的脱离频率Ωb会随着附加支持力无量纲系数μ2的增大而逐渐向高频方向移动，其自锁区间的频宽会逐渐增大，当其值持续增大到如图7（c）所示的位置时，系统发生了较为异常的跳跃现象，即当基础的激励频率持续增大至H点对应频率时，系统相对位移的振幅A0发生一次阶跃增大现象，由H点直接跳跃至E点后，再沿稳定共振分支EA方向继续增大至共振下跳跃点B，最后通过下跳跃点B，跳跃回稳定分支DC段，此时系统共振阶段结束；而当基础的激励频率由大持续减小时，系统相对位移的振幅A0随激励频率减小至D点时，产生阶跃现象，振幅A0的值由D点直接跃升至A点后，沿稳定共振分支行至F处，产生第二次阶跃现象，由F点向下跳跃至G点，结束共振阶段。当继续增大附加支持力无量纲系数μ2的值，使其G点与脱离频率点Ωb重合，系统的幅频特性曲线呈现出如图7（d）的形式，该状态下，虽然系统仍然存在稳定的共振分支，但不再发生跳跃现象［22］，即激励频率达到系统脱离频率后，振幅A0按照较低的分支进行振动，此时系统不会发生或仅发生极其微弱的共振现象。

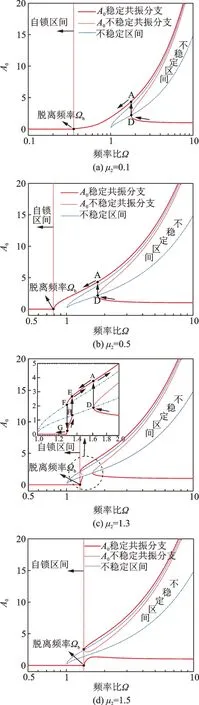
图7 大位移条件下附加支持力无量纲系数μ2对幅频特性曲线与稳定区间的影响Fig.7 The influence of dimensionless coefficient of additional supporting force μ2 on the amplitude frequency characteristic curve and the stable region

为进一步研究黏性阻尼无量纲系数μ1对该隔振系统幅频特性曲线与稳定区间的影响，选取非线性刚度三次项无量纲系数α2=0.2，并按表1中相关参数进行计算。

表1 相关计算参数Tab.1 Related parameters

如图8（a）-（d）所示，分别为表1中对应的参数计算得到的幅频特性曲线与稳定区间。由图8（a）可以很明显地观察到，仅当黏性阻尼无量纲系数μ1较小时，系统的幅频特性曲线随系数μ2的增大而出现异常跳跃情况与不向稳定共振分支跳跃的微共振或无共振情况。且出现这两种情况所需的μ2值会随着μ1的增大而逐渐减小，而其不稳定区间同样会随着系统参数μ2的增大向高频方向回缩；当黏性阻尼无量纲系数μ1继续增大时，由于其不稳定区间向高频回缩，此时系统不再发生异常跳跃情况，如图8（b）所示，但在该状态下，系统最终还会出现不向稳定共振分支跳跃的微共振或无共振情况；当黏性阻尼无量纲系数μ1继续增大时，如图8（c）-（d）所示，由于系统的共振峰值点会随着阻尼的持续增大而不再与不稳定区间有交集，此后系统将不再发生跳跃现象。

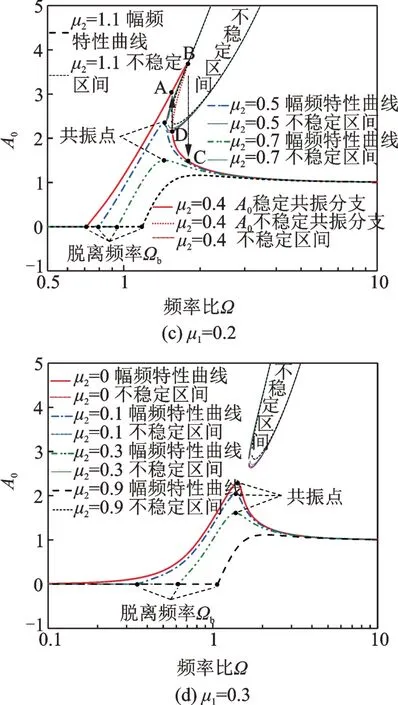
图8 大位移条件下黏性阻尼系数μ1对幅频特性曲线与稳定区间的影响Fig.8 The influence of viscous damping coefficient μ1 on the amplitude frequency characteristic curve and the stable region

4 隔振器定频试验及其结果分析

为验证上述计算规律的正确性，对含有多组对合碟簧单元的隔振单元样机进行如下定频试验并与计算数据进行对比。其中：碟簧片几何参数选取为：t=0.5 mm，D=28 mm，d=10 mm，H0=1.15 mm，h0=0.7 mm；对合碟簧组个数为25组、预紧力为40 N。

在定频试验前，为准确得到碟簧隔振单元样机的固有频率，首先对该隔振器在其额定承载质量4.6 kg条件下的自由衰减振动的相对位移与绝对加速度信号进行测量，并对测量得到的时域曲线进行傅里叶变换。如图9所示为自由振动条件下碟簧隔振单元经位移以及加速度时域信号得到的FFT谱图。

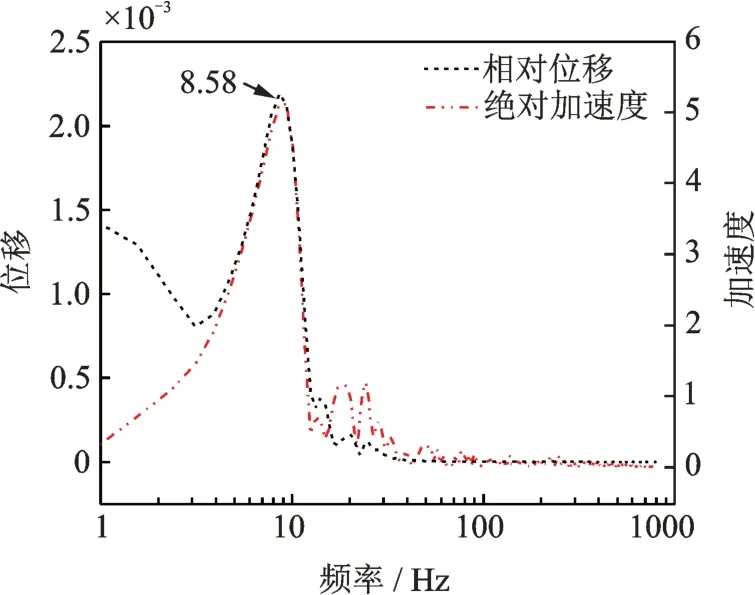
图9 碟簧隔振单元自由振动条件下的FFT谱Fig.9 FFT spectrum of disc spring vibration isolation unit under free vibration condition

由相对位移与绝对加速度的FFT谱可知，系统固有频率取8.58 Hz为宜。基于此，展开定频试验，其定频试验的测试频率区间为：2-40 Hz，其中2-20 Hz频率段，每2 Hz选取一个采样点；20-40 Hz频率段，每10 Hz选取一采样点。为保证定频试验得到测量数据的稳定与准确性，每组定频试验的振动持续时间设为1 min。如图10所示为对合碟簧隔振单元样机定频试验图。

图10 对合碟簧隔振单元样机定频试验Fig.10 Fixed frequency test of prototype of vibration isolation unit with opposed disc spring

图10中振动试验台上放置有B&K4384压电式加速度传感器，用以监控实验台的振动情况。振动试验台由ECON公司生产的液压振动试验机，其最大推力为100 kN，振动频率范围为0.1-200 Hz。采用ECON公司生产的MI7016型16通道数据采集仪进行数据采集，采用MTS公司生产的CS系列磁致非接触型位移传感器对配重与试验台面间的相对位移时域信号进行测量，试验台面的绝对位移时域信号由振动试验台本身的位移传感器提供。如图11所示，分别为不同激励频率条件下，激励的绝对位移时域曲线与隔振系统响应的相对位移曲线（此处仅给出典型位移的时域曲线）。

图11中由于激励的绝对位移时域曲线是由振动试验台内部位移传感器测量并提供，响应的相对位移时域曲线由MI7016型数据采集仪提供，而本试验主要关注的是位移幅值，因此为简化数据处理过程，图中不包含以上两个位移时域曲线的相位信息。基于以上定频试验的试验数据与隔振单元本身固有频率信息，可得隔振系统的幅频特性曲线如图12所示。

图11 激励的绝对位移与响应的相对位移时域曲线Fig.11 Time domain curve of absolute displacement of excitation and relative displacement of response

由图12（a）的试验幅频特性响应曲线与理论幅频特性响应曲线对比可知，两者吻合较好；图12（b）中，为了界定隔振区间，选取绝对位移传递率作为其判定条件，并以dB为单位的绝对位移传递率系数进行表征，现定义绝对位移传递率Td为：配重的绝对位移最大值与振动试验台引起激励的绝对位移最大值之比，则绝对位移传递率系数T′d可表达为

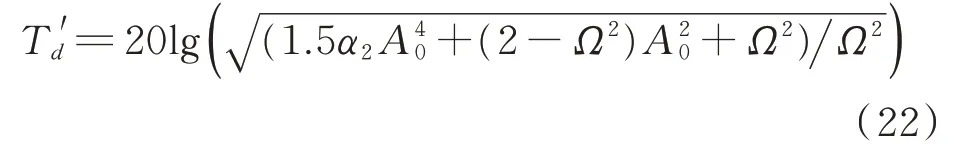
由此可知，在上述参数条件下，碟簧隔振系统在全频域内存在三种振动状态区间，即：当激振频率小于2.8 Hz时，系统处于自锁状态，此时碟簧隔振单元表现为刚性支撑状态，振动被完整的传递；当激振频率介于2.8-14.5 Hz之间时，系统处于共振放大区，此时碟簧隔振系统对基础传递的振动起到放大作用；而当激振频率高于14.5 Hz以后，系统进入隔振区间，此区间内碟簧隔振系统发挥隔振作用，且随着激励频率地进一步增大，系统隔振效果越理想。试验结果与理论计算得到的规律相吻合。