双频激励下含分数阶非线性汽车悬架系统的混沌研究
2022-01-12常宇健孙亚婷陈恩利李韶华邢武策
常宇健,孙亚婷,陈恩利,李韶华,邢武策
(1.石家庄铁道大学电气与电子工程学院,河北石家庄050043;2.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室,河北石家庄050043)
引言
分数阶微积分作为重要的数学分支,于1695年德国科学家Leibniz和法国数学家L′Hopital在探讨1/2阶导数时首次被提出[1]。然而,由于缺乏应用背景支撑等多方面原因,它长期以来并没有得到较多的关注和研究。随着20世纪70年代以来对分形和各种复杂系统的深入研究,分数阶微积分理论及其应用开始受到广泛关注,很多学者对分数阶微积分的基本特性进行研究,在基础理论方面取得了很大进展[2-6]。
进入21世纪以来,分数阶微积分建模方法和理论在复杂黏弹性材料力学本构关系、反常扩散、高能物理等诸多领域有了若干非常成功的应用[7-10],凸显了其独特优势和不可替代性,所以研究含分数阶微积分方程中的典型力学特性和分数阶参数对动力系统的影响很有意义,大量学者进行着这方面的研究[11-13]。
车辆悬架减振装置不仅具有迟滞非线性特性,而且多数阻尼器都具有类黏弹性本构关系,这些黏弹性材料介于弹性和阻尼特性之间,普通的整数阶理论无法准确地描述这种材料的本构关系。为此,很多研究学者开始对黏弹性材料采用分数阶理论进行描述[14-16]。将分数阶理论和非线性理论一起运用到汽车悬架系统中,不仅具有一定的前瞻性,而且由于在悬架系统中加入了分数阶微分理论,可以更准确地描述悬架系统的数学模型。因此本文采用含分数阶微分项的非线性方程来描述汽车悬架系统。
在外界激励的作用下,具有迟滞非线性的汽车悬架系统会产生复杂的非线性动力学行为,如分叉、混沌等。刘剑等[17]建立了两自由度磁流变悬架动力学系统,根据非线性稳定性理论发现了单频谐波激励下系统发生混沌的可能性。黄苗玉等[18]针对两自由度磁流变悬架系统,研究了简谐路面作用下系统随激励频率幅值变化的分叉特性,并利用相平面图、庞加莱截面图等详细描述了通向混沌振动的路径。楼京俊等[19]利用Melnikov方法研究多频激励下的软弹簧Duffing系统的混沌动力学,证明激励频率数目的增加使系统更容易进入混沌状态。毕勤胜等[20]讨论了参外联合激励复合非线性振子的动力学行为,并对其定常解进行了局部分叉分析。杨智勇等[21]建立了双频拟周期动态路面激励函数,并构建了四自由度非线性车辆悬架模型,通过分析系统的庞加莱图、相位图等得到了系统发生混沌时的激励振幅和振动特性。李韶华等[22]研究了具有滞后非线性的汽车悬架在路面拟周期激励作用下发生受迫振动的混沌运动,揭示出此系统中存在从拟周期运动通向混沌运动的可能性。
目前对汽车悬架的研究主要集中在系统的响应分析及悬架的控制技术,对双频激励非线性系统的动力学行为研究,尤其是针对含分数阶的非线性系统在双频激励下的动力学行为研究较少。针对双频激励下的含分数阶非线性汽车悬架系统,本文通过计算Melnikov函数得出了系统的混沌阈值,并分析了参数对混沌区域的影响。
1 双频激励下Smale马蹄变换意义下混沌的解析必要条件
1.1 含分数阶非线性悬架系统建模
汽车悬架非线性模型如图1所示。图中:z0为路面激励位移,z1为系统垂直位移。其运动微分方程为
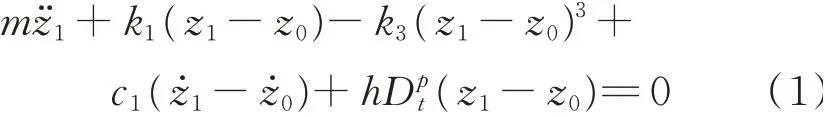
式中m,k1,k3,c1,h和p分别为悬架系统的质量、线性刚度系数、非线性刚度系数、阻尼系数、分数阶项的系数和阶次。
设:相对位移z=z1-z0,则z1=z+z0,式(1)可以转化为
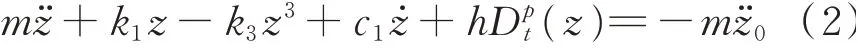
由式(2)可知,含分数阶非线性悬架模型是一种分数阶杜芬系统。拟周期激励表示为:z0=其中,F1,F2为激励幅值;ω1,ω2为激励频率,且ω1,ω2不可有理通约。令,式(2)可以转化为
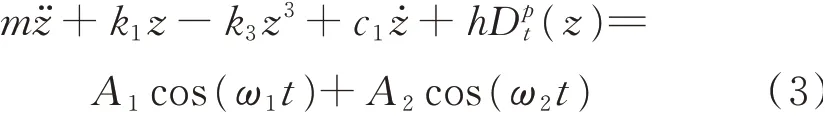
对式(3)进行变量代换,令

则有

1.2 分数阶杜芬系统的异宿轨道
将式(3)写成状态方程的形式

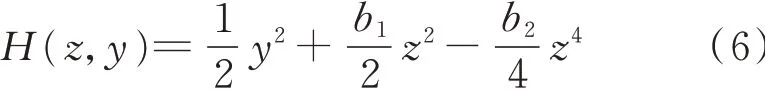
通过M点和N点的异宿轨道满足

对式(7)进行整理可得
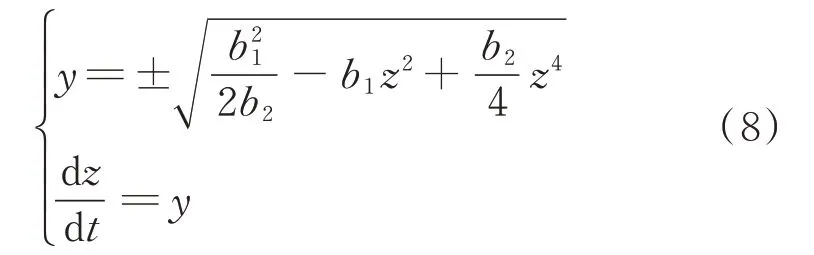
对式(8)进行分离变量与积分分解,从而得到异宿轨道为

1.3 Melnikov函数确定系统混沌边界条件
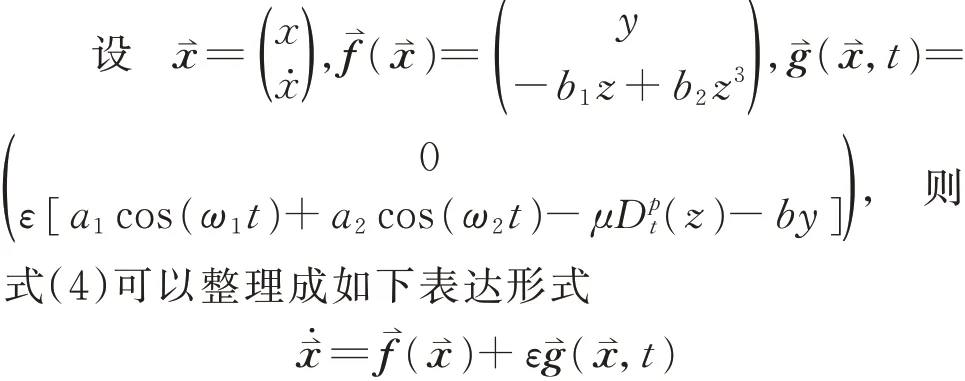
系统的Melnikov函数如下

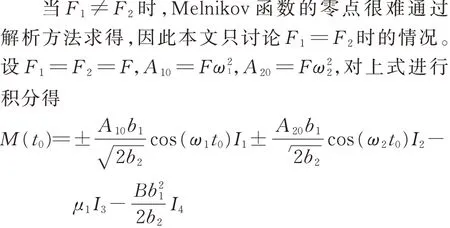
根据Melnikov理论可得发生混沌的边界条件为
其中,


对于式(11)中的I3,由于被积函数中含有分数阶微分项,不能直接进行积分运算,只能通过分数阶微分的定义来进行计算。分数阶导数的定义不像常规整数阶导数有唯一的定义式,根据不同的研究背景,分数阶导数在其发展过程中被给予了多种形式的定义式。目前使用较多的有Riemann-Liouville定义、Caputo定 义 及Grunwald-Letnilov定 义。Riemann-Liouville定义具有良好的数学性质,但在工程中应用受到诸多限制。例如,初值问题在工程中具有重要意义,但常数的分数阶导数在Riemann-Liouville定义下却不为零。Caputo定义在工程应用中,其物理意义更加明确,对于初始条件非零的微分方程,Caputo分数阶微分可以降低其计算难度,但Caputo定义下对分数阶微积分进行离散计算比较困难。Riemann-Liouville形式的分数阶导数方便进行数值运算,但易于离散。本文使用Caputo形式的分数阶导数定义法对分数阶微分方程进行数值计算。Caputo与Riemann-Liouville分数阶微分的定义分别为:

式中Γ(x)为Gamma函数,且Γ(x+1)=xΓ(x)。
通过比较式(12)与(13)分数阶微分的两种定义可知,当x(t)的初值非零时,两者之间的关系为
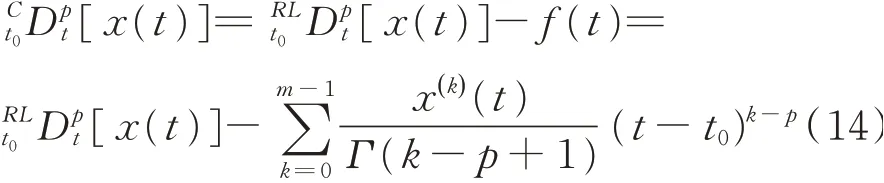
计算高精度Caputo分数阶微分导数的具体过程为:首先,通过改进的直接递推算法[23]来对Riemann-Liouville分数阶微分进行高精度计算;然后,计算出补偿函数f(t);最后,将补偿函数与Riemann-Liouville分数阶微分相结合,得到高精度的Caputo分数阶微分,计算结果可靠。这样可以计算出含有分数阶微分项的积分,得到I3的值。
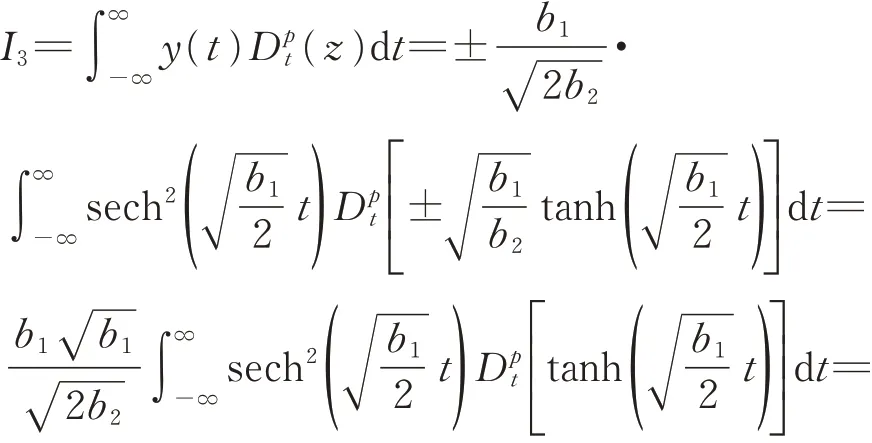

将计算得出的I1,I2,I3,I4带入边界条件式(11)得到系统发生具有Smale马蹄意义下混沌的必要条件表达式为

2 含分数阶非线性悬架系统参数对混沌阈值的影响
根据式(15)所求出的激励幅值F与激励频率ω1,ω2之 间 的 关 系,取m=240 kg,c1=200 N⋅s/m,k1=15000 N/m,k3=30000 N/m3,h=1000,p=0.5,可以确定系统混沌的边界条件,所得混沌边界曲线如图2所示。
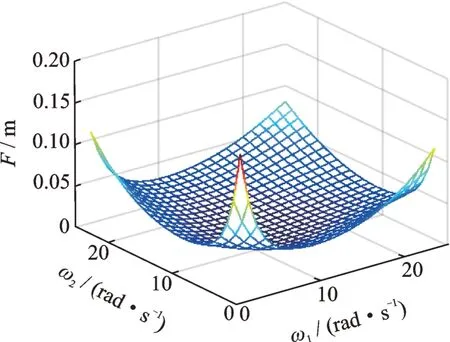
图2 混沌边界曲面Fig.2 Chaotic boundary surface
当F的取值位于混沌边界曲面之上时,则对于充分小的0<ε≤1,系统可能发生Smale马蹄意义下的混沌;若F位于混沌边界曲面下方,系统做稳定的拟周期运动。分别改变c1,k1,k3,h和p的值,可研究系统各参数对混沌边界曲面的影响。其中图3为阻尼系数c1的影响(沿箭头方向c1取值依次增大,分别为160,180,200,220,240);图4为线性刚度系数k1的影响(沿箭头方向k1取值依次增大,分别为11000,13000,15000,17000,19000);图5为非线性刚度系数k3的影响(沿箭头方向k3取值依次增大,分别为26000,28000,30000,32000,34000);图6为分数阶项系数h的影响(沿箭头方向h取值依次增大,分别为600,800,1000,1200,1400);图7为分数阶项阶数的影响(沿箭头方向p取值分别为0.3,0.1,0,0.5,0.7,0.9,1)。

图4 k1对混沌边界曲面的影响Fig.4 Influence of k1 on the chaotic boundary surface

图5 k3对混沌边界曲面的影响Fig.5 Influence of k3 on the chaotic boundary surface

图6 h对混沌边界曲面的影响Fig.6 Influence of h on the chaotic boundary surface

图7 p对混沌边界曲面的影响Fig.7 Influence of p on the chaotic boundary surface
从图中可以看出:
(1)c1越大,混沌阈值越小,发生混沌的可能性越大,阈值随c1变化比较均匀。
(2)k1越大,混沌阈值越小,发生混沌的可能性越大,阈值随k1变化也比较均匀。
(3)k3越大,混沌阈值越小,发生混沌的可能性越大,但非线性项k3的变化对阈值的影响并不十分明显。
(4)h越大,混沌阈值越大,发生混沌的可能性越小,h的改变对阈值变化有明显的影响。
(5)p从0变化到1时,混沌阈值先减小后增大,发生混沌的可能性先增大后减小,且阶数变化对阈值影响较大。
由图可知,悬架系统的各个参数对系统的混沌边界曲线均有影响,其中分数阶微分项的阶数和系数对悬架系统的混沌边界曲线影响很大。由此可知,将分数阶微分项引入汽车悬架系统,比单纯使用整数阶对悬架系统进行描述更能准确描述系统的混沌阈值,这对实际工程中悬架参数的设计和选择具有一定的参考意义和理论价值。
3 数值仿真验证及分析
为了验证边界的正确性,本文随机研究了拟周期频率ω1=7.3 rad/s,ω2=20 rad/s及ω1=8.1 rad/s,ω2=21 rad/s时的情况。首先分数阶项使用幂级数展开法进行数值运算,根据Grunwald-Letnilov形式分数阶导数定义对其进行近似,并将代数方程离散化即可。然后根据系统在双频激励下的时间历程图、频谱图、相图及庞加莱截面图进行判断,最后根据最大Lyapunov指数进一步验证。
3.1 不同激励频率及幅值下的数值仿真运动状态结果研究
进行数值仿真的两组数据在混沌边界曲面的实际位置如图8所示。
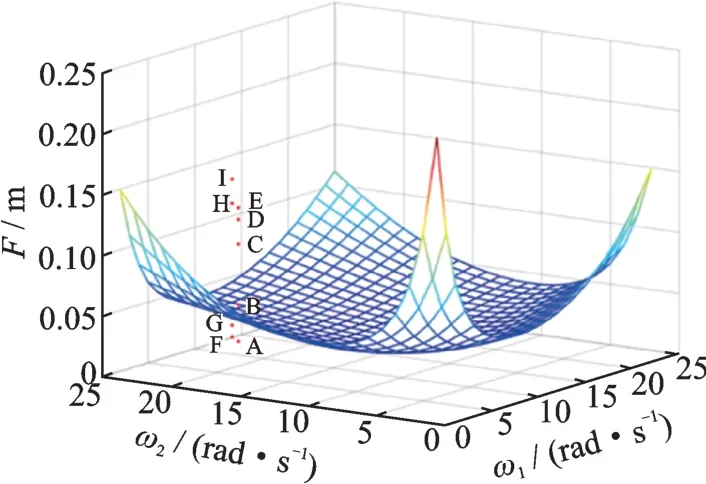
图8 各点在混沌边界曲面的实际位置Fig.8 Position of each point on the chaotic boundary surface
通过数值仿真分析可以得出系统在混沌曲面上下各点的时间历程图、频谱图、相图及庞加莱截面图如图9-17所示。表1为各点取值、位置及运动状态。根据数值仿真结果判断系统的运动形式,进而验证混沌边界曲面的正确性。下面分别对周期运动区域及可能发生混沌的区域选取两组不同激励频率下的点进行比较验证。
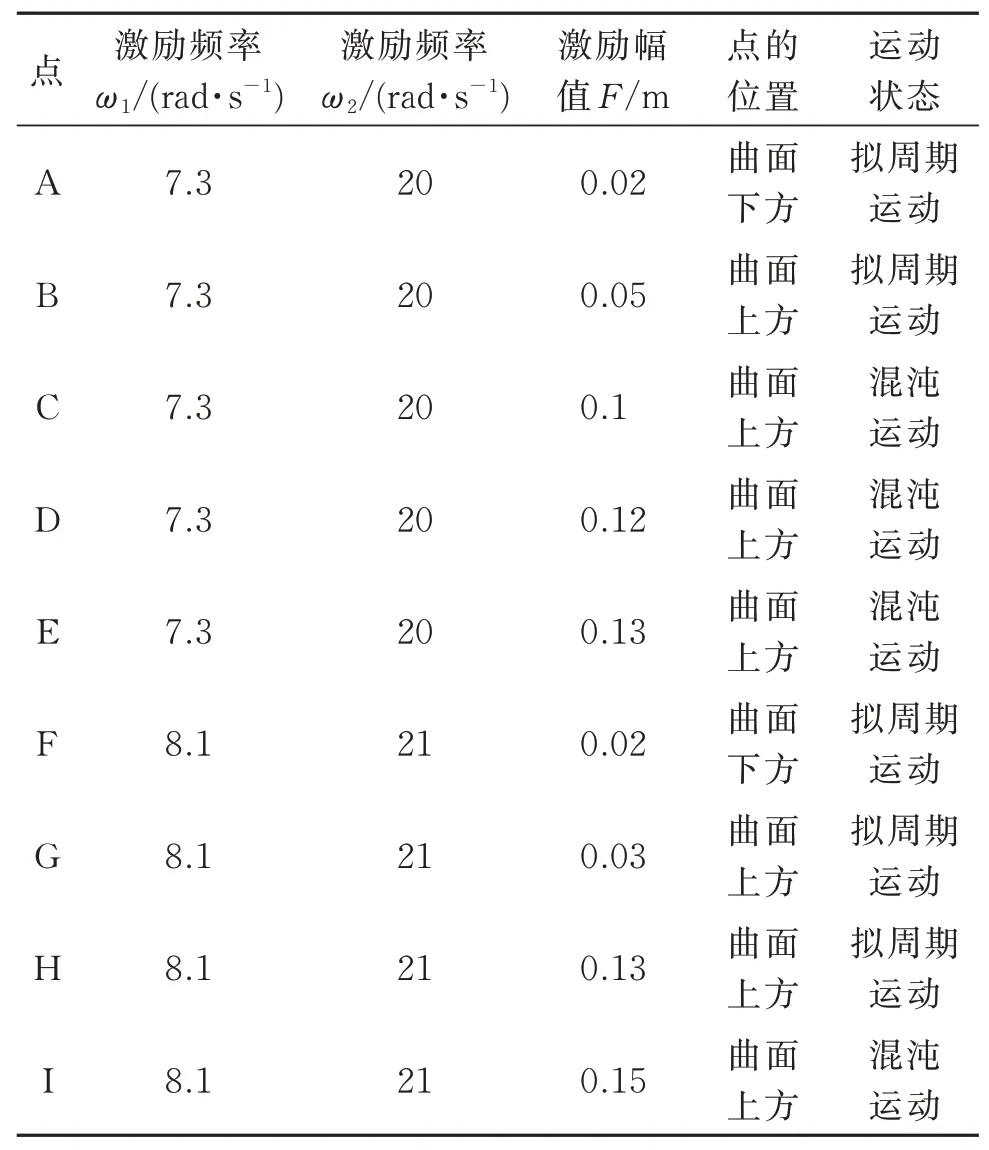
表1 各点位置及运动状态Tab.1 Position and motion state of each point
从图9-13可以得出:图9和10其时间历程图为拟周期运动,频谱图上只有两个与外界激励频率相等的主频率,相图表现为稳定的相轨线,庞加莱截面图类似一个圆环。因此,可以判断系统在此外界激励下做稳定的拟周期运动。A点位于混沌阈值曲面的下方,为拟周期运动。B点虽然位于混沌阈值曲面上方,但解析求得的阈值曲面上方为发生混沌的必要条件,并非充要条件,因此B点仍为拟周期运动。

图9 A点拟周期运动(ω1=7.3 rad/s,ω2=20 rad/s,F=0.02 m)Fig.9 Quasi periodic motion of point A(ω1=7.3 rad/s,ω2=20 rad/s,F=0.02 m)
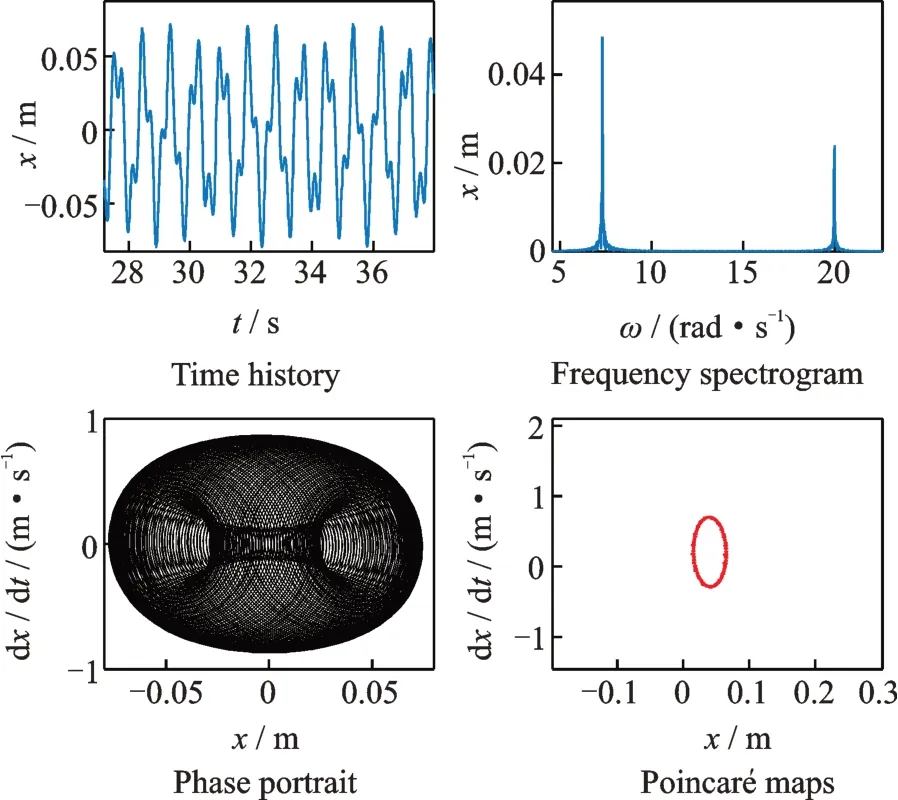
图10 B点 拟 周 期 运 动(ω1=7.3 rad/s,ω2=20 rad/s,F=0.05 m)Fig.10 Quasi periodic motion of point B(ω1=7.3 rad/s,ω2=20 rad/s,F=0.05 m)
C点位于混沌阈值曲面上方,由图11可以看出时间历程图基本没有规律,频谱图上出现多个离散的谱线,相图开始趋于混乱,庞加莱截面图的圆环出现破裂。因此,初步判断系统在此激励下系统开始出现混沌运动,但比较接近于拟周期运动。

图11 C点混沌运动(ω1=7.3 rad/s,ω2=20 rad/s,F=0.1 m)Fig.11 Chaotic motion of point C(ω1=7.3 rad/s,ω2=20 rad/s,F=0.1 m)
随着外界激励幅值逐渐增大,从图12和13可以看出,时间历程图越来越混乱无序,频谱图出现多个离散谱线,且在低频部分表现为连续混乱的频谱,相图轨线越来越混乱,庞加莱截面图圆环完全破裂,呈现为毫无规律的一些离散点,可以判断系统呈现出完全的混沌运动。

图12 D点混沌运动(ω1=7.3 rad/s,ω2=20 rad/s,F=0.12 m)Fig.12 Chaotic motion of point D(ω1=7.3 rad/s,ω2=20 rad/s,F=0.12 m)
从由图14-17可以得出:图14和15的时间历程图为规则的拟周期运动,频谱图只有两条与外界激励频率相等的主频率,相图均表现为稳定的相轨线,庞加莱截面图为一个整齐的圆环。因此,可以判断系统在此外界激励下做稳定的拟周期运动。

图13 E点 混 沌 运 动(ω1=7.3 rad/s,ω2=20 rad/s,F=0.13 m)Fig.13 Chaotic motion of point E(ω1=7.3 rad/s,ω2=20 rad/s,F=0.13 m)
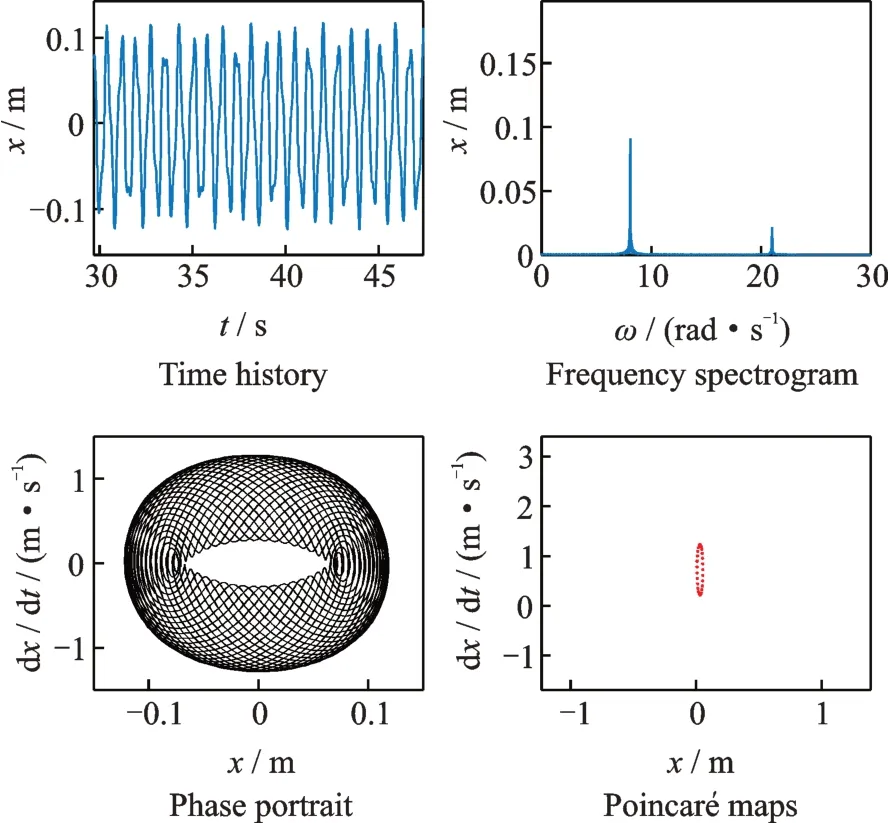
图14 F点 拟 周 期 运 动(ω1=8.1 rad/s,ω2=21 rad/s,F=0.02 m)Fig.14 Quasi periodic motion of point F(ω1=8.1 rad/s,ω2=21 rad/s,F=0.02 m)

图15 G点 拟 周 期 运 动(ω1=8.1 rad/s,ω2=21 rad/s,F=0.03 m)Fig.15 Quasi periodic motion of point G(ω1=8.1 rad/s,ω2=21 rad/s,F=0.03 m)
从图16可以看出,系统的时间历程图表现为较为整齐规则的拟周期运动,频谱图出现多条离散谱,相图开始趋于混乱无序,庞加莱截面图中圆环开始出现破裂。初步判断系统在此外界激励下做拟周期运动,但已经比较接近混沌运动。
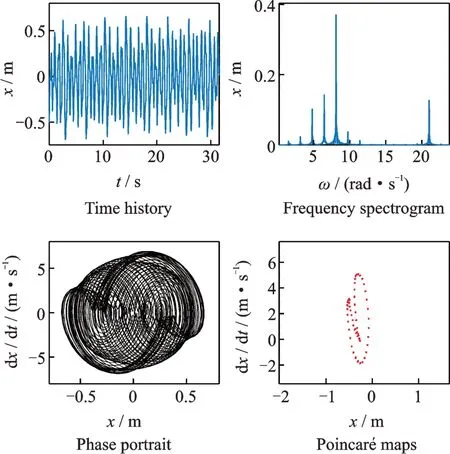
图16 H点 拟 周 期 运 动(ω1=8.1 rad/s,ω2=21 rad/s,F=0.13 m)Fig.16 Quasi periodic motion of point H(ω1=8.1 rad/s,ω2=21 rad/s,F=0.13 m)
从图17可以看出,系统的时间历程图呈混乱无序的混沌运动,频谱图低频段出现连续频谱,相图出现混乱轨线,庞加莱截面图为一些杂乱的离散点。可以判断在此外界激励下,系统做混沌运动。

图17 I点混沌运动(ω1=8.1 rad/s,ω2=21 rad/s,F=0.15 m)Fig.17 Chaotic motion of point I(ω1=8.1 rad/s,ω2=21 rad/s,F=0.15 m)
3.2 最大Lyapunov指数原理及结果
含分数阶非线性系统的振动状态具有非常复杂的动力学特性,可以利用最大Lyapunov指数表征系统在相空间中相邻轨道的发散率,若最大Lyapunov指数为正值,则表示两条相邻轨线随时间变化成指数率增长,系统运动具有混沌状态;若最大Lyapunov指数为负,则表示系统对初值不敏感,系统状态收敛到平衡点,此时系统具有拟周期运动特性。为验证上述混沌边界曲面的正确性,使用MATLAB软件对含分数阶非线性汽车悬架系统进行数值仿真分析。
进行数值仿真分析时,对最大Lyapunov指数使用Wolf重构算法,仿真程序中选取的初始条件为初始位移为-0.5 m,初始速度为0.5858 m/s,分数阶项初始值为0.1,步长为计算A-I各点最大Lyapunov指数及运动状态如表2所示。所有出现混沌的点都位于边界曲面上方,据此可以进一步判断其运动状态的正确性。根据时间历程图、频谱图、相图及庞加莱截面图判断所得各点运动状态与根据最大Lyapunov指数判断结果一致,因此可以验证所得混沌边界曲面正确。
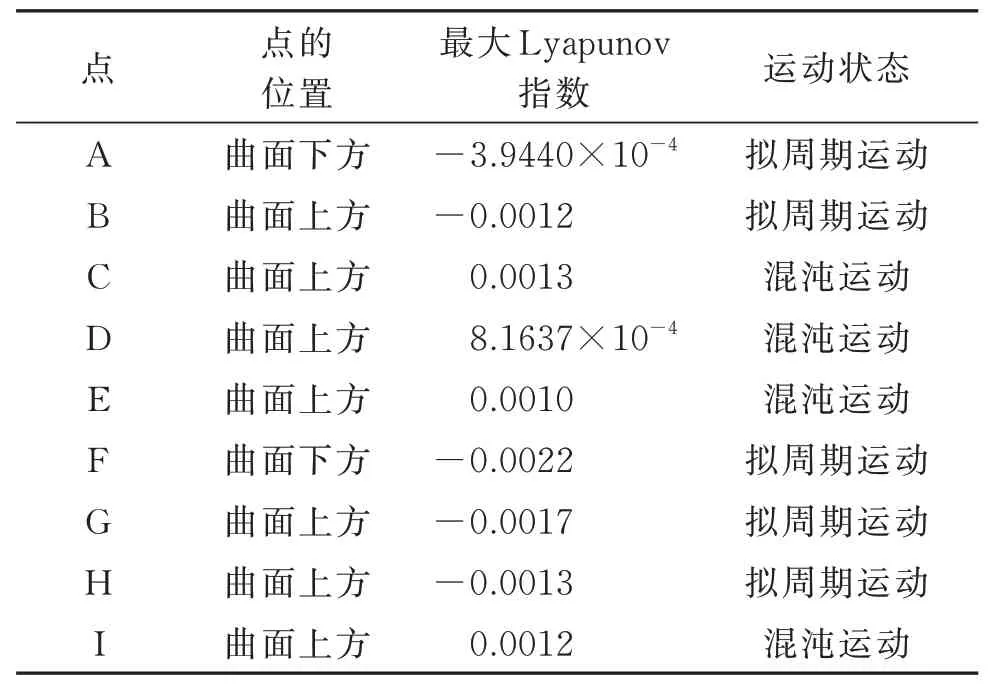
表2 各点最大Lyapunov指数及运动状态Tab.2 Maximum Lyapunov exponent and motion state of each point
4 结论
本文针对含分数阶非线性特性的1/4汽车悬架系统,研究双频激励下系统的动力学响应。
(1)通过构建含分数阶1/4汽车非线性悬架系统,应用Melnikov解析方法得到系统发生混沌的解析必要条件。
(2)采用数值仿真得到汽车系统响应特征,并结合最大Lyapunov指数分析,验证了含分数阶非线性悬架系统在一定条件下存在混沌运动,且随着激励幅值的增加,悬架系统运动状态为拟周期运动到混沌运动。通过系统最大Lyapunov指数和系统响应验证了混沌阈值曲面的正确性。
(3)分析表明系统的刚度、阻尼及分数阶项系数和阶次均对混沌边界曲面有一定影响,且分数阶项参数对系统的影响较大,分析结果可以为悬架系统参数的选择及混沌行为的研究提供借鉴意义。
