经验小波变换-同步提取及其在滚动轴承故障诊断中的应用

李志农，刘跃凡，胡志峰，温 聪，王成军

（1.南昌航空大学无损检测技术教育部重点实验室，江西南昌330063；2.安徽理工大学矿山智能装备与技术安徽省重点实验室，安徽淮南232001）

引言

轴承是机械设备中起承载作用的关键零部件，对轴承进行及时准确的故障诊断在机械设备的安全使用过程中至关重要［1］，目前针对轴承的故障诊断取得了一定的进展，文献［2-3］是基于滚动轴承的微弱特征提取研究；潘海洋等［4］提出了基于拉普拉斯特征映射流形学习算法和改进多变量预测模型，实现了滚动轴承的特征提取和故障识别全过程；文献［5-9］是针对变工况下的滚动轴承故障诊断方法的研究；文献［10-13］开发了针对滚动轴承的故障诊断系统；文献［14-16］针对不同滚动轴承的故障类型进行了故障智能识别研究。然而，在复杂工况下，从轴承的故障信号中提取准确的故障频率及时变特征仍是一个一直在探讨的问题。文献［17］采用了经验小波变换（EWT）对轴承故障信号进行分解，对提取得到的模态进行Hilbert变换，得到Hilbert谱，该方法能够表征故障信号的时频特性，但是Hilbert变换会将两信号的频率差作为所求解的信号的频率特征，因此得到的瞬时频率和瞬时幅值会与实际信号有所偏差。文献［18］采用谱峭度和同步提取变换方法应用到变转速的轴承故障诊断中，为变转速轴承故障诊断提供了新思路，但是当信号的瞬时频率差过小时，传统的同步提取变换方法［19］处理故障信号时易发生混叠，为解决上述问题，本文提出了一种基于同步提取变换（SET）和经验小波变换（EWT）［20］的滚动轴承故障诊断方法，为了叙述方便，将该方法称为EWT-SET方法，该方法结合了SET和EWT优点，即高时频聚集性与信号的有效分解。进行了仿真和实验验证，同时与传统的SET诊断方法进行了对比研究，仿真结果验证了提出的EWT-SET的时频结果相比传统的SET有更清晰的瞬时频率轨迹与更高的频率分辨率，实验验证表明，该方法能够有效地提取故障轴承的故障频率，同时也能清晰地表示故障信号的时变特性，可以有效用于分析滚动轴承的损伤程度。

1 经验小波变换-同步提取变换故障诊断方法

1.1 同步提取变换

同 步 提 取 变 换（SET）［19］是 短 时 傅 里 叶 变 换（STFT）的后处理过程，因此SET的理论推导先从STFT开始，STFT定义式如下

式中s(u)为待分析的信号，g(u)为可移动的窗函数。将一维的时间信号变换到了二维的时间和频率域中，令gω(u)=g(u-t)⋅ejωu，根 据帕斯瓦尔定理对式（1）进行变换，得到

式中S(ξ)与分别为s(u)与gω(u)的傅里叶变换，上标*表示取复共轭，Gh(ω-ξ)为窗函数的傅里叶变换。为了表达方便，对STFT的时频结果G(t，ω)添加相移ejωt，由于观察到的时频谱均为幅值谱，因此增加相移不会影响结果，令

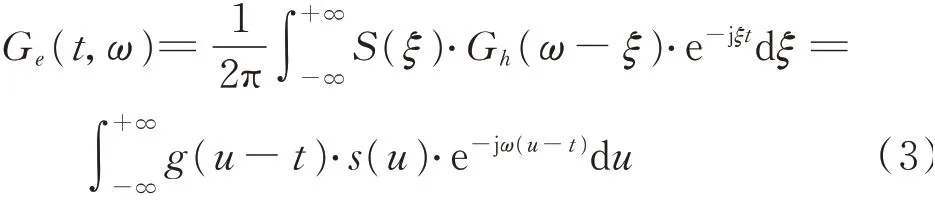
取 一 个 单 分 量 信 号sh(t)=A⋅e-jω0t，它 的 傅 里叶变换为Sh(ξ)=2πA⋅δ(ω-ω0)，A表示振幅，ω0表示频率，将信号sh(t)的傅里叶变换代入式（3）得到单分量信号的STFT表达

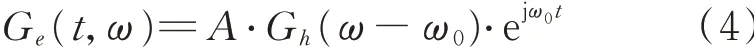
计算式（4）中Ge(t，ω)对时间的导数能够得到STFT的瞬时频率轨迹ω0(t，ω)为

若Ge(t，ω)不为零，式（5）对任何的(t，ω)都成立，STFT的瞬时频率的系数应该总是等于ω0，并且瞬时频率轨迹ω0(t，ω)在时频域中的表示为，在任意时间t下，频率范围[ω0-Δ，ω0+Δ]内的数值恒为ω0（Δ表示窗函数的频宽），因此STFT受窗函数频宽的限制难以精确表示瞬时频率轨迹。式（4）中，根据海森堡测不准原理，为得到最佳的时间与频率分辨率，选取窗函数为高斯窗，因此Gh(ω)是紧凑的，由于|ejω0t|=1，所以|Ge(t，ω)|在ω=ω0时取得最大值，并且能量最高，SET的目的便是提取ω0(t，ω)中ω=ω0时的瞬时频率轨迹，以及时频系数|Ge(t，ω0)|，从而使STFT的时频表达逼近理想时频分析。设SET的时频表达为Te(t，ω)，定义如下表明，Te(t，ω)只保留STFT瞬时频率轨迹ω0(t，ω)范围内，即[ω0-Δ，ω0+Δ]范围内中ω=ω0时的时频系数，其余的时频系数被移除，因此相比STFT会有更高的能量聚集度和频率分辨率。称δ(ωω0(t，ω))为同步提取算子（Synchroextracting Operator，SEO）。为了更准确地表示SEO，求Ge(t，ω)对t的导数

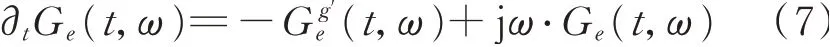
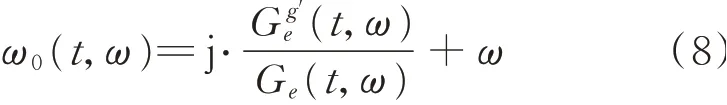
将sh(t)写为调幅-调频（AM-FM）形式，sh(t)=A(t)⋅ejφ(t)，φ(t)表示相位，φ′(t)为频率，由式（6）和（9）可以得到sh(t)的SET表达式

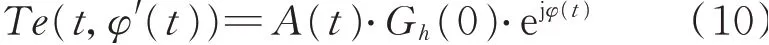
因此，信号sh(t)可由下式重构

以上是SET处理单分量信号的过程，若对于多分 量 信 号表 示 各 分 量信号的相位，φ′k(t)表示频率，SET的频率分辨率由于受到窗函数频宽Δ的限制，任意两个分量必须满足即 不同分量的瞬时频率必须有一定的间隔SET才能有较好的结果，否则就会产生频率混叠，时频图上看不到完整的瞬时频率信息，而故障信号通常都是复杂的非平稳信号，如果直接对故障信号进行SET，时频图上关键的故障信息很有可能会被其他相邻较近的频率成分所覆盖，从而造成误判以及不可预知的后果，因此，本文提出结合EWT对SET进行改进。

1.2 经验小波变换

在经验小波变换（EWT）中，首先要对信号频谱进行自适应的分割，将傅里叶谱[0，π]分割成N个连续的部分，设ωn表示相邻两个部分的边界，定义ω0=0，ωN=π，其余N-1个边界可以选择为傅里叶谱相邻局部各极大值的中点。每个部分表示为以 每 个ωn为 中心，定义带宽Tn=2τn的滤波器过渡带，经验尺度函数和经验小波函数定义如下：

式（12）和（13）实际上提供了低通滤波器和一系列带通滤波器，对原信号进行滤波后能得到各个信号分量。设待分解信号为f(t)，可以用类似经典的小波变换方式来定义经验小波变换，细节系数可由信号与经验小波函数的卷积得到，逼近系数可由信号与尺度函数的卷积得到

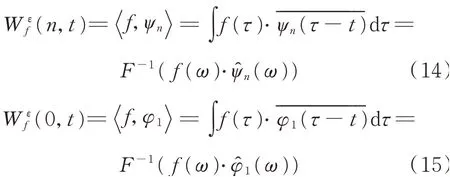
F-1(⋅)表示傅里叶反变换分别由式（12）和（13）定义，分别是φ1(t)和ψn(t)的Fourier变换，信号f(t)的重建如下

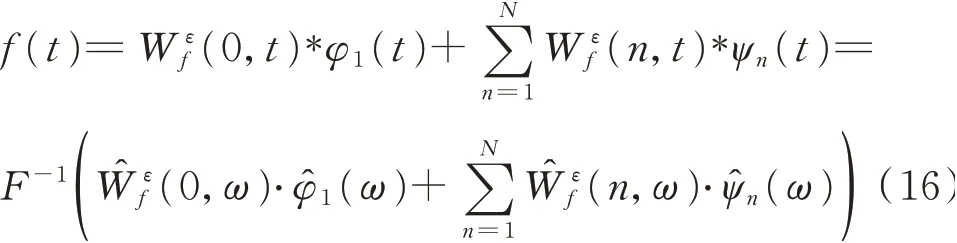
f(t)各经验模态fk(t)定义如下

EWT的关键在于对频谱的自适应划分，对频谱分割的合理性直接影响到对信号分解的效果，在频谱分割前需要确定频谱极大值的数量N，如果已知信号的频谱特点，可预先给定合适的N进行EWT，对于未知信号，Gilles在文献［20］中提到了一种能够自动确定N的算法，设表示在频谱上检测到极大值的集合，数量为M，将这M个极大值降序排列后满足M1＞M2＞…＞MM，定义阈值MM+α(M1-MM)，α∈(0，1)，只保留大于该阈值的极大值点，通过调整参数α能够得到合适的N。若N取值过小，则不能对原始信号进行有效分解，N取得过大则会错误地分割某些变频信号的频谱，因此N需要慎重选择。为此，本文采用通过预先观察待分析信号的频谱的方法来确定合适的N，随后将检测到的极大值降序排列取前N个，在实际应用中，若噪声的频谱幅值小于信号各频率分量的幅值，所确定的N个极大值几乎不会受到噪声的影响。即使检测到了因为噪声而产生的极大值，也可以只取前N个极大值来避免由噪声产生的较小的极大值。

目前深基坑开挖研究对围护桩位移变化规律研究较多[6-9]，但对内支撑轴力分析较少，且没有明确的规律.所以本文就工程实例来主要研究深基坑内支撑轴力变化进行研究，为类似工程提供参考.

1.3 EWT-SET故障诊断方法

SET提取了STFT在信号瞬时频率轨迹处的时频参数，去除STFT多数发散的能量，因此SET的时频结果具有能量集中，时频分辨率高的特点，EWT能够自适应地将复杂信号有效分解成若干个带宽有限的信号分量，能较好地提取信号的时变特性，本文所提方法结合了SET和EWT在时频分析方面的优点，提出的SET-EWT故障诊断方法具体步骤如下：

（1）利用EWT对轴承故障信号进行分解，得到N个模态分量。

（2）对每个模态分量用SET进行时频分析，得到各个模态高能量集中的时频分布与时变特征。

（3）将每一个模态的时频结果叠加，得到故障信号的EWT-SET的时频分布。

2 仿真研究

2.1 含相邻的频率成分的处理能力对比研究

这里，设计了两个分量信号f1(t)=sin(2πf1t)与f2(t)=sin(2πf2t)，设f(t)为上述两个不同频率正弦波简单叠加构成的，如下式所示

图1 EWT-SET和传统SET时频图Fig.1 Time-frequency diagram of EWT-SET and traditional SET

2.2 调幅调频信号处理能力的对比研究

仿真信号f2（t）由正弦信号x1(t)和两个调幅调频信号x2(t)，x3(t)构成，表达式如下

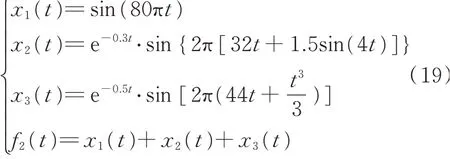
仿真信号f2（t）的时域波形与频谱如图2所示。利用EWT-SET和SET分别对f2（t）进行时频分析，得到的时频分布如图3（a）和（b）所示。在上述仿真信号的基础加入噪声，构建信噪比为13 dB的仿真信 号，EWT-SET和SET的 结 果 如 图3（c）和（d）所示。

图2 仿真信号f2（t）的时域和频域波形Fig.2 The time-domain and frequency-domain waveform of simulated signal

由图3（a）可知，EWT-SET能够清晰地表示信号的瞬时频率轨迹，EWT通过自动检测信号频谱局部极大值后自适应分割频谱，随后再对EWT分解出的模态分量进行SET。提出的EWT-SET方法在处理该信号的时候避免了因Δφ′(t)过小而得不到较好的结果。由图3（b）可知，传统的SET方法在0至2 s内频率混叠现象最严重，随着分量x3(t)的瞬时频率逐渐增加，分量x1(t)的频率差增大，混叠现象就不再发生，分量x2(t)周期性与x1(t)产生频 率 混 叠，对 比 图3（c）和（d），在 加 入 噪 声 后，EWT-SET仍能够较好地分割频谱，并较为清晰地表示出信号的瞬时频率轨迹。而在图3（d）中，SET的时频结果依旧存在混叠情况。

图3 EWT-SET和SET得到的时频分布Fig.3 The time-frequency diagram of EWT-SET and SET

对于多分量的变频信号，在每个分量的频带没有重叠部分时，频谱中可以确定分量的个数，假设每个分量的频谱都存在一个幅值最大的频率点，也是整个信号能够检测到的频率极大值点，由于不同分量的频带没有重叠，则通过选取频率极大值点之间的频谱幅值最小处所对应的频率点作为频谱分割点，以便能够有效地将各分量分离开。

3 实验研究

为了进一步验证EWT-SET算法的有效性，将提出的EWT-SET方法应用到滚动轴承的故障诊断中，并与传统的SET进行对比。轴承数据来源为凯斯西储大学，轴承类型为深沟球轴承，规格如表1所示。轴承振动信号由加速度传感器采集，试验台如图4所示。采样频率12 kHz，转速为1797 r/min，在轴承外圈分别用电火花加工直径为0.1778与0.5334 mm的缺陷，用来模拟轴承的轻微与严重损伤。由于轴承发生故障时所测得的信号是调制信号，高频率的共振频率通常作为载波，调制波通常为低频的冲击信号，故障信息往往都包含在低频的冲击信号中，很大程度上会影响故障诊断，因此，需要对故障信号进行Hilbert变换解调，原信号的时域波形与解调后的频谱如图5和6所示。

图5 轴承外圈故障信号时域波形Fig.5 Time-domain diagram of fault signal of bearing outer ring

表1 轴承规格Tab.1 Bearing specifications

图4 实验装置结构图Fig.4 Experimental device structure diagram

经过计算，轴承外圈故障频率应为107 Hz，由图6（a）和（b）中均能看出故障频率基频，图6（a）中的频率成分较为明显，而图6（b）中出现了很多的频率分量，仅从频谱上难以看到故障频率的倍频，同时，图6（a）和（b）中的频谱也无法表示轴承外圈故障信号的时变特性。

根据频谱分析，N的取值分别为13和9，如图6所示。分别采用EWT-SET与传统SET对不同损伤程度的外圈故障信号做时频分析，得到的时频分布 如 图7所 示。其 中 图7（a）和（c）为 利 用EWT-SET方法对两种不同损伤程度进行时频分析得到的结果，图7（b）和（d）为利用传统SET方法对两种不同损伤程度进行处理得到的时频分布。为了证明所提方法的优越性，这里，给0.1778 mm损伤的轴承信号加入信噪比为10 dB的白噪声，分别采用EWT-SET与传统SET进行分析，得到的时频分布如图7（e）和（f）所示。

轴承轻微损伤时，由图7（a）可知，利用EWT-SET方法得到的时频分布能够看到一系列清晰的故障特征频率和相应的倍频，且1X至9X持续存在，更高阶的倍频分量比较微弱，且呈周期性的激发。而在图7（b）中，传统的SET方法虽然也能够看到故障频率及倍频，但是相比EWT-SET的结果，关键的故障频率倍频轨迹不够清晰，并且在相邻倍频之间出现了额外的瞬时频率轨迹，这个现象出现的原因正是仿真实验中图1所表现的Δφ′(t)过小，而EWT-SET预先经过图6的频谱分割，再进行SET，得以清晰地表现故障频率及其各个倍频的时变特性，有效地诊断出故障。

图6 故障信号解调后频域波形（虚线表示EWT对频谱分割的边界）Fig.6 Frequency domain waveform after fault signal demodulation（The dotted line indicates the boundary of the EWT segmentation of the spectrum）

轴承出现严重故障时，由图7（c）能够看出，故障基频与2X至9X均呈现周期性的激发，随着倍频阶数增加，振幅逐渐微弱，而图7（d）中SET的结果较为普遍的存在频率混叠现象，虽然也能够看出故障频率的周期性激发，但是各倍频的频率轨迹十分模糊，尤其在400-800 Hz处，给故障诊断带来困难。

图7 轴承外圈故障的时频分布Fig.7 Time-frequency distribution of bearing outer ring signal

对轴承故障信号加入噪声时，EWT-SET的时频结果中仍能观察到清晰的故障频率倍频，隐约能观察到高阶倍频分量的冲击特性，SET的时频结果频率混叠情况加重，信号高阶倍频处的时频结果几乎被噪声成分完全覆盖。

通过上述分析，EWT-SET能够准确地表示轴承故障的时频特性，得到的时频结果清晰地反映了轴承外圈故障的关键信息。轻微损伤时，故障基频和较低阶的倍频都持续稳定存在，高阶倍频均呈现冲击特性，而严重损伤时较低阶的故障频率倍频甚至故障基频也会出现冲击特性，能够作为轴承损伤严重程度判断的依据，由此可见，EWT-SET方法为轴承故障诊断提供了一种有效的诊断方法。

4 结论

提出了一种基于同步提取变换（SET）与经验小波变换（EWT）的轴承故障诊断方法，即EWT-SET方法。该方法首先通过EWT对故障信号的频谱进行自适应分割，构造正交小波滤波器提取故障信号频谱的主要频率分量，在经过小波逆变换得到各经验模态，随后对每个模态进行同步提取变换，以时频谱的形式表示各模态的瞬时频率轨迹和瞬时幅值，最后将所有模态的时频谱叠加得到故障信号的时频分布，提出的方法预先通过EWT对信号进行模态分解，再对每个模态进行SET，在很大程度上解决了信号瞬时频率分量距离过小导致SET的结果出现瞬时频率混叠的问题。最后，将所提方法成功应用到了滚动轴承故障诊断中，实验结果表明，相比传统SET方法，EWT-SET具有明显的优势，利用EWT-SET方法能揭示轴承不同损伤程度时的振动特性，可以作为轴承损伤程度判断的依据。