小波滤波与最大相关峭度解卷积参数同步优化的轴承故障诊断

张 龙，蔡秉桓，熊国良，刘志刚，邹 孟，吴荣真，甄灿壮

（1.华东交通大学机电与车辆工程学院，江西南昌330013；2.中国铁路南昌局集团有限公司南昌车辆段，江西南昌330201）

引言

滚动轴承作为旋转机械最主要的零部件之一被广泛应用于机械、交通、航空航天等重要领域，同时由于工作坏境恶劣也是最易发生故障的部件。滚动轴承一旦发生故障且未及时发现，则可能引起不可估量的后果。因此如何准确判断滚动轴承健康状态对于提高机械设备的可靠性、可用性和保障设备安全运行至关重要［1-2］。然而振动信号常常会淹没在强背景噪声以及高幅值偶然性干扰冲击中，导致故障特征信息难以提取。因此准确判断滚动轴承故障的关键是在复合干扰因素下从振动信号中提取出周期性的故障冲击成分，因此有效的信号处理方法很重要［3］。

当轴承局部缺陷撞击滚动轴承其他表面时将会产生一系列的脉冲，这些脉冲将会激起轴承以及机械系统的共振。连续冲击引起的脉冲响应将会对原始信号进行幅值调制，目前滚动轴承故障诊断中，调制影响、干扰冲击以及背景噪声是主要的阻碍。共振解调是提取滚动轴承故障冲击特征的主要方法［4-7］，其通过带通滤波器在共振频率附近进行带通滤波以尽可能消除噪声等干扰成分，进而对滤波后信号进行包络解调得到轴承的故障特征频率。梁霖等［8］利用格形搜索算法以峭度最大为准则选择复平移Morlet小波的中心频率和带宽参数。考虑这种搜索方式比较耗时，Antoni［9］提出快速谱峭度方法二进分布的有限脉冲响应FIR滤波器对整个信号的频带进行划分并以滤波信号时域峭度最大的频带作为最优带通滤波频带。Zhang等［10］采用遗传算法优化带通滤波器，并以峭度最大作为优化指标选择最优滤波器对原始信号进行滤波处理。由于Morlet小波与轴承的故障冲击响应更为相似，因此近年来Morlet小波滤波器被广泛应用于提取淹没在噪声中的故障特征［11-14］。

虽然上述各种共振解调方法取得了较好的滤波效果，但是仍存在带内噪声无法消除的问题，尤其是在强噪声的情况下，导致诊断效果不佳。为此，一系列增加带内去噪的复合诊断方法相继被提出。Su［15］利 用 山 农 熵 为 指 标 优 化Morlet小 波 滤 波 器 对原始信号进行带通滤波处理，然后采用自相关增强进行带内噪声二次消除。然而当信号中存在强噪声干扰时，山农熵难以有效衡量周期性发生的故障脉冲。Jiang［16］以改进的山农熵为优化指标对Morlet小波参数进行优化，对滤波后信号进一步采用SVD分解完成带内噪声二次消除。然而其前后处理是基于不同优化指标分别进行优化，难以达到最优效果。He等［17］以最优Morlet小波滤波器与稀疏编码收缩分别进行带通滤波和带内噪声消除。上述文献对带内噪声做了进一步处理，改善了特征提取效果，但如下问题值得进一步研究。首先，上述方法的前后两个处理步骤所采用的优化指标没有考虑轴承瞬态故障冲击的周期性发生特点，从而易受偶然性干扰冲击的影响；其次，前后处理步骤采用各自独立优化，难以保证诊断的总体效果。

基于上述分析，本文提出一种Morlet小波滤波与最大相关峭度解卷积（Maximum Correlated Kurtosis Deconvolution，MCKD）参数同步优化的轴承故障诊断方法。鉴于遗传算法等传统启发式优化算法存在易陷入局部最优解等缺点，本文考虑到小生境遗传算法（Niching Genetic Algorithms，NGAs）可以更好地保持解的多样性，同时具有很高的全局寻优能力和收敛速度，将NGAs对Morlet小波滤波器中心频率f0和带宽β、MCKD滤波器长度L和周期T进行同步联合优化，以考虑轴承故障冲击特征周期特点的相关峭度（Correlated Kurtosis，CK）为优化指标，实现前后两个步骤参数的自适应同步优化。基于最优参数组合，利用Morlet小波进行共振带通滤波消除偶然性冲击等强噪声干扰，MCKD进行带内残留噪声、传递路径的二次消除，最后通过包络谱进行轴承故障识别，完成故障诊断。

1 理论背景及提出的方法

1.1 Morlet小波滤波解调

对于一个能量有限信号x(t)，其连续小波变换（Continuous Wavelet Transform，CWT）可表示为x(t)与小波函数的内积［18］。表达式如下

式中a为尺度参数，τ为时移参数，φ*(t)表示小波函数φ(t)的共轭函数。

Morlet小波的指数衰减震荡形式与轴承故障冲击波形十分接近，因此被广泛用于故障冲击特征提取［19-20］。Morlet小波实质上是一个高斯函数与正弦信号的乘积，其数学表达式为

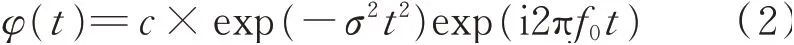
图1 Morlet小波时域及频域波形Fig.1 Time domain and frequency domain of Morlet wavelet

从频域上看，Morlet小波可以看作一滤波窗口，由于其为高斯窗口，故将Morlet的半功率带宽定义为

将β代入式（3）得到以[f0-β/2，f0+β/2]为通带的带通滤波器，即

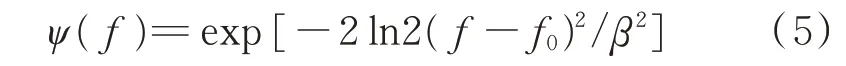
根据卷积定理，小波滤波的过程可以采用频域相乘的方式进行

式中WT(f0，β)为滤波后信号。为了使滤波器更好地选择振动信号中的冲击特征成分，需对参数f0，β进行相关优化。

1.2 最大相关峭度解卷积（MCKD）

最小熵解卷（Minimum Entropy Deconvolution，MED）作为早期解卷积技术以峭度最大为指标被广泛应用于轴承故障诊断，然而峭度指标难以考虑轴承故障的周期性发生特性，易发生误诊。MCKD是由McDonald等在MED的基础上提出的一种以相关 峭 度（CK）为 评 价 指 标 的 解 卷 积 技 术［21-22］。MCKD算法的本质是寻找一个滤波器使得滤波后信号的CK最大。带有局部故障的滚动轴承运行时会产生周期性冲击信号y，但是由于信号受传递路径以及环境因素的影响，传感器采集到的信号为

式中h代表传输路径影响；e为环境噪声。

从实际采集的信号x中恢复出周期性冲击信号y，消除路径和噪声影响、突出周期性故障特征，这一过程被称为解卷积。即

式中L表示FIR滤波器的长度。

经过M次移动后的相关峭度可以表示为

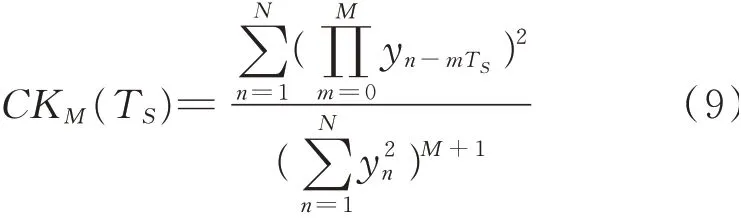
式中TS表示迭代周期对应的采样点数。N表示输入信号的样本数。

MCKD的故障特征增强的迭代过程如下：

步骤1：输入由加速度传感器测得的振动信号x，以及确定故障周期T；

步骤2：根据输入信号x计算X0XT0和(X0XT0)-1；

步骤3：设置初始滤波器系数f=［0 0…1-1…0 0］T；

步骤4：计算滤波后的输出信号y；

步骤6：计算新的滤波器系数f；

步骤7：根据下式计算迭代误差

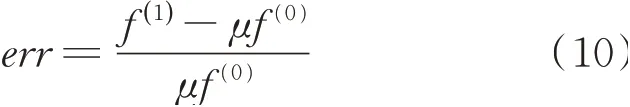
如果计算出的err比给出的迭代误差小则计算终止；否则返回步骤3继续计算［23］。

1.3 小生境遗传算法

遗传算法（Genetic Algorithms，GA）在故障诊断领域已经得到了广泛应用［24］。通过模拟物种“适者生存”的自然行为而被广泛应用于寻找最优解，也常用于各种线性和非线性问题上。然而其存在易陷入局部最优解、收敛速度慢等缺陷，难以保证在全局范围内进行寻优，导致优化结果难以达到最优。

生物学上，小生境（niche）是指在特定环境中一种组织（organism）的功能，把有共同特性的组织称作物种（species）。小生境技术就是将每一代个体划分为若干类，每个类中选出若干适应度较大的个体作为一个类的优秀代表组成一个群，在种群中以及不同种群中之间杂交、变异产生新一代个体群。算法通过修改个体的适应度实现种群的多样性，以防止算法早熟并提高搜索的效率。基于这种小生境的遗传算法（Niching Genetic Algorithms，NGAs），可以更好地保持解的多样性，同时具有很高的全局寻优能力和收敛速度，特别适合于复杂多峰函数的优化问题。

NGA的主要实现过程可以分为以下几个步骤：

步骤1：随机生成D个初始染色体组成初始群体P(t)，并求出各个个体的适应度。

步骤2：依据各个个体的适应度对其进行降序排序，保存前K个染色体（K＜D）。

针对村镇银行起点低、专业人员素质跟不上的现状，有针对性地在员工中招聘一批会计学、审计学专业毕业生，并进行多岗位轮岗培训、跟班学习，尽快培养内部审计专业人才。从社会人士中招聘一定数量的取得国家认定的会计师、审计师、注册会计师资格，并具有丰富财务会计和审计工作经验的人员，有针对性地物色内部审计人才。强化人才培训教育，有针对性地组织内部制度文件培训和同有关知名院校对接培训，出台政策鼓励现有岗位员工参加国家会计师、审计师和注册会计师等专业资格培训和考试，迅速培养一批专业技术人才。■

步骤3：进行选择、交叉、变异运算，得到P1(t)。

步骤4：小生境淘汰运算。将第3步得到的D个染色体和第2步保存的K个染色体合并，新群体拥有D+K个染色体；按照下式计算新群体中每两个染色体之间的海明距离，重新计算每个染色体的新适应度值。

步骤5：依据新适应度值对各个个体进行降序排序，记忆前K个染色体。

步骤6：终止条件判断。若不满足终止条件，则更新进化代数计数器t=t+1，并将第5步排序中的前D个染色体作为新的下一代群体P（t），然后转到第3步；若满足终止条件，则输出计算结果，算法结束。

1.4 提出的轴承故障诊断算法

Morlet小波滤波器的两个重要参数——中心频率f0与带宽参数β决定了特征提取效果好坏。β若太小，则不能有效包含轴承故障特征信息，若太大，则会引入更多的噪声干扰成分。β的值通常设置为不小于3倍最大故障特征频率［25-26］，而对于外圈固定的滚动轴承而言，最大故障特征频率为内圈故障特征频率BPFI。本文设置带宽β搜索范围如下

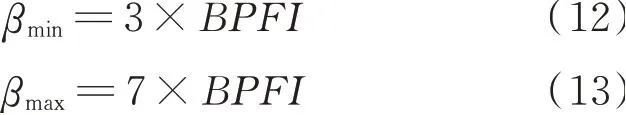
中心频率f0的取值范围需要满足采样定理及小波允许条件，设置如下

式中fr表示转频，fs表示采样频率。

MCKD已被证明是一种有效的解卷积方法，然而其输入参数周期T和滤波器长度L需要人工预先设置，否则不能保证最优解卷效果。由于故障确诊之前，轴承故障类型是未知的，因此本文根据内、外圈以及滚动体故障特征频率取并集设置MCKD的参数周期T的寻优范围。另外，对于滤波器长度L的选择，若滤波器长度过长，虽然解卷积效果可能会有所增强，但其在计算时所消耗的时间同时也将增大，影响计算效率。通常，滤波器长度将设置在300-1000左右，本文在尽可能地涵盖其所能选择的候选值的同时，为了避免计算效率过低，统一设置L的寻优范围为［2，1500］。本文提出方法的具体流程如图2所示，实现过程如下：

图2 本文所提方法流程图Fig.2 Flow chart of proposed method

1）采集原始振动信号并输入；

2）设置小生境遗传算法初始条件如表1所示；

表1 NGA初始参数Tab.1 Initial parameters of NGA

3）Morlet小波滤波器的中心频率f0和带宽参数β以及MCKD的滤波器长度L和故障冲击周期T分别表示种群中个体位置的四个坐标，设定β，f0，L，T的初始寻优范围；

4）以Morlet带通滤波预处理，进一步对预处理信号进行MCKD带内去噪后得到信号的CK最大作为衡量指标，采用NGA同步优化Morlet小波及MCKD参数；

5）取上一步获得最优个体中f0，β作为最优Morlet小波滤波参数对原始信号进行带通滤波，取最优个体中L，T对滤波信号进行MCKD带内降噪处理；

6）最后利用MCKD带内降噪后信号的包络谱判断是否有故障及故障类型。

2 仿真信号分析

在轴承实际运行时，所采集的振动信号中除了含有轴承自身的故障冲击及噪声外，可能还会受到外界其他偶然性冲击干扰影响。干扰冲击可由人为因素造成也有可能由机械设备中其他部件造成。偶然性冲击在振动信号中往往表现为幅值突然增大，冲击幅值一般可以达到轴承故障冲击的几倍，且不具有周期性，其存在易影响最终的解调分析结果。本小节对该情况下的振动信号进行分析。滚动轴承故障仿真信号x（t）为

式中x(t)的第一部分表示轴承局部故障引起的周期性瞬态冲击，Ai为具有一定周期时间的调幅信号，A0为幅值，si为轴承-传感器系统的脉冲响应函数，T表示两个瞬态脉冲之间的时间间隔，Bi为阻尼系数，fn为系统的固有频率，τi为时间延迟；x(t)的第二部分用来表示偶然性冲击干扰；n(t)为高斯白噪声，Q为幅值调制分量的频率；φA，φw，CA分别表示调幅分量的初相位、偶然性干扰冲击分量的初相位、常数偏差。

采用仿真信号对所提方法进行分析验证。内圈仿真信号如图3所示，其中内圈故障特征频率（BPFI）为90 Hz，外圈故障特征频率（BPFO）为80 Hz，滚动体故障特征频率（BPFB）为75 Hz，信号采样频率为20480 Hz，轴承结构共振频率为3500 Hz。为了使仿真信号更接近轴承实际运转时所产的振动信号，在内圈故障冲击信号中加入幅值为0.4 m/s2的高斯随机噪声，加入噪声后的时域波形如图3（b）所示。进一步在信号1000到1060点范围内人为添加一段幅值为10 m/s2、频率为1500 Hz的正弦振动信号如图3（c）所示，可见内圈故障冲击在正弦冲击干扰下已无法明显辨识。图3（d）为内圈仿真信号的包络谱，由图可以看到，从包络谱中不能找到有效的故障特征频率成分。

图3 内圈故障仿真信号Fig.3 Simulation signal of inner race fault

为了使本文所提方法的实验结果更具有说服力，首先采用谱峭度方法（Kurtogram）对图3（c）所示仿真信号进行对比分析，设置分解层数为3，得到的谱峭度图如图4（a）所示。最佳滤波频带的中心频率为1900 Hz，带宽为800 Hz。恰好涵盖了特意加入的正弦干扰冲击频率1500 Hz，显然Kurtogram受到了正弦干扰冲击的影响，滤波后信号的包络如图4（b）所示，包络谱图4（c）中没有明显的故障特征频率成分，无法判断滚动轴承是否存在故障。这是由于峭度指标未考虑故障冲击的周期性，在高幅值冲击的干扰下，导致滤波频带选择错误，最终Kurtogram方法诊断失败。

图4 内圈仿真信号谱峭度分析结果Fig.4 Results on simulation signal using Kurtogram

采用本文方法对仿真信号进行分析，设置NGA算法中迭代次数为100，种群规模20。根据内、外圈以及滚动体故障特征频率计算MCKD参数T，设置其寻优范围为［220，280］，并设置参数L，f0，β的寻优范围。最优个体对应的Morlet小波滤波器的中心频率f0=4000 Hz，带宽β=900 Hz，周期T=224，滤波器长度L=1373。滤波器窗口如图5（a）红色虚线所示，较好地覆盖了信号共振频率，且有效避开了加入的正弦干扰冲击频率1500 Hz，证明了该方法对偶然性冲击干扰具有良好的鲁棒性。利用该组参数对原始信号进行带通滤波以有效抑制故障信号中干扰脉冲成分，并采用MCKD对滤波后信号进行带内解卷积进一步突出故障冲击成分，处理后信号如图5（b）所示，图5（c）包络谱中89.6 Hz频率成分与内圈故障特征频率非常接近，且存在明显的倍频成分，可以判断此时轴承发生了内圈故障。因此仿真信号分析结果验证了本文方法在轴承振动信号特征提取中的可行性。

图5 本文所提方法分析结果Fig.5 Results of the proposed method

本文方法的创新点在于同步优化前后处理步骤算法重要参数，同时以能够有效衡量故障瞬态冲击周期性发生特点的CK作为优化准则，这是与目前大多数文章明显的区别。为了进一步证明本文提出方法的优势所在，采用Morlet-MED与本文方法进行对比分析。图6（b）为MED带内去噪后的时域波形，可以发现去噪后的信号中已无明显的冲击成分。在包络谱图6（c）中没有发现明显的故障特征频率成分，无法判断滚动轴承是否存在故障。故此方法诊断失败，且印证了本文所提方法的必要性。

3 实验数据分析

3.1 含偶然性冲击的实验信号分析

实验信号来自图7所示自制转子-轴承故障模拟试验台，该试验台可以模拟不同故障状态轴承振动及转子振动。试验台包括电机、控制器、支撑轴承、圆盘、轴承座、加速度传感器、计算机以及NI采集卡，振动信号由加速度传感器采集并保存在计算机中。试验所用轴承型号为N205，为了模拟轴承实际剥落故障，采用线切割技术在轴承外圈加工出宽度为0.5 mm的凹槽。试验过程中电机转速为1000 r/min，加速度传感器安装在轴承座正上方，图7已标出，采样频率为12 kHz。根据轴承各元件故障频率计算公式得到此时试验轴承外圈故障特征频率为BPFO=87.51 Hz，内圈故障特征频率为BPFI=129.15 Hz，滚动体故障特征频率为BPFB=41 Hz。

轴承外圈故障信号时域波形如图8（a）所示，时域波形中故障冲击成分较为明显，因人工加工凹槽较为标准，导致故障冲击幅值较大。为了使所采集的振动信号更加接近轴承在复杂工况下真实的振动信号，在所采集的信号基础上添加幅值为4 m/s2的高斯随机噪声，加入噪声后信号如图8（b）。为了模拟外界偶然冲击干扰，在信号中2281到2360点范围内人为添加一段幅值为60 m/s2的随机振动，如图8（c）所示。从图8（c）中可以看出，偶然性冲击幅值远大于轴承故障冲击幅值，偶然性冲击在振动信号中占绝对优势，轴承外圈故障特征在此干扰冲击下已经无法准确被识别。

为了表明本文所提方法更具说服力，首先采用Kurtogram对图8（c）仿真信号进行分析，设置分解层数为3，得到谱峭度图如图9（a）所示。最优个体对应的最佳滤波频带参数中心频率为5625 Hz，带宽为750 Hz。滤波后信号包络如图9（b）所示，包络谱图9（c）中没有明显的特征频率成分，因而无法判断滚动轴承是否存在故障，故Kurtogram方法诊断失败。

图9 实验室信号原始谱峭度分析结果Fig.9 Results on laboratory signal using original Kurtogram

采用本文所提方法所得分析结果如图10所示，设置NGA算法中迭代次数为100，种群规模20。根据内、外圈以及滚动体故障特征频率计算MCKD参数T并设置寻优范围为［75，300］。得到最优Morlet小波滤波器的中心频率f0=3500 Hz，带宽β=800 Hz，周期T=137，滤波器长度L=1301。Morlet滤波器窗口如图10（a）红色曲线所示。进而利用该组参数对原始信号进行滤波以消除干扰脉冲的影响，并对滤波后信号进行MCKD带内解卷积以进一步突出周期性故障冲击，得到图10（b）最终滤波信号中存在明显的周期性冲击脉冲，其包络谱图10（c）中88 Hz频率成分与外圈故障特征频率87.51 Hz非常接近，且存在176和263 Hz等明显倍频成分，可以判断此时轴承发生了外圈故障。背景噪声以及干扰冲击得到有效抑制，所产生的偏差可能是由于转速波动及轴承内部元件打滑造成。实验信号分析表明本文所提方法在自制转子-轴承故障模拟试验台信号分析中具有可行性。

图10 本文所提方法分析结果Fig.10 Results on using the proposed method

为了进一步证明本文提出方法的优势，利用Morlet-MED方法对图8（c）的信号进行分析，结果如图11所示。图11（b）的MED带内去噪后的时域波形中发现去噪后信号已无明显的冲击成分。包络谱图11（c）中没有明显的故障特征频率成分，无法判断滚动轴承是否存在故障。故此方法诊断失败，更加印证了本文所提方法的必要性。

图11 对比方法分析结果Fig.11 Results using Morlet filter and MED

3.2 COINV实验数据分析

信号来自于东方所的COINV-1618型传动系统典型故障模拟实验台，如图12所示。该试验台可以模拟不同故障状态轴承、齿轮振动及转子不平衡振动。试验台由底座、直流电机、齿轮箱、滚动轴承、数显式调速器、圆盘、轴承座、加速度传感器等组成，振动信号由加速度传感器采集并保存在计算机中。试验所用滚动球轴承型号为6200 Z，滚珠数8个，故障形式为轴承内圈有一处断裂。转轴转速为1000 r/min。加速度传感器安装在轴承座正上方，采样频率为19692.3 Hz。根据轴承各元件故障频率计算公式计算得到此时试验轴承内圈故障特征频率为BPFI=75 Hz，外圈故障特征频率为BPFO=67.75 Hz，滚动体故障特征频率为BPFB=58 Hz。

图12 滚动轴承故障实验台Fig.12 Test rig for bearing fault detection

采用本文所提方法所得分析结果如图13所示，设置NGA算法迭代次数为100，种群规模20。根据内、外圈以及滚动体故障特征频率计算MCKD参数T并设置其寻优范围为［230，350］。原始信号如图13（a）所示，最优个体对应的Morlet小波滤波器的中心频率f0=7200 Hz，带宽β=500 Hz，周期T=262，滤波器长度L=1220。滤波器窗口如图13（b）红色曲线所示。利用该组参数对原始信号进行滤波，并对滤波后信号进行MCKD带内二次去噪，结果如图13（c）所示，可以看到存在明显周期性冲击脉冲。图13（d）的包络谱中可以看到75.4 Hz的频率成分与外圈故障特征频率75 Hz非常接近，且存在154.3和229.7 Hz等明显倍频成分，可以判断此时轴承发生了外圈故障，背景噪声得到有效抑制。因此本文所提方法在INV-1618型传动系统典型故障模拟实验台的信号分析中具有可行性。

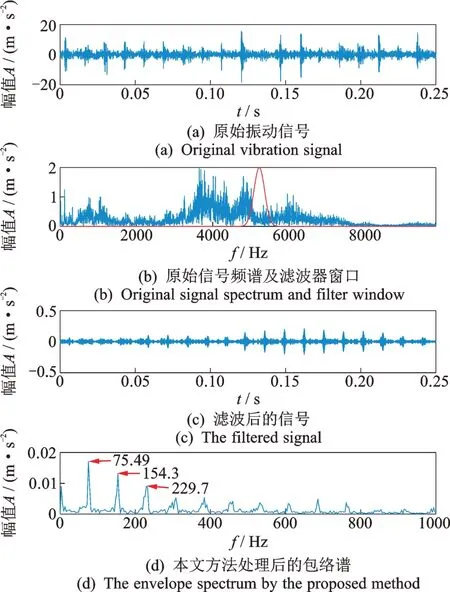
图13 本文所提方法分析结果Fig.13 Results using the proposed method

4 结论

针对共振解调方法共振频带难以确定、存在带内噪声残余以及偶然性冲击干扰等问题，提出了一种由Morlet小波滤波和MCKD构成的复合诊断方法，前者用于滤除大部分噪声，后者用于消除带内残余噪声。以小生境遗传算法为优化手段，相关峭度为适应度函数，对Morlet滤波器和MCKD的参数进行同步自适应优化。仿真信号、实验室信号以及东方所实验数据表明：

（1）对带通滤波及带内二次消噪参数进行同步优化，以二次滤波信号的相关峭度最大为准则，可以有效消除外界高幅值偶然性冲击影响并减小信号传输路径和噪声干扰，保证了故障诊断的有效性；

（2）合理设置Morlet小波的中心频率、带宽及MCKD周期T、滤波器长度L的取值范围，采用NGAs优化算法有效解决了滤波器共振频带难以确定、MCKD存在重要参数故障周期需要预先设置的问题，使前后处理算法的效果得到了保障；

（3）小生境遗传算法可以保持解的多样性，避免陷入局部最优解，且同时具有很高的全局寻优能力和收敛速度、鲁棒性高，为快速实现滚动轴承故障诊断提供有益参考及方法补充。为突出本方法的优越性，将本方法与谱峭度、Morlet-MED诊断方法作对比分析，结果表明所提方法诊断效果更具优势。