扭弯频率比对π型断面节段模型后颤振特性的影响
2022-01-12张志田汪志雄谭卜豪
张志田,汪志雄,郄 凯,谭卜豪
(1.海南大学土木建筑工程学院,海南 海口570228;2.湖南大学土木工程学院,湖南 长沙410082;3.广东省交通规划设计研究院股份有限公司,广东广州510507)
引言
桥梁颤振稳定一直是研究热点,众多学者采用线性理论对这一问题进行了广泛的研究[1-5]。线性理论表明,来流风速超过颤振阈值后桥梁会出现振幅发散形式的动力失稳现象。然而,大振幅下的非线性气弹效应可能促使桥梁发生极限环振动而不是发散振动。极端天气出现的概率逐年增加[6],一些颤振稳定性较低的桥梁有可能进入颤振后状态。如美国的原塔科马桥在较低风速下出现了大幅振动并最终坍塌,而美国的金门大桥同样经历了颤振却得以幸存[7]。由此可知,不同气动外形有不同的后颤振性能。如果在设计阶段就考虑桥梁的后颤振性能,并尽可能降低其后颤振幅值,则能提高其颤振失稳后的幸存概率,增加其抗风强健性。因此,研究桥梁的后颤振气动性能是必要的。
目前,研究颤振响应特性最直接的方法是风洞试验。朱乐东、高广中发现了典型桥梁断面存在不同尺度的软颤振现象[8]。郑史雄等研究了π型断面的软颤振特性[9],并通过气动措施对软颤振进行抑制。Daito等研究的π型及H型断面同样出现了软颤振现象[10],且不同断面的软颤振特性差异较大。Amandolese等也通过微型风洞研究了矩形平板断面弯扭耦合颤振的幅值、频率以及阻尼特性[11];Zhang等通过风洞试验对箱梁断面的软颤振性能进行了研究,研究表明箱梁断面为弯扭耦合颤振[12]。另外,实际桥梁和风洞试验均存在几何与阻尼非线性,从而使结构进入极限环状态。吴长青、张志田数值研究结果表明,考虑几何非线性之后平板断面也可进入后颤振状态[13]。以上文献主要针对某一组动力特性下桥梁断面的后颤振性能进行研究,然而同种断面形式可用于不同跨径的桥梁。不同跨径桥梁的节段模型主要体现在扭弯频率不同。目前缺少针对不同扭弯频率比节段模型的后颤振研究。文献[14]中对扭弯频率比的应用也只体现在颤振临界风速上。
π型主梁断面在大跨径桥梁中得到了广泛应用[15-16]。本文针对某一大跨径斜拉桥的π型主梁断面,采用弹性悬挂节段模型风洞试验,研究了不同扭弯频率比下的颤振阈值以及后颤振响应特性,并分析了在后颤振状态下的幅值、频率、相位以及动态频率和阻尼随时间演变的特性。
1 风洞试验
1.1 试验设置
试验所采用的π型断面如图1所示。节段模型通过弹性悬挂装置固定于风洞中,如图2所示。设置两块倒角椭圆形端板以减少端部三维风场效应。节段模型采用不锈钢边主梁以及6061T硬铝桥面板作为框架保证整体刚度。桥面铺装层、横梁以及栏杆附属设施采用ABS板制作确保气动外形。模型的竖向刚度(Kv)由8根竖直弹簧提供;扭转刚度(Kt)通过设弹簧悬挂点的顺风向距离来模拟。
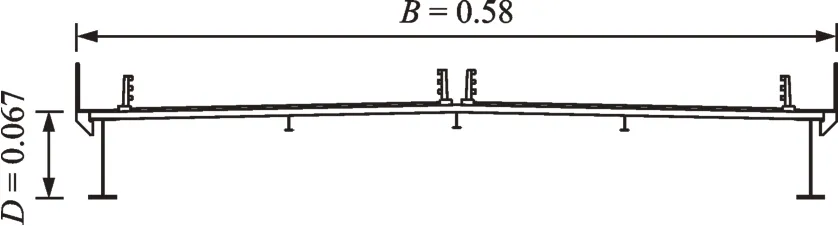
图1 模型标准断面(单位:m)Fig.1 Standard model section(Unit:m)

图2 节段模型风洞试验悬挂Fig.2 The segment model mounted in wind tunnel
成桥状态设计参数以及通过相似比(1∶50)换算的节段模型设计参数如表1所示。从表1中可知节段模型的扭转和竖弯频率之比ft/fv=1.035,这种情况下可能发生弯扭耦合振动。为进一步研究ft/fv对后颤振耦合响应特性的影响,在确保竖向频率基本不变的前提下设置不同ft/fv的五种工况,分别为0.872,0.971,0.988,1.085以及1.245。试验采用两个单点位移计进行模型竖向和扭转响应测量,两个位移计相距290 mm。位移采集频率为200 Hz。每级风速采集时间大约为60 s。改变风速后隔2-3 min再次采集。所有工况的初始攻角为+3°,且来流条件为均匀流。测试过程中无任何初始激励。
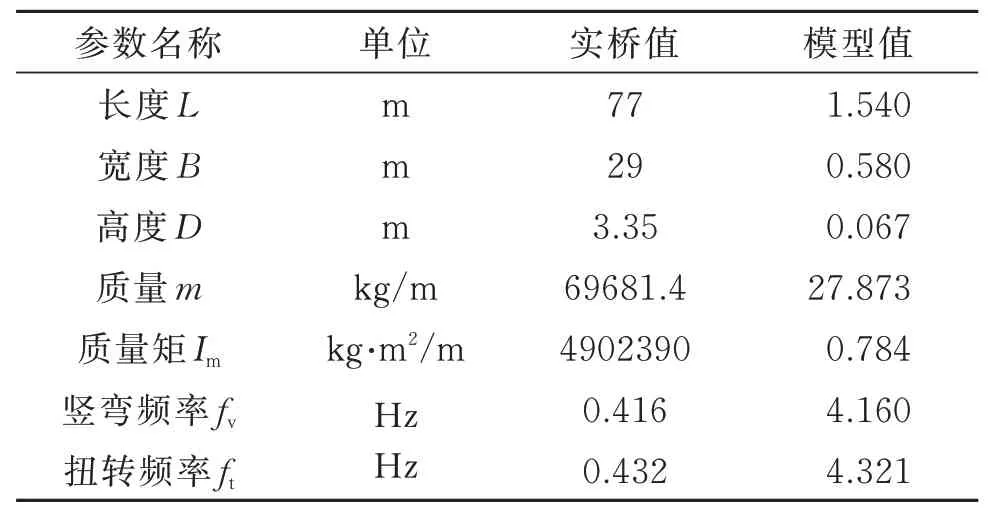
表1 实桥及节段模型设计参数Tab.1 Design parameters of the prototype and segment model
ft和fv通过自由衰减振动时程曲线做频谱分析获得,其质量(m)和质量矩(It)由下式计算:
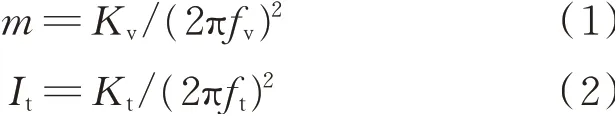
式中m为悬挂系统等效质量;Kv为弹性悬挂系统竖向刚度,具体为29309.6 N/m;fv为悬挂系统竖向固有频率。It为悬挂系统等效质量矩;Kt为弹性悬挂系统扭转刚度,其计算公式为;Kt=Kv×(xsc)2,xsc为弹簧悬挂点距模型剪心距离;ft为悬挂系统扭转固有频率。
各个工况弹性悬挂模型参数如表2所示。
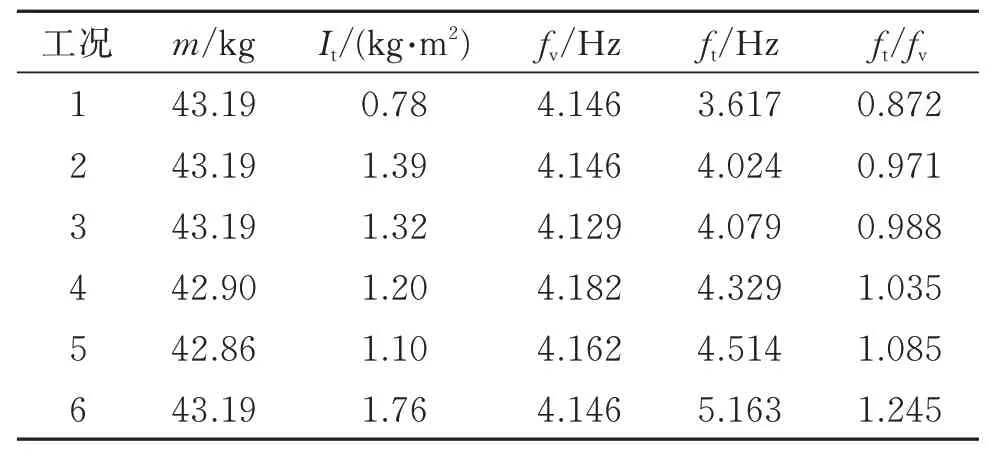
表2 不同扭弯频率比的弹性悬挂模型参数Tab.2 Parameters of the elastically mounted model with different torsion-bend frequency ratios
1.2 弹性悬挂系统非线性特性
大振幅下弹性悬挂系统的阻尼和刚度会体现出非线性特性。为了进一步研究弹性悬挂系统非线性阻尼对颤振后状态的影响,采用零风速下大振幅的自由衰减振动识别系统的非线性阻尼,识别方法参考文献[17]。这里仅给出ft/fv=0.872模型的自由衰减时程(如图3所示)及对应的阻尼和频率随幅值演变的结果,如图4所示。从图中可知,扭转阻尼均有明显的非线性特性,而竖向阻尼随幅值变化较弱。根据作者目前的研究,竖向阻尼非线性特性较弱可能是弹簧刚度较大引起的。

图3 自由衰减时程Fig.3 The free decay time histories
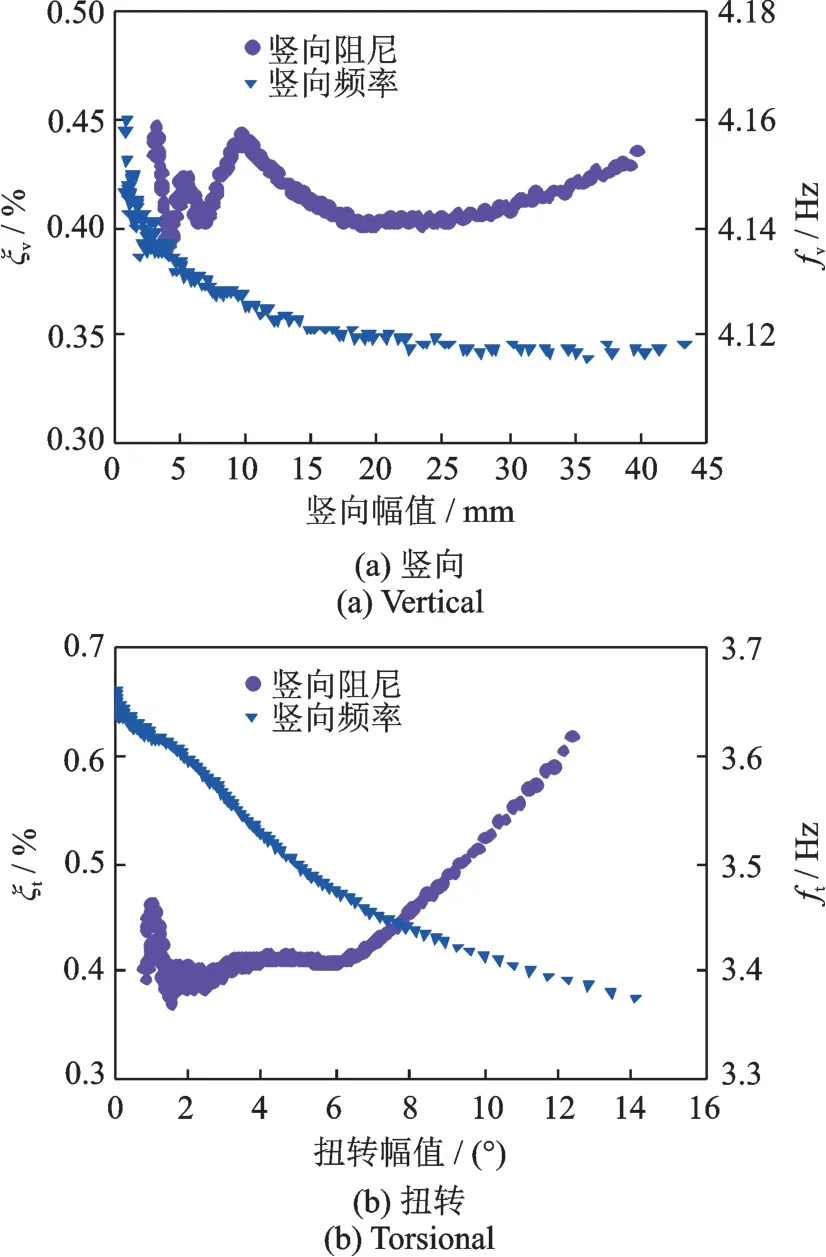
图4 弹性悬挂系统的非线性特性(ft/fv=0.872)Fig.4 Nonlinear properties of the suspended elastic system with ft/fv=0.872
2 耦合颤振响应特性
2.1 颤振响应幅值
颤振幅值结果如图5所示。从图中可知,所有工况在颤振临界风速之后都进入了极限环状态,其振动的形式为弯扭耦合颤振。由前面讨论可知,系统具有阻尼、几何以及气动非线性特性,这些都可能促进极限环的形成。鉴于后颤振状态下模型的竖向和扭转均为简谐振动,采用如下形式描述极限环振动
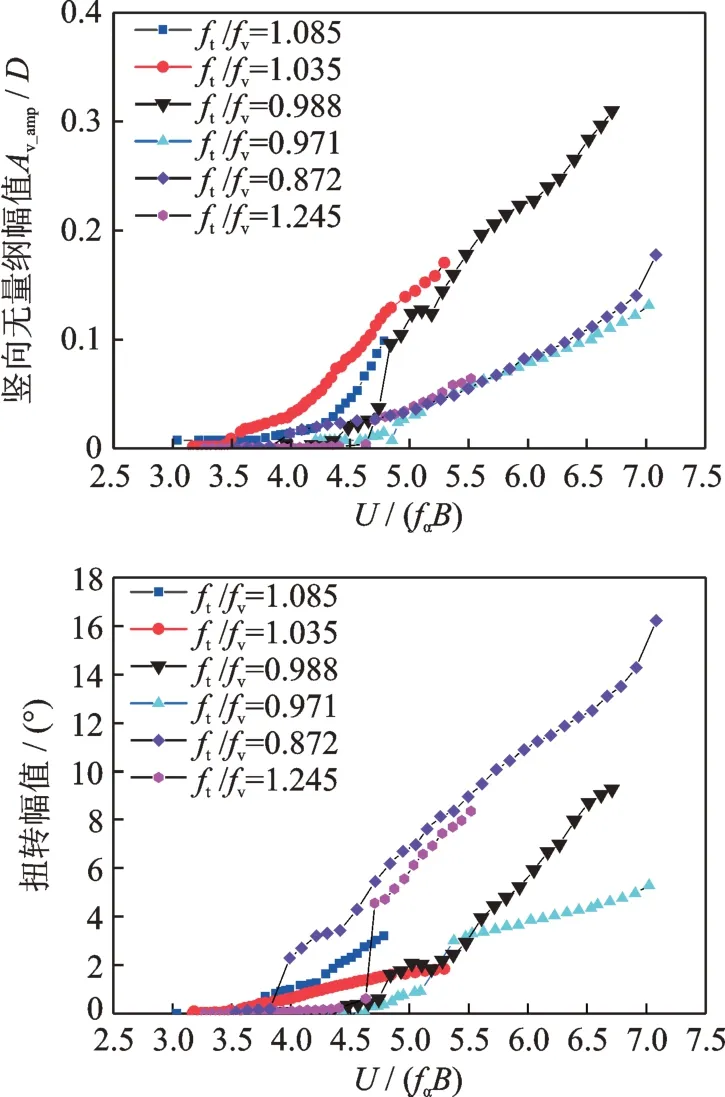
图5 颤振极限环幅值Fig.5 The amplitude of LCO

式中Ai(i=h,α)为竖向或扭转响应位移;Ai_0(i=h,α)为竖向或扭转响应均值;Ai_amp(i=h,α)为竖向或扭转响应幅值;fi(i=h,α)为竖向或扭转响应主频;φi(i=h,α)为竖向或扭转响应初相位;t为时间。
后颤振状态下的竖向和扭转幅值均随风速增大,但随风速演变的趋势相差较大。当来流风速超过颤振临界风速后,ft/fv=0.872和ft/fv=1.245的竖弯和扭转的幅值分别在U/(fαB)为3.99和4.71处有突变点,尤其是扭转幅值,具有硬颤振特点(超过颤振临界风速之后幅值突然增大)。值得注意的是,两种情况下扭弯频率比不同所形成的无量纲颤振临界风速差异达到20%以上。对比图中各工况的结果可知,扭弯频率比不仅可以改变颤振的软硬性质,同时对颤振临界风速(如图6所示)、扭转与竖弯运动的耦合程度、后颤振极限环幅值(同一风速下可达数倍以上的差距)、极限环幅值的演变路径都有显著的影响。

图6 不同频率比的颤振临界风速Fig.6 Critical wind speed for different frequency ratios
规范[14]计算的颤振临界风速与试验的相对误差(Res)定义如下
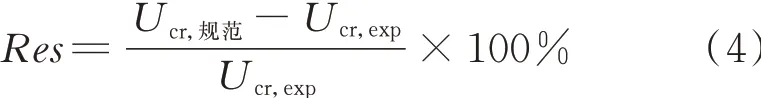
在规范[14]中,颤振临界风速的计算源于理想平板的气动力理论,其表达示如下
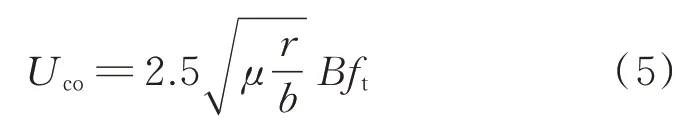
式中Uco为平板颤振临界风速;B为主梁特征宽度;b为特征宽度的一半,b=B/2;μ为桥面单位长度的质量与空气密度比,μ=m/(πρb2),其中ρ为空气密度;r为惯性半径为扭转基频。

式中ε为扭弯频率比,ε=ft/fv;ωv=2πfv。

式中ωt=2πft;μˉ为空气与桥面的密度比,μˉ=1/μ;

最终桥梁断面的颤振临界风速通过断面形状系数和攻角效应系数修正的如下所示式中ηs为形状系数,取值为0.4;ηα为攻角修正系数,取值为0.85;Uco源于式(5),(6)及(7)。
基于式(5)和(6)计算的π型断面的颤振临界风速如图7所示。从图中可知,基于公式(6)计算的颤振临界风速的结果比公式(5)更靠近试验值,基于公式(5)计算的颤振临界风速最大相对误差达149.34%,其他工况的相对误差如图8所示。公式(5),(6)以及(7)都不能对ft/fv=1.035和ft/fv=1.085的颤振临界风速比ft/fv=0.971和ft/fv=0.988要低的情况做出合理的解释,表明了目前规范[14]的不足。

图7 规范计算的颤振临界风速Fig.7 Critical flutter wind speed calculated by specification
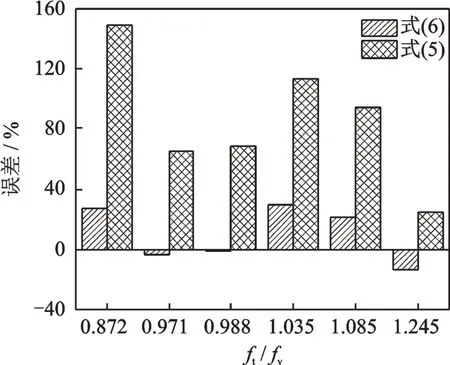
图8 相对误差Fig.8 Relative errors
为了进一步研究竖向振动的参与程度,定义了无量纲系数竖向相对扭转幅值系数η,简称竖扭幅值系数,其表达式如下
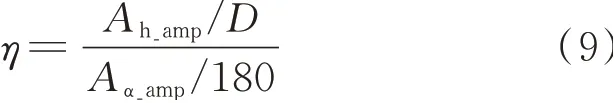
所有工况的η随风速演变规律如图9所示。从图中较容易得知ft/fv=0.872和ft/fv=1.245的η系数较小且随风速增长缓慢,这说明了后颤振主要为扭转振动。ft/fv越接近1,η系数值越大,尤其是ft/fv=1.035和ft/fv=1.085,η系数随风速增长速率相对于其他工况大,也就是说竖向振动参与程度大。
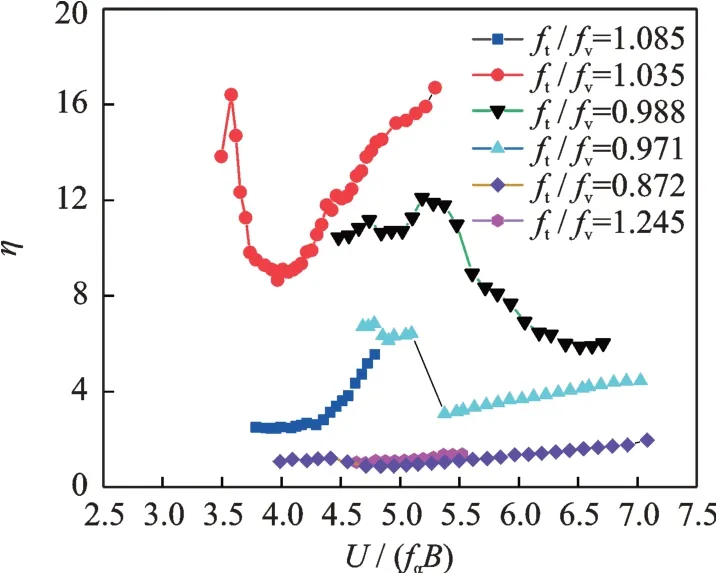
图9 系数η随风速演变图Fig.9 η coefficients versus wind speed
2.2 颤振位移时程及频率特性
2.2.1 颤振位移时程
图10给出了ft/fv=0.872时六种风速下的竖向和扭转位移时程。从图中可以得知,当来流风速为U=7.82 m/s,扭转响应已近接近单一频率,但幅值没有完全稳定,而竖向响应没有明显的规律可循。当风速超过颤振临界风速后,节段模型进入极限环状态,其竖向和扭转响应有一定程度耦合,但两者存在相位差。

图10 后颤振时程响应(ft/fv=0.872)Fig.10 The time history of post-flutter for ft/fv=0.872
2.2.2 颤振频率特性
耦合振动频率随风速的演变规律如图11所示。从图11中可知,所有工况的耦合频率都随风速降低。ft/fv=0.872和ft/fv=1.245的模型频率在整个后颤振风速区间内降低较为平稳;ft/fv=0.971,ft/fv=0.988,ft/fv=1.035以及ft/fv=1.085的模型耦合频率在风速较低时靠近扭转基频。ft/fv=0.988和ft/fv=

图11 后颤振耦合频率随风速演变图Fig.11 The evolutions of coupled frequency of post-flutter with wind speed
1.085的模型在高风速区耦合频率随风速降低的速率增大。ft/fv=0.971的模型耦合频率在后颤振过程中有明显的突变点。ft/fv=1.035的模型耦合频率随风速演变有接近平稳的趋势,这可能是悬挂系统阻尼随极限环幅值增大而增大引起的。ft/fv=1.245,ft/fv=1.085以及ft/fv=1.035的模型耦合主频率在竖向和扭转固有频率之间;ft/fv=0.988,ft/fv=0.971以及ft/fv=0.872的模型耦合主频率低于竖向和扭转中的任何一个固有频率,说明受气动负刚度的影响,系统的扭转频率始终是下降的。
竖向和扭转响应的频谱特性更能直观地体现耦合频率成分,图12中给出了ft/fv=0.872的模型六种不同风速下竖向和扭转响应FFT的频率成分,其横坐标分辨率大约为0.015 Hz。从图中可以得知,当来流风速低于颤振临界风速时,竖向和扭转响应的频率成分较多,其主要频率也不相同,表明了竖向和扭转还没有进入耦合模式。当来流风速超过颤振临界风速后,竖向和扭转响应的频率基本相同。在风速较低的情况下,倍频成分不明显;当风速高于11.7 m/s时,有轻微倍频成分存在,但在整个频率成分中所占比例很小,这和文献[18]研究的扁平箱梁高次谐波分量显著存在较大的差异。

图12 后颤振频率特性(ft/fv=0.872)Fig.12 Frequency properties of post-flutter for ft/fv=0.872
2.3 耦合特性
耦合振动有两种模式,一种如图13(a)所示,旋转中心靠前,另一种如图13(b)所示,旋转中心靠后。
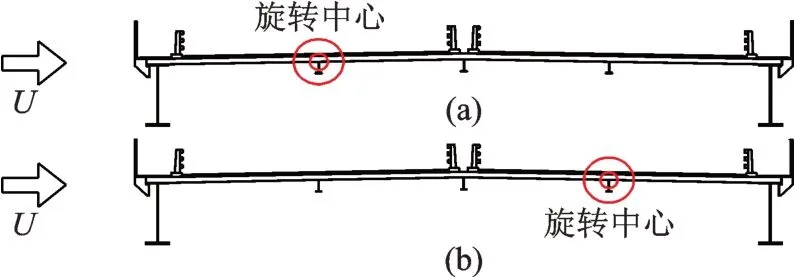
图13 耦合振动模式示意图Fig.13 Schematic diagram of coupled vibration patterns
耦合振动的模式取决于扭转和竖向振动的相位差φα-φh。图14给出了不同频率比的模型在后颤振状态下φα-φh随风速演变的规律,从图中可知所有工况的φα-φh随风速增加。ft/fv=1.035和ft/fv=1.085的φα-φh随风速增长最快,也是在六种工况中相位差发生正负号变化的两种工况,且没有明显趋于 稳 定 的 迹 象。ft/fv=0.872,ft/fv=0.971,ft/fv=0.988以及ft/fv=1.245的φα-φh随风速增加缓慢,且慢慢趋于稳定的值。文献[11]的研究结果表明耦合颤振时相位差φα-φh会趋于0。文献[19]的研究结果也表明,对于耦合颤振,当竖向与扭转振动的相位差为零时才能使得结构从气流中吸收的能量最大化。图14显示的结果显然与文献[11,19]的结论均有实质性的差异,这种非零相位差的现象引发一个基本问题,即π型断面颤振时自由度的耦合现象可能不是颤振的原因,而是分离流颤振后能量转移的结果,这一问题仍有待深入研究。
2.4 颤振动力响应分析
为了更直观地研究在整个颤振响应过程中瞬态阻尼的变化趋势,采用如下的阻尼计算公式[20]

式中ξi(i=h,α)为竖向或扭转瞬态阻尼;fi(i=h,α)为竖向或扭转瞬态频率;Ai_amp(i=h,α)为竖向或扭转瞬态幅值。
图15给出了阻尼和频率随时间演变的规律。从图中可以得知,ft/fv=0.872和ft/fv=1.035模型振动的阻尼以及频率随时间的演变存在较大的差异。ft/fv=0.872模型的扭转频率随时间基本平稳减小,而ft/fv=1.035模型的频率演变存在较大的波动,需经过较长的时间才趋于稳定。这两者的竖向和扭转阻尼在颤振发展的过程中存在明显的差异,这可能是引起后颤振极限环幅值差异大的原因。
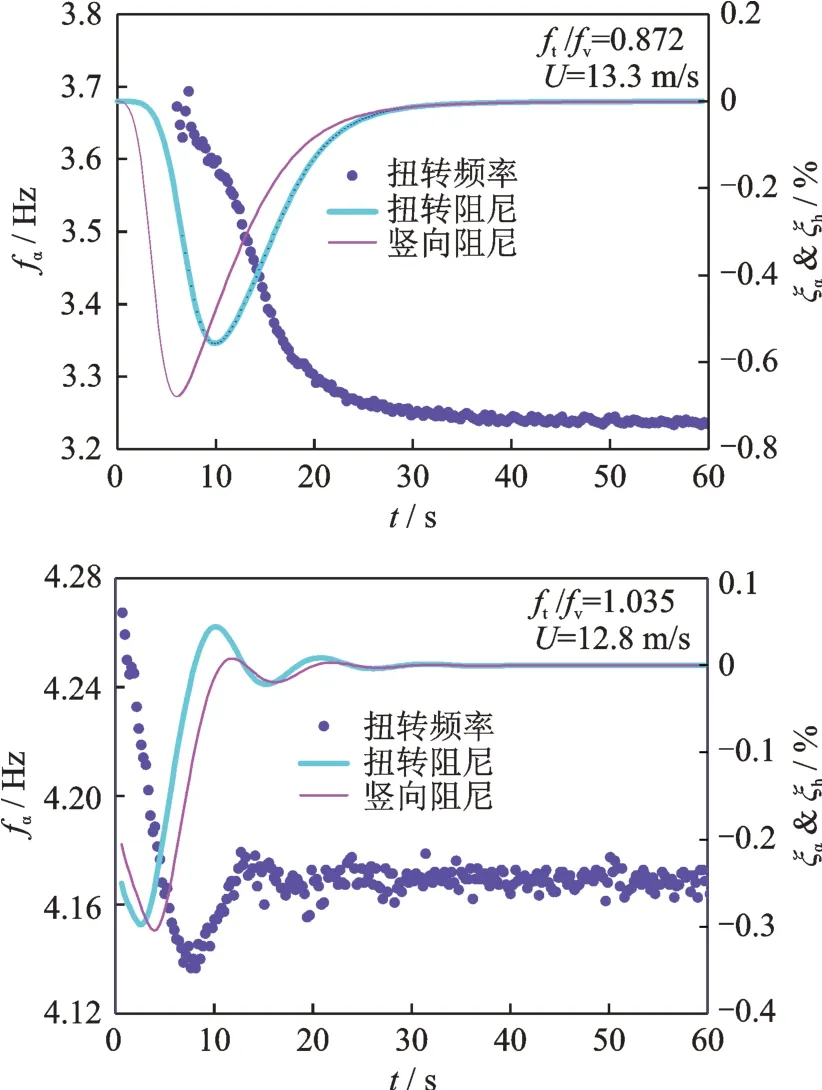
图15 扭转频率及气动阻尼随时间演变图Fig.15 The time history of frequencies and damping ratios
3 结论
1)扭弯频率比对π型断面的颤振基本特性有实质性的影响,包括临界风速、极限环幅值、颤振幅值随风速的演变路径、竖向与扭转运动的耦合程度、两耦合自由度之间的相位差,甚至“软”、“硬”颤振性质都受其影响。
2)将文献[14]中提供的颤振阈值计算公式应用到本文所研究的断面时,最大误差可达到149.34%,且不能解释不同扭弯频率比带来的差异。
3)π型断面的颤振发展过程中阻尼具有显著的幅值依赖性;颤振发展过程中竖向和扭转阻尼的演变对最终的颤振极限环幅值产生较大的影响。
4)耦合颤振特征之一是,自由度之间的耦合是颤振的必要条件。π型断面的颤振试验现象表现为弯扭耦合形式,但该耦合是形成颤振的必要条件,还是分离流扭转颤振激发后竖向振动被动参与,仍有待深入研究。
