OFDM 中一种有效的基于分段非线性压扩的PAPR 抑制算法

邢智童，李云，彭德义，张本思，刘凯明，刘元安

（1.重庆邮电大学移动通信技术重庆市重点实验室，重庆 400065；2.北京邮电大学智慧无线移动信息技术研究中心，北京 100876）

1 引言

正交频分复用（OFDM,orthogonal frequency division multiplexing）在5G/B5G/6G 等现代和未来通信系统中有着良好的应用前景[1]。然而，OFDM系统的一个较大的缺陷是它的峰均比（PAPR,peak-to-average power ratio）较高。较高的PAPR 使OFDM 信号样点在经过了功率放大器以后，面临较大的非线性失真；同时使OFDM 信号样点在经过了非线性功率放大器以后，面临较大的误比特率（BER,bit error rate）。因而，研究OFDM 系统的PAPR 抑制是一个十分重要的问题。在5G/B5G/6G等现代和未来通信的场景下，PAPR 的抑制变得更加重要。一方面，随着毫米波[2]的引入，5G/B5G/6G通信的传输会使用更多的子载波数目，从而进一步加大OFDM 系统的PAPR。另一方面，在5G/B5G/6G通信的传输中，基站能耗较大的问题依旧存在[3]，这导致如果OFDM 信号样点的PAPR 过高，则必须进行一定的功率回退[4]，这将大大降低功率放大器的效率。故而，在面向5G/B5G/6G 等现代和未来的宽带无线通信系统中，降低PAPR、提高功率放大器效率的需求同样迫切。

为了降低OFDM 系统的PAPR，目前已有大量的文献研究，这些PAPR 抑制算法大致可以分为三大类[5]。1) 以降低大幅度信号出现的概率为主体的概率类算法，如选择映射序列、部分传输序列等算法。2) 以编码技术为主体的算法，在这类算法中，信道编码技术，如卷积码、线性分组码、polar 码等被用于降低OFDM 系统的PAPR。3) 以信号预失真为主的压扩类算法，这类算法不改变OFDM 信号样点的相位，并使用相应的函数对OFDM 信号样点的幅度进行改变，从而抑制OFDM 系统的PAPR。这类算法包括限幅法[6]、线性压扩算法[7-11]和非线性压扩算法[12-22]。

在以上PAPR 抑制算法中，非线性压扩算法是一项非常有竞争力的算法，它们能够在PAPR 性能和功率频谱密度（PSD,power spectral density）性能之间实现平衡。

非线性压扩算法的一种思路是先将压扩后OFDM 信号样点的幅度满足的概率密度函数（PDF,probability density function）从瑞利分布改为一个有限概率分布，这样可以抑制压扩后OFDM 信号样点幅度的最大值。一般而言，将压扩后OFDM 信号样点幅度的最大值称为压扩后OFDM 信号样点幅度满足的PDF 的限幅点。在压扩后OFDM 信号样点满足的PDF 的参数设计中，需要确保PDF 的积分为1以及压扩后和压扩前OFDM信号样点的平均功率相等这2 个条件。文献[12]不对幅度较小的信号进行压扩处理，对幅度较大的信号，将压扩后信号样点幅度满足的PDF 从瑞利分布改为一个PAPR 较低的有限的PDF。该算法可以在有效降低OFDM 信号样点的PAPR 的前提下，确保压扩函数失真较低，从而确保压扩后OFDM 信号样点的BER 性能和PSD 性能。然而，文献[12]提出的算法由于强制要求压扩后OFDM 信号样点的概率分布密度函数在限幅点处的值为0，将影响压扩函数设计的灵活性。文献[13]提出了指数压扩（EC,exponential companding）算法。它将压扩后OFDM 信号样点满足的PDF 从瑞利分布改为均匀分布。该算法可以降低OFDM 信号样点的PAPR，并同时保证压扩后和压扩前OFDM 信号样点的平均功率相等。然而，该方法会对OFDM 信号样点产生较大的压扩失真，从而影响压扩后OFDM 信号样点的BER 性能和PSD 性能。然而，文献[13]在设计压扩后OFDM 信号样点满足的PDF 时，对大幅度的信号和小幅度的信号都进行了处理，这将在一定程度上产生不必要的压扩，从而提高压扩失真。文献[14]提出了一种基于瑞利分布和均匀分布相结合的分段非线性压扩算法。该算法不改变小信号样点的幅度，对于大幅度的信号，该算法将其压扩后对应的PDF 从瑞利分布改为均匀分布。文献[15]中的Wangs 算法不对幅度较小的信号进行处理，对于幅度较大的信号，将压扩后OFDM 信号样点幅度满足的PDF 从瑞利分布改为线性分布。文献[16]提出了一种基于平方根倒数结构（ISQR,inverse square root component）的分段非线性压扩算法。该算法不改变幅度较小的信号，对于幅度较大的信号，该算法将压扩后OFDM信号样点的幅度满足的PDF 从瑞利分布改为平方根倒数的分布。文献[17]提出了Perturbed 算法，该算法将压扩后OFDM 信号样点的幅度满足的PDF 从瑞利分布改为分段线性分布，这些分段线性函数可以良好地拟合瑞利分布函数。然后，在实际的传输中，还将对这些分段线性函数进行适当的扰动，以寻找最优的分段拟合函数。文献[18]设计了分段非线性压扩函数。该压扩函数不对幅度较小的信号进行压扩，对于幅度较大的信号，该压扩函数将压扩后OFDM 信号样点的概率分布密度函数从瑞利分布改为经过伸缩变换的瑞利分布，使压扩后OFDM 信号样点的PDF 是一个有限分布，且具有较低的失真。文献[19]将小幅度信号和大幅度信号分段进行处理，对于幅度较小的信号，将压扩后OFDM 信号样点的PDF 从瑞利分布改为一个经过伸缩变换的瑞利分布函数；对于幅度较大的信号，将压扩后OFDM 信号样点的PDF 从瑞利分布改为线性分布。

非线性压扩算法的另一种思路是直接设计非线性压扩函数。文献[20]提出了μ律压扩算法。然而，该压扩算法会提高OFDM 信号样点的平均功率，从而对OFDM 信号样点的PAPR 抑制效果产生影响。文献[21]设计了限幅压扩（ALC,amplitude limited companding）多项式的算法，抑制压扩后OFDM 信号样点的PAPR。文献[22]设计了分段非线性压扩函数降低OFDM 系统的PAPR。该算法不改变小幅度信号的幅度，对于大幅度信号，使用限幅的算法，使压扩后OFDM 信号样点的最大幅度不超过一个固定的值；对于中等幅度的信号，使用多项式函数对OFDM 信号样点进行压扩，弥补因为限幅导致的损失。

目前，压扩算法设计存在的问题是算法本身很难在PAPR 性能、BER 性能和计算复杂度之间达到平衡。因而，如何设计一种压扩算法，使压扩后OFDM 信号样点在确保低PAPR 传输的前提下，仍然保证较低的BER 是基于压扩变换的OFDM 系统的PAPR 抑制算法设计中十分重要的研究课题。

本文设计了一种基于通用瑞利和三角分布相结合的分段非线性压扩（GHRSDNC,generalized hybrid of rayleigh and sine distribution based nonlinear companding）算法。该算法不对小幅度信号进行压扩处理，对于大幅度的信号，该算法将压扩后OFDM 信号样点幅度满足的PDF 从瑞利分布改为三角函数分布。该算法在设计完压扩函数后，通过求解概率守恒以及压扩后和压扩前OFDM 信号样点的平均功率相等这2 个约束条件，求解出对应的压扩函数的参数的解析解。考虑到三角函数分布的图像在形状上与瑞利分布函数的图像接近，该压扩算法可以确保较低的压扩失真。此外，该压扩算法还可以通过灵活地调整参数，确保压扩算法在PAPR 和BER 之间达成平衡。本文相比于其他算法，如文献[12]的算法，更具有通用性。

2 基于压扩变换OFDM 系统模型

基于压扩变换的OFDM 系统的结构如图1 所示。在OFDM 系统中，宽带信号被划分为N个不同的子载波。经过正交移相键控（QPSK,quadrature phase shift keying）或者正交振幅调制（QAM,quadrature amplitude modulation）后的信号独立地传输于每一个子载波上。假设第k个子载波（0≤k≤N-1）上的信号为Xk，则OFDM 系统对这N路子载波上的数据进行快速傅里叶逆变换（IFFT,inverse fast Fourier transform）处理。在输出端，第n个（0≤n≤N-1）子载波上的信号为

图1 基于压扩变换的OFDM 系统的结构

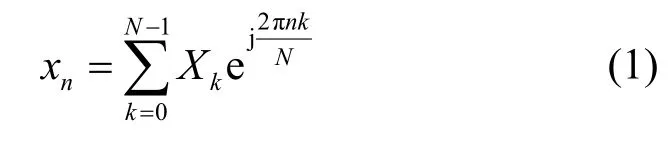
OFDM 信号的峰均比被定义为N个输出信号中，峰值信号和平均信号功率的比值，记作

由中心极限定理可知，当子载波数目N足够大时，OFDM 时域信号样点xn满足正态分布。相应地，时域信号样点xn的幅度|xn|满足的PDF 为瑞利分布，记作

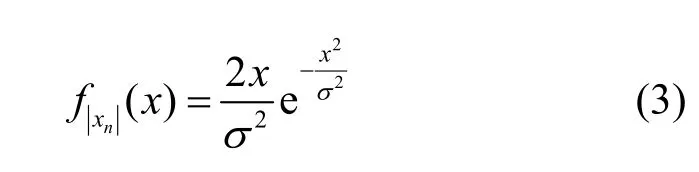
其中，σ2表示的是OFDM 信号样点的平均功率。相应地，瑞利分布函数的PDF 对应的累计分布函数（CDF,cumulative distribution function）为

如果使用压扩算法抑制OFDM 信号样点的PAPR，一种常见的思路为将压扩后OFDM 信号样点的概率分布从瑞利分布改为一个PAPR 较低的PDF，然后根据压扩后的概率分布，推导出对应的压扩函数的表达式。假设压扩后OFDM 信号样点幅度满足的PDF 为对应的CDF 为则对应的压扩函数的表达式为

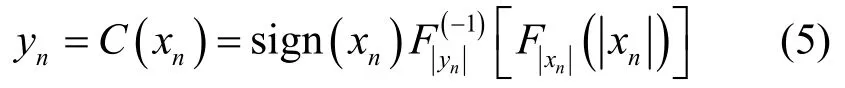
3 分段非线性压扩算法

压扩函数的设计基于将压扩后OFDM 信号样点幅度满足的PDF 从瑞利分布改为一个PAPR 较低的PDF，然后根据压扩后和压扩前OFDM 信号样点的概率分布，推导出压扩函数。

在压扩函数的设计中，假设压扩后的信号样点为yn，压扩后OFDM 信号样点满足的PDF 为考虑到压扩函数的设计需要避免不必要的压扩，以避免产生额外的复杂度和额外的失真。故而，考虑对于幅度较小的信号，不进行压扩处理；对于幅度较大的信号，压扩函数需要有效降低PAPR，同时不产生过高的失真。故而，压扩后OFDM信号样点的幅度满足的PDF 的形状需要与原始的瑞利分布函数的形状相接近。

3.1 分段非线性压扩函数设计

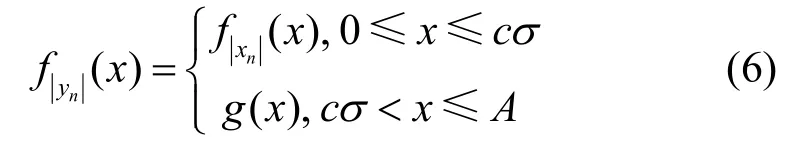
为了确保压扩后OFDM 信号样点的PSD 性能，要求压扩函数具备连续性，即压扩后OFDM信号样点幅度满足的PDF 为连续函数，即是连续函数，它需要在分段点x=cσ处连续。此时，可以得到

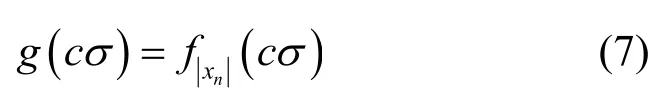
为了降低压扩失真，函数g(x)需要尽可能接近原始的瑞利分布函数。考虑将g(x)设定为三角函数，记作

其中，b是形状因子，负责控制三角函数的形状。使用三角函数是一种非常好的选择，一方面，三角函数在形状上与瑞利分布函数足够接近。这对于降低压扩失真非常有效。另一方面，三角函数的表达式十分简洁，容易推导出压扩后OFDM 信号样点的PDF 对应的最终利于推导压扩函数的表达式。由于g(x)是PDF，故而，在区间中，g(x)需要满足

此时，得出结论

进一步，为了让分段函数有意义，要求

此时，将限幅值A重新写作

故而，可以得出结论

使用该压扩算法时，压扩后OFDM 信号样点的最大理论PAPR 为

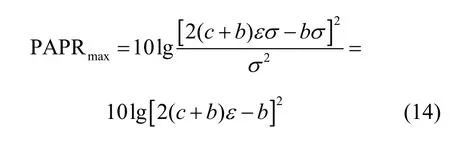
此时，可以得到设计的压扩函数在压扩后OFDM 信号样点满足的PDF 为

其中，

压扩后OFDM 信号样点的PDF 对应的CDF 为

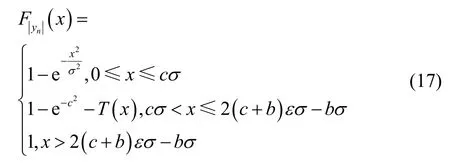
其中，

其中，

将式(19)和式(20)代入式(5)，可以得到对应的压扩函数为

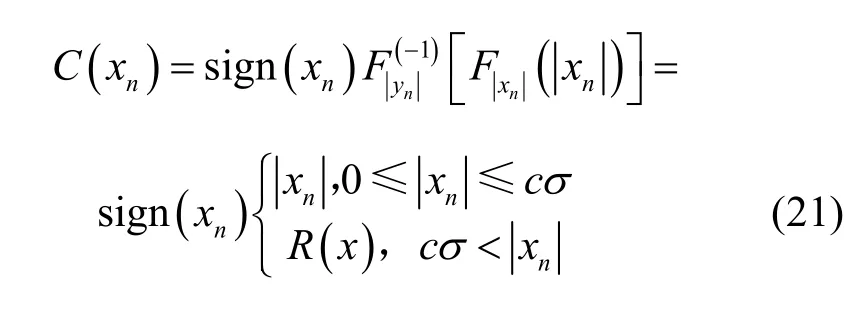
其中，

3.2 压扩函数参数推导

在压扩函数的参数中，给定任意的满足式(13)的ε，通过求解二元方程组求解对应的参数c和b。参数c和b需要满足2 个条件，一个条件是参数c和b需要满足CDF 的定义，即此时，可以得到

通过对式(23)进行化简，可以得到

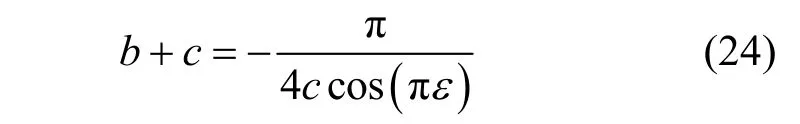
进一步，假设 cos（πε）=t，则式(24)可以被改写为

参数c和b需要满足的另一个条件为压扩后和压扩前OFDM 信号样点的平均功率相等，即

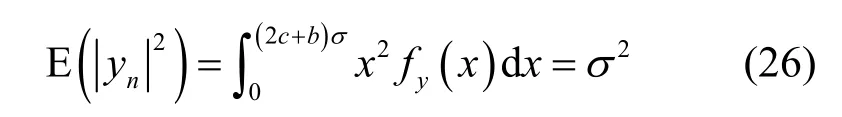
将式(25)和式(26)进行联立，可以求解出对应的压扩参数c和b。首先，将式(26)进行展开，可以得到

其中，

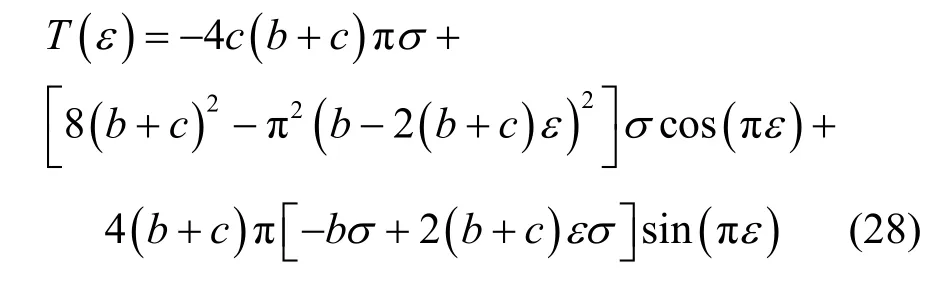
将cos(πε)=t代入式(28)中，并进行化简，可以得到

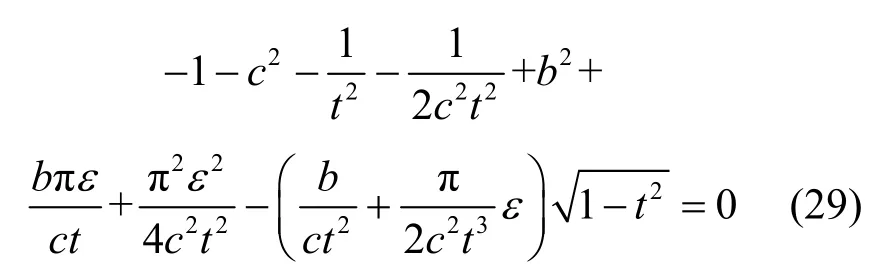
将式(25)中的b和c的关系代入式(29)中，可以得到

此时，通过化简式(30)，可以得到

通过求解式(31)中的关于c的一元二次方程，可以得到

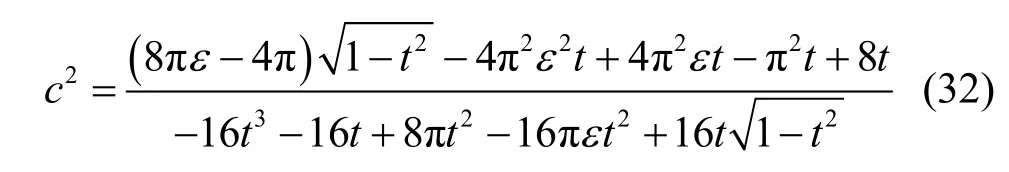
假设

此时，可以得到

图2 展示了参数ε与PAPR 的关系。通过图2可以看出，随着参数ε的增大，压扩后OFDM 信号样点的PAPR 逐渐增大。该压扩算法可以通过灵活调整参数，使压扩后OFDM 信号样点的PAPR 位于4.25～6.15 dB。

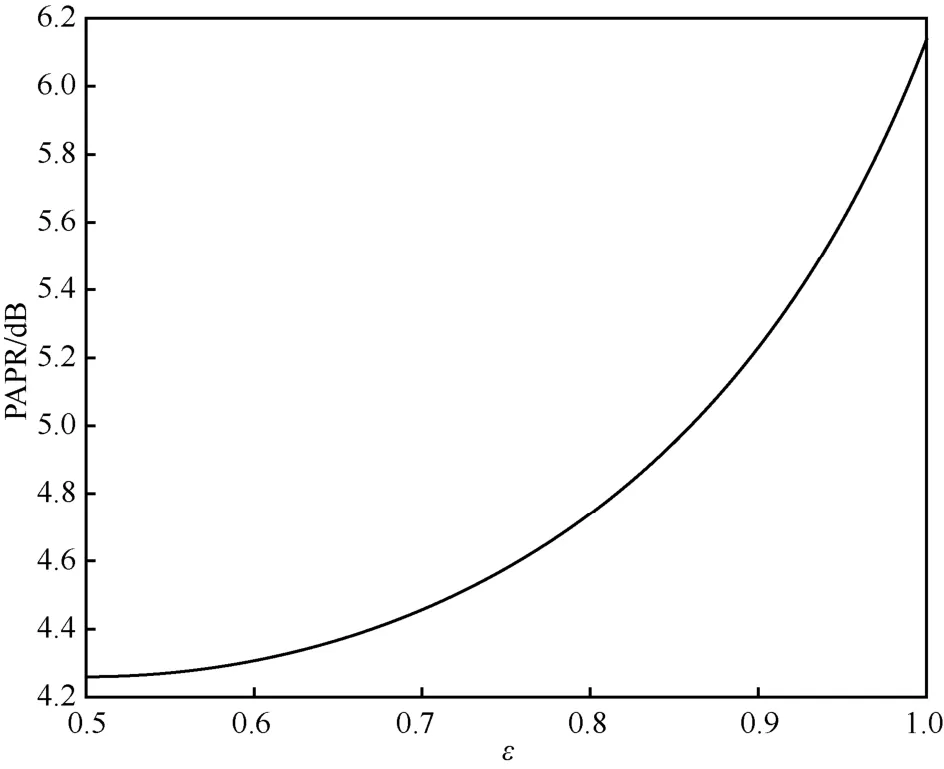
图2 参数ε 与PAPR 的关系

图3展示了不同的参数ε对应的压扩后OFDM信号样点的PDF。通过图3 可以看出，一方面，压扩后OFDM 信号样点幅度满足的PDF 在形状上与瑞利分布函数相接近。另一方面，随着参数ε的增大，压扩后OFDM 信号样点的PDF 的形状与原始的瑞利分布函数的形状越来越接近，且压扩后OFDM 信号样点的PDF 的限幅点越接近零点。

图3 不同的参数ε 对应的PDF

图4 展示了不同的参数ε和对应的压扩函数。通过图4 可以看出，当信号的幅度较小时，压扩函数的图像与不进行压扩处理的过原点的直线十分接近。随着信号幅度的增大，压扩函数的曲线缓慢增加至一个固定的值。这确保压扩后OFDM 信号样点的最大幅度不超过一个固定的值，并且确保较低的带外泄露。

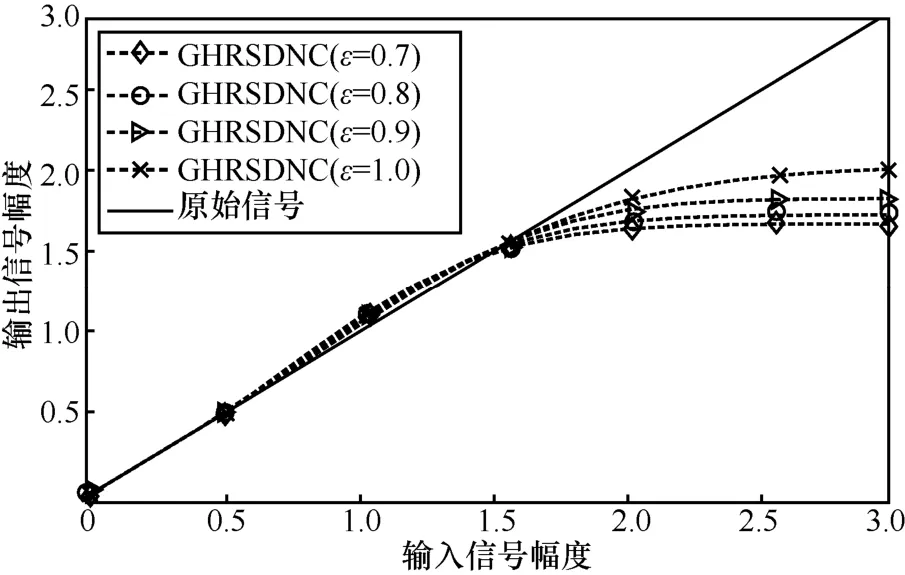
图4 不同的参数ε 对应的压扩函数

通过图2～图4 可以看出，压扩函数的参数ε对压扩函数的设计至关重要。压扩函数的参数ε控制着压扩后OFDM 信号样点幅度对应的PDF 的形状，以及压扩后OFDM 信号样点的最大幅度值。一方面，当ε的值增大时，压扩后OFDM 信号样点幅度满足的PDF 更接近原点，从而PDF 失真更少，但是，相应地，压扩后OFDM 信号样点的PAPR 也会更大；另一方面，当ε的值减小时，压扩后OFDM信号样点的PAPR 更小，但是，对应的PDF 的失真也更大。

图5 展示了不同压扩函数的对比，对比的压扩函数包括Wangs 算法[15]、ISQR 算法[16]、EC 算法[13]和ALC 算法[21]中的函数。在整体的仿真中，OFDM 信号样点的平均功率被归一化为1.0 π rad/sample。在对比的Wangs 算法中，c表示分段点的值，A表示限幅点的值；在对比的ISQR 算法中，c表示分段点的值；在对比的EC 算法中，d表示压扩后OFDM 信号样点幅度的d次幂；在对比的ALC 算法中，M表示限幅因子，s表示曲线的弯曲因子，v表示输入信号的缩放因子。

通过图5 可以看出，与EC 算法和ALC 算法中的函数相比，由于没有对幅度较小的信号进行压扩，本文压扩函数在幅度较小的部分，与原始的过原点的直线几乎重合。对于幅度较大的信号的部分，该压扩函数的图像缓慢地趋近于限幅值，这有助于提升压扩函数的PSD 性能。

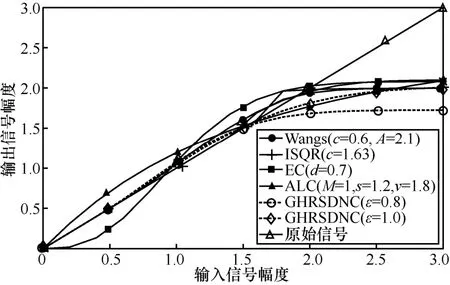
图5 不同压扩函数的对比

3.3 参数松弛方法

通过图2 可以看出，ε的值从0.5 变到1.0 时，PAPR 的变化范围为4.21～6.15 dB。为了提高压扩算法的灵活性，提升压扩后OFDM 信号样点的PAPR 的变化范围，考虑将式(26)中的压扩后和压扩前OFDM 信号样点的平均功率相等的约束改为压扩后和压扩前OFDM 信号样点的平均功率大约相等的约束，即

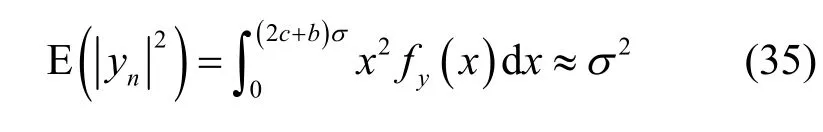
参考式(26)，可以把式(35)展开为

式(36)可被改写为

其中，

其中，

图6 展示了c和F的关系。通过图6 可以看出，随着c的增大，F的值逐渐趋近于1。且无论ε的值取多少，当c≥2 时，F的值都可以近似趋近于1。对任意的ε，除了求解出精确的c和b的值以外，当c≥2 时，都可以认为压扩函数的参数满足压扩后和压扩前OFDM 信号样点的平均功率相等。

图6 c 和F 的关系

图7 展示了当c≥2 时，参数c、ε和PAPR的关系。从图7 可以看出，当c固定时，随着ε的增大，PAPR 逐渐增大。当ε固定时，随着c的增大，PAPR 逐渐增大。因而，该参数松弛的方法进一步扩大了PAPR 的范围，提升了参数设计的灵活性。

图7 当c≥2 时，c、ε 和PAPR 的关系

3.4 压扩算法流程设计

算法1 展示了设计的压扩算法的发送端算法流程。该压扩算法可以分为两大部分。在第一部分中，基于预设的参数ε的值和OFDM 输入信号样点的平均功率σ2，求解参数c和参数b的值。在第二部分中，当输入的信号序列的幅度小于给定的值cσ时，压扩后OFDM 信号样点的幅度与压扩前相等。当输入的信号序列的幅度大于给定的值cσ时，将使用压扩函数对输入信号序列进行处理。通过算法1 可以看出，在发送端，压扩算法需要存储预设的ε的值、总的子载波数目N和发送信号的平均功率σ2。

算法1GHRSDNC 压扩算法流程

输入预设ε的值、OFDM 的子载波数目N、OFDM 的原始的发送信号序列x[i]和原始的OFDM信号样点的平均功率σ2

输出压扩后的OFDM 信号样点序列yn

1) 预设主要参数：根据式(24)和式(26)求解参数c和b的值

4 仿真分析

为了验证本文压扩算法在PAPR、BER、PSD等方面的性能，本节对设计的压扩算法进行相应的仿真分析。在仿真时，选取OFDM 系统的子载波数目为256，采用4 倍过采样，并选取总的OFDM 的符号数为100。在整体仿真时，OFDM信号样点的平均功率被归一化为1.0 π rad/sample。本文压扩算法与EC 算法[13]、ISQR 算法[16]、Wangs算法[15]和ALC 算法[21]进行比较。在BER 性能的仿真中，还将验证OFDM 信号样点在经过了固态功率放大器（SSPA,solid state power amplifier）以后的BER 性能。压扩后OFDM 的信号样点在经过SSPA 后的模型为

其中，Asat为功率放大器的饱和因子，在本次仿真中，Asat=1.5；p为控制功率放大器的形状的因子，在本次仿真中，p=2.0。

图8 展示了不同压扩算法的PAPR 的互补累积分布函数（CCDF,complementary cumulative distribution function）。从图8 可以看出，设计的压扩函数的PAPR 的CCDF 曲线下坠迅速。特别地，在CCDF=1.0×10−4时，设计的压扩算法在ε=0.6 时，对应的PAPR 大约为4.5 dB；在ε=0.8时，对应的PAPR 大约为5.0 dB；在ε=1.0 时，对应的PAPR 大约为6.3 dB。

图8 不同压扩算法的PAPR 的CCDF

图9 展示了不同压扩算法的BER 性能。从图9可以看出，当BER=1.0×10−4时，GHRSDNC 算法在ε=0.6 时，需要的最低的Eb/N0大约为9.3 dB，比EC 算法低0.2 dB，比ALC 算法低0.7 dB。当BER=1.0×10−4时，GHRSDNC 算法在ε=0.8 时，需要的最低的Eb/N0大约为9.0 dB，比EC 算法大约低0.5 dB，比ALC 算法大约低1.0 dB。

图9 不同压扩算法的BER 性能

图10 展示了不同压扩算法在经过了SSPA 以后的BER 性能。通过图10 可以看出，当BER=1.0×10−4时，GHRSDNC 算法在ε=0.6 时，对应的最低的Eb/N0为10.8 dB，比ALC 算法低0.2 dB。

图10 不同压扩算法经过SSPA 后的BER 性能

图11 展示了不同压扩算法的PSD 性能。通过图11 可以看出，本文设计的压扩算法在PSD 的性能方面具备优势。当归一化功率为1.0 π rad/sample时，GHRSDNC 算法在ε=0.6 时的带外泄露功率为−27.0 dB，比ALC 算法低2.0 dB。当归一化功率为2.0 π rad/sample 时，GHRSDNC 算法在ε=0.6 时的带外泄露功率为−39.9 dB，比ISQR 算法低5.0 dB。

图11 不同压扩算法的PSD 性能

表1 展示了不同压扩算法的性能比较。其中PSD 性能表示当归一化频率为2.0 π rad/sample 时，对应的带外泄露功率。通过表1 可以看出，当PAPR相同时，本文压扩算法在BER 性能、PAPR 性能和PSD 性能方面存在优势。例如，当设计的GHRSDNC算法在ε=0.6 时，与EC 算法在CCDF=1.0×10−4时，对应的PAPR 都为4.5 dB，但GHRSDNC 算法在ε=0.6、BER=1.0×10−4时，对应的Eb/N0比EC 算法低0.2 dB；在归一化频率为2.0 π rad/sample 时，GHRSDNC 算法在ε=0.6 时，对应的带外泄露功率比EC 算法低0.1 dB。

表1 不同压扩算法的性能比较

5 结束语

本文设计了一种基于瑞利分布和三角函数分布相结合的非线性压扩算法抑制OFDM 系统的PAPR。在该算法中，不对幅度较小的信号进行压扩处理，对于幅度较大的信号，将压扩后OFDM信号样点的PDF 从瑞利分布改为三角函数分布。根据概率守恒和功率守恒，可以推导出压扩函数的参数的理论表达式。仿真结果表明，本文设计的算法可以在有效降低OFDM 信号样点的PAPR的基础上，确保较低的误码率和良好的PSD 性能。例如，GHRSDNC 算法在ε=0.8、CCDF=1.0×10−4时，对应的 PAPR 为 5.0 dB，此时，它在BER=1.0×10−4时，不经过功率放大器，对应的最低的Eb/N0大约为9.0 dB。并且，当归一化频率为1.0 π rad/sample 时，GHRSDNC 算法对应的PSD的带外泄露功率为−28.0 dB。