基于Bartlett 和多分类F 检验侧信道泄露评估

王娅茹，唐明

（1.武汉大学国家网络安全学院，湖北 武汉 430072；2.武汉大学空天信息安全与可信计算教育部重点实验室，湖北 武汉 430072）

1 引言

自Kocher 等[1]指出可以通过侧信道能量分析揭示智能卡中的秘密信息以来，侧信道攻击（SCA,side channel attack）成为加密实现和设备安全的重要威胁之一。多年来，研究者专注于各种侧信道攻击方法和对应防护策略的研究[1-5]，以保护密码实现免受此类攻击。随着防护策略集成到密码实现中，评估密码实现对SCA 的抵抗能力成为一个必须思考的问题。泄露检测是针对此问题的一种简单、有效的解决方法。泄露检测通过对黑盒模型下侧信道功耗样本是否包含泄露信息进行检测，初步评估密码实现的安全性。泄露检测原理是通过对功耗样本的统计分析，检验不同明文对应的功耗样本分布是否可区分。如果可以区分，则认为功耗样本包含秘密信息，即存在侧信道泄露；否则认为不存在侧信道泄露。

2011—2013 年，Goodwill 等[6-7]给出了测试向量泄露评估（TVLA,test vector leakage assessment）技术进行侧信道泄露检测。在TVLA 技术中，首次将统计学中的Welch’s t 检验[8]用于泄露检测，以评估不同明文对应的功耗样本分布是否可区分。TVLA 技术提出后，侧信道方向的研究者们利用该方法，进行各种加密设备和实现的泄露检测和安全评估策略的相关研究[9-11]；为进一步提高侧信道安全评估效率，研究者开始对消除泄露检测中环境噪声影响的方法[12]和优化侧信道泄露检测流程[13-16]产生兴趣。随着研究的深入，泄露检测成为侧信道研究中一个重要方面。t 检验仍是目前泄露检测中最常用的检测方法[17-18]，它将明文分成两类：固定明文集和随机明文集。通过比较固定明文（和密钥）集与随机明文（和密钥）集在相同加密实现下，产生的功耗样本分布是否可区分，来判别是否存在侧信道泄露。一般认为如果功耗样本不可区分，即固定明文集和随机明文对应的功耗样本分布相同，则无侧信道泄露。该方法利用t 检验评估待测设备特定采集的两组功耗曲线均值的差异性，从而判断是否有信息泄露并给出密码实现安全性的初步评估。文献[2,19-20]仔细讨论的t 检验的主要优势在于：通过比较两类（固定明文集与随机明文集）功耗样本均值，可以将泄露检测问题简化为简单的统计估计。t 检验具有简单、高效的优点且只利用较少的算法实现知识，但是有2 个缺点[21]：1) 该方法把评估曲线分为两组，而不是按照目标中间值的实际大小来分组，分类有限，可能会导致实际评估时出现假阴性；2) 检测样本的评估结果比较依赖统计距离。t 检验仅考虑固定明文集和随机明文集对应的功耗样本的均值是否区分，而功耗样本的不可区分性不仅要求均值不可区分还要求方差不可区分。本文发现当固定明文集和随机明文集对应的功耗样本分布均值差异越小，P值越大；当样本均值差异小于0.01时，t 检验的P值大于阈值，t 检验会有漏检的风险。

基于上述问题，本文提出在泄露检测之前，对样本的均值、方差等参数差异情况进行评估，并根据参数差异度选择特定的统计学假设检验方法而不是按照TVLA 技术对所有样本均采用t 检验进行检测，完全不考虑样本分布参数的差异性。进而提出用Bartlett 检验代替t 检验对均值差异小于方差差异的功耗样本进行检测，以解决t 检验可能出现的漏检。此外，Bartlett 检验将功耗样本按明文汉明权重（HW,Hamming weight）分成多类，可以解决分类有限的问题。对于均值差异大于方差差异的功耗样本，虽然依然可以使用t 检验进行泄露检测，但基于t 检验分类有限的问题，本文提出用多分类F 检验代替t 检验，进而提出基于Bartlett 和多分类F 检验侧信道泄露评估（Bartlett-F 检验）方法，旨在解决传统TVLA 技术中存在的问题。当接受假设H0的概率（P值）小于阈值1.0 ×10-5，则功耗样本有泄露。实验结果表明，对于均值差异（小于0.01）小于方差差异（大于0.5）的样本，Bartlett 检验的P值小于阈值1.0 ×10-5所需样本量为1.5 ×104。而对t 检验而言，样本量达到3.0 ×104时，P值大于阈值。为使t 检验的P值小于阈值，则需要更大的样本量。因此，在相同样本量下，与Bartlett 检验相比，t 检验存在漏检。对于方差差异（小于0.3）小于均值差异（小于1.0）的样本，P值小于阈值的样本量为2.0 ×102，而F 检验扩大了样本分类，P值小于阈值的样本量仅为 t 检验的因此，本文的Bartlett-F 检验可以解决传统TVLA 技术在泄露检测中存在的问题。

本文的主要工作如下。

1) 本文发现利用t 检验进行泄露检测，当样本量相同时，均值差异越小，P值越大；当两组样本均值差异小于0.01时，t 检验的P值大于阈值，存在漏检风险。

2) 基于1)发现，本文提出在泄露检测前，添加对样本分布参数（均值和方差）的差异度评估。

3) 根据2)中的评估结果，本文提出采用Bartlett检验代替t 检验解决1) 的问题，并通过比较实验验证Bartlett 检验的有效性。

4) 基于t 检验分类有限可能导致的假阴性，本文提出用多分类F 检验代替t 检验对均值差异大于方差差异的功耗样本进行泄露检测，以降低t 检验因分类有限导致的假阴性。

2 Welch’s t 检验

TVLA 技术利用统计学中的Welch’s t 检验[17-22]来评估加密实现抵抗侧信道攻击的能力。t 检验对随机明文集和固定明文集对应功耗样本的均值差异进行评估，以判定加密实现或设备是否存在信息泄露。t 检验的具体内容如下。

0L和L1分别表示固定明文集和随机明文集对应的侧信道功耗样本，L0和L1的样本量、样本均值和样本方差分别为。假设H0为固定明文集和随机明文集对应的功耗样本均值不存在差异。检验统计量t和自由度v的计算式分别为

概率密度函数及接受假设H0的概率P分别为

其中，Γ(·) 是gamma 函数。

t 检验通常设定4.5[23-24]为判定接受或拒绝假设H0的阈值，将t 检验的统计量与阈值4.5 进行比较。如果，则拒绝假设H0。这是因为当v＞1000，P=2tcdf(4.5,v) ＜ 1.0 ×10-5[20]时，这意味着以小于0.000 01 的概率接受假设H0，即以大于0.999 99 的概率拒绝假设H0。本文将1.0 ×10-5作为阈值，若概率P＜ 1.0 ×10-5，则拒绝假设H0，表明加密实现或设备有侧信道泄露。

本文根据明文汉明权重对功耗样本进行分类，针对不同的输入类I i∈I进行加密操作，其中I是所有可能的输入集合，采集不同输入类Ii对应的功耗泄露记为Li(1≤i≤m)，样本分类数为m，所有功耗样本集合为L，总样本量为N，每类功耗样本的样本均值为xi、样本方差为均值为μi、方差为其中均未知。

3 关键技术

3.1 问题描述

t 检验一般用于检测两类样本的均值是否存在差异。本文发现在侧信道泄露检测中，检测结果与固定明文集和随机明文集对应功耗样本的均值差异相关。当均值差异较大时，t 检验检测效果较好；当两样本均值相同、方差不同时，统计学判定两样本服从不同分布，而t 检验结果显示两样本服从相同分布。因此，利用t 检验对均值近似相同、方差不同的样本进行泄露检测时，存在漏检（加密算法或设备事实上存在泄露的，t 检验未发现泄露）风险。

利用t 检验分别对该样本进行泄露检测，检测结果如图1(b)所示。由图1(b)可知，当样本量相同时，均值绝对值差越小，P值越大；当样本均值差的绝对值小于0.01 时，t 检验的P值大于阈值，存在漏检风险。为避免出现此种漏检，本文提出在泄露检测前对样本参数差异进行评估。

图1 不同均值差下执行t 检验

3.2 样本参数差异评估

本文以每类样本参数差异的绝对值来评估样本参数差异。在t 检验中，固定明文集和随机明文集对应的功耗样本分别为L0和L1，L0和L1的样本量、样本均值和方差分别为。当将功耗L样本分成m类样本集Li(1≤i≤m)时，Li(1≤i≤m)的样本量、样本均值和样本方差为

3.3 Bartlett-F 检验

本节提出了基于Bartlett 和多分类F 检验侧信道泄露检测。Bartlett -F 检验流程如图2 所示。

图2 Bartlett -F 检验流程

Bartlett -F 检验过程如下。

1) 将明文Mi按汉明权重分成m类，对应功耗曲线记为Li。假设每类检测样本集的样本量均为n（n可以根据实验需要进行调整）。

2) 从分类中随机选择j(1≤j≤m)类功耗样本Li，计算Li的样本均值和样本方差记为

3) 对|d1-d2|进行评估，如果|d1-d2|趋于d2，即d1趋于0，则样本间方差差异大于均值差异；如果|d1-d2|趋于d1，则均值差异大于方差差异。

4) 如果样本间均值差异小于方差差异，则使用Bartlett 检验代替t 检验；如果样本间均值差异大于方差差异，使用多分类F 检验代替t 检验。

3.3.1 Bartlett 检验

如果|d1-d2|趋于d2，即d1趋于0，则两样本均值近似相等，样本间均值差异小于方差差异。利用Bartlett 检验对样本的方差是否可区分进行检验。假设H0为各样本类的方差相同，则统计量2X和自由度v计算式分别为

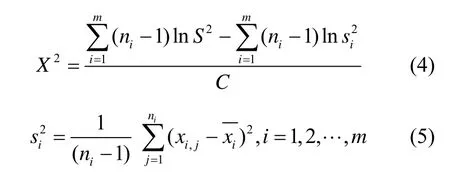
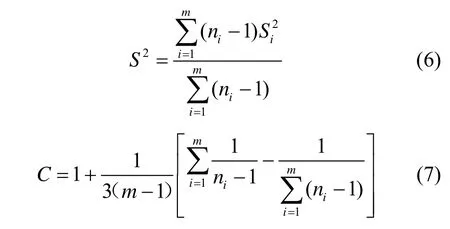
由于自由度为v=m-1，接受假设H0的概率表示自由度，Γ(·) 表示gamma 函数。统计量X2越大，P0越小，则以较大概率拒绝H0。

3.3.2 多分类F 检验

如果|d1-d2|趋于d1，即d2趋于0，则两样本方差近似相等，样本间方差差异小于均值差异。通过多分类F 检验代替t 检验对样本的均值是否可区分进行检验。根据明文汉明权重将采集到的功耗分成m类，记为Li(1≤i≤m)，其中每个分类的样本量为ni。假设H0为各样本类的均值相同，则统计量F为

其中，为总样本均值，N为总样本量，n i为第i类样本的样本量，为第i类样本均值，m为分类数，则接受假设H0的概率

其中，v1=m-1、v2=N-m表示自由度。接受假设H0的概率P0越小，拒绝H0的证据越充分。

此外，设检测有泄露概率均为P，t 检验仅将功耗样本分为两类，对两类样本均值进行比较，整个检测过程只进行一次比较判定。因此，假阴性的概率为P。而Bartlett 检验和多分类F 检验将按明文汉明权重（也可以按照其他分类标准分类，如汉明距离），将功耗样本按明文汉明权重分成m类，比较各类对应的功耗样本的均值或方差是否相同，需要进行m-1次判定，假阴性概率为Pm-1。与t 检验相比，假阴性概率为t 检验的1%。因此，扩大分类可以降低t 检验由于分类有限导致的假阴性。

3.4 推广到多变量

随着高阶掩码应用到软件实现和硬件设计中，每个共享因子泄露产生的时刻不同。所以进行泄露检测时，不能再通过对单个时刻的功耗进行检验来确定是否有泄露，需要利用覆盖所有共享因子泄露时刻的组合功耗来确定是否有泄露。常用的方案是利用组合函数对所有泄露时刻的功耗进行预处理，以获取组合功耗，然后再对其进行泄露检测。文献[25]已证明是汉明权重模型下最优的组合函数，其中表示ti时刻的功耗，表示该时刻的功耗样本均值，d表示共享因子的数量。本文用此函数对功耗样本进预处理。

4 实验及结果分析

4.1 仿真

由图3(b)可知，当样本量为0.5 ×104时，Bartlett检验接受假设H0概率P小于阈值，且样本量为2.0 ×104时，P值为1.0 ×10-16，远小于阈值。而对t检验而言，当样本量大于5.0 ×104时，概率P小于阈值。由于|d1-d2|趋于d2，即d1趋于0，则两样本均值近似相等，样本间均值差异小于方差差异。因此，在相同样本量下，与Bartlett 检验相比，用t检验对均值差异小于方差差异的功耗样本进行泄露检测，会存在漏检风险。

图3 对均值差异小于方差差异的样本执行Bartlett 检验和t 检验

由图4(a)可知，样本均值差异接近1，方差差异小于0.3。根据3.2 节差异度大小的描述可知，如果|d1-d2|趋近d1，则该样本均值差异大于均方差差异。利用多样本F 检验和t 检验分别对该样本进行泄露检测，检测结果如图4(b)所示。

由图4(b)可知，t 检验的P值小于阈值所需的样本量2.0 ×102，而多样本F 检验所需的样本量是t 检验的1 10。因此，与t 检验相比，扩大分类的F检能降低因t 检验分类有限导致的假阴性。

图4 对均值差异大于方差差异的样本执行F 检验和t 检验

泄露检测时，检测结果与信噪比、样本分类等因素密切相关。在检测时应该考虑这些因素的影响。为了便于控制影响因素的大小，本文利用仿真功耗采样来研究信噪比、样本分类等对检测结果的影响。

为研究扩大样本分类对检测结果的影响，分别将样本分为四类、五类和六类，利用Bartlett 检验对分类数m=4、利m=5和m=6的情况进行检测，检测结果如图5 所示。

图5 对分类数不同的样本执行Bartlett 检验

由图5 可知，当m=6时，Bartlett 检验的P值小于阈值的样本量2.5 ×103；当m=4和m=5时，P值小于阈值所需样本量分别为8.5 ×103和4.0 ×103。实验结果表明，随着样本分类的增加，Bartlett 检验的P值小于阈值所需的样本量降低。

本文利用 Bartlett 检验分别对不同信噪比SNR=0.1 dB、SNR=1.0 dB 和SNR=10.0dB 环境下的功耗样本进行检测，检测结果如图6 所示。

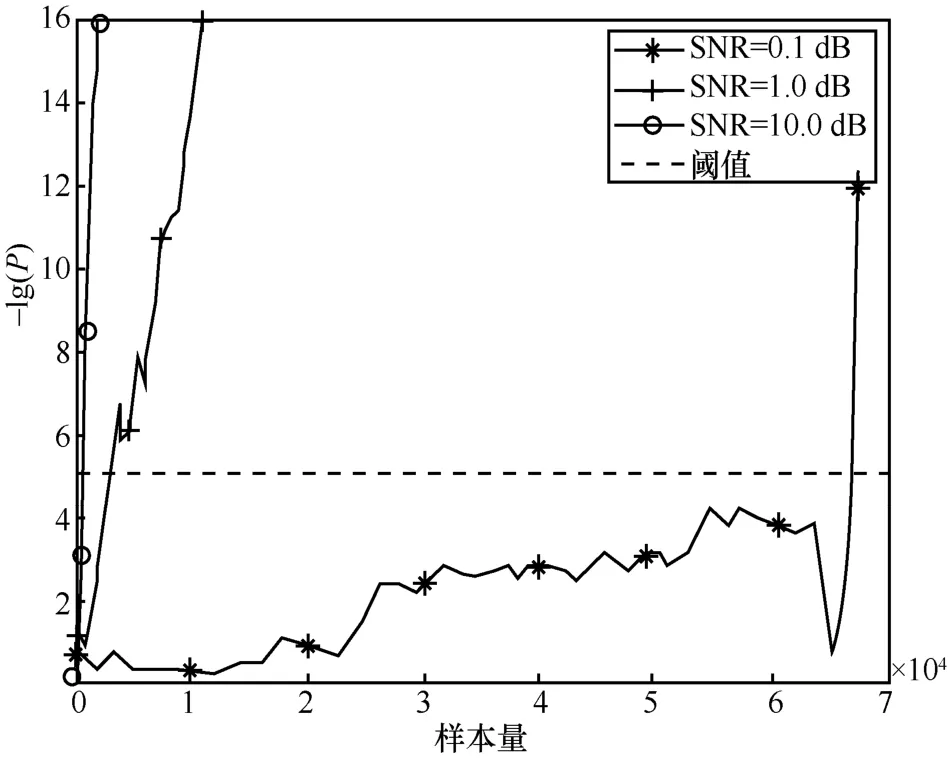
图6 对不同信噪比环境下的样本执行Bartlett 检验

由图6 可知，当信噪比SNR=0.1 dB 时，P值小于阈值所需的检测样本量为时，所需的样本量为时，所需的样本量仅为实验结果表明，在Bartlett 检验中，SNR=1.0 dB 时，P值小于阈值所需的样本量大约为SNR=10.0 dB 时的34 倍。因此，SNR 的减小降低Bartlett 检验优势。

4.2 实验

本文还利用公开数据集技术 DPA Contest-V4[26]，按照Bartlett-F 检验和TVLA 技术的泄露检测过程进行实验。实验前，首先对数据进行预处理；在实验中，利用峰值提取技术和CPA 技术，提取出泄露产生时刻。由于DPA Contest-V4 数据集是AES 在RSM 掩码实现下的功耗采集，泄露不在同一时刻发生。因此，在实验中选取作为预处理函数，对功耗样本进行预处理。相关系数与采样时刻如图7 所示。

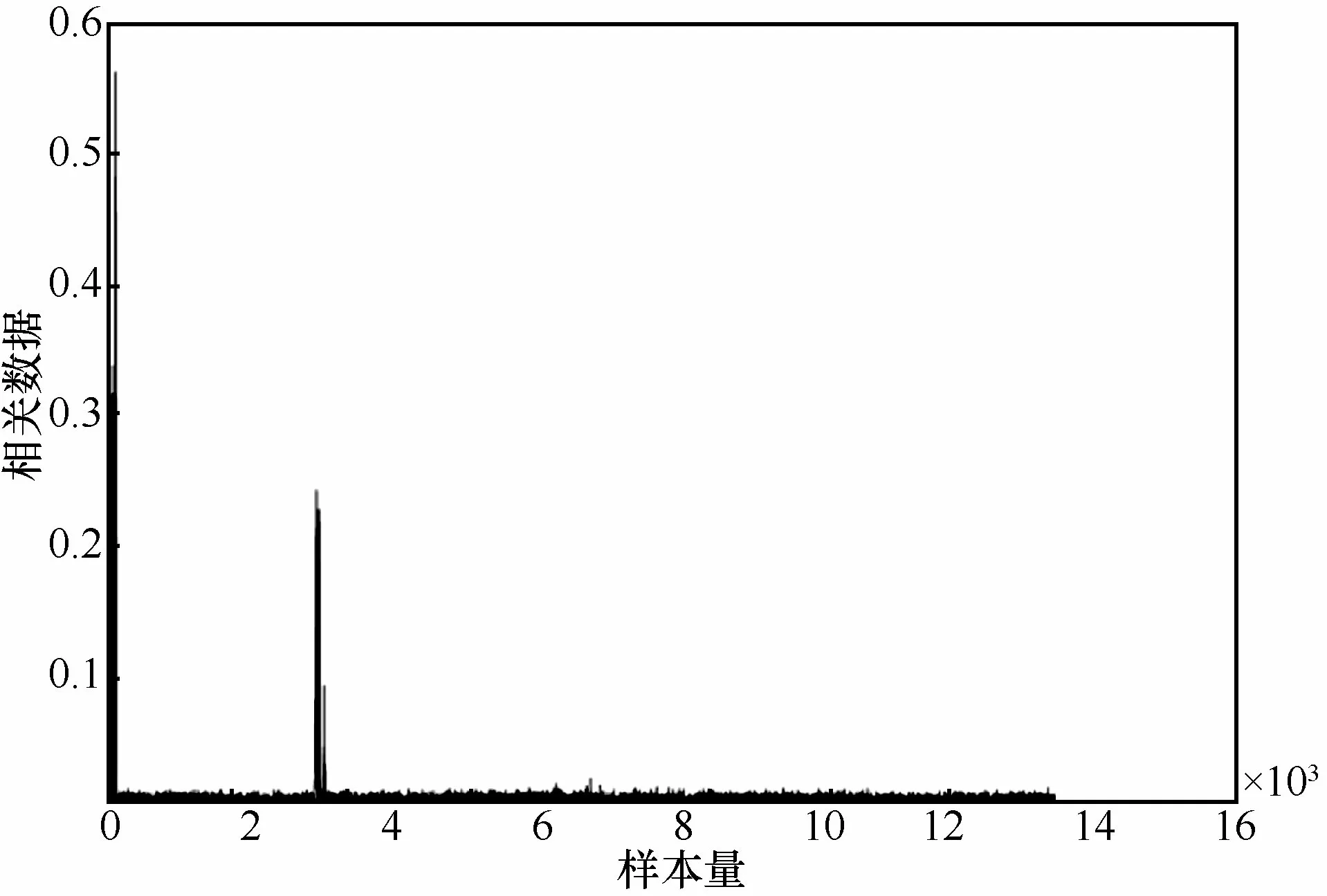
图7 相关系数与采样时刻

随后对预处理后的功耗样本进行均值差异和方差差异评估，如图8(b)所示。由图8(a)可知，样本绝对值差趋于0 且样本均值差异小于方差差异。利用Bartlett 检验和t 检验分别进行泄露检测，检测结果如图8(b)所示。

由图8(b)可知，Bartlett 检验的P值小于阈值所需的样本量1.5 ×104；当样本量达到3.0 ×104，P值小于阈值1.0 ×10-5，而对t 检验而言，样本量达到3.0 ×104时，P值大于阈值。为使t 检验的P值小于阈值，则需要更大的样本量。因此在相同样本量下，与Bartlett 检验相比，t 检验存在漏检。

图8 执行Bartlett 检验和t 检验

5 结束语

传统TVLA 技术通过比较固定明文集和随机明文集对应的功耗样本的均值是否存在差异，来判定样本是否服从相同分布，以说明加密实现是否存在泄露。而事实上，样本服从相同分布，不仅要求样本均值而且要求样本方差均相同。本文发现，当固定明文集和随机明文集对应的功耗样本量相同时，均值差异越小，P值越大；且均值差异小于0.01 时，t 检验的P值大于阈值，t 检验会有漏检的风险。另外，t 检验将功耗分为两组，而不是按照中间值的大小来分组，样本分类有限，可能会导致评估时出现假阴性。基于上述问题，本文提出在泄露检测前，对样本的均值和方差等参数差异进行评估，并根据参数差异选择检验方法，提出将Bartlett 检验代替t 检验用于各样本类的均值差异小于方差差异的功耗样本的泄露检测，以解决t 检验在检测中存在的漏检风险，同时Bartlett 检验将功耗样本按明文汉明权重分成多类，可以解决分类有限的问题。此外，对均值差异大于方差差异的功耗样本，本文建议用多分类F 检验代替t 检验，扩大样本分类，提出Bartlett F 检验来解决传统TVLA 技术中存在的问题。实验结果表明，Bartlett 检验的P值小于阈值的样本量，仅为1.5 ×104。当样本量达到3.0 ×104时，P值小于阈值1.0 ×10-5。而对t 检验而言，当样本量达到3.0 ×104时，P值大于阈值。在相同样本量下，Bartlett 检验可以解决t 检验出现的漏检。对于方差差异小于均值差异的样本，t 检验的P值小于阈值所需的样本量，为2.0 ×102，而多样本F 检验所需的样本量是t 检验的1 10。当样本量为2.0 ×102时，多样本F 检验的P值大于1.0 ×10-16而t 检验的P值仅为1.0 ×10-5，多样本F 检验可以降低t 检验假阴性概率。因此，在侧信道泄露检测时，本文提出的 Bartlett-F 检验可以有效解决TVLA 技术存在的问题。