MIMO-OFDM 系统的信道与脉冲噪声联合估计方法

吕新荣，李有明，国强

（1.宁波大学科学技术学院，浙江 宁波 315300；2.宁波大学信息科学与工程学院，浙江 宁波 315211；3.哈尔滨工程大学信息与通信工程学院，黑龙江 哈尔滨 150001）

1 引言

现代通信系统已经将正交频分复用（OFDM，orthogonal frequency division multiplexing）和多输入多输出（MIMO，multiple input multiple output）作为物理层核心技术。MIMO-OFDM 能有效利用OFDM 对抗频率选择性衰落，同时利用MIMO 提高系统容量[1]。

安全高速的通信系统是现代社会各行业智能化建设的基础。在智能交通[2]、智能电网[3]、智慧海洋[4]、智能工厂[5]等领域，许多生产活动会产生大量脉冲噪声。脉冲噪声具有非高斯、突发性、持续时间短、能量高等特点。脉冲噪声的时域特性导致它在频域上会影响OFDM 的所有子载波，使所有子载波的信噪比急剧降低，从而导致OFDM 系统性能的急剧下降[6]。

传统消除脉冲噪声的方法是在接收端前置一个非线性的预处理器，该处理器通过设置一个阈值来判断是否存在脉冲噪声。如果存在，则利用削幅法、置零法等方法去除脉冲噪声[7]。这类方法难以获得最优阈值，导致无法有效地从接收信号中消除脉冲噪声，对有用信号造成破坏。依据脉冲噪声在时域上具有稀疏性的特性，近些年利用压缩感知技术消除脉冲噪声的方法得到了广泛关注[2,4,8]。这类方法的性能主要依赖于空子载波的数目，但空子载波数目的增多将降低OFDM 系统的频谱使用效率。对于OFDM 系统接收机而言，消除脉冲噪声是为了尽量避免脉冲噪声影响后续的信道估计和符号检测。为了在消除脉冲噪声的同时提升信道估计和符号检测的性能，一些联合估计信道、脉冲噪声和数据符号的方案陆续被提出[9-10]，这些方法主要针对单输入单输出（SISO，single input single output）OFDM系统。

随着MIMO-OFDM 系统的广泛应用，如何消除脉冲噪声对通信系统的影响逐渐引起人们关注。文献[11]利用MIMO 系统中各个接收天线上脉冲噪声之间的空间相关性，提出一种基于结构压缩感知技术的脉冲噪声抑制方法，该方法利用空子载波上的接收信号重构时域脉冲噪声。文献[12]针对MIMO-OFDM 电力线通信系统中的脉冲噪声提出了一种基于全部子载波的脉冲噪声消除方案，该方案假设接收端已经获得准确的信道状态信息，这种假设在实际系统中很难满足。借鉴SISO-OFDM 系统的信道与脉冲噪声联合估计思路，文献[13]提出了一种针对MIMO-OFDM 电力线通信系统的信道和脉冲噪声联合估计方法，该方法利用电力线信道和脉冲噪声的稀疏性，通过导频上的接收信号来重构信道和脉冲噪声，但估计性能受到导频数量的限制。

针对MIMO-OFDM 系统中的脉冲噪声消除问题，本文提出了一种基于全部子载波的信道与脉冲噪声联合估计方法。该方法利用MIMO-OFDM 系统中信道和脉冲噪声的稀疏性，将信道和脉冲噪声估计问题转换为多测量向量（MMV，multiple measurement vector）压缩感知问题，然后引入多响应稀疏贝叶斯学习（MSBL，multiple response sparse Bayesian learning）[14]理论联合估计信道和脉冲噪声。为了利用数据子载波信息来提高信道和脉冲噪声估计性能，该方法将发射数据符号视作未知参数，利用期望值最大化（EM,expectation maximization）算法进行数据符号估计，构建了一种基于全部子载波信息的压缩感知模型，实现了信道、脉冲噪声和数据符号联合估计，从而克服了现有MIMO-OFDM 系统脉冲噪声估计方法只能利用空子载波和导频子载波的缺点。仿真结果表明，与独立考虑信道、脉冲噪声和数据检测的方法相比，本文提出的方法能使MIMO-OFDM 系统获得更好的信道估计性能与误比特率性能。

2 系统模型

设MIMO-OFDM 系统的发射天线数为Nt，接收天线数为Nr，OFDM 子载波数目为N，系统框架如图1 所示。OFDM 子载波分为三部分，用于发射导频符号的子载波数目为P，空置的子载波数目为U，其余子载波用于发射数据符号。在发射端，二进制数据流经过调制后分为并行的Nt个频域OFDM 符号数据流。第p根发射天线上的频域OFDM 符号经过OFDM 调制生成时域OFDM 信号后送入发射天线。第p（1 ≤p≤Nt）根发射天线与第q（1 ≤q≤Nr）根接收天线之间的信道冲激响应（CIR，channel impulse response）向量表示为代表信道时延扩展长度。本文假设采用插入循环前缀的方式来对抗多径信道造成的频率选择性衰落。在脉冲噪声出现的场合，接收信号中除了含有可以被近似为加性白高斯噪声（AWGN，additive white Gaussian noise）的背景噪声外，还含有脉冲噪声成分。第q根接收天线接收到的时域OFDM 信号可以表示为

图1 MIMO-OFDM 系统框架

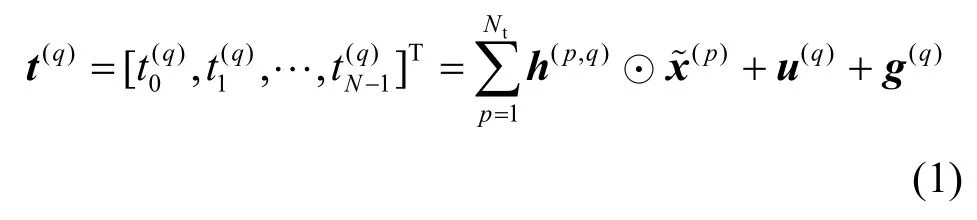
其中，符号⊙表示循环卷积，u(q)和g(q)分别表示时域脉冲噪声向量和时域AWGN 向量。接收的时域OFDM 信号经过去除循环前缀和OFDM 解调后，第q条接收天线接收的频域OFDM符号可以表示为

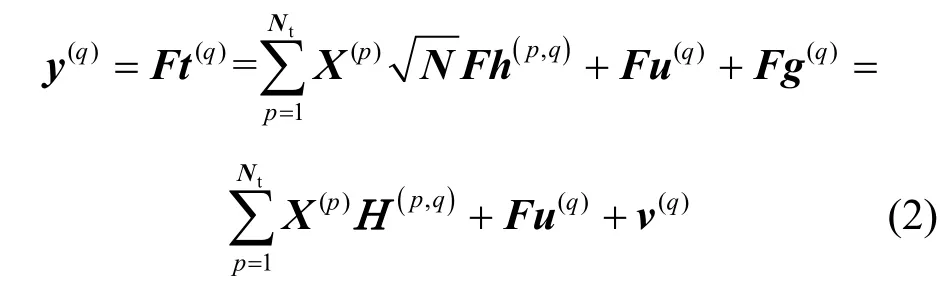
其中，X(p)=diag(x(p))表示一个N×N对角矩阵，其主对角元素由第p根发射天线的频域OFDM符号x(p)组成；F表示归一化后的N×N离散傅里叶变换（DFT，discrete Fourier transform）矩阵；表示第p根发射天线与第q根接收天线之间的信道频率响应（CFR，channel frequency response）向量；FL表示由F的前L列构成的子矩阵；由于F是一个酉矩阵，因此v(q)=Fg(q)仍是一个AWGN 向量。

考虑MIMO-OFDM 系统的每个子载波之间独立进行符号检测，则第k个子载波上基于最大似然估计的符号检测算法可表示为

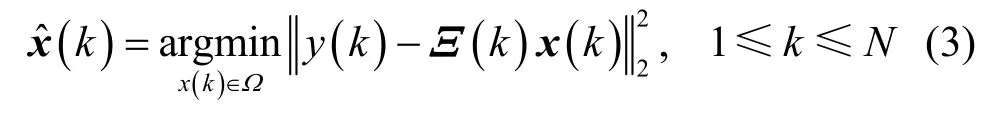
其中，Ω表示调制信号星座点集合，表示所有接收天线第k个子载波上的数据符号组成的向量，表示所有发射天线第k个子载波上的数据符号组成的向量表示接收天线与发射天线之间第k个子载波上的CFR 矩阵，具体如下

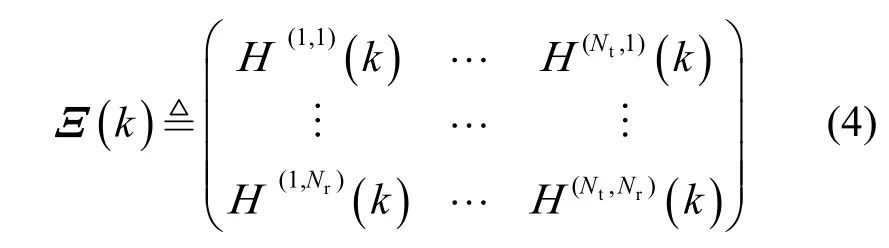
针对式(3)本文采用球形译码（SD，sphere decoding）算法进行求解。球形译码器的性能主要受限于信道状态信息的准确性和背景噪声功率的大小。脉冲噪声会极大降低现有信道估计方法的性能。此外，由式(2)可知，如果脉冲噪声不能有效去除，经过FFT 解调后脉冲噪声能量会扩展到每个子载波，这样等同于大大增加了每个子载波的背景噪声功率，进而导致SD 算法的性能急剧下降。下面介绍本文提出的信道和脉冲噪声联合估计方法。

3 基于MSBL 的信道与脉冲噪声联合估计

本文引入MSBL 来联合估计MIMO-OFDM系统信道与脉冲噪声，下面先简要介绍 MSBL理论[14]。

3.1 MSBL 理论

MSBL 理论用于解决MMV 压缩感知问题。MMV 压缩感知问题可以用如下模型表示

MSBL 可以看作稀疏贝叶斯学习理论在MMV模型上的推广，它假设矩阵X列向量X(i)的先验分布服从相同的高斯独立分布，即p(X(i);Γ)～，则矩阵X的分布可以表示为式(5)所示模型的似然函数为

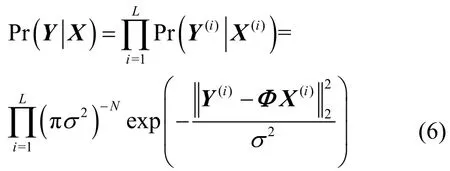
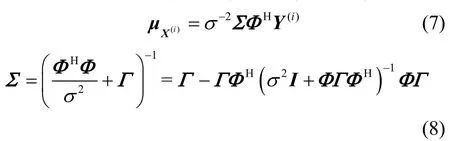
其中，ΦH是矩阵Φ的共轭转置。得到上述后验分布后，MSBL 将后验分布的均值作为矩阵X的列向量X(i)的最大后验概率（MAP，maximum a posterior）估计值。由于式(7)和式(8)中存在未知的超参数Г和σ2，为了估计这些超参数，MSBL 采用期望值最大化（EM，expectation maximization）算法进行求解。

3.2 信道与脉冲噪声联合估计

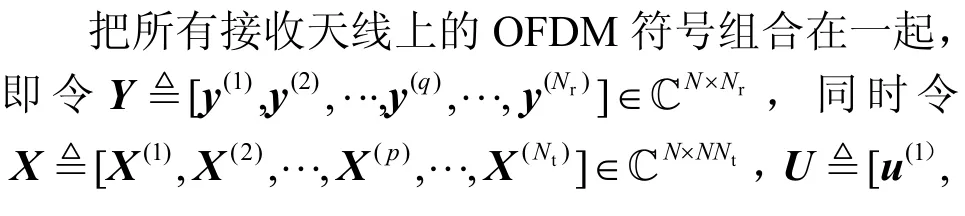
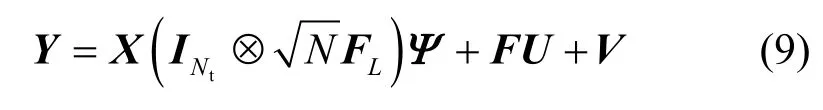
其中，表示Nt×Nt的单位矩阵，符号⊗表示Kronecker 积，表示MIMO-OFDM 系统的CIR 矩阵，如式(10)所示。

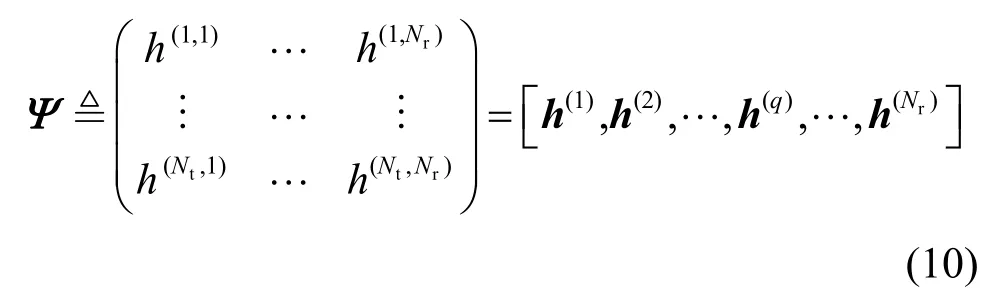
研究表明，采用抽头时延模型表示的MIMO-OFDM 无线信道在时域上呈现出稀疏性，即信道冲激响应向量h(p,q)的非零元素个数远小于向量长度。同时，MIMO 系统不同发射接收天线之间的子信道具有相似传播特性，可以认为所有子信道具有相同的支撑集，但抽头增益系数不同[15-16]。这样式(10)中Ψ的各个列向量可以视为稀疏向量且向量的非零元素位置相同。Ψ的这种性质也称为行稀疏性[17]。由于脉冲噪声在时域上持续时间较短，因此经过采样后形成的时域脉冲噪声向量u(q)中的非零元素个数远小于OFDM 符号长度，具有稀疏性特征。进一步地，不同接收天线之间距离比较小，这样当脉冲噪声出现时，可以认为所有接收天线会同时受到该脉冲噪声的干扰，所以经过采样后形成的时域脉冲噪声向量的非零元素位置相同，但非零元素的幅值不一定相同[11]。

从而式(9)可以写成如下形式

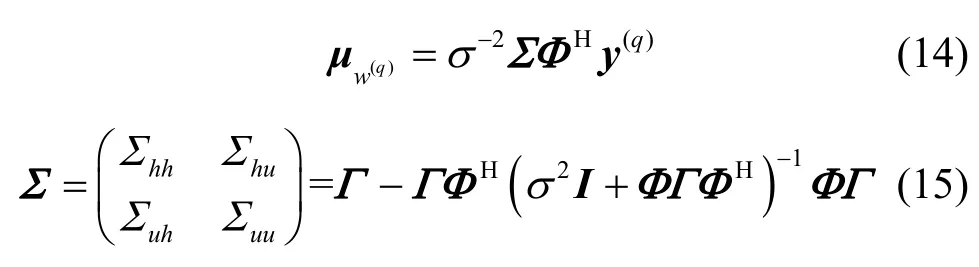
1) E-step。将W视作隐含变量，计算联合概率分布 Pr（Y,W;θ）在后验概率分布（由式(14)和式(15)求得）下的期望值Q（θ）其中，E{·}代表求期望，θ(k)代表第k次迭代求得的参数，ln（· ）代表自然对数运算。

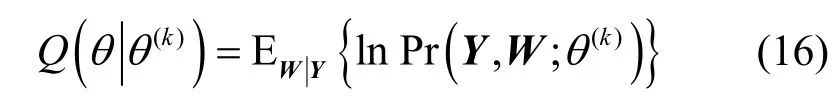
2) M-step。通过最大化期望值Q（θ）获得第k+1迭代的超参数估计值，即

将式(17)分别对γhi和γuj求导并设置导数等于零，求得第k+1 次迭代估计值为

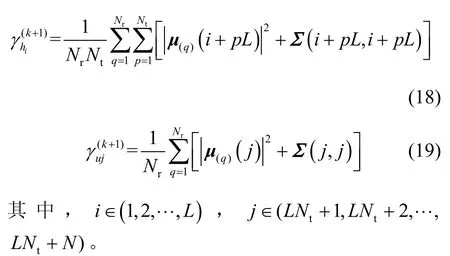
接下来求解超参数σ2，根据似然函数可以写出求解式为

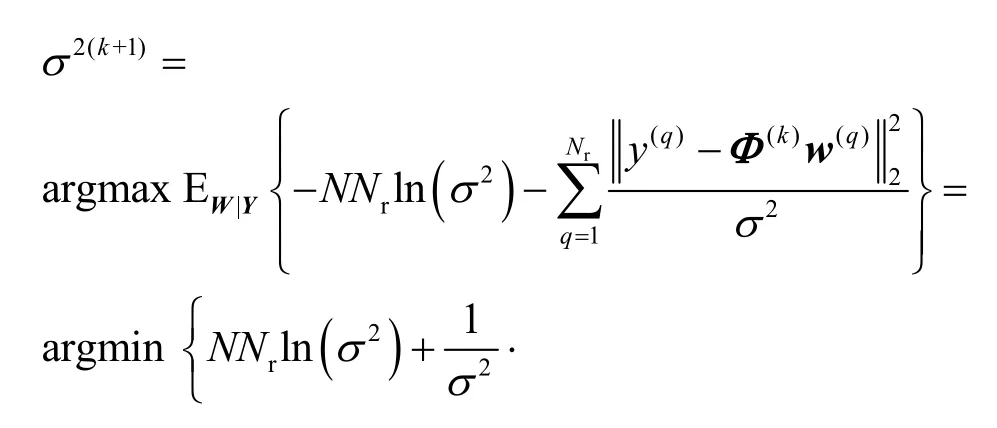
将式(20)对σ2求导并设置导数为零，得到第k+1 次迭代结果为

最后求解参数X，由于X中未知的参数实际是数据子载波上的发射符号，因此估计X相当于进行符号检测。根据似然函数，发射符号矩阵X的求解式可以写成

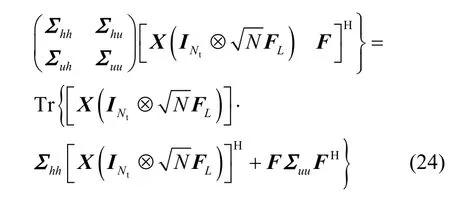
在式(24)中，将Σhu和Σuh所有元素设置为0，是因为考虑到实际中信道和脉冲噪声是独立且不相关的。结合式(23)和式(24)，式(22)可以写为

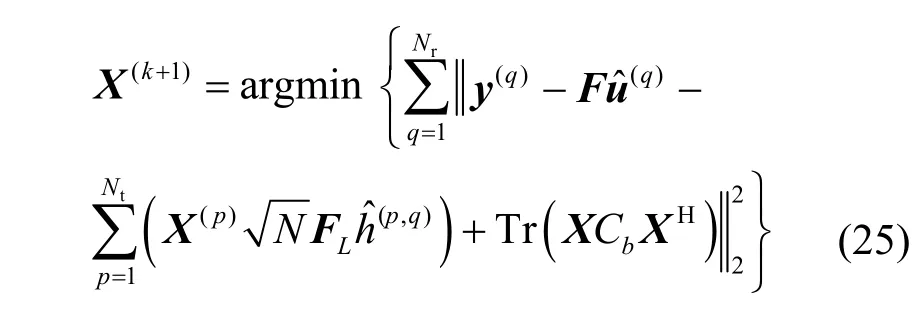
其中，Ω表示调制信号星座点集合，表示星座点集合元素数目，D表示数据子载波集合，x(p)(k)表示第p根发射天线上第k个子载波上的数据符号，y(q)(k)表示第q根接收天线上第k个子载波上的接收符号，F(k,:)表示矩阵的第k行。式(26)的求解可以通过穷举法实现，随着发射天线数目、调制信号星座点数目和子载波数据的增加，穷举法的运算复杂度会急剧增长，这时可以通过把式(26)转化为等效的MIMO信道，利用球形译码算法求解来降低运算复杂度[18]。

通过式(18)、式(19)、式(21)和式(26)求出第k+1 次迭代的超参数估计值Γ(k+1)、σ2(k+1)和X(k+1)后，将它们代入式(14) 和式(15) 计算新的后验均值和协方差矩阵Σ(k+1)，然后将更新后的后验均值和协方差矩阵求解新的超参数，这样反复迭代，直到达到收敛条件后停止。算法的伪代码如算法1 所示。

算法1同步符号检测的联合估计算法

残留脉冲噪声视作AWGN。同时根据信道CIR估计值计算每对天线之间的CFR 估计值

则第k个子载波上基于最大似然估计的符号检测算法可以表示为

其中，

式(29)可以使用现有球形译码算法进行求解，也可以使用其他MIMO 数据检测算法求解。

本文提出的同步符号检测的联合估计方法需要数据符号的初始估计值，如果随机选择容易导致算法不收敛。下面介绍如何利用MSBL 获得数据符号的初始估计值。根据式(12)，可以获得利用导频子载波和空子载波的信道与脉冲噪声联合估计压缩感知模型，如式(31)所示。

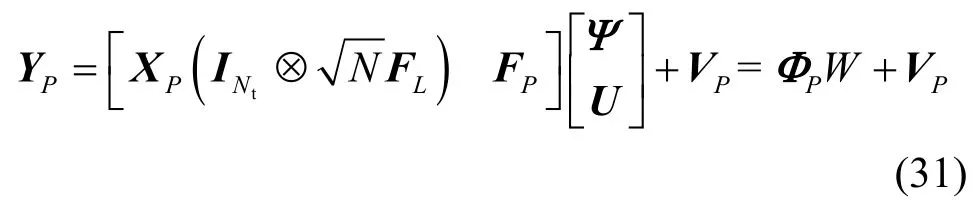
其中，YP、XP、FP、ΦP和VP分别由Y、X、F、Φ和V对应导频子载波和空子载波索引位置的行元素组成。式(31)中的观测矩阵ΦP没有未知元素，因此可以直接使用MSBL 算法估计W，从而获得每对天线之间的CIR 向量的估计值和每根接收天线上采样到的脉冲噪声估计值后，根据式(27)～式(29)利用球形译码算法获得数据符号的初始估计值X(0)。

3.3 方法复杂度分析

本文提出的同步符号检测的联合估计方法主要分为2 个阶段。第一阶段利用式(31)获得数据符号的初始估计值，这个阶段的运算复杂度为第二阶段利用式(12)联合估计信道和脉冲噪声，每一次迭代需要计算式(14)、式(15)、式(18)、式(19)、式(21)、式(26)的运算，其中每一个计算式的运算复杂度如表1 所示。根据表1 的分析，第二阶段的总运算复杂度可以写为，因此本文提出的同步符号检测的联合估计方法总的运算复杂度可以写为

表1 每次迭代的运算复杂度分析

4 仿真结果分析

本节利用数值仿真验证本文所提出方法的性能。一个2×2 MIMO-OFDM 系统仿真参数[16]如表2所示，其中每对天线之间的仿真信道参数设置基于ITU-R Vehicular B 信道模型，抽头数为6，均具有Jakes 功率谱，信道抽头增益归一化到1。每根接收天线上的总噪声（脉冲噪声与AWGN 之和）分别利用三元高斯混合模型（GMM,Gaussian mixture model）[8]和米德尔顿类A（MCA，Middleton class A）模型[8]实现。系统的信噪比定义为归一化后发射符号功率与系统总噪声功率的比值，即本文信道估计的性能指标采用均方误差（MSE，mean square error）表示，即脉冲噪声估计的MSE 性能指标为

表2 OFDM 系统仿真参数

4.1 信道估计结果

本文提出的信道和脉冲噪声（即干扰）联合估计方法与其他信道估计方法的信道估计误差性能随信噪比变化的对比如图2 所示。同步符号检测的联合估计和基于MSBL 的联合估计分别代表式(12)和式(31)对应的联合估计方法。基于MSBL 的信道估计代表传统基于压缩感知的信道估计方法，将脉冲噪声视作AWGN，没有对脉冲噪声进行抑制。基于MSBL 的信道与干扰独立估计首先采用基于空子载波构建压缩感知模型并通过MSBL 算法重构脉冲噪声[11]，再用MSBL 算法基于导频子载波估计信道。基于文献[16]的信道估计是一种联合数据检测和信道估计的方法，将脉冲噪声视作AWGN，没有对脉冲噪声进行抑制。基于文献[16]的信道与干扰独立估计方法首先基于空子载波构建压缩感知模型并通过MSBL 算法重构脉冲噪声后去除，再用文献[16]的信道估计方法估计信道。本文将文献[16]提出的方法作为对比来验证利用全部子载波信息可以改进仅利用导频和空子载波的估计方法的性能。为了验证脉冲噪声分别对信道估计性能的影响，分别在高斯混合模型和米德尔顿类A 模型2 种场景下进行了仿真。2 种脉冲噪声分布的参数如表2 所示。

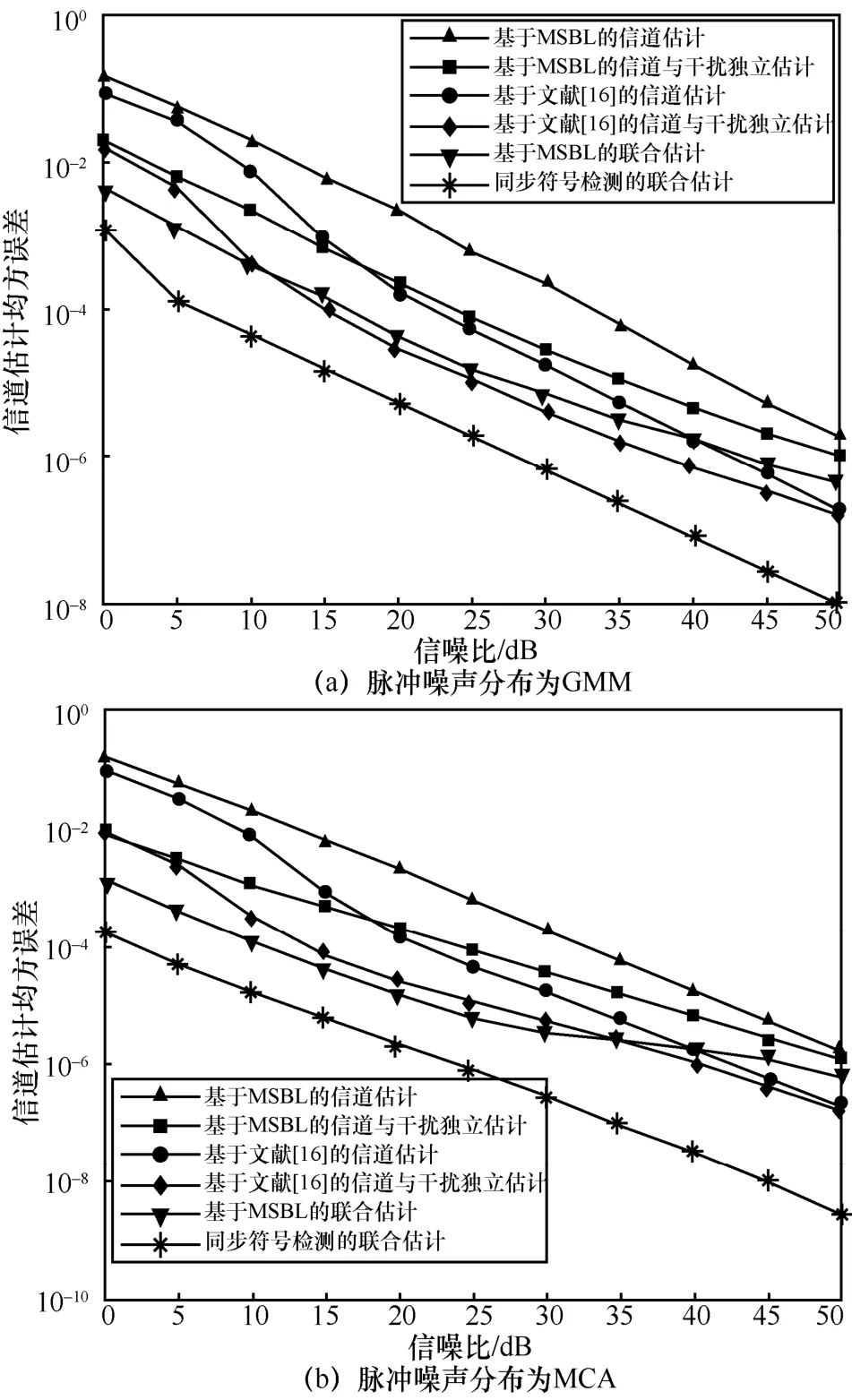
图2 信道估计误差性能对比

从图2 中可以看出，消除脉冲噪声能有效提升信道估计方法的性能，基于MSBL 的信道估计方法在消除脉冲噪声后性能提升了约10 dB，基于文献[16]的方法在消除脉冲噪声后性能提升了约8 dB。基于MSBL 的信道与联合估计方法与基于MSBL 的信道与脉冲噪声独立估计方法相比，性能提升了约8 dB，这说明同样仅利用导频和空子载波的信息，联合估计方法的性能要明显优于信道与脉噪声独立估计的性能。进一步分析可以看出，联合数据检测的信道估计方法性能要明显优于仅利用导频和空子载波的信道估计方法。在高信噪比场合下，先消除脉冲噪声后，文献[16]提出的信道估计方法比基于MSBL 的联合估计方法性能提升了1～2 dB。而本文提出的同步符号检测的联合估计方法与基于MSBL的联合估计方法相比，信道估计性能提升了约10 dB。性能改善的主要原因在于，本文提出的方法能利用OFDM 接收符号全部子载波上的信号来联合估计信道和脉冲噪声，因此显著增加了观测信号的维度，从而改善了稀疏信号的重构性能，使本文提出的信道估计方法性能明显优于现有仅利用导频和空子载波的估计方法。

对比图2(a)和图2(b)，在不同的脉冲分布下基于MSBL 的联合估计在高信噪比情况下变得平缓，并且性能略差于传统方法。其原因在于随着信噪比提升，脉冲噪声幅值逐渐减少，导致通过MSBL 联合估计方法重构脉冲噪声的精度不断下降，进而影响信道估计精度。相反传统方法由于信道估计与脉冲噪声估计单独进行，脉冲噪声估计的误差作为AWGN 影响后续的信道估计，因此随着信噪比增加信道估计性能可以保持下降趋势。而本文提出的同步符号检测的联合估计方法通过利用全部子载波上的接收信号作为观测信号，保证了随着信噪比的增加信道估计性能仍旧保持稳定的下降趋势。

4.2 脉冲噪声估计结果

同步符号检测的联合估计、基于MSBL 的联合估计和基于MSBL 的单独估计的脉冲噪声估计性能对比如图3 所示。

图3 脉冲噪声估计性能对比

基于MSBL 的单独估计只能利用空子载波上的接收信号重构脉冲噪声，基于MSBL 的联合估计可以联合利用导频子载波和空子载波上的接收信号重构脉冲噪声，本文提出的同步符号检测的联合估计可以利用全部子载波上的信号重构脉冲噪声。由于观测信号维度的增加，3 种基于MSBL 的脉冲噪声估计方法性能依次提升，这与压缩感知理论是一致的。随着信噪比提升，同步符号检测的联合估计的脉冲噪声估计性能一直保持稳定的下降趋势。而基于MSBL 的联合估计的下降趋势变得平缓。

4.3 误比特率结果

本文提出的方法与其他方法的误比特率性能对比如图4 所示，采用的MIMO 数据检测算法是球形译码算法[1]。此外作为基准，在假设信道状态信息已知情况下，图4 中同时展示了脉冲噪声未去除和完全去除2 种场景下的误比特率性能，其中，信道已知且干扰未去除代表在接收端信道参数已知，但脉冲噪声没有去除；信道已知且干扰去除代表在接收端信道参数已知，且脉冲噪声已经去除。从图4中可以看出，本文提出的基于MSBL 的联合估计方法优于其他方法，与基于文献[16]的信道与干扰独立估计方法相比性能提升了约2 dB。这个现象与上面的信道估计结果有差别，原因在于利用空子载波的脉冲噪声估计方法导致系统残留较多脉冲噪声，影响后续的符号检测，导致误比特率性能比基于MSBL 的联合估计方法较差。通过同步符号检测进而利用全部子载波信息来提高信道和脉冲噪声的联合估计准确性，提出的同步符号检测的联合估计方法的误比特率性能较仅利用导频和空子载波的联合估计方法相比进一步提升了2～4 dB，与信道已知且脉冲噪声完全去除这种理想情况下的性能相差1～2 dB。在不同的脉冲噪声分布下，本文提出的方法仍旧保持相似的性能优势。

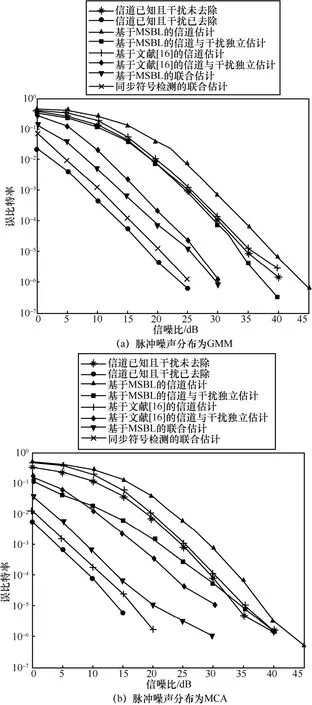
图4 误比特率性能对比

4.4 迭代性能分析

由于本文提出的同步符号检测的联合估计方法属于迭代算法，为了评估迭代次数对性能的影响，图5 通过仿真展示了信道估计性能和脉冲噪声估计性能随着迭代次数的变化趋势，信噪比为20 dB，脉冲噪声为混合高斯分布。从图5 中可以看出，迭代次数达到50 次以后，基于MSBL 的联合估计性能基本达到稳定，而同步符号检测的联合估计性能在迭代次数为30 次以后就基本稳定。本文在前面的仿真中，迭代次数设置为50 次。

图5 同步符号检测的联合估计方法的收敛性分析

5 结束语

本文通过分析MIMO-OFDM 系统信道与脉冲噪声的稀疏性特征，将信道与脉冲噪声的估计转换为一个多测量向量压缩感知模型，同时将发射数据符号视作未知参数，基于MSBL 和EM 算法设计了一种能同步符号检测的信道与脉冲噪声联合估计方法。本文提出的方法通过利用所有子载波上的信号作为观测信息，不仅提高了脉冲噪声估计性能，也改善了脉冲噪声环境下的信道估计性能。仿真结果表明，该方法在信道估计性能和误比特性能上都有明显提升。