基于身份的可穿刺签名方案
2022-01-12杨冬梅陈越魏江宏胡学先
杨冬梅,陈越,魏江宏,胡学先
(信息工程大学数据与目标工程学院,河南 郑州 450001)
1 引言
在基于公钥基础设施的密码体制中,权威机构通过数字签名为用户颁发公钥证书,保证了用户公钥的真实性和可信性。与此同时,用户证书的颁发、存储和撤销以及认证核查等工作也带来了繁重的管理开销。为此,Shamir[1]在1984 年首次提出了基于身份的签名(IBS,identity-based signature)方案,即以用户的个人信息(如身份证号、手机号、电子邮箱地址等)作为其公钥,而用户私钥由一个密钥生成中心利用系统主密钥来生成,签名的验证也只需要签名用户的公钥对所对应的身份信息,从而避免了对公钥基础设施的依赖。
随后,围绕IBS 方案安全性增强、效率提升和功能扩展等方面,密码学者提出了很多新的IBS 方案,如Cha[2]给出了完整的IBS 方案和该方案在随机预言模型下的安全性证明,Paterson 等[3]在标准模型下构造了第一个高效的IBS 方案,杨小东等[4]提出了强不可伪造的基于身份服务器辅助验证签名方案,刘翔宇等[5]提出了第一个紧致安全的IBS 方案,田苗苗等[6]提出了格上基于身份的增量签名方案以及侯红霞等[7]提出了素数阶群上基于非对称对的身份基环签名。在这些传统的IBS 方案中,假设用户私钥都是绝对安全的。但在现实应用环境中,随着网络攻击手段的多样化,用户私钥泄露事件趋于高发。另一方面,一旦用户私钥被攻击者窃取,攻击者就可以产生任何消息的合法签名,导致用户之前生成的所有签名都将失效。
为降低数字签名方案中由私钥泄露所带来的损失,Anderson[8]在1997 年首次引入了前向安全数字签名方案的概念,即要求在用户私钥泄露后,之前所生成的签名是不能被伪造的,但他并没有给出具体构造。Bellare 等[9]在1999 年的美密会上首次对这种密码学原语进行了形式化定义,并基于RSA(Rivest Shamir Adleman)群上的整数分解问题给出了一个具体构造。随后,学者对前向安全的数字签名方案进行了大量而又深入的研究,提出了很多在安全性和效率方面具有各自优势的相关方案,如Itkis 等[10]提出了具有高效签名和验证效率的前向安全签名方案,Kozlov 等[11]给出了密钥能快速更新的前向安全签名方案,Libert 等[12]构造了不可信更新环境中前向安全的签名方案,Abdalla 等[13]对文献[9]方案的私钥规模进行了优化等。以上这些前向安全的数字签名方案均是基于公钥证书的。为避免对公钥基础设施的依赖,Yu 等[14]在IBS 中引入了前向安全性,形式化地定义了前向安全的基于身份签名方案,并给出了一个具体构造。
然而,如Green 等[15]所指出,上述传统的通过周期性更新密钥实现前向安全性的方法不够灵活,导致其在实际部署中不可用。具体而言,传统的前向安全IBS 方案[14]以固定的时间周期为单位(如每小时、每天等)更新用户私钥,这导致当前时间周期的私钥泄露之后,攻击者仍能伪造当前时间周期内的签名。此外,传统的前向安全IBS 方案采用二叉树结构管理用户密钥和时间周期,使这些方案的密钥更新效率较慢。
为克服已有前向安全IBS 方案在密钥更新灵活性和效率方面存在的不足,本文提出了基于身份的可穿刺签名(IBPS,identity-based puncturable signature)方案。这种新的签名方案实现了细粒度的前向安全性,即每当用户完成对某个消息的签名之后,立即对私钥进行更新,使更新后的私钥不能再用来对同样的消息进行签名,保证了私钥泄露之前所生成签名的安全性。本文主要贡献总结如下。
1) 对传统的IBS机制进行了扩展,给出了IBPS机制的形式化定义,并通过安全模型刻画了这种签名方案的存在不可伪造性。
2) 将基于布隆过滤器的可穿刺公钥密码方案的构造思想应用到IBS,基于Paterson 等[3]的IBS方案构造了一个具体的IBPS 方案,其密钥更新过程只需进行一次布隆过滤器中的元素删除操作。
3) 基于计算性Diffie-Hellman(CDH,computational Diffie-Hellman)假设,在随机预言模型下证明了所构造IBPS 方案满足存在不可伪造性,并通过仿真实验展示了方案的实际性能。
2 相关工作
Yu 等[14]基于Waters[16]提出的基于身份加密方案,利用二叉树结构首次构造了前向安全的IBS 方案。在这种构造中,系统的生命周期被离散化为N个子周期,通过单向地周期性更新私钥和删除前一周期的私钥,用户可以在每个时间周期内使用不同的私钥,从而实现了前向安全性。沿用类似的方法,魏江宏等[17]提出了前向安全的密文策略基于属性加密方案;Wei 等[18]在前向安全IBS 的基础上通过用户撤销引入了后向安全性;Oh 等[19]进一步考虑了系统主密钥泄露的问题,提出了能同时抵抗用户私钥泄露和系统主密钥泄露的IBS 方案;杨小东等[20]在标准模型下提出了可撤销的基于身份的代理重签名方案。
事实上,上述方案的构造方法在一定程度上源于前向安全的公钥加密方案[21],因此也就继承了其局限性。为实现更实用的细粒度前向安全性,Green等[15]提出了可穿刺公钥加密方案的概念,并基于支持非单调访问结构的基于属性加密方案构造了具体的可穿刺公钥加密方案。随后,Wei 等[22]构造了密文长度固定的可穿刺的基于身份加密方案。为提高可穿刺加密方案中私钥穿刺的效率,Derler 等[23]进一步提出了布隆过滤器加密方案,并基于不同密码学原语给出了多种构造方案。
类似于可穿刺的公钥加密方案,可穿刺签名方案同样能提供签名的细粒度前向安全性,由Bellare等[24]首次提出。但是,他们给出的通用构造依赖于不可区分混淆和单向函数,具有较高的计算开销,在实际中不可用。Halevi 等[25]虽然也提出了一个可穿刺签名方案,但是需要在私钥穿刺操作后更新公钥,带来了较大的公钥管理负担。Li 等[26]基于布隆过滤器加密方案构造了具有较高穿刺效率的可穿刺签名方案,并将其应用到了区块链中的权益证明协议。
3 预备知识
3.1 布隆过滤器
布隆过滤器[27]是一种经典的随机数据结构,通过一个简短的二进制序列T来表示一个集合S,并能高效地判定一个元素s是否属于该集合。具体而言,在集合S 上进行查询时,若s∈S,则以概率1 返回1,表示s确实在集合S 中;若s∉S,则以概率1-δ返回0,表示s不在集合S 中,其中δ为假阳性概率,即当s∉S 时,仍以δ的概率返回1。
定义1布隆过滤器[27]。令U 为元素取值空间,其上的布隆过滤器 B=(BFGen,BFUpdate,BFCheck) 由3 个子算法组成,具体定义如下。
BFGen (ℓ,k),生成算法。以2个正整数 ℓ,k∈N为输入,首先选择k个一般的Hash 函数H1,…,Hk,其中Hj:U→[ ℓ],并令(长度为ℓ 且各个位置均为0 的字符串),最后输出(H,T)。
BFUpdate (H,T,u),更新算法。以Hash 函数族过滤器当前状态T∈{0,1}ℓ和一个元素u∈U 为输入,首先令T′←T,然后对任意的整数j∈ [k],令T′[H j(u)]=1,其中T′[i]表示T′的第i位,最后返回更新后的过滤器状态T′。
BFCheck (H,T,u),检验算法。同样以Hash函数族过滤器的当前状态T∈{0,1}ℓ和一个元素u∈U 为输入,然后计算并输出一个比特
如上定义的布隆过滤器具有完善的完备性、假阳性概率有界、集合表示紧致等特性。
3.2 双线性映射与CDH 假设
定义2双线性映射。令G 和GT是2 个阶为p的乘法循环群,其中p是一个长度为λ(安全参数)的素数,令g为G 的随机生成元,则双线性映射e:G × G →GT满足下述条件的映射。
1) 双线性:对任意的群元素x,y∈G 和任意的整数a,b∈Zp,e(x a,yb)=e(x,y)ab均成立。
2) 非退化性:e(g,g) ≠ 1。
3) 可计算性:对任意的群元素x,y∈G,存在一个多项式时间算法能有效计算出e(x,y)。
为方便描述,用一个五元组 (G,GT,g,p,e)来表示如上定义的双线性映射。进一步,定义在群G 上的CDH 问题是指,给定群元素g a,gb∈G,要求计算gab,其中是随机选取的整数。
定义3CDH 假设。对于任意一个概率多项式时间的攻击者A,给定g a,gb∈G,若其输出gab的概率是λ的可忽略函数,则称CDH 假设在群G 上成立。
4 可穿刺的IBS 方案定义
4.1 形式化定义
IBPS 方案可看作一般的IBS 方案在安全性方面的增强,也可看作可穿刺签名方案针对无公钥基础设施情形下的扩展。粗略而言,可穿刺的签名方案比一般签名方案多了一个私钥穿刺算法,即当用户的私钥在每签名完一个消息后,需要利用该消息在用户私钥上进行穿刺操作,以防用户私钥被再次用来产生该消息的签名。
通过结合一般的IBS 方案[3]和可穿刺加密/签名方案[23,26]的形式化定义,下面给出IBPS 方案的形式化定义,共由5 个多项式时间的算法组成。
Setup()λ,系统建立算法。输入系统安全参数λ,输出系统公开参数pp 和系统主密钥msk。
Extract(pp,msk,ID),私钥提取算法。输入系统公开参数pp、系统主密钥msk 和用户身份ID,输出相应的初始私钥skID。
Punc(pp,skID,m),私钥穿刺算法。输入系统公开参数pp、用户的当前私钥skID和一个用该私钥签名过的消息m,输出一个更新过的私钥sk′ID,此时也称sk′ID是被消息m穿刺过的私钥。
Sign(pp,skID,m),签名算法。输入系统公开参数pp、用户当前私钥skID和待签名消息m,输出对消息m的签名σ。
Verify(pp,σ,m,ID),验证算法。输入系统公开参数pp、签名σ、签名消息m和用户身份ID,当σ是一个关于ID 和m的有效签名时输出1,否则输出0。
一个IBPS 方案是正确的是指,对任意按正确方式生成的公开参数和主密钥(pp,msk)←Setup(λ)、任意用户初始私钥skID←Extract (pp,msk,ID)以及任意签名消息集M={m1,…,mq}和签名消息m∈M,有

总成立。对反复穿刺q次后的用户私钥Punc(pp,skID,mi)(i∈ [q]),只要签名消息m∉M,则
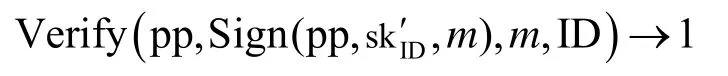
总成立。
4.2 安全性定义
为定义IBPS 方案的存在不可伪造性,在安全模型中给攻击者提供了私钥提取询问、签名询问和私钥穿刺询问。此外,为刻画前向安全性,还允许攻击者询问挑战者身份所对应的私钥,但所返回的私钥必须是被挑战消息穿刺过的。具体而言,IBPS方案的存在不可伪造性通过一个挑战者C 和一个敌手A 之间的安全游戏来定义,主要包含以下3 个阶段。
系统建立阶段。给定安全参数λ,挑战者C 运行系统建立算法Setup(λ)→(pp,msk),然后将系统公开参数pp 发送给敌手A,而自己持有系统主密钥msk。同时,挑战者C 初始化4 个空集
询问阶段。在该阶段,敌手A 可以自适应地进行以下3 种询问。
1) 私钥提取询问。敌手A 向挑战者C 提交一个用户身份ID,要求挑战者C 返回相应的私钥skID。接收到该询问后,挑战者C 直接运行私钥提取算法Extract(pp,ms k,ID)→skID,同时更新集合Qsk←Qsk∪{ID},然后将skID发送给敌手A。
2) 签名询问。敌手A 向挑战者C 提交一个用户身份ID 和消息m,要求挑战者C 返回相应的签名σ。挑战者C 首先调用私钥生成算法Extract(pp,msk,ID) →skID,然后运行签名算法Sign(pp,skID,m)→σ,同时更新集合Qsig←Qsig∪{(ID,m)}和Qσ←Qσ∪{σ},最后将签名 发送给敌手A。
3) 穿刺询问。敌手A 向挑战者C 提交一个用户身份ID 和消息m,要求挑战者C 返回相应被m穿刺过的用户私钥为此,挑战者首先通过调用私钥生成算法产生用户的初始私钥,即Extract(pp,ms k,ID)→skID,然后调用私钥穿刺算法Punc(pp,skID,m)→同时更 新集合Qpunc←Qpunc∪{(ID,m)},最后将穿刺过后的私钥sk′ID发送给敌手A。
伪造阶段。敌手A 结束询问阶段之后,输出一个关于(m*,ID*)的签名σ*。
若以下条件同时满足,则称敌手A 赢得了上述安全性游戏。

定义4IBPS 的存在不可伪造性。对任意一个针对IBPS方案的概率多项式时间敌手A,若其赢得上述安全游戏的概率是λ的一个可忽略函数,则称该IBPS 方案满足存在不可伪造性。
本文考虑一种较弱的存在不可伪造性,即选择性存在不可伪造性,要求敌手A 在开始安全性游戏之前就将挑战消息m*提交给挑战者C。
5 方案具体构造
基于Paterson 等[3]的IBS 方案,本节给出一个具体的IBPS 方案构造,其核心在于如何实现用户密钥的穿刺操作。为此,本文借鉴Derler 等[23]提出的密钥穿刺机制,利用布隆过滤器来管理用户私钥和签名消息。具体而言,在生成用户私钥时,先初始化一个布隆过滤器(H,T)←BFGen(ℓ,k),然后对于T的每一个位置i∈[ ℓ ],生成一个相应的私钥构件ski;在对消息m进行签名时,首先利用H将其映射到T的k个位置,从中选取一个满足T[i′] ≠ 1的位置i′,然后利用相应的用户私钥构件进行签名;在完成对m的签名之后,将m添加到布隆过滤器中并更新其状态BFUpdate(H,T,m)→T′,同时,在所有满足T′[i]=1的位置,将相应的用户私钥构件设置为ski←⊥。可以看出,通过上述密钥穿刺过程,用户私钥不能对已签名过的消息进行再次签名。具体构造的IBPS 方案由以下5 个算法组成。
Setup(λ)。给定系统安全参数λ之后,系统建立算法首先生成双线性群 (G,GT,g,p,e);然后,分别定义用户身份标识空间ID={0,1}γ和签名消息空间M={0,1}η,选择 2 个 Hash 函数H:{0,1}*→{0,1}γ和H′:{0,1}*→{0,1}η,以及另外一个 Hash 函数H~ :N →G ;选择随机群元素g2,u0,vo∈G,以及2 个随机向量u=(u1,… ,uγ)∈Gγ和v=(v1,…,vη)∈Gη;最后,选择一个随机整数α∈Zp,计算g1=gα,并令系统主密钥为系统公开参数为pp={(G,GT,g,p,e),
Extract(pp,msk,ID)。给定系统公开参数pp、系统主密钥msk 和用户身份ID∈{0,1}*,私钥提取算法首先将ID 映射到系统定义的身份标识空间,即令θ=H(ID)=(θ1,…,θγ) ∈{0,1}γ;然后,初始化一个布隆过滤器(H,T)←BFGen(ℓ,k),其中T=0ℓ;选择随机整数r1,r2∈Zp,对任意整数i∈[ℓ ],按如下方式计算私钥构件ski。
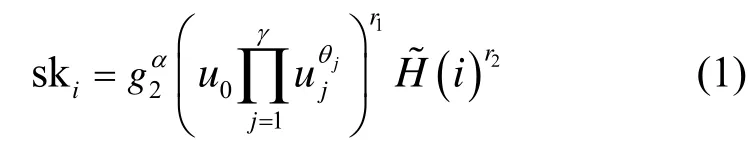
最后,按照如下结构输出用户私钥。

Punc(pp,skID,m)。给定系统公开参数pp、用户的当前私钥和一个消息m∈{0,1}*,令ω=H′(m)=(ω1,…,ωη)∈{0,1}η;然后,将消息m添加到布隆过滤器的集合中,并对其状态进行更新,即令T′←BFUpdate(H,T,m);对任意i∈[ ℓ ],按照如下方式对相应的私钥构件进行更新。

Sign(pp,skID,m) 。给定公开参数pp、用户当前私钥和待签名消息m,若BFCheck(H,T,m)→1,则输出错误符号⊥,否则,存在一个指标i*∈{i1,… ,ik}使其中i j=H j(m)(j∈ [k]);令ω=H′(m)=(ω1,…,ωη),选取随机指数rm∈Zp,计算
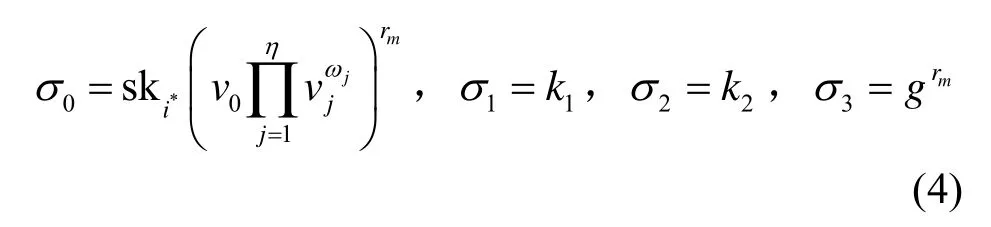
最后,返回签名σ={i*,σ o,σ1,σ2,σ3}。
Verify(pp,σ,m,ID)。给定公开参数pp、签名σ={i*,σ o,σ1,σ2,σ3}、消息m和用户身份ID,首先令θ=H(ID)=(θ1,…,θγ)和ω=H′(m)=(ω1,…,ωη);然后,验证下述等式是否成立。
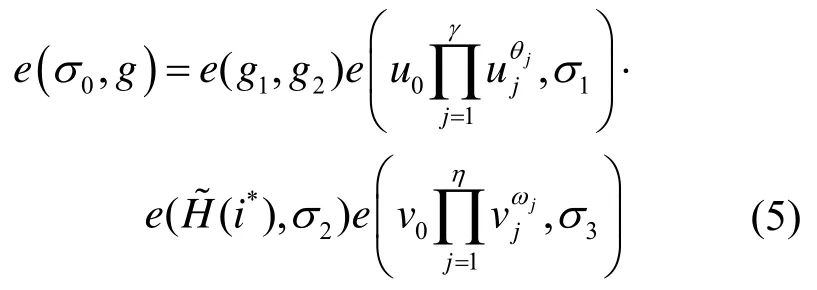
若等式成立,则说明σ是一个关于ID 和m的有效签名,输出1;否则输出0。
方案正确性依据私钥生成算法可知,私钥构件sk*i的值为将其代入式(5)可得
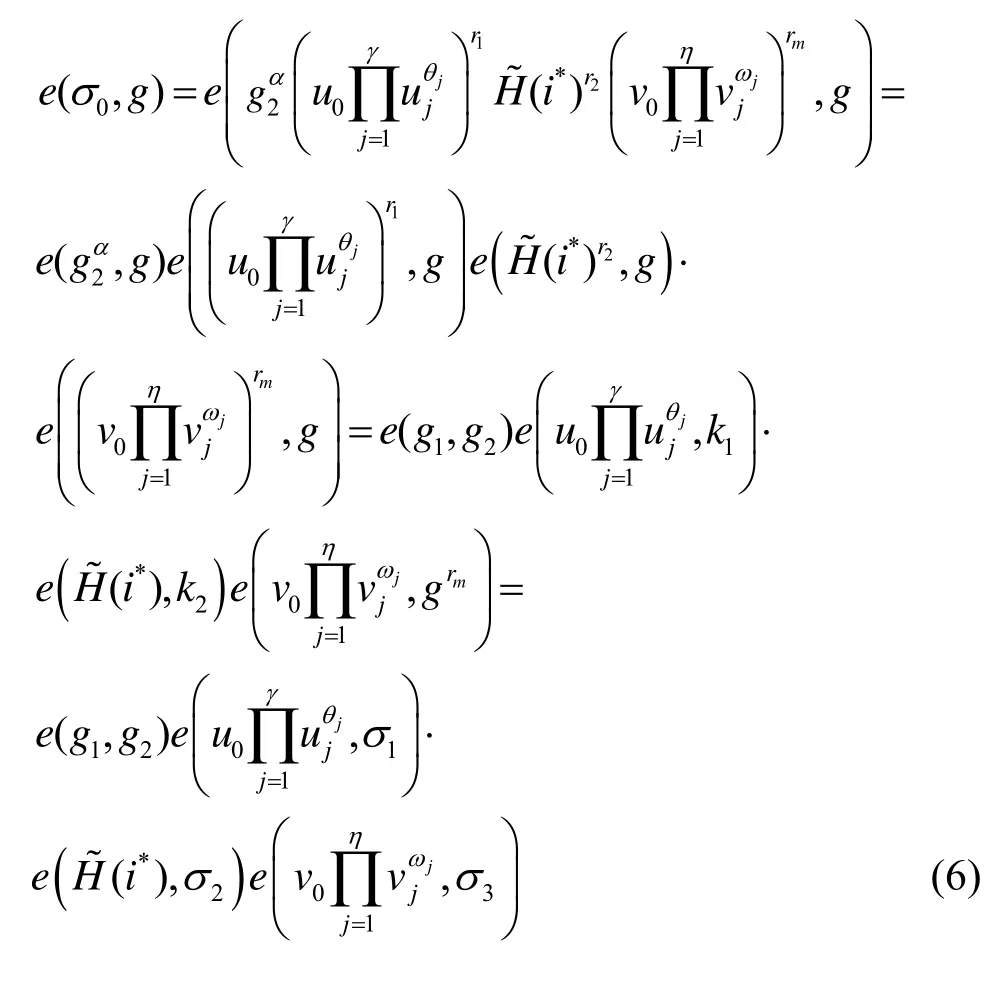
6 安全性证明及性能分析
6.1 安全性证明
定理1IBPS 方案安全性。对于依据安全参数λ生成的双线性群 (G,GT,g,p,e),若CDH 假设在群G 上成立,则所构造的IBPS 方案在随机预言模型下满足选择性的存在不可伪造性。具体地,有
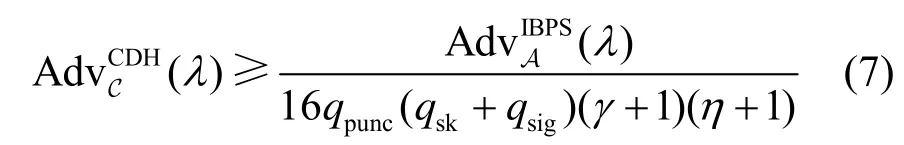
其中,qpunc是私钥穿刺询问次数,qsk是私钥提取询问次数,qsig是签名询问次数。
证明为证明定理1,主要采用Waters[16]提出的证明技巧,同时以随机预言机的方式模拟Hash函数对其进行扩展。下面,给出挑战者C 模拟安全性游戏各个阶段的细节。
系统建立阶段在初始阶段,挑战者C 收到一个双线性群 (G,GT,g,p,e),以及群G 上CDH 问题的实例(g a,gb),其中a和b是选自中的随机整数,C 的目标是计算出gab。此外,敌手A 需在安全性游戏开始之前提交挑战消息m*。

在上述定义的基础上,按如下方式设置所构造IBPS 方案的系统公开参数
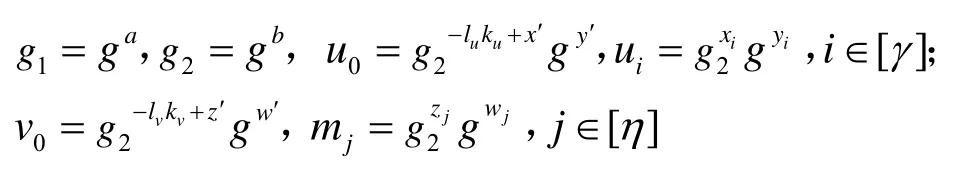
最后,C 初始化4 个空集Qsk←∅、Qsig←∅、Qσ←∅和Qpunc←∅,并将按照上述方式生成的系统公开参数发送给攻击者A,同时还向其提供Hash 函数的查询服务。
询问阶段在该阶段,A 可以自适应地进行私钥提取查询、签名查询和私钥穿刺查询,这3 种询问同时还涉及Hash 函数H,H′,的询问。对于H和H′,挑战者将它们模拟成一般的抗碰撞Hash函数。对于Hash 函数,挑战者C 按照如下方式进行模拟:对任意i∈[ ℓ ],选择一个随机整数ti∈Zp,若有i∈{H j(m*):j∈[k]},则直接令否则令下面给出C 响应3 种查询的方式。
1) 私钥提取询问。给定一个用户身份ID,C 先令H(ID)=(θ1,…,θγ),此时H被模拟成一个一般的抗碰撞Hash 函数。进一步,若有F(ID)=0 modp,则C 终止模拟,否则C 选择随机整数令然后,C 计算ID 所对应的私钥构件ski

从式(8)中可以看出,尽管C 不知道系统主密钥,但上述私钥构件对其都是可计算的,并且与按照真实的私钥提取算法所产生的私钥是同分布的。最后,C 将ID 的私钥发送给敌手A,同时更新集合
2) 签名询问。给定用户身份ID 和待签名消息m,挑战者C 首先将它们映射到相应的二进制字符串,即此时若有则C 通过调用私钥提取询问先生成相应的用户私钥skID,然后直接利用IBPS方案的签名算法即可生成关于ID 和m的正确签名,并返回给敌手A。另一方面,若F(ID)=0 modp且K(m)=0 modp,则C 终止安全性游戏,否则C 选择随机整数并令,然后按照下述方式生成签名
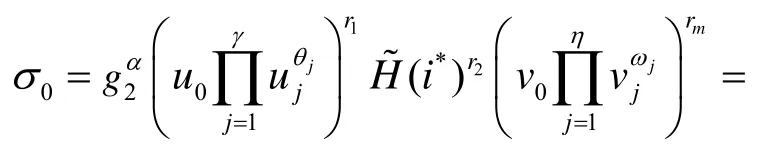

可以看出,上述签名构件对C 都是可计算的,且与IBPS 方案中的签名算法所产生的签名同分布。最后,C 将关于ID 和m的签名σ={i*,σ o,σ1,σ2,σ3}返回给敌手A,同时更新集合Qsig←Qsig∪{(ID,m)}和Qσ←Qσ∪{σ}。
3) 私钥穿刺询问。在响应该询问之前,挑战者C 先猜测敌手A 的第j次该询问是关于挑战身份ID*的查询,若猜测失败,则终止安全性游戏。对于关于其他用户身份的私钥穿刺询问,C 先调用私钥提取询问得到相应的用户私钥,然后利用IBPS方案的私钥穿刺算法即可得到穿刺后的私钥,并将其返回给敌手A。特别地,对于A 的第j次询问,由安全模型中对敌手的约束可知,此时A 提供的就是挑战身份ID*和挑战消息m*。为生成穿刺后的用户私钥,C 选择随机整数对任意i∈[ ℓ ],若,则令ski←⊥,否则按照下述方式计算ski
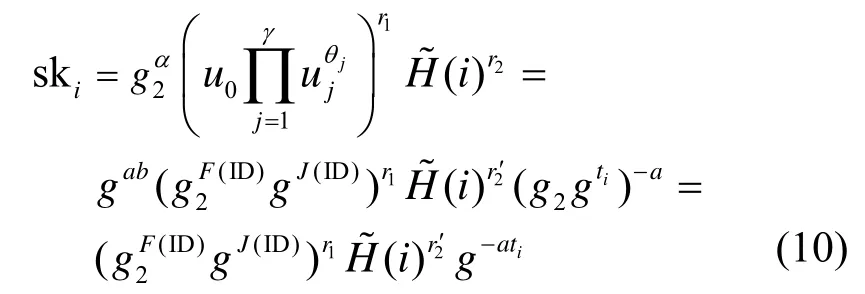
伪造阶段敌手A 结束询问阶段之后,输出一个关于(m*,ID*)的签名同时满足下述条件。

此时,若F(ID*) ≠0 modp或K(m*) ≠0 modp,则挑战者C 直接终止安全性游戏。最终,若挑战者C没有终止安全性优势,则可按照下述方式计算出gab。
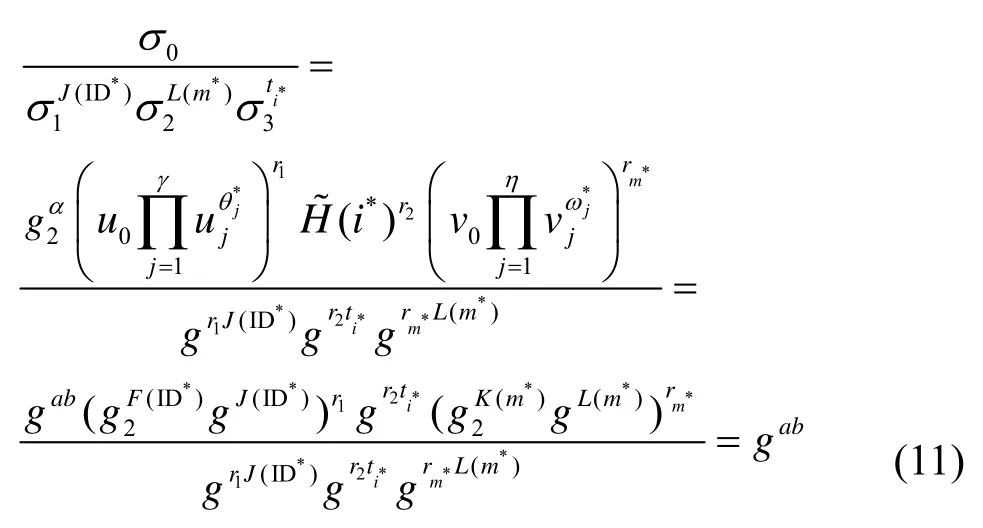
从而解决了给定的CDH 问题实例。
概率分析挑战者C 能计算出abg的前提是不终止安全性游戏,而由Waters[16]的“artificial abort”分析技术可得,C 不终止安全性游戏的概率为

6.2 性能分析
表1 给出了本文所提IBPS 方案与其他相关签名方案在计算开销和存储开销方面的比较。在比较过程中,用e 表示一次模指数运算,p 表示一次双线性对运算,γ表示用户身份的长度,η表示签名消息的长度,ℓ 表示布隆过滤器的数组长度,N表示时间周期总数,G 表示一个群元素。在比较过程中忽略运算时间非常小的Hash 运算。

表1 相关签名方案的计算/存储开销比较
从表1 中可以看出,相比于Paterson 等[3]的IBS 方案,本文所提IBPS 方案在私钥提取算法上具有较大的计算开销,这主要是由于为了实现细粒度的前向安全性,额外地为布隆过滤器所对应的二进制序列的每一个位置上都生成了一个私钥构件。另一方面,相比于Yu 等[14]的前向安全IBS方案,本文所提IBPS 方案的密钥穿刺/更新开销主要是Hash 运算和删除运算,几乎可以忽略,而Yu 等[14]的前向安全IBS 方案的密钥更新开销与总的时间周期数目成对数关系。此外,在存储开销方面,本文所提IBPS 方案的公开参数规模与Paterson 等[3]的IBS 方案相当,而Yu 等[14]的前向安全IBS 方案具有更大的公开参数规模。在签名长度方面,本文所提方案与Yu 等[14]的前向安全IBS 方案相同,均略高于Paterson 等[3]的IBS 方案。特别地,Yu 等[14]的前向安全IBS 方案的私钥规模与总的时间周期总数的对数成平方关系,具有较高的存储开销。
表2 给出了相关签名方案在安全性质方面的比较。从表2 可以看出,只有本文所提方案具有细粒度的前向安全性,但其安全性却是在随机预言模型下证明的,而非标准模型。此外,在安全性假设方面,Yu 等[14]方案的安全性基于一个更强的q-型Diffie-Hellman 指数困难性问题假设。

表2 相关签名方案的安全性质比较
6.3 仿真实验
为验证所构造IBPS 方案的实际性能,将其在Charm[28]框架下进行了实现,并测试了各个算法的实际运行时间。所有的测试实验均是在具有16 GB内存和i7-1160G7@1.20GHz CPU 的PC 上进行的。
在仿真实验中,布隆过滤器中的集合规模设置为n=220,即允许用户在一年中每天向其中添加 212个元素,同时布隆过滤器的假阳性概率设置为δ=10-3,表示布隆过滤器的字符串长度为ℓ=1.7 ×107,Hash 函数个数为k=10。在一般的前向安全IBS 方案中,设定总的时间周期数为N=219,即允许用户在一年的时间里每隔一分钟更新一次私钥。所采用的 Hash 函数均为SHA-256,椭圆曲线为Charm 提供的SS512 曲线和SS1024 曲线。
图1 给出了相关基于身份签名方案中各个算法运行时间对比。从图1 可以看出,本文所提IBPS方案的私钥抽取算法的运行时间要远高于其他2 个方案,但该算法一般都是离线运行且执行一次,故在实际中不影响系统性能。另一方面,本文所提IBPS方案的私钥更新效率非常高。具体地,在SS512 曲线下,私钥穿刺算法的运行时间仅有2.32 s,而Yu等[14]方案中算法的运行时间则接近350 s,比本文所提IBPS 方案高了近150 倍。
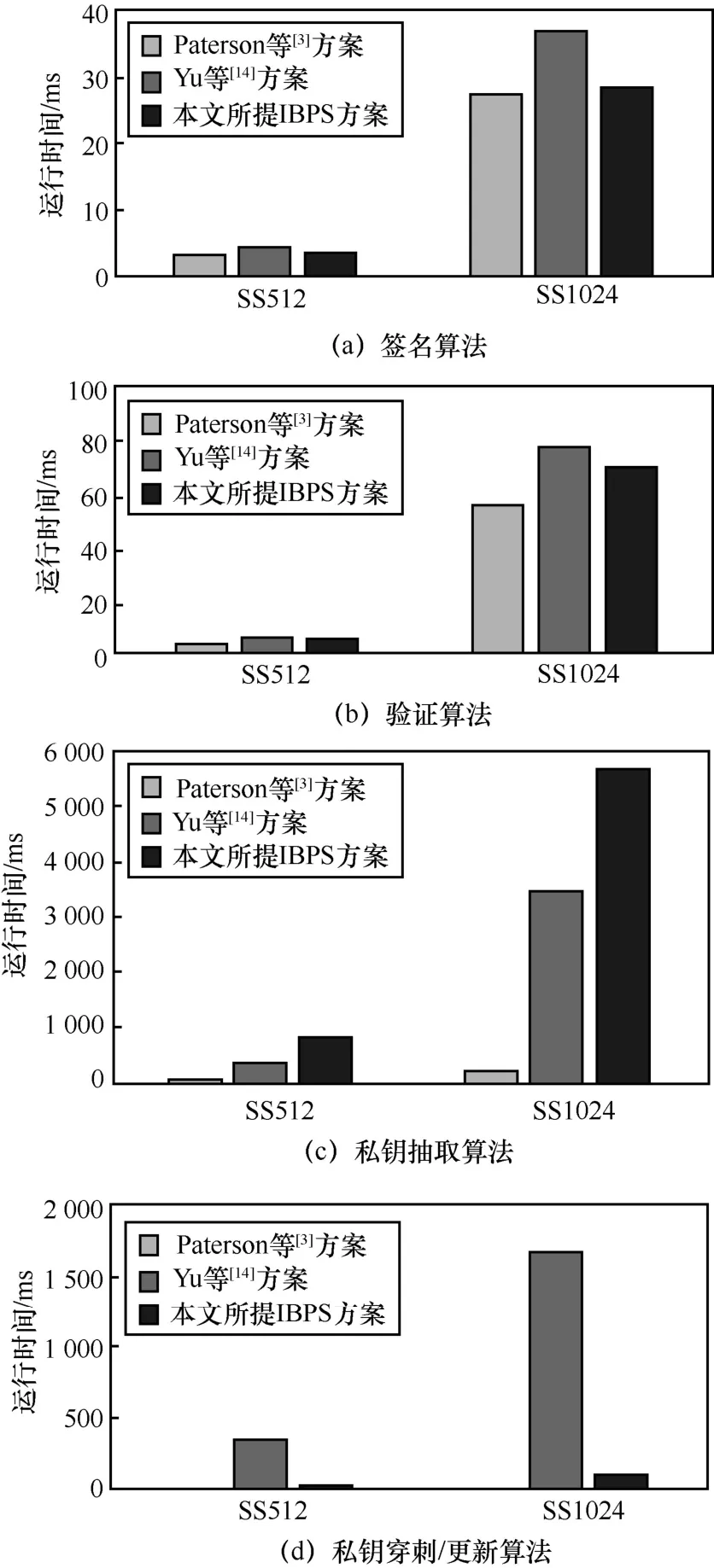
图1 相关基于身份签名方案中各个算法运行时间对比
图2 给出了相关IBS 方案的存储开销。从图2可以看出,由于产生了私钥构件的多个备份,本文所提IBPS 方案具有较大的私钥规模。

图2 相关IBS 方案的存储开销
6.4 方案应用
本文所提IBPS 方案可以在任何部署过IBS 的场景中使用,以增强用户私钥的前向安全性。下面以IBPS 在监控系统的应用为例,如图3 所示。目前的物联网技术和无线通信技术支持部署大规模的监控系统,物联网设备、智能手机、无线摄像头、无线相机等向云服务器提供视频和图像,即向监控系统提供监控数据。一个安全可靠的监控系统,应该做到设备提供的视频和图像确保是真实的,不是被修改或伪造的;设备需要诸如公钥证书等凭证来提供视频和图像的真实性;任何攻击或私钥泄露不会破坏所有以前的监控数据,即应当保证监控数据的前向安全。

图3 IBPS 在监控系统的应用
本文所提IBPS 方案为解决上述实际问题提供了可靠对策。图3 中的每个设备将其身份标识注册到云服务器,密钥服务器负责为每个设备分发与其身份标识对应的私钥,同时,把自己的公钥发送给云服务器。当设备发送数据时,先对数据签名,然后把签名和数据一起发送,而云服务器只接受其签名有效的数据。这样,一方面保证了数据来源的真实性,另一方面云服务器利用密钥服务器的公钥验证接收的数据,而设备不需要携带证书。每发送完一次数据,该设备都进行密钥穿刺操作,完成私钥的更新。这保证了任何设备在私钥泄露的情况下,该设备所有以前的签名仍然有效。
7 结束语
本文针对已有的前向安全的基于身份签名方案的灵活性不强、私钥更新效率较低的问题,通过引入可穿刺公钥加密思想,提出了基于身份的可穿刺签名方案。基于Paterson 等[3]的基于身份签名方案,利用布隆过滤器构造了一个具体的基于身份的可穿刺签名方案,以较高的存储开销为代价,实现了签名的细粒度前向安全性和用户私钥的高效更新。安全性证明表明,本文所提IBPS 方案在随机预言模型下满足存在不可伪造性。理论分析和实验结果表明,本文所提IBPS 方案在安全性和效率方面具有优势,更适合在实际应用中部署。
