伪斜工作面梯形采场的基本顶初次破断特征
2022-01-11张守宝李强刘志高皇甫龙王超
张守宝李强刘志高皇甫龙王超
中国矿业大学(北京)能源与矿业学院,北京 100083
在综采工作面开采中,根据特殊开采需要,为使工作面两端头开采进度不同,经常会人为布置伪斜工作面,在倾斜和急倾斜工作面进行伪斜布置,可以降低绝对倾角[1];在旋转工作面进行伪斜布置,可以实现顺利旋转。伪斜工作面顶板受力具有明显的非对称性[2]。顶板断裂时,在两端头形成大小不同的“弧形三角块”悬板,从而使两端头垮落步距大小不同。端头悬顶过长时,顶板会突然垮落,形成较强的矿压显现,还会将有害气体挤入工作面,影响工作面安全生产[3-4]。
关于综采工作面基本顶的破断,钱鸣高等[5]提出了矩形采空区顶板的“O-X”型破断,解释了基本顶初次来压时顶板的破断规律,并形成了砌体梁理论。何富连等[6]研究了以弹-塑性为基础边界的基本顶初次破断位置、破断顺序及全区域破断形态特征的影响因素和权重关系。杨胜利等[7]研究了基于中厚板理论的孤岛工作面初次来压和周期来压时关键层的位移及应力分布,讨论了不同厚度下基本顶的破断结构特征。左建平等[8]研究了不同厚度下基本顶的板破断模式,研制了采空区顶板破断模拟实验装置,提出基本顶破断除“O-X”型外,还存在“O-∗”型。房局[9]将急倾斜伪斜采场悬露顶板简化为均布荷载下的矩形板,计算得到了顶板岩层上下板面的最大主应力云图,分析了矩形顶板的破断形态为“O-X”和“C-X”型破坏。张兆一[10]利用弹性薄板理论建立了直角梯形薄板关键层模型,采用康托洛维奇变分近似法求解,得到两对边固支、两对边简支的直角梯形薄板关键层的弯曲下沉解析解,并给出了关键层发生剪切破断和拉伸破断的公式。
目前,对于采空区顶板破断的研究都是基于矩形条件下,而对非矩形采空区所形成的异形顶板研究较少。实际上当工作面伪斜布置时,采场顶板不再是矩形顶板,当工作面初次来压时,采空区顶板结构呈近似直角梯形,其破断垮落时工作面两端头悬顶距离会出现明显差异。中煤山西华昱能源有限公司南阳坡煤矿在伪斜工作面开采中发现,当采用伪斜布置时,上端头采空区悬顶长度达30 m,严重影响安全生产,不得不采用强制放顶控制顶板。因此,研究伪斜工作面顶板破断规律对指导工作面安全开采具有重要意义。
1 伪斜工作面梯形基本顶力学分析
1.1 研究工程背景及力学模型的选择
中煤华昱南阳坡煤业有限公司为年产超4 Mt的特大型矿井,该矿采用综采放顶煤回采工艺(采高3.2 m、顶煤厚度3 ~9 m)开采6 号煤,煤层倾角2°,埋深240 m。6106 工作面由外段和内段两部分组成,其中外段走向长660 m,倾向长110 m,巷道平面布置如图1 所示。在实际开采中为了实现工作面开采的内外衔接,采用伪斜布置工作面开采外段,但是在生产中出现了进风巷超前10 m 时悬顶距离过大的问题,必须研究伪斜工作面超前距离与基本顶垮落之间的影响规律。
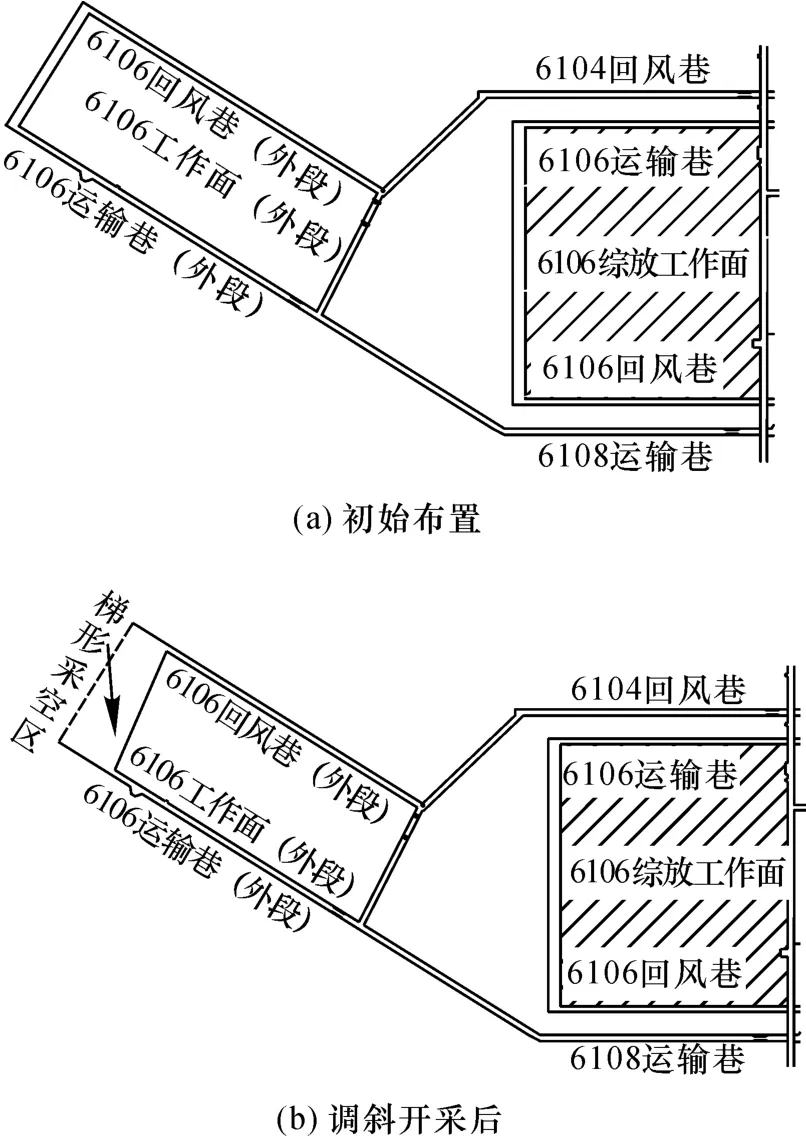
图1 6106 工作面布置平面Fig.1 Layout plan of working face 6106
基本顶破断和运移规律的力学模型有两类:一类是将矩形采场基本顶破断前结构简化为岩梁模型或板结构力学模型,以研究基本顶的破断规律、破断形态及来压步距等;另一类是基本顶破断后构成的“砌体梁”结构或传递岩梁力学模型[11-12]。
在弹性力学中,板结构中两个板面之间的距离称为板的厚度,而平分厚度的平面称为板的中面。如果中面的最小尺寸a(板的宽度)与板的厚度δ的比值大于8 时,称为薄板。在采矿工程中,工作面基本顶可以看作是板结构。南阳坡煤矿6106 工作面基本顶为厚度5.0 m 的中、粗粒砂岩,基本顶初次来压步距为50 m,所以有50/5=10,因此可以看作薄板来建立相应力学模型,以求解板的破断问题。6106 工作面(外段)顶板岩性情况见表1。

表1 煤层顶板岩性情况Tab.1 Lithology of coal seam roof
1.2 力学模型的建立
针对南阳坡煤矿6106 伪斜工作面的布置方案,在6106 工作面四周都未开采条件下,建立四边固支的梯形薄板力学模型(图2)。在弹性力学中对矩形薄板弯曲问题的求解基础上,对梯形薄板的挠度函数及内力方程进行推算。

图2 梯形薄板力学模型Fig.2 Mechanical model of trapezoidal thin plate
任意梯形或三角形薄板有着其特殊的变形性质。由于边界条件复杂,本文在前人[13-14]研究的基础上,结合康托洛维奇变分近似法及加权残数法对梯形薄板弯曲问题进行求解。
设板面分布均布荷载q的边界条件为

式中,ω为薄板挠度,一次导为薄板转角;s 为薄板边界。
根据弹性力学中对弹性曲面的求解,可以得到板弯曲的控制微分方程:
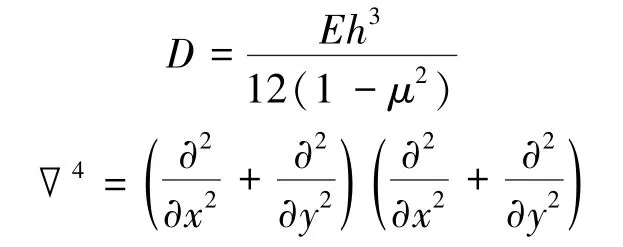
式中,D为板的抗弯刚度;∇4为双重调和算子。
从边界方程出发,给出特定弯曲试函数。设板的挠度近似函数[15]为
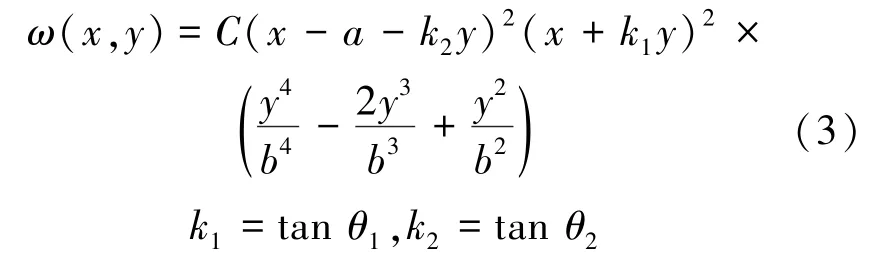
式中,C为待定系数;a为工作面滞后端推进长度;b为工作面垂直投影长度。
式(3)挠度函数不仅满足边界方程,还可变化出许多不同形式、满足不同类型板的边界条件:
(1) 当k1=k2≠0 时,薄板模型为等腰梯形板;
(2) 当k2=0,k1≠0 时,薄板模型为直角梯形板;
(3) 当a=0 时,薄板模型为任意三角形板。
当6106 外段伪斜工作面煤体采出后,采空区形成近似直角梯形顶板,如图3 所示,梯形斜边为工作面方向,工作面推进方向为x方向,梯形上下底边为工作面两端头推进距离。由于形成顶板力学结构的不同,不规则梯形采煤工作面顶板弯曲破断呈非对称形态。此时,θ2=0,θ1≠0,将挠度近似函数式(3)代入板的微分方程式(2)中,得
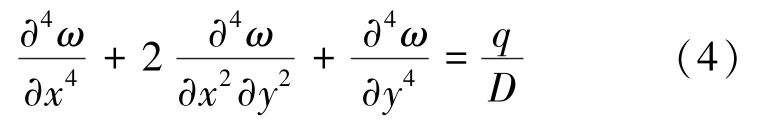
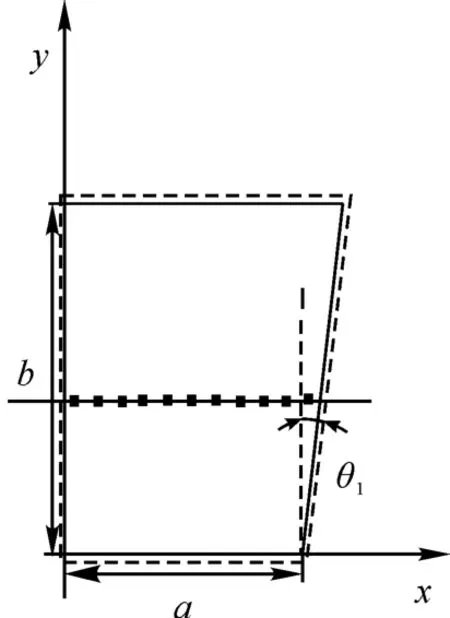
图3 直角梯形薄板模型Fig.3 Rectangular trapezoidal thin plate model
应用最小二乘配点法求待定系数C,为了提高计算精度,可先配线,然后再配点。
结合南阳坡煤矿6106 工作面(外段)参数,当初次来压时,k2=0,k1=0.091,模型为θ1=5.2°的直角梯形薄板(图3)。令a=45,b=110,在直线y=0.45b上配置11 个点,求得最小二乘配点法基本公式中的系数矩阵。

代入最小二乘配点法公式[16]:
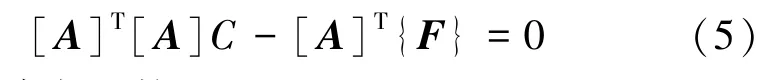
求得待定系数:
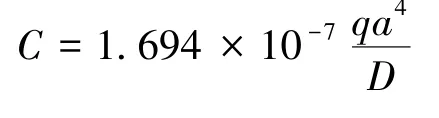
则板的挠度函数为
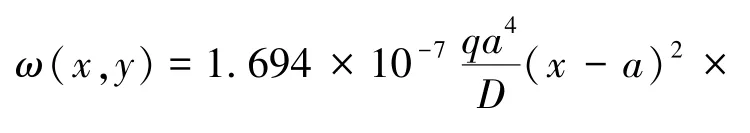

1.3 梯形基本顶板力学特性分析
根据弹性力学中对薄板横截面上的内力计算,板内弯矩的计算公式为
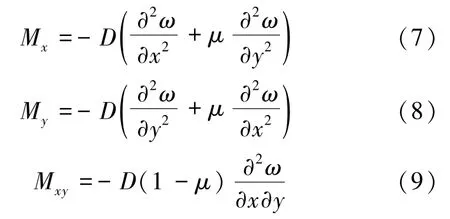
将得到的挠度函数关系式ω(x,y) 代入式(7)至式(9) 中,得到梯形板的弯矩分布函数:
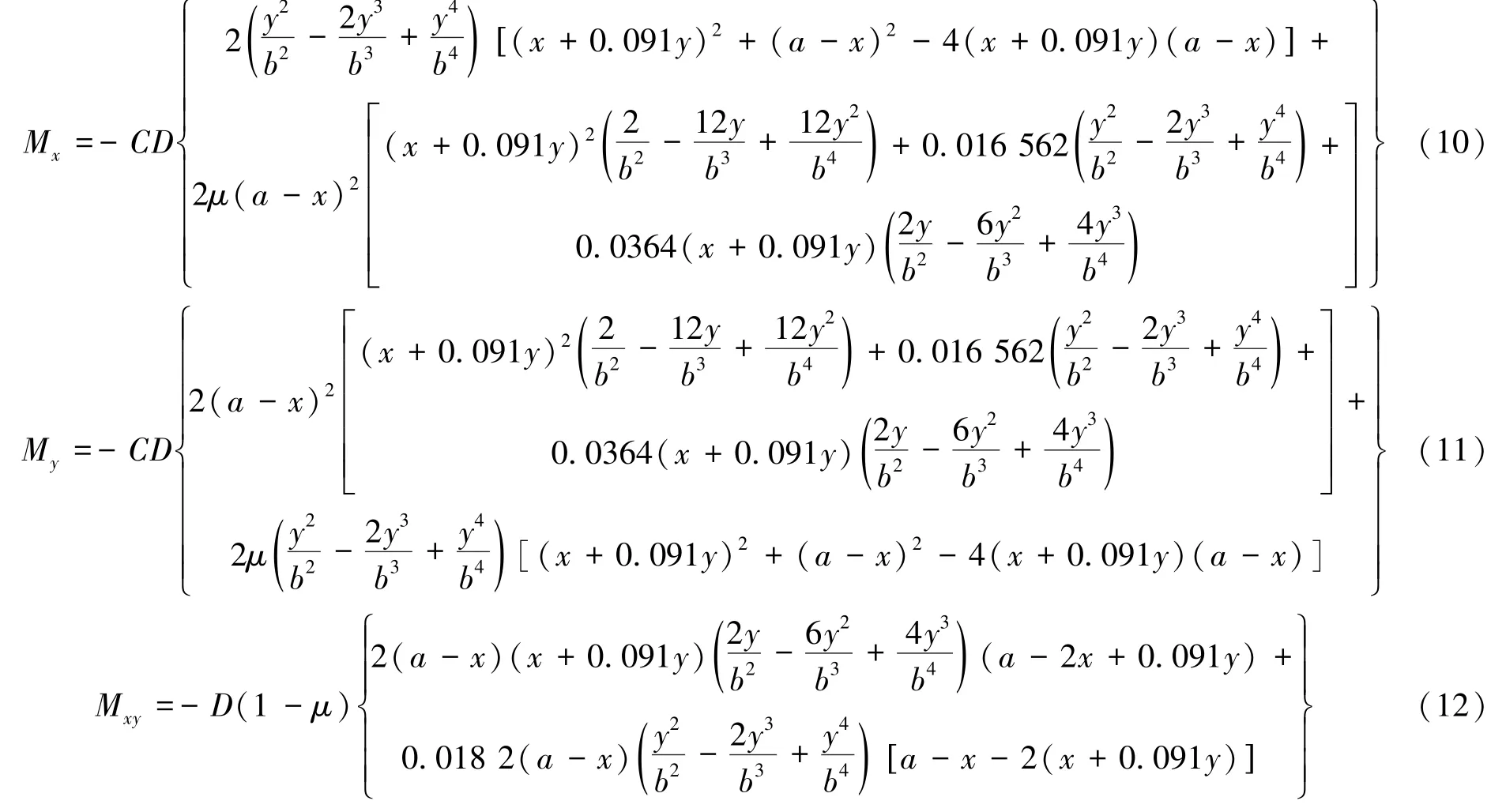
为分析均布荷载作用下四边固支直角梯形板的力学特性,取工作面滞后端推进长度45 m,工作面垂直投影长度110 m,工作面与滞后端巷道夹角为84.8°,则θ1=5.2°。设薄板厚度5 m,弹性模量25 GPa,泊松比0.3,体积力0.024 MN/m3,煤层埋深240 m,因此均布荷载为5.76×103 kN/m2。
梯形基本顶上任意单元体的弯矩分量Mx、My、Mxy三者的关系为

式中,M1、M3分别为最大、最小主弯矩。
梯形薄板任意截面上的最大拉应力σmax和该截面主弯矩M、抗弯截面系数W的关系为

由式(13)至式(15)可得,薄板主弯矩与最大拉应力成正比例关系,基本顶上、下表面对应点的主应力大小相等,方向相反;而上、下表面点的主应力与主弯矩成正比例关系。所以,可用主弯矩所在位置来确定基本顶的破断位置,即运用主弯矩来分析基本顶的内力以及可能发生破断的位置[17]。
利用Mathcad 数学分析软件求解运算式(10)至式(12),并代入式(13)和式(14)得到梯形薄板主弯矩的分布数据,再导出至Origin、Excel 等数据分析软件,然后绘制板内弯矩分布曲面图(图4)。
由图4 可知,梯形基本顶各个节点的最大、最小主弯矩M1、M3的分布规律如下:
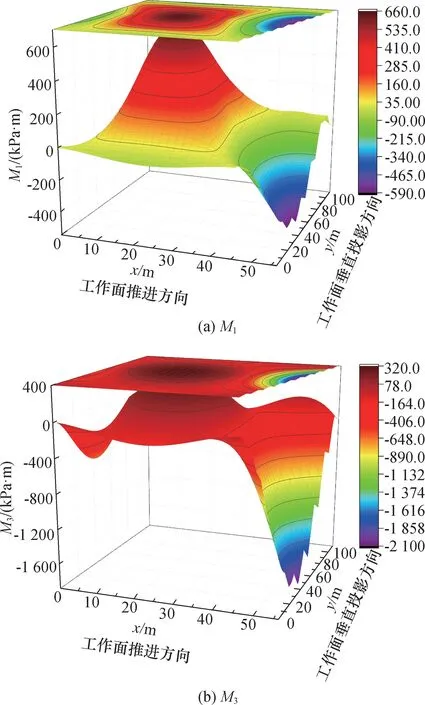
图4 直角梯形薄板内主弯矩分布Fig.4 Distribution of bending moment in angle trapezoidal thin plate
(1) 基本顶中部各个节点的最大、最小主弯矩均为正值,此区域基本顶上表面受压应力、下表面受拉应力;
(2) 基本顶四周边界最大、最小主弯矩均为负值,此区域基本顶上表面受拉应力、下表面受压应力;
(3) 四条边界中,斜边主弯矩极值最大,其次为直角长边,再次为超前推进一侧边界,滞后推进一侧边界主弯矩极值最小。
由于岩石材料的抗拉能力远远小于抗压能力,基本顶最易发生破坏的位置在中部的下表面与四边的上表面。
由式(13)、式(14)计算可得,在四边固支直角梯形板直角边(0,46 m)处和斜边(51 m,66 m)处主弯矩最大,分别为M1= -170.738 kPa·m,M3=-615.106 kPa·m 和M1=-589.942 kPa·m,M3=-2 094.592 kPa·m;在下底短边(22.5 m,0)处和上底短边(17 m,110 m)处主弯矩最大,分别为M1= -49.794 kPa·m,M3=-165.831 kPa·m 和M1= -111.135 kPa·m,M3=-370.449 kPa·m。在均布荷载作用下,四边固支直角梯形薄板的内力分布规律表明:从开切眼到煤壁工作面处,板内弯矩在数值大小上整体呈先升高再减小的趋势,开切眼与煤壁上方顶板弯矩为负,板中央弯矩为正;从巷道一端到另一端方向上,板内弯矩分布整体趋势与推进方向相似,但超前推进一侧顶板弯矩大于滞后一侧。
板内主弯矩分布在x方向上整体呈现近似的抛物线形状,如图5(a)所示。当y=55 m 时,板内弯矩呈开口向下的近似抛物线状,弯矩最大值处于中心偏左位置;在y方向上,当x=24 m 时,板内弯矩呈开口向下的近似抛物线状,弯矩最大值位于中心偏右。从两条曲线及图4 可以看出,直角梯形薄板中部主弯矩最大值位于板中心左上方位置,数值为正。

图5 不同方向下主弯矩分布规律Fig.5 Distribution law of principal bending moment in different directions
正的应力合成的主矢量为正,正的应力乘以正的矩臂合成的主矩为正,反之为负。因此,在梯形薄板的中部区域受到较大的压应力,可能发生压破坏;而四边近似中心位置出现较大拉应力,其中两长边拉应力更大,可能发生拉破坏。由于梯形薄板所受的拉应力和压应力在数值上相等、方向相反,且梯形薄板抗压不抗拉。因此在梯形薄板(0,46 m)和(51 m,66 m)处首先出现拉破坏,其次在两短边(22.5 m,0)和(17 m,110 m)处出现拉破坏,从而导致其余位置的失稳破坏。
1.4 基本顶破断规律及差异
本文结合矩形薄板的破断规律以及矩形薄板与直角梯形薄板的弯矩分布差异,推断直角梯形薄板的破断规律。如图6(a)所示,以推进长度45 m、工作面长度110 m 为例,在四边固支的矩形薄板中,四条边界上弯矩分布的最大值都处于边界的中心位置,而正弯矩的最大值则位于板的中央,因其弯矩分布的对称性,首先在长边的中心部位上表面出现断裂,而后在短边的中央形成裂缝,待四周裂缝贯通呈“O”形后,板中央的弯矩达到最大值,超过强度极限而形成裂缝,最后形成“X”型破坏。此时,在工作面两端形成对称及等大的“弧形三角块”。

图6 直角梯形与矩形薄板四边最大弯矩位置Fig.6 Position of maximum bending moment on four sides of rectangular trapezoid and rectangular thin plate
均布荷载作用下的直角梯形薄板弯矩分布规律与矩形薄板大致相似,不同之处在于,直角梯形薄板的直角长边上主弯矩最大值出现在中心位置偏向较短短边一侧,斜边上主弯矩最大值出现在中心位置偏向较长短边一侧,较长短边上主弯矩最大值出现在中心位置偏离直角长边一侧。相较于矩形薄板,直角梯形薄板四边的最大弯矩点整体略向逆时针方向移动,其中斜边主弯矩极值大于直角长边,较长的短边主弯矩极值大于另一短边。当θ1=5.2°时,直角梯形薄板四边主弯矩极值位置如图6(b)所示。
由图6 可知,直角梯形薄板与矩形薄板的破断规律最大不同在于,初始断裂位置的不同。在伪斜工作面中,因工作面一端滞后推进,使得工作面与巷道两端的夹角不同,在超前端一侧,顶板的破断位置更远离工作面。初次来压时,超前一侧顶板悬漏距离本就大于滞后一侧,因此超前一端“弧形三角块”大于滞后一端;周期来压时,根据主弯矩极值的分布位置规律,超前端“弧形三角块”也应大于滞后端。所以当工作面伪斜布置时,采空区顶板垮落后,“弧形三角块”的大小与一般工作面不同。
对于梯形采空区顶板,工作面推进快的一端将形成锐角约束,推进慢的一端将形成钝角约束。通常来讲,锐角区域邻近两实体煤帮对顶板的约束较直角区域强,同理直角区域较钝角区域强。但根据本文理论分析结果可得,伪斜工作面梯形基本顶在割煤方向上最大、最小主弯矩极值点均向超前端一侧移动,而在推进方向上超前端主弯矩极值点向后移动,因此超前端锐角约束强主要体现在推进方向上,而在工作面方向并未形成较强约束。
2 梯形顶板破断规律数值分析
2.1 模型建立
根据6016 外段工作面伪斜布置方式,结合表1建立模型尺寸250 m×400 m×35 m,共划分28 000 个单元。FLAC3D计算模型(图7)顶部为自由边界,其余各面均施加位移约束。模型采用摩尔-库伦本构模型,顶部施加均布荷载5.76×103kN/m2。分别计算直角梯形四条边界上的应力分布与极值位置,与常规矩形采空区边界应力分布进行比较,探究梯形采空区与矩形采空区顶板的破断位置及其规律的不同。
图7 数值模拟模型Fig.7 Numerical simulation model
2.2 模拟结果分析
模型开挖后,采空区呈直角梯形状,采空区顶板与煤岩体应力分布如图8 所示,并将直角梯形采空区的4 个边界点分别设为A、B、C和D。采空区四周煤壁内侧应力分布总体上分为增压区、减压区、极限平衡区。在直角梯形4 条边界线上,应力分布总体呈现开口向上的近似抛物线状。
在常规矩形采空区中,4 条边界线上应力极值都位于中心位置[18],而直角梯形采空区应力分布略有不同(图9)。图9 中x为工作面推进方向,y为工作面的垂直投影方向。图9(a)为直角梯形斜边应力分布曲线,结合图8 对4 个边界点的定义,以B点为坐标原点,斜边BC为横轴方向。斜边边界应力极值位于58 m,处于中心靠右侧,在梯形中靠近较长短边一侧。图9(b)为直角长边应力分布曲线,以A点为坐标原点,长边AD为横轴方向,应力极值位于51 m,处于中心靠左侧,在梯形中靠近较短短边一侧。图9(c)为较短短边应力分布曲线,以A点为原点,短边AB为横轴方向,应力极值位于24 m,处于中心靠右侧,在梯形中靠近斜边一侧。图9(d)为较长短边应力分布曲线,以D点为原点,短边DC为横轴方向,应力极值位于26 m,处于中心靠左侧,在梯形中靠近直角长边一侧。在4 条边界的各自2 个端点均出现了不同程度的应力集中,其中以推进方向上两条短边(梯形上底与下底)最为明显。

图8 采空区与煤岩体应力分布Fig.8 Goaf and stress distribution of coal and rock mass
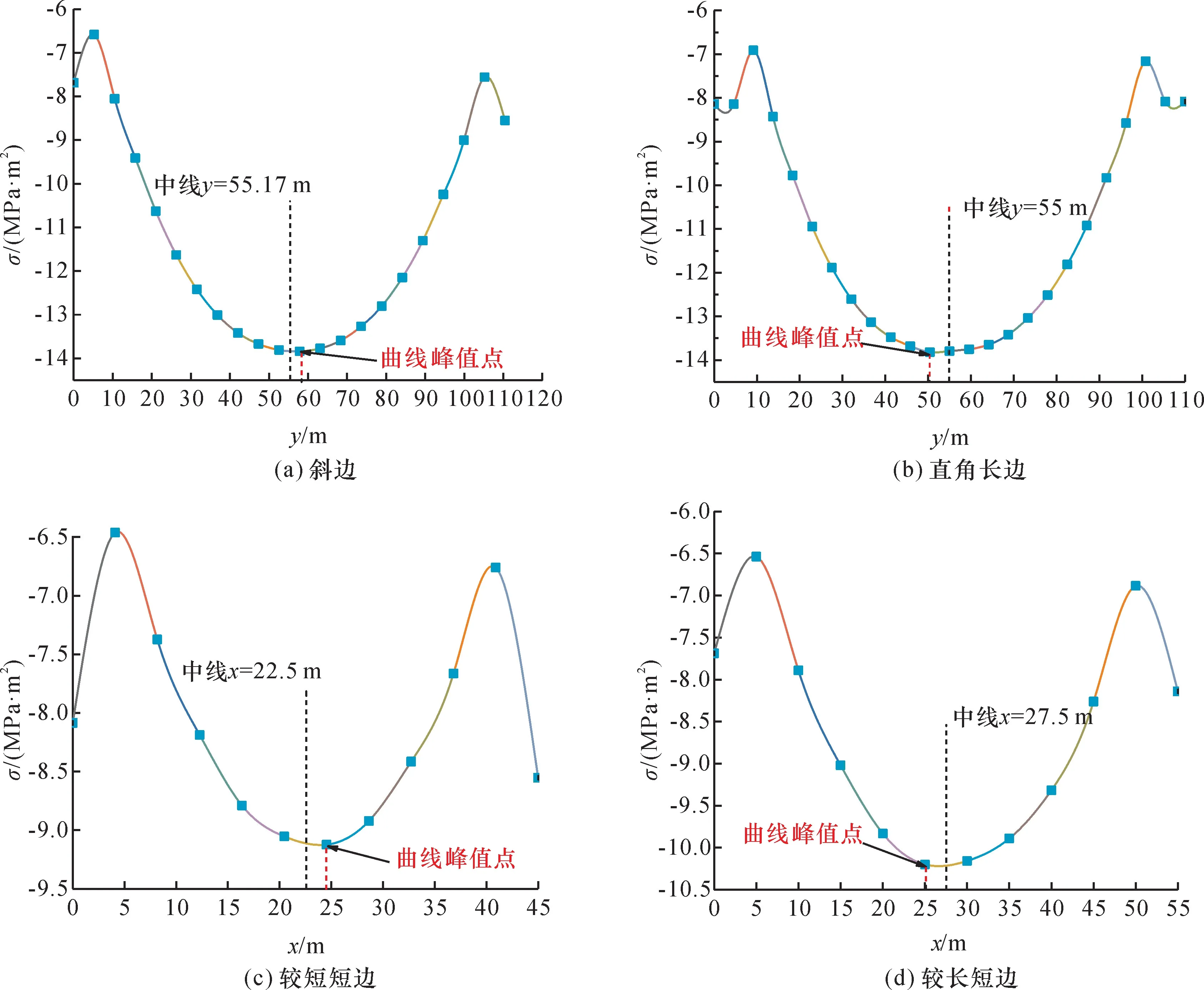
图9 直角梯形四条边界顶板应力分布曲线Fig.9 Four boundary stress distribution curves of right angle trapezoid
通过对直角梯形采空区的数值分析,确定直角梯形4 条边界上应力分布的极值位置,如图10 所示。梯形采空区顶板4 条边界线上的应力极值相较于矩形顶板来说,整体呈逆时针方向偏移。数值分析结果与理论计算结果相似:当工作面伪斜布置,顶板初次来压时为直角梯形状,顶板的破断首先发生在工作面靠近超前推进端的一侧与直角长边靠近较短短边的一侧,其次在较长短边中心靠近直角长边一侧与较短短边中心靠近斜边一侧。结合已有的矩形顶板初次来压规律与直角梯形顶板的弯矩、应力分布规律可得:伪斜工作面初次来压时,顶板破断为非传统“O-X”型,而是向逆时针方向旋转的椭圆状“O-X”型破断。

图10 直角梯形薄板首先破断点位置与O-X 型破断Fig.10 Position of initial breaking point and O-X shape of rectangular trapezoidal thin plate
3 现场验证
南阳坡煤矿6106 工作面外段与内段呈斜交状态,接替区域存在转角大于50°的扇形开采区域。为保证扇形区域的合理开采及工作面接替任务顺利进行,对6106 工作面(外段)运输巷一端进行超前推进处理,从而形成伪斜工作面。初始布置方式为进风巷端头超前距离10 m,初次来压时进风巷端头进尺为55 m,回风巷进尺为45 m,平均来压步距为50 m。
当梯形采空区基本顶初次来压后,两巷端头顶板并没有完全垮落,随着开采继续推进,在工作面进风巷端头顶板形成近30 m 的“弧形三角块”,无法及时自然垮落,南阳坡煤矿及时进行了强制垮落的处理方案,消除安全隐患。随着工作面继续向前推进,逐渐形成平行四边形采空区,当基本顶周期来压后,回风巷一侧初始断裂位置位于中心偏右,进风巷初始断裂位置位于中心偏左,因此在进风巷一侧形成的“弧形三角块”的面积大于回风巷一侧,如图11 所示。其中d1、d2右侧端点位于工作面推进端(较粗虚线与边界交点处),而左侧端点分别到达上次周期来压后主弯矩极值破断位置,由图分析可得d2<d1,即滞后端小于超前端。此时顶板的“O-X”破断形状呈顺时针椭圆状旋转。南阳坡煤矿超前端为梯形的下边界,而本文所做力学模型超前端为梯形上边界,因此“O-X”呈不同方向旋转,但整体规律相同。当超前端为梯形(或平行四边形)下边界时,顶板断裂线为顺时针旋转的椭圆状“O-X”型;当超前端为梯形(或平行四边形)上边界时,顶板断裂线为逆时针旋转的椭圆状“OX”型。
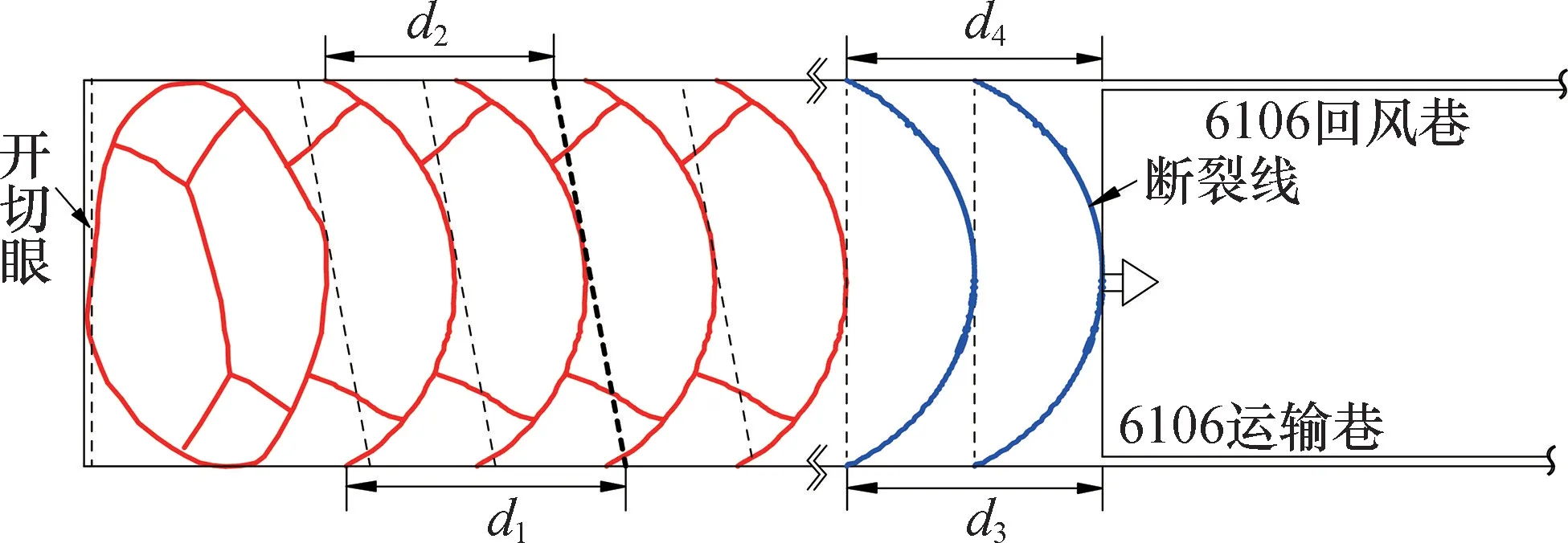
图11 基本顶垮落特征Fig.11 Characteristics of basic roof caving
6106 工作面(外段)回采结束后,经过巷道转角,工作面与巷道夹角恢复直角状态。此时工作面继续向前推进,将形成传统矩形采空区顶板,如图11 所示。由图11 看出,d3=d4,因此当工作面周期来压后,工作面两端头形成等大且对称的“弧形三角块”。
4 结 论
(1) 通过建立直角梯形薄板力学模型、对薄板进行理论计算,得到板内弯矩的计算公式,分析顶板弯矩的分布,得出初次破断的位置:超前一侧主弯矩最大值向后移动;滞后一侧主弯矩最大值向前移动;直角边最大主弯矩向滞后端移动;斜边主弯矩向超前端移动。
(2) 采用数值模拟的方法对直角梯形顶板的应力分布进行求解。结果显示,四边应力最大值点的位置与理论计算结果一致:超前一侧最大值点向后移动;滞后一侧向前移动;直角边最大值点向滞后端移动;斜边最大值点向超前端移动。根据基本顶岩板结构破断准则,数值分析结果与理论计算所得规律一致,得到验证。
(3) 锐角区域邻近两实体煤帮对顶板的约束较直角区域强,同理直角区域较钝角区域强。锐角区域较强约束效果主要体现在推进方向上,而在工作面方向上并未产生较强约束。
