次分数布朗运动下具有随机利率和跳跃风险的两值期权定价

程潘红，许志宏

（1.上海理工大学 管理学院，上海200093；2.滁州学院 数学与金融学院，安徽 滁州239000；3.日照职业技术学院 公共教学部，山东 日照276826）

期权作为典型的金融衍生品（远期、期货、互换、期权）之一，具有悠久的发展历史。现代意义上的期权是从1973 年美国芝加哥期权交易所推出16 只股票组成的股票期权开始的［1］。合理的期权价格是双方交易的前提，是投资者进行套期保值、获取收益的有力保障，且对完善期权定价理论体系有着极其重要的意义。因此，期权定价研究一直是金融工程学的核心课题。

两值期权是合约条款变化产生的一种新型期权。它是构成复杂期权的基本工具。Thavaneswaran 等［2］和Miyake 等［3］探讨了模糊环境下两值期权的定价问题。孙天宇等［4］研究了布朗运动下有交易成本和红利的两值期权定价，利用无风险套利原理和偏微分方程方法计算得到不同类型的两值期权价格表达式。袁国军［5］研究了基于半离散化CEV 过程的两值期权定价，给出期权价格的差分格式。这些关于两值期权的定价研究都是在金融资产的价格波动相互独立，且对数收益率服从正态分布的前提下进行的。然而，大量实证研究表明，金融资产的价格波动是有偏的随机游走，具有明显的自相似性和长记忆性。由于分数布朗运动（fractional Brownian motion，FBM）刚好具有自相似性和长记忆性等特点，因此可以应用FBM 刻画金融资产价格的随机波动特征。2015 年，潘坚等［6］对分数维B-S 期权定价公式进行了推广与改进，提出了分数维Hull-White 利率模型下的欧式期权定价模型，利用风险中性原理和偏微分方程方法求解得到相应的期权定价公式。2018 年，韦才敏等［7］考虑了有交易成本和红利支付时分数布朗运动环境下的两值期权定价，应用偏微分方程方法求解得到相应的两值期权定价公式。2020 年，刘翩等［8］考虑到股票价格波动面临的跳跃风险，构建了分数Hull-White 利率下标的资产服从分数跳-扩散过程的欧式期权定价模型，应用分数布朗运动性质与偏微分方程方法推导得到欧式期权的定价公式。

尽管分数布朗运动具有自相似性和长记忆性等特点，但Rogers［9］和Cheridito［10］研究发现分数布朗运动应用于金融市场时存在套利机会。Björk 等［11］研究表明在Wick 自融资策略下得到的期权定价模型不具有经济意义，基于Wick 积分的分数布朗运动应用于金融市场时受到限制。为解决这些问题，并考虑到金融资产价格过程的长记忆性，可以采用比分数布朗运动更一般的高斯过程（混合分数布朗运动、次分数布朗运动等）来刻画金融资产价格变化的行为模式。如康莉等［12］研究了混合分数布朗运动环境下具有跳跃风险的两值期权定价，运用不同方法得到期权价格的解析解与数值解。虽然采用混合分数布朗运动刻画金融资产价格的随机波动比经典的布朗运动有所改进，但金融资产价格的增量是平稳的。然而，在实际的证券市场中金融资产价格的增量和时间始末有着密切的关系，因此一些学者采用次分数布朗运动（sub-fractional Brownian motion，SFBM ）刻画金融资产价格变化的行为特征。2004 年Bojdecki 等［13］首次提出SFBM 的概念，并指出SFBM 不仅保持了FBM 的自相似性、长记忆性等性质，而且具有比FBM 更快的退化速度以及增量非平稳性。肖炜麟等［14］构建了SFBM 下带交易费用的备兑权证定价模型，并通过实证分析说明了SFBM 下有交易费用定价模型的合理性。叶芳琴等［15］利用随机分析理论和次分数Itô公式，提出了SFBM下支付红利的两值期权定价模型，并运用偏微分方程方法计算得到两值期权价格的闭式解。

回顾国内外文献发现，已有关于两值期权的定价研究大多专注于探讨采用适合的数学模型刻画股票价格的随机波动特征，极少有综合考虑股票价格的长记忆性和跳跃风险、利率的随机性、利率同股票价格的相关性对两值期权展开研究。受已有研究成果的启发，本文采用次分数布朗运动刻画股票价格的随机波动，将利率的随机性、长记忆性以及股票价格会由于突发事件的发生而引起的不平常跳跃，同时考虑到两值期权定价模型的构建中，提出次分数Vasciek 利率模型下具有跳跃风险的两值期权定价模型。运用次分数布朗运动的Itô公式、保险精算方法计算两值期权的定价公式。最后通过数值模拟讨论相关参数对期权价格的影响，同时给出相应的经济意义。

1 预备知识与主要引理

1.1 两值期权定义

两值期权也称为数字期权、固定收益期权。两值看涨期权一般分为两种类型［16］：

（1）资产或无值看涨期权（asset-or-nothing call，AONC）：到期日T 时，如果标的资产价格ST大于执行价格K，则该期权支付一个等于资产价格本身的金额ST；如果低于执行价格K，则该期权没有价值。

（2）现金或无值看涨期权（cash-or-nothing call，CONC）：到期日T 时，如果标的资产价格ST大于执行价格K，则该期权支付一个固定的金额M；如果低于执行价格K，则该期权价值为零。

在到期日T 时，两值看涨期权的价值为

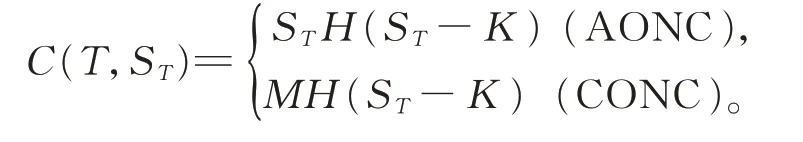
这里H ( x ) 是Heviside 函数。当x ≥0 时，H ( x )＝1；当x ＜0 时，H ( x )＝0。

类似地，在到期日T 时，两值看跌期权的价值为

1.2 次分数布朗运动

关于次分数布朗运动的更多性质可参阅文献［13，17－20］。

1.3 保险精算定价法

1.4 主要引理

2 金融市场模型

2.1 模型假设

设(Ω，F，P) 是一概率空间，{ξHt}t＞0是该概率空间上的次分数布朗运动。现对金融市场做如下假设：

（1）不存在交易费用及交易税；

（2）市场上存在两种资产：一种为无风险资产，其短期利率rt是随机波动的。采用次分数Vasicek 利率模型刻画利率期限结构动态变化的特征，即rt满足

其中：α，β，σr均为正常数，分别表示均值回复速率、长期均衡利率和短期利率的波动率；ξH1(t) 是H∈(1/2，1 ) 的次分数布朗运动。

另一种资产为两值期权，其对应的标的资产价格St满足如下带跳的扩散过程：

2.2 次分数Vasicek 利率模型下两值期权的定价公式

2.2.1 资产或无值期权的定价公式

定理1在利率rt满足次分数Vasicek 模型、股票价格St服从几何次分数布朗运动的条件下，到期日为T、执行价格为K 的资产或无值看涨期权（AONC）在t ＝0 时的价值为

类似于定理1 的推理过程，容易证明定理2 成立。

由于现金或无值看跌期权的到期收益为VAONP＝MH ( X － ST)，因此，类似定理2 的证明，容易得到CONP 在t ＝0 时的价值为

3 数值分析

为了评价模型的性能，本文通过一些数值算例进行了如下研究：一是比较分析次分数布朗运动环境下随机利率与常数利率这两种情形的两值期权定价结果；二是研究跳跃风险对期权定价结果的影响；三是探讨两值期权价格关于相关参数的变化情况。由于篇幅有限，这里仅以资产或无值看涨期权（AONC）为例进行数值分析，数例中参数的基本取值如表1 所示。对于其他类型的两值期权，可做类似讨论。

表1 ANOC 定价模型中相关参数的取值情况Tab.1 Parameter value selection in ANOC pricing model

3.1 利率风险对AONC 价格的影响

受国家经济政策、股票市场状况等因素的影响，市场利率会出现较大的波动。因此，实际上利率是时刻变化的。为了考察随机利率对ANOC 价格的影响，根据定理1 和推论1，对ANOC 在Vasciek 利率与常数利率下的定价结果进行了比较分析，结果如图1 所示。

由图1 可知，随机利率下ANOC 价值高于常数利率下的ANOC 价值，并且随着到期时间的增大，两种情形下ANOC 定价结果的差异在逐渐变大。这说明利率的随机性是定价ANOC 时不可忽略的因素。

图1 ANOC 的期限结构Fig.1 Term structure of ANOC

3.2 跳跃风险对ANOC 价格的影响

在金融资产交易的过程中，由于突发事件（自然灾害、疾病、战争、金融危机等）、市场新信息的发布及政策变化都可能使得金融资产价格发生不平常的跳跃，因此探讨ANOC 在纯扩散过程和具有跳跃风险这两种情形下的定价区别，如图2 所示。

由图2 可知，当标的资产价格受到突发事件影响而发生跳跃，并且在假设跳跃幅度的期望值为正值的情况下，ANOC 价值高于纯扩散过程下的期权价值，这与实际情况相符。两者的显著差别说明了将跳跃风险考虑到ANOC 定价模型的构建中是非常有必要的。此外，观察图2 还可以发现，ANOC 价值随着S0的增大而增大，这源于S0越大，则标的资产在到期日的价格高于执行价格的可能性就越大，即期权的内在价值越大。

图2 不同定价模型下的ANOC 价值图Fig.2 ANOC value under different pricing models

3.3 SFBM 模型中相关参数对AONC 价格的影响

本节的数值分析通过改变ANOC 定价模型中的一些参数值，说明其对ANOC 价值的影响，而其他参数的取值参见表1。

图3 描述了ANOC 价值关于执行价格K、短期利率的长期均值β及赫斯特指数H的变化情况。从图3（a）发现，ANOC 价值随着K的增加而降低，即ANOC 价值是K的减函数。这与现有文献的结论一致，也与实际情况相符。图3（b）直观地呈现了ANOC价值与β之间的正相关关系。这源于随着β的增大，随机利率也随之增大，较高的利率提高了ANOC 价值。图3（c）为ANOC 价值关于H的变化图像。 可以看出，随着H的增加，ANOC 价值随之上升，即ANOC 价值随着股票价格长程相关性和利率长程相关性的增强而升高。

图3 ANOC 价值关于相关参数的变化情况Fig.3 ANOC value against correlated parameters

4 结论

在考虑金融资产价格具有长记忆性、跳跃风险以及利率具有随机性的情况下，本文围绕两值期权定价问题，提出次分数跳-扩散过程下具有随机利率的期权定价模型，运用次分数Itô公式、性质和保险精算方法推导得到两值期权的定价公式，改进了以往的经典定价模型。最后，通过数值算例对资产或无值看涨期权（ANOC）受利率、跳跃风险、标的资产初始价格、执行价格、短期利率的长期均值以及赫斯特指数等因素影响而发生的变动情况进行了详细的分析。结果显示：（1）利率的随机性会影响ANOC 的定价，此时的定价结果高于常数利率情形下定价结果，且随着短期利率长期均值的增加，ANOC 价值会随之增加；（2）在跳跃幅度的均值为正值的假定下，跳跃风险的存在增加了ANOC 价值，符合实际情况，这表明定价ANOC 时考虑跳跃风险是非常有必要的；（3）ANOC 价值随着标的资产初始价格、赫斯特指数的增大而增大，随着执行价格的增大而减小。

针对本文提出的两值期权定价模型，可以将交易对手违约风险、金融资产价格波动率的时变性等因素考虑到定价模型的构建中。此外，进一步就定价模型开展参数估计研究，并结合期权市场现实情况进行实证分析，比较不同定价模型下的定价结果，选出更为贴近市场的定价模型。