非线性方程组的修正共轭梯度法及其应用

李丹丹，李远飞

（广州华商学院 数据科学学院，广东 广州511300）

0 引言

考虑如下非线性单调方程组

其中θ：Rn→Rn是连续可微函数且单调，即θ(x)－θ(y)，x－y≥0，∀x，y∈Rn。

非线性单调方程组可广泛运用于压缩感知中的信号恢复、图像处理、经济等跨学科领域［1－3］。若干具有快速局部收敛性质的迭代算法可高效求解问题（1），如牛顿法、拟牛顿法和LM 算法等［4］。上述算法需计算和存储矩阵信息，不适用于求解大规模非线性单调方程组问题。共轭梯度法［5－6］因算法结构简单、易操作、储存量小等优点被推广到求解大规模非线性方程组，并验证了其优良性质。

式（3）中βk为共轭参数，θ(xk) 简写为θk，而搜索方向dk与线搜索方法决定了共轭梯度法的优劣性，且在一定的程度上体现算法收敛效果。

Wei 等［7］给出了一个修正HS 算法，其共轭参数为

其中yk－1＝θk－θk－1。Sun 等［8］提出了一个杂交共轭梯度投影方法，该方法的搜索方向具有良好的信赖域特性，其中共轭参数为

其中μ ＞1，yk－1＝θk－ θk－1。基于Wei 等［7］和Sun 等［8］的良好性质，受此启发，本文设计出一个新的修正搜索方向，其共轭参数为

本文借鉴Wei 等［7］的修正HS 算法与Sun 等［8］的杂交共轭梯度投影算法思想，设计出一个新的搜索方向，再结合Dai 等［11］的线搜索方法和Solodov 等［12］经典的超平面投影技术，提出了一个无导数型的修正共轭梯度算法。新算法的搜索方向满足充分下降性和信赖域特性，保证了算法的有效性。在适当的假设下，证明了新算法的全局收敛性。此外，在数值试验中，利用新算法求解非线性正规方程组和稀疏信号重构问题，结果阐明了新算法的高效性、可行性及实用性。

1 算法描述

建立求解非线性单调方程组问题（1）的修正共轭梯度算法（MHSN）：

2 充分下降性和信赖域特性

证明算法MHSN 具有充分下降性和信赖域特性，这为分析算法的全局收敛性起到积极的作用。

引理1由式（3）和式（4）所确定的搜索方向dk满足以下性质：

3 全局收敛性分析

本节分析算法MHSN 的全局收敛性质，需作假设B：

（B1）非线性单调方程组问题（1）的解集非空；

（B2）函数θ (x) 在Rn上是Lipschitz 连续的，即存在常数L ＞0，有

下面给出算法MHSN 的适定性引理，即证明算法是有意义的。

引理2在假设B 条件下，算法MHSN 是有意义的。

4 数值试验

4.1 非线性正规方程组

在算法MHSN 的步骤2 中，采用Fang［14］中算法MRMIL3 产生搜索方向dk，其余步骤与算法MHSN一致，得到的算法记为算法MRMIL3。

相关参数：β＝1，ρ＝0.5，σ＝0.096，μ＝1.81。

运行环境：采用MATLAB（2014a）实现，Windows10（64 bite），RAM：8 GB，CPU：3.60 GHz。

终止准则：‖θk‖≤10－5，迭代次数上限为1 000，维数为［4 500，12 000，24 000，30 000，45 000］。

测试问题共10 个［10，15－17］，数值结果如表1 所示，其中Pro 为问题序号，Dim 为维数，Iter 为迭代次数，NF为函数计算次数，Time 为程序运行时间（单位：秒）。

表1 各类算法数值结果Tab.1 Numerical results of various methods

续表1 各类算法数值结果Continued Tab.1 Numerical results of various methods

为了更直观反映三种算法的性能指标（迭代次数、函数计算次数和运行时间），采用Dolan［18］的评价方式，描绘了迭代次数性能图、函数计算次数性能图和运行时间性能图，如图1 至图3。

图1 迭代次数性能图Fig.1 Performance profiles of iterations

图2 目标函数计算次数性能图Fig.2 Performance profiles of the number of objective function

图3 运行时间性能图Fig.3 Performance profiles of CPU time

从表1 可知，算法MHSN 和算法MRMIL3 都在有限迭代次数内成功求解非线性正规方程组。同时，在同等条件下，数值结果表1 说明了算法LCGP 总体上比算法M3TFR 更优，各类指标数值更少。性能图1－3 显示算法MHSN 总体上比算法MRMIL3 更好，具有更好的鲁棒性，故验证了算法MHSN 是有效的且适合于求解大规模非线性单调方程组。

4.2 稀疏信号重构问题

本小节主要考虑压缩感知中的稀疏信号重构问题［19］。使用算法MHSN 和算法MRMIL3 求解稀疏信号恢复问题。

在测试中，信号的相关参数为n＝212，k＝210，原始信号只包含27个随机非零元素，其余为0。 此外，观测值y＝Bx͂＋η是带有噪声的高斯分布，其中x͂为原始信号B的随机高斯分布矩阵，η是均值为0 和方差为10－4的高斯噪声。采用均方误差（MSE）作为恢复信号的评判标准，即其中x*为恢复信号。程序终止准则为

由于观察值含有随机噪声，将程序运行10 次，其结果如表2 所示，显然，从运行时间和迭代次数的角度来看，算法MHSN 比算法MRMIL3 效率更高。

表2 稀疏信号恢复结果Tab.2 Results of sparse signal recovery

图4 为算法MHSN 和算法MRMIL3 在处理稀疏信号恢复的对比图，在图4 中由上到下分别表示为原始信号、观测值、由算法MHSN 和MRMIL3 恢复的信号。图5 为两种算法效果对比图，其中MSE 表示均方误差值，Iterations 表示迭代次数，CPU time 表示运行时间。

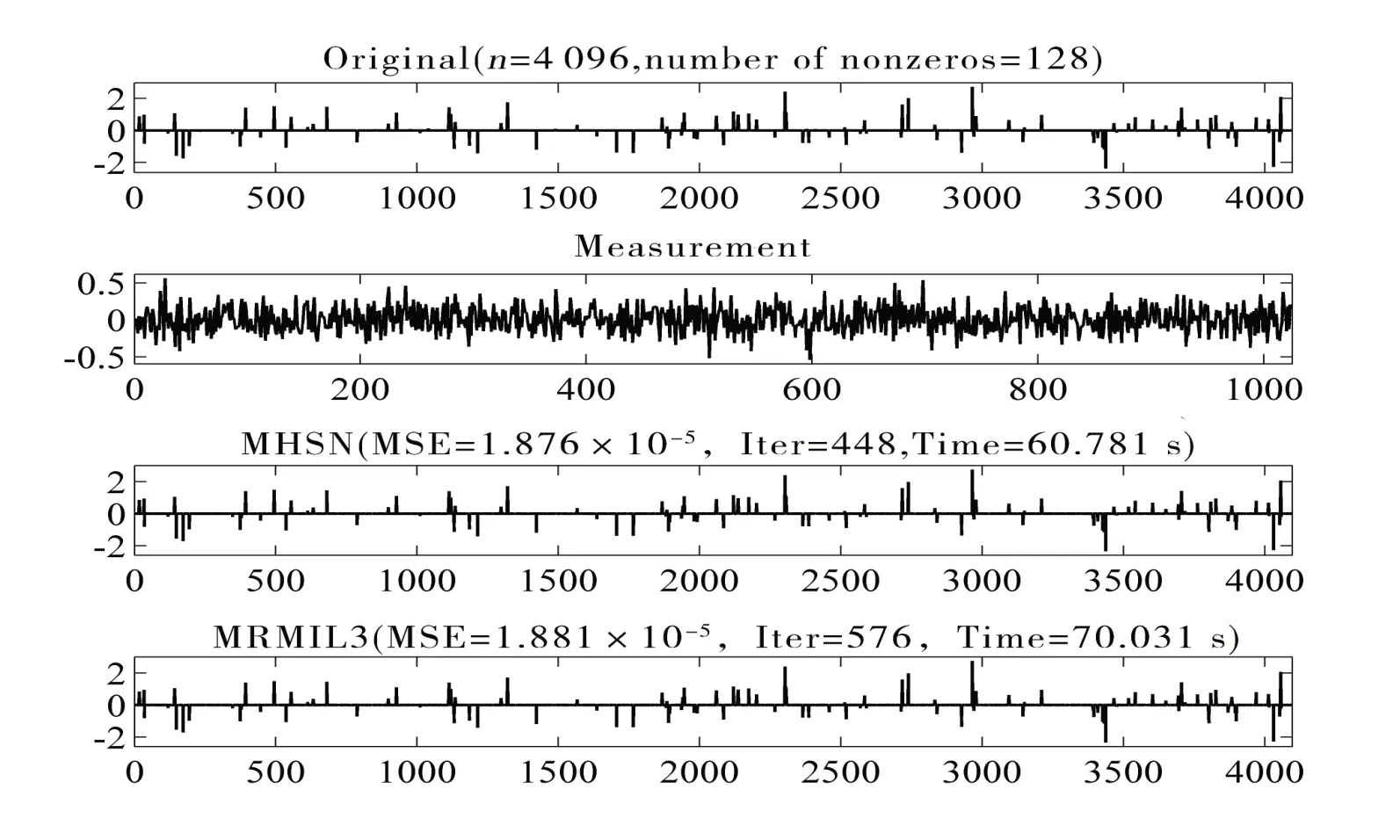
图4 稀疏信号恢复对比图Fig.4 Comparison of the sparse signal recovery

图5 算法MHSN 和算法MRMIL3 的比较结果Fig.5 Comparison of the MHSN and MRMIL3 algorithms

从图4 可知，算法MHSN 和算法MRMIL3 都成功地恢复信号。由图5 可知，从迭代次数和运行时间来看，两种算法的均方误差都收敛于0，且算法MHSN 效果更好。从而验证了新算法具有实际应用价值。

5 结论

本文在杂交共轭梯度投影方法和修正HS 算法的基础上，设计出一个新的修正搜索方向，结合经典投影方法和最新的线搜索方法，提出了一个新的修正共轭梯度投影算法。证明了新算法具有优良的理论性质，通过对非线性正规方程组和稀疏信号重构问题进行求解，验证了新算法的有效性与实用性。同时还可将新算法推广到图像恢复问题的应用中。