2020年全国Ⅰ卷圆锥曲线解答题的拓展探究与教学启示*

广东省佛山市顺德区容山中学(528303) 贾中伟

云南省云南师范大学信息学院(650503) 唐明超

广东省佛山市顺德区容山中学(528303) 潘敬贞

1 试题呈现

(2020年课标全国Ⅰ卷理科第20 题)已知A,B分别为椭圆E:+y2= 1(a ＞1)的左、右顶点,G为E的上顶点,= 8,P为直线x= 6 上的动点,PA与E的另一交点为C,PB与E的另一交点为D.

(1)求E的方程;

(2)证明:直线CD过定点.

该题以椭圆为背景,结合向量数量积的坐标运算给出一个确定的椭圆,研究定直线上的动点与长轴两端点的连线与椭圆的两个交点所确定的直线的性质.试题呈现方式较常规,符合课标要求,是学生较为熟悉的定点问题.重点考查学生的数学运算,逻辑推理与数学建模等核心素养,文理同题亦体现了试题的命制紧扣新高考改革的方向.

2 试题解析

(1)由已知可得:A(-a,0),B(a,0),G(0,1),即可求得=a2-1,结合已知条件可得a2= 9,所以E的方程为+y2=1.

(2)设P(6,y0),可得直线AP的方程为:y=联立直线AP的方程与椭圆方程可得:整理得(y20+9)x2+6y20x+9y20-81 = 0,所以x1x2=由x1=-3 得x2=从而y2=所以点C的坐标为同理可得点D的坐标为所以,直线CD的方程为:

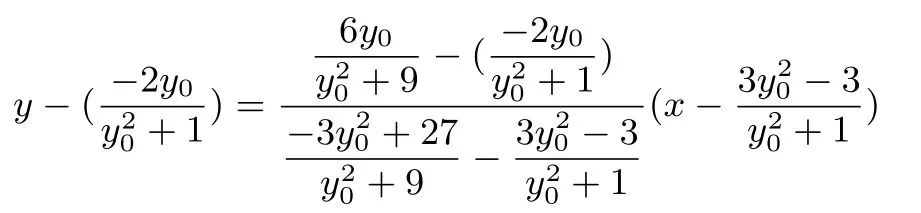
整理可得:

化简得:y=故直线CD过定点

试题的解答过程突出通法常法,还原解析几何最本质的特征即用代数运算研究几何性质,以求解直线与曲线的交点坐标为突破口,进而得出直线方程,再基于直线方程的特点得出直线的位置关系.试题整体上思维难度不大,具有鲜明的起点低、入口宽等特点,第(2)题要解决的问题目标明确,重点考查数学运算的基本方法与能力.

3 问题提出

问题1:该题呈现的是一个具体的椭圆和一条确定的直线,如果将椭圆一般化即给出的椭圆是任意的椭圆(文章为了讨论方便,默认椭圆均为焦点在x轴上的椭圆),直线CD还能过定点吗?

问题2:如果既将椭圆一般化,也将直线一般化为垂直于x轴的任意直线x=m(m /= 0),此时直线CD还能过定点吗?

问题3:逆向思考,已知直线CD过定点(m,0),与椭圆分别交于点C、D,记A、B分别为椭圆的左右顶点,设AC与BD相交于点P,动点P的轨迹是一条垂直于x轴的直线吗?

4 问题探究

4.1 探究问题1

题设1:已知A、B分别为椭圆的左、右顶点,P为直线x=6 上的动点,PA与E的另一交点为C,PB与E的另一交点为D;证明直线CD过定点.

证明:设P(6,y0),可得直线AP的方程为:y=联立方程可得:整理得[b2(a+6)2+a2y20]x2+2a3y20x+a4y20-a2b2(a+6)2=0,所以x1x2=又因为x1=-a,所以另一个根x2=从而y2=所以点C的坐标为同理可得点D的坐标为由两点式求直线CD的方程为:y=故直线CD过定点

从问题1 的探究过程可以看出代数运算较为复杂,但是最终推理结果却相对简洁.结合几何画板动态演示发现动直线CD确实经过位于x轴上的一个定点,说明该问题具有一般性.观察问题1 的结论发现定点横坐标为x=恰好包含了椭圆方程的基本元素a2与定直线方程x=6,不能排除这是巧合,但是亦有可能说明定点确实只与a2及定直线方程有关.可以猜想在一般情况下,给定直线x=m(m /= 0)时,直线CD的定点坐标为

4.2 探究问题2

由于计算过程较复杂,可以借助几何画板动态演示,发现猜想成立,从而可以得出结论1 如下.

结论1:已知A、B分别为椭圆E:=1(a ＞1)的左、右顶点,P为直线x=m上的动点,PA与E的另一交点为C,PB与E的另一交点为D,则直线CD过定点

4.3 探究问题3

借助几何画板动态演示后发现问题3 的猜想成立,从而可以得出结论2 如下.

结论2:已知A、B分别为椭圆E:=1(a ＞1)的左、右顶点,点M(m,0)是椭圆长轴上异于左右端点的任意一点,过点M(m,0)的动直线交椭圆于C、D两点,则动直线AC与BD交点P的轨迹是直线x=

5 问题的推广

基于以上3 个问题的探究过程,可以大胆猜想当AB是椭圆上过定点(m,0)的一条动弦时,相交弦AB与CD的端点连线AC与BD的交点P的轨迹也是一条定直线,且方程为x=结合几何画板动态演示发现猜想成立,从而可以得出结论3 如下.

结论3:如果A、B是椭圆上的任意两点,C、D也是椭圆上的任意两点,且线段AB与CD相交于点M(m,0),则称线段AB与CD是交点在长轴上的两条相交弦,那么动直线AC与BD交点P的轨迹是直线x=

6 问题的进一步推广

既然椭圆有如此优美的性质,那么双曲线会不会也有类似的性质呢? 按照从特殊到一般的思路探究双曲线中的情况,先对试题进行简单变式得到问题4,接着在问题4 的基础上借助几何画板动态演示进行推广.

6.1 问题4 推广

问题4:已知A、B分别为双曲线E:-y2= 1 的左、右顶点,P为直线x=6 上的动点,PA与E的另一交点为C,PB与E的另一交点为D.证明:直线CD过定点.

解析:设P(6,y0),可得直线AP的方程为:y=(x+3),联立直线AP的方程与椭圆方程可得:整理得(y20-9)x2+ 6y20x+ 9y20+81 = 0,所以x1x2=因为x1=-3 得x2=从而y2=所以点C的坐标为同理可得点D的坐标为所以,直线CD的方程为:

整理可得:

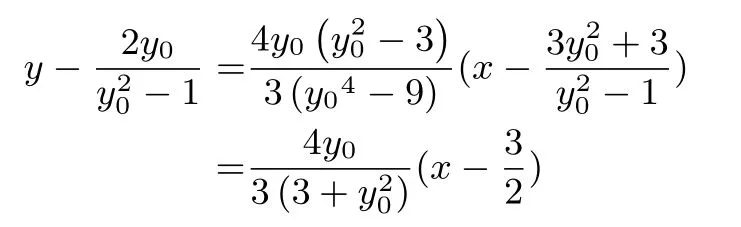
故直线CD过定点

从问题4 的解答过程中发现直线CD过定点而且不应该只是巧合,所以大胆猜想结论1 与结论2对双曲线也成立.进一步利用几何画板检验结论3 对双曲线也一样成立.

6.1 推广到抛物线

通过以上的探究发现椭圆与双曲线具有相同的性质,接下来探究抛物线中的情况.由于抛物线是非闭合曲线,只有一个顶点,可以从最特殊的情况着手探究.

问题5:已知抛物线E的方程为y2=4x,过焦点且垂直于x轴的直线与抛物线交于A,B两点,点P是准线上的任意一点,延长AP交抛物线于点C,延长BP交抛物线于点D,求直线CD与直线AB的交点坐标.

解析:依题意知A(1,-2),B(1,2),设P(-1,1),则lP A:y=联立直线lP A与抛物线E,解得; 联立直线lP B与抛物线E,解得D(9,6); 所以lCD:y=联立lAB与lCD得解得交点坐标为(1,0).

问题6:已知抛物线E的方程为y2= 4x,过点(2,0)的两条相交弦所在直线方程分别为lAB:y=x -2,lCD:y=-x+2,其中A，B，C，D 为相交弦与抛物线的交点，点A,C均在第一象限,求直线AC与BD的交点P的坐标.

解析:联立直线lAB与抛物线E,解得同理可得所以lAC:y=联立lAC与lBD解得交点坐标为P(-2,0),即交点P(-2,0)在直线x=-2 上.

从问题5 的解答过程可以看出当定直线为x=-1 时,过定点F(1,0)的弦与抛物线交于A,B两点,连接PA交抛物线于点C,连接PB交抛物线于点D,则直线CD也过定点F(1,0).从问题6 的解答过程中可以看出,过定点(2,0)的两条相交弦分别交抛物线于A,B,C,D四点,且直线AC与BD相交于定直线x=-2 上一点x=-m.

由于代数运算推理非常复杂,仍然选择使用几何画板进行演示验证,猜想成立,得出结论4 如下.

结论4:过抛物线对称轴上任意一定点M(m,0) 的两条弦分别为AB与CD,则同侧两端点所在直线AC与BD的交点P的轨迹是一条定直线x=-m.反之,连接定直线x=-m上任意一点P与抛物线的任意弦AB的两个端点,直线PA,PB分别交抛物线于C,D两点,则弦AB与弦CD有公共点M(m,0).

文中前后给出了四个结论,其中结论1、结论2 与结论3的本质都是一样的,反映的是椭圆或双曲线中两条相交弦端点所在直线的交点轨迹是一条垂直于对称轴的直线,而且直线方程与两条相交弦的交点坐标有着密切联系,即直线方程与交点横坐标的乘积为定值a2.结论3 是结论1 与结论2 的加强.结论4 反映了同一个问题背景在抛物线,椭圆和双曲线中所呈现的情况是不一样的,在抛物线中相交弦的交点横坐标与定直线方程的和为定值0.总之,由试题引出的四个结论是圆锥曲线焦点弦问题中的瑰宝,同时也体现了命题者的高超技艺与渊博学识,试题看似平淡无奇,实则内涵丰富,可以对其进行深入挖掘和拓展学习.

7 教学启示

7.1 理解《课标》,明确方向

《课标》是教学与考试的依据,教学过程是将课程标准相关要求进行分解完成的过程,考试是对课程标准规定的学习任务及学习目标完成情况的检测与评价.量变的积累是发生质变的必要过程,考试的成绩是教学过程中所有活动经验的集中体现,所以抓实过程,夯实基础,在落实“四基”与“四能”上下功夫很重要.课标明确要求学生在学习解析几何专题的过程中认识直线、圆、椭圆、抛物线、双曲线的几何特征,能建立它们的标准方程,会运用代数方法进一步认识并研究圆锥曲线的性质以及它们的位置关系.所以该部分的基础知识是要能熟练掌握曲线的标准方程及其简单性质;基本技能是要能在建系的基础上用代数运算描述曲线的几何特征;由浅入深,在问题解决的过程中体会并深化转化与化归、函数与方程、数形结合等思想;过程的积累与方法的掌握关键在于反思和实践.所以,注重基础知识的积累,引导学生去体验并经历知识的发生与发展过程,积极总结反思形成能力是教学活动应该坚持并遵循的基本原则[1].

7.2 研究考题,创设探究性学习活动

学习的目的在于提升能力,结果将付诸于实际运用.引导学生学会是教学活动的基础,发展能力是阶段性教学目标,关键要引导学生学会主动学习.圆锥曲线中的一些定点定值问题是高考考查的重点,承载着试题的主要区分功能,解决这些问题往往需要具有较强的数学运算与数学建模能力,而这些能力的形成和发展离不开必要的探究性学习过程.探究性学习活动往往需要在有计划有组织的前提下开展,文章所呈现的试题研究过程就可以作为探究性学习活动组织学生学习.所以探究性学习课程的开发离不开研究试题,尤其是研究高考试题,在研究中体会命题者的思想,思考命题规律,寻找教学增长点.

7.3 注重过程性教学

过程性教学强调回归问题的本质,回归知识的发生与发展过程.问题解决过程中有意识的追问本质是什么,能不能进行特殊化或者一般化,能不能将结论进行迁移或者推广就显得很重要[2].在阶段性学习过程中,基于学生的元认知发展水平,由浅入深,实现知识与能力的层级递进式发展;在复习备考阶段,以点带面,尝试多角度探究同一个问题,甚至可以是一题一课或者一题多课,实现知识的横向迁移,引导学生构建知识体系,形成关键能力.遵循从特殊到一般、从具体到抽象、从简单到复杂的探究原则,厘清知识的发生与发展逻辑,体验知识的发生与发展过程,夯实过程,积累活动经验,将学习者的角色适当加入一点研究者的元素,在研究中学习,在学习中开展研究,进而实现素养的真正提升.