隐藏在平行线间的“拐点”问题

广东省深圳市光明区高级中学(518107) 林晓珊 刘 成

平行线是初中数学的几何初步,但其中的“拐点”问题让许多学生都不知所措.“拐点”问题经常需要作辅助线,这对于初步接触几何的学生来说,是一大难题的开始.因此本文首先将“拐点”问题的几种类型进行汇总,总结出常用的辅助线作法,在帮助学生提高对题目的理解与提高解题效率的同时,拓展学生的思维.

1 “拐点”的本质

“拐点”问题实质上是一个动点(即拐点)位于平行线的不同位置所产生的不同模型.

如图1,2,AB//CD,动点P在AB、CD任意之间,由此会产生如下模型.作者将这几种模型划分为两大类:

一类是动点P位于两条平行线之间(如图1,其中①为凸形图,②为凹形图);

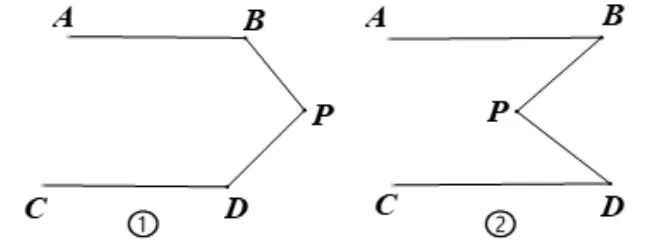
图1

一类是动点P位于两条平行线外部,称为外错型(如图2,其中①②P点位于平行线上方,③④P点位于平行线下方).

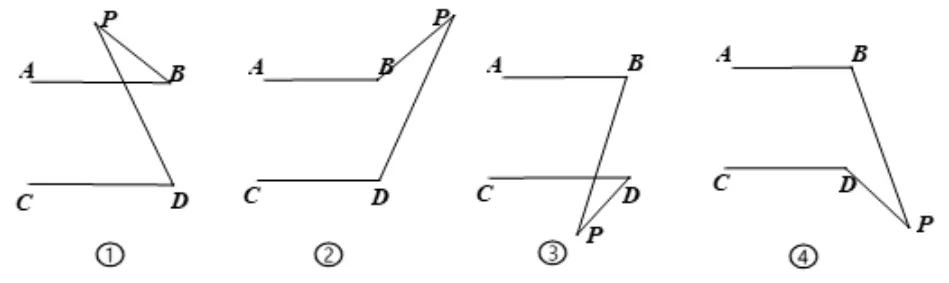
图2

2 “拐点”解法分类

2.1 凸形图

常用解法一:过点P(即拐点)作直线EP//AB(如图3).

常用解法二:连结BD(如图4).

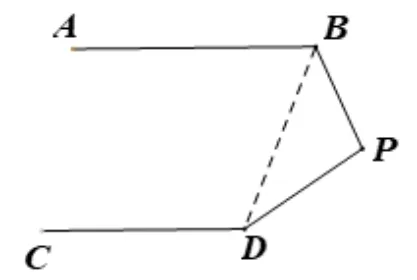
图4

小结论一:∠BPD+∠B+∠D=360°

证明一(如图3) :∵AB//CD,EP//AB,∴EP//CD,∴∠D+∠EPD= 180°,又∵EP//AB,∴∠B+∠EPB=180°,∴∠B+∠EPB+∠EPD+∠D=180°+180°=360°,即∠BPD+∠B+∠D=360°.

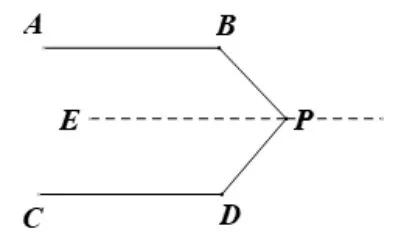
图3

证明二(如图4):∵ΔBDP是一个三角形∴∠BPD+∠PBD+ ∠BDP= 180°,又∵AB//CD,∴∠ABD+∠BDC=180°,∴∠ABP+∠CDP+∠BPD=360°.

2.2 凹形图

常用解法一:过点P(即拐点)作直线FP//AB(如图5).

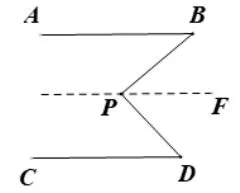
图5

常用解法二:连结BD(如图6).

图6

常用解法三:延长BP交CD于点G(如图7).

小结论二:∠B+∠D=∠BPD

证明一(如图5):利用两直线平行,内错角相等即可证明;

证明二(如图6) :∵AB//CD,∴∠ABD+ ∠BDC=180°,又∵∠1+∠BPD+∠2=180°,∴∠ABP+∠PDC=∠BPD.

证明三(如图7) :∵AB//CD,∴∠B= ∠1,又∵∠1 +∠D=∠BPD,∴∠B+∠D=∠BPD.

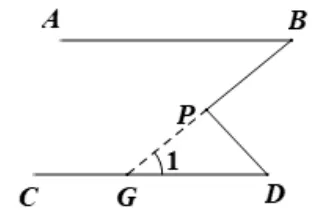
图7

2.3 外错型

如图2,外错型主要分为两大类:点P在平行线上方和下方,类型一致,因此本文只着重讲点P在上方,另外一种情况类似.但点P在平行线上方又分为图8,图9 两种情况.

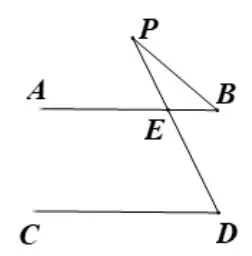
图8

常用解法一:不用作辅助线(如图8)

小结论三:∠D=∠P+∠B.

证明(如 图8) :∵AB//CD,∴∠D= ∠PEA,又∵∠PEA=∠P+∠B,∴∠D=∠P+∠B.

常用解法一:延长AB交PD于点E(如图9)

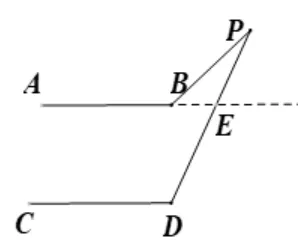
图9

常用解法二:延长PB交CD于点F(如图10)

图10

小结论四∠ABP=∠D+∠P.

证明一(如 图9) :∵AB//CD,∴∠D= ∠PEA,又∵∠ABP=∠PEA+∠P,∴∠ABP=∠D+∠P.

证明二(如图10):∵AB//CD,∴∠PBA= ∠PFC,又∵∠PFC=∠D+∠P,∴∠ABP=∠D+∠P.

2.4 复杂“拐点”问题

作者在上述文章中将“拐点”问题的基本模型与基本解决进行一定的梳理,但实际题目往往并不如此直白,需要进行变形转化方可求解.解决复杂拐点问题,关键要引导学生学会在实际问题中将模型寻找出来.具体方法可以概括为两步:

首先，找一组平行线.这是拐点类问题的基础,也是该模型的主要特征.

其次，寻找拐点.在平行的基础上找到与问题相关的拐点,从而运用模型知识解决问题.

作者对日常考查“拐点”的常见题型进行分类、梳理如下:

2.4.1 组合“拐点”

例1如图11,已知直线l1//l2,∠A=125°,∠B=105°,则∠1+∠2=____.

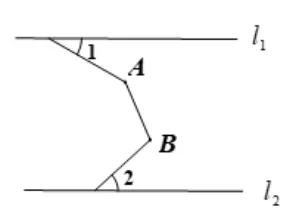
图11

分析:本题实质上是两个“凸形图”的融合,故从两个角度——作平行线、连结端点来考虑.

解法一(如图12) 过点A作直线l3//l1,过点B作直线l4//l1,由平行线的传递性可知,l1//l2//l3//l4,∴∠1 =∠3,∠2=∠4,由图可知∠A+∠B=∠3+∠5+∠6+∠4=230°,∴∠1 + ∠2 = ∠3 + ∠4 = 230° -180°= 50°,即∠1+∠2=50°.

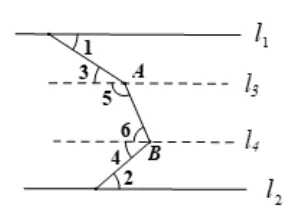
图12

解法二(如图13)连结CD,∵∠A+∠B=230°,又∵四边形内角和为360°,∴∠3+∠4=360°-(∠A+∠B)=130°,又∵l1//l2,∴∠1+∠2=180°-(∠3+∠4)=50°.

图13

点评:本题的关键在于要学会看清楚这是两个“凸形图”的融合,借用两次模型即可解决问题.

例2如图14,已知AB//CD,BF平分∠ABE,DF平分∠CDE,若∠BED=115°,则∠BFD的度数是____.

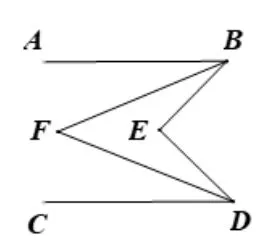
图14

总体分析:本题实质上是两个“凹形图”的组合体,将两个组合拆开,分别应用常用解法即可.

解(如图15) 将本图组合图形拆开,形成如图15(1) (2) 由于结论一可知:∠1 + ∠2 = ∠BED= 115°,∠BFD=∠3+∠4,又∵BF平分∠ABE,DF平分∠CDE,∴∠3+∠4=×115°=57.5°.

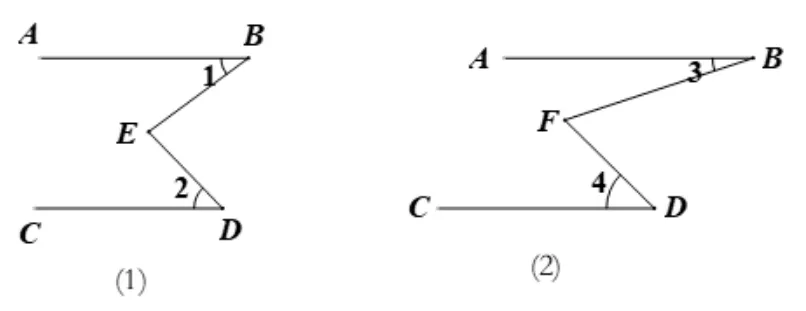
图15

另外解法:可以过点E,F作平行线,也可延长BE,BF,亦可连接BD,以上几种解法均不如直接运用结论快捷简便,故此处不展开分析.

点评:本题的关键在于能够将组合图形拆开,例1 与例2 的共同点在于均是两个“拐点”基本模型的重合,区别在于例1 是两个“凸形图”直接链接,例2 是两个“凹形图”互相嵌套,但只要能够从具体题目提炼出“模型”,问题自然会迎刃而解,因此,学生对于基本模型的掌握显得尤为重要.

例3如图16,一条公路修到湖边时,需拐弯绕湖而过,若第一次拐角∠A= 130°,第二次拐角∠B= 150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C=______.

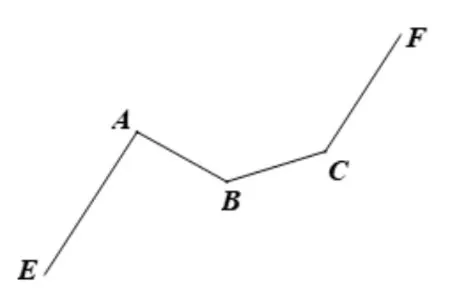
图16

总体分析:本题实质上AE,CF两个平行线之间存在B拐点问题,且不同于例1 和例2,本题是“凸形图”和“凹形图”的组合图.提炼模型时,我们可以将AE以及CF这一组平行线延长成直线,如图17,这样能使得该模型更加直观.

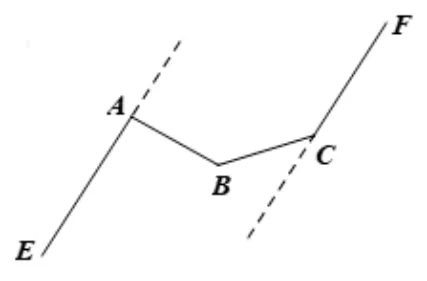
图17

解法一(如图18) 过点B作BG//CF,由题可知,AE//BG//CF,∴∠A= ∠ABG= 130°,∠GBC= 20°,∴∠C=180°-∠GBC=160°.

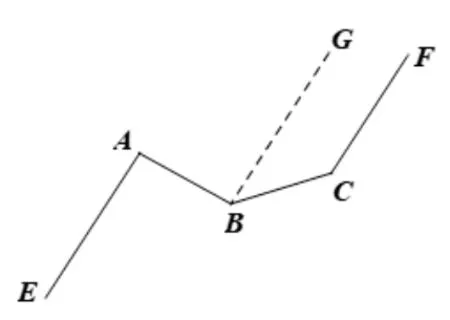
图18

解法二(如图19) 延长AB,FC交于点H,∴∠A=∠AHC= 130°,∠ABC= ∠AHC+ ∠BCF= 130°+∠BCF,∴∠C=180°-∠BCH=160°.

图19

2.4.2 三角板中的“拐点”

例4在综合与实践课上,老师请同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF= 60°)”为主题开展数学活动.如图20,小颖把三角尺的两个锐角顶点E,G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系.

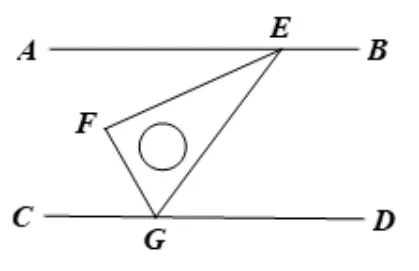
图20

本题实质上可以转变为如图21,即为“凸形图”,由结论一可知∠AEF+∠FGC= ∠EFG= 90°,证明方法可以参考结论一的三种证明方法,此处不再展开论证.

图21

例5小红把一副三角板摆成如图22 的样子,则∠AED=_____.

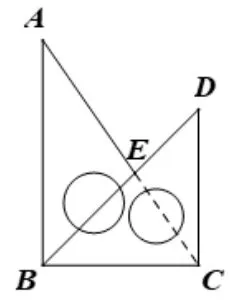
图22

本题实质上可以转变为如图23,即为“凸形图”,由结论一可知∠AED=∠A+∠D=75°,类似例4.

图23

例6如图24,∠D=∠B=90°,∠E=45°,∠A=30°,则∠AFD=____.

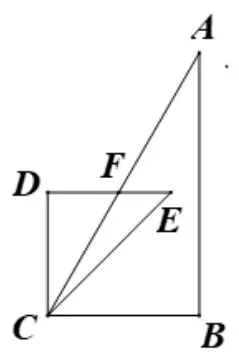
图24

本题实质上可以转变为如图25,即为“凸形图”,由结论一可知∠AFD=∠A+∠D=120°,类似例5.

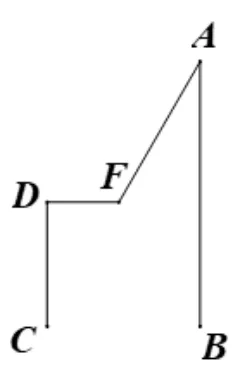
图25

点评:由例4,例5,例6 可以对比可知,部分三角板问题可以简化为“拐点”问题,将复杂问题简单化,可以更加快捷简便的算出.

3 教学建议

3.1 专题突破要先模型,后题型

“拐点”问题作为平行线中的专、难题,需要教师带领学生进行规范化学习,才能对该问题进行突破.

教师应首先借助几何画板,通过动点的形式展示出几种“拐点”的模型,让学生从整体的角度理解几个模型之间的区别与联系.

接着,教师再分门别类对几种类型进行专项讲解,帮助学生梳理形成关于“拐点”问题的基本模型与解法,形成体系.

最后进行分类题型的攻克,让学生逐渐适应、熟悉模型,学会在复杂问题中提炼、判断出模型,并解决问题.

3.2 模型掌握要先通法,后特法

由上述三种模型不难发现,三种模型最常用的解法均为过拐点作平行线,因而该作法为解决拐点问题的通法.但在一些问题中,延长与连结也可以使问题更简化.

因此在教学过程中,教师要引导学生首先掌握通用法,进而熟悉特殊方法.在解题过程中,以通法为主,特法为辅,才能让学生在千变万化的题海中游刃有余.同时,多种解决方法的渗透,也能够在一定程度上培养学生的发散思维.

3.3 攻克题型要先分类,后总结

从作者总结的题型来看,对于拐点问题的考查趋向于“组合拐点”或者套用实际问题的外壳,由此来“迷惑”学生.因此,让学生学会从复杂问题中提炼出模型显得尤为重要.

在实际的训练过程中,教师可以先将问题进行分类,通过同一种类型的问题让学生首先适应、掌握并学会运用模型,并开始培养学生提炼模型的能力.

接着引导学生对分类问题进行总结、回顾、训练,这样才能够逐步培养学生复杂问题简单化的能力,做到问题一击即破.