几个常见问题的“秒解”例析
2022-01-10广州中学510640陈汉桥
广州中学(510640) 陈汉桥
数学家波利亚曾说:“没有任何一道题目是可以解决得十全十美的,总剩下些工作要做,经过充分的探讨总结,总会有点滴的发现,总能改进这个解答;而且在任何情况下,我们总能提高对这个解答的理解水平[1].”多年的教研活动实践中,与老师们交流的常见观点之一,就是大学所学知识在中学教学中少有用得上的,果真其然吗,非也! 这些层面都要求老师们需要不断提高自己的教学水平,努力提高解题能力,而借助于“高观点”解题不失为一种救急的解决办法,本文拟从几个小问题出发,小议课堂教学中学生们提出的几道疑难题的“新”解法,与同仁分享.
问题1:运用中线或角平分线长公式解题
多年前,在奥校上课时,经常碰到学生问一些难题,而这些“难题”其实并不很难;说它不难,其实是在理解了较多奥数里出现的公式前提下,有的难题是可以实现“秒解”的,比如下例1:
例1如图,圆O的半径为3,点A,B都在圆O上,已知AB= 4,且C为AB延长线上一点,BC=4,点D为圆O上一点,求AD2+DC2的最大值.
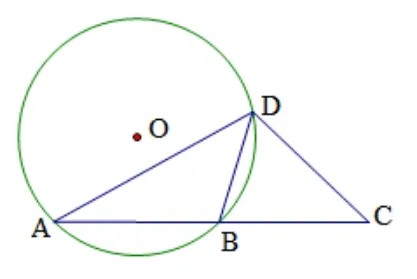
显然,若熟知中线长公式ta=即可推出DA2+DC2= 4DB2+AC2= 4DB2+64,∴当DB=6 时(DB为直径),AD2+DC2=最大.
练习:已知⊙O是ΔABC的内切圆,AB= 4,∠C=60°,试求⊙O的面积的最大值;
问题2:例2(英国1995)已知a、b、c为满足下列条件的实数,a <b <c,a+b+c= 6 且ab+bc+ac= 9,证明:0<a <1<b <3<c <4[2].
解法分析一:只证明0<a <1,显然a <2,c >3;当a=0 时,b=c=3 矛盾;由
知道b、c是方程x2-(6-a)x+9-6a+a2=0 的两个不等实数根,于是Δ = (6-a)2-4(9-6a+a2)>0,解得,0<a <4,即0<a <2,由b >a,>3a-6,3a-6<0,解得a <1,其余略;

解法分析二:根据多项式零点和系数的关系,可设首一多项式:P(x) =x3-6x2+9x - k,其中,k=abc,下面只需要找出多项式P(x)的零点,因a、b、c的符号没有确定,从而多项式的系数的符号也没有确定,故没能画出y轴,但是能确定:当x足够大时,函数值将是正的,当x足够小时,函数值将是负的,由于三个零点之间满足关系a <b <c,所以,P(x)在a、b之间应该取正值,而在b、c之间应该取负值,同时,存在u ∈(a,b),f(u)取极大值;存在v ∈(b,c),f(v)取极小值;
通过对P(x) 求一阶导数,P′(x) = 3x2-12x+9 =3(x-1)(x-3),所以,u= 1,v= 3.同时,有f(1)>0,f(3)<0,所以,a <1<b <3<c,
下面再证明另外两个不等式a >0 和c <4,为此,只需要证明P(0)<0,P(4)>0,这个是很容易的,由P(1) = 4-k >0,P(3) =-k <0,0<k <4,因此,得到P(0)=-k <0,P(4)=4-k >0,证毕.
问题3,如何求S1=1+2+3+···+n?
例3S2=12+22+33+···+n2,S3=13+23+33+···+n3,···,求这些数列的通项公式.
显然利用(n+1)2-n2=2n+1,可以求S1,其余依此类推,这种方法基础简单,学生容易接受,但是,对于求例4S4=1×2+2×3+3×4+···+n(n+1),可能就有难度;而且所求表达式还可以升级难度;这里就要利用拉格朗日插值定理来解决,基本就是秒杀的.具体如下:
记f(n) =S2,由f(1) = 1,f(2) = 5,f(3) = 14,f(4)=30,于是,得到:
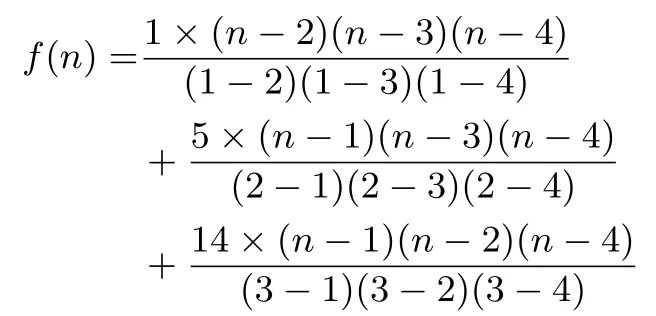

问题4:例5已知(a+c)(a+d)=(b+c)(b+d)=1,且a/=b,求证:(d+a)(d+b)=-1,(c+a)(c+b)=-1.
解法分析:本题可由初等变形方法直接推得,显然,下面的方法来得更简单快捷,a和b可以看做一元二次方程(x+c)(x+d)=1 的两个实数根,即有,(x+c)(x+d)-1=0,且有(x+c)(x+d)-1=(x-a)(x-b)再分别令x=-c,x=-d,即可得证.
问题5:例6绝对值不超过100 的全体有理数之和是多少?
这题来自北京海淀区出的教学资料.原题是:绝对值不超过100 的全体整数之和是多少? 答案是0,第二年该书再版时,原作者把这道题目改成上面的例6,答案仍然是0! 殊不知,这一改就成了一道错题了! 文[3]中,有详细分析讲解,这里只抽出介绍点滴条理,具体如下:
由S=1++…,知道无穷数列S收敛到2,而T=1++…发散到∞,再看

可知0<L <1,数列收敛L=ln 2.
如果运用加法交换律,经过变形,可以得到:
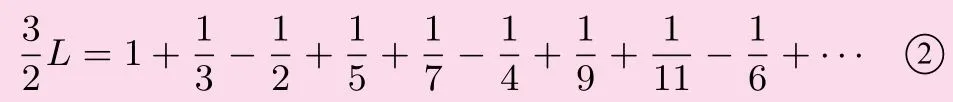
于是比较①②,立即可以发现,右边相等,但是左边不同,这是什么原因呢?
数学上有一个“黎曼定理”,这个定理意思是讲绝对值收敛的无穷和,无论按怎样的顺序做加法,其和不变,而条件收敛的无穷和,可以通过交换它的项,让它收敛到任一指定的数,也可以让它发散到+∞或-∞.
以上仅仅从几例的解答分析中,感受利用牵涉到了的高等数学知识或超纲的理论公式,来解题的便利、快捷和高效;事实上,不论小学或中学的奥数问题中,有许多这样的案例,只要略加思考,提出变式,比如加元、改变维数、数形互换,等等,题目的难度就立即提升很多,甚至可达到运用对应所学知识都解答不了的地步,如例,试写出数列-1,-2,-3,4,-5,-6,-7,8,…(三负一正)的通项公式,答案竟然是作为一名普通的数学老师,还是应该不忘初心,牢记教育责任,坚持教学研究,去努力提高对新的解答的理解水平.
