具有恐惧效应和阶段结构的时滞捕食者-食饵模型
2022-01-10刘白茹刘俊利
刘白茹,刘俊利,吕 潘
(西安工程大学 理学院, 陕西 西安 710048)
0 引 言
在自然界中,捕食现象是最为普遍的一种,也是当前研究的热点问题。随着捕食者-食饵模型研究的深入,不同类型的捕食者-食饵模型被提出[1-4]。在研究捕食者-食饵模型时,考虑物种的阶段结构十分必要[5-7]。种群在不同的阶段会表现出不同的生理特征。一般来说,研究者们会将食饵或捕食者分成幼年和成年2个阶段进行考虑。种群从幼年到成年的过程,会经历一段时间间隔,称之为种群从幼年到成年存在成熟时滞。2016年,宋燕等研究了一类具有阶段结构及B-D功能反应的捕食者-食饵模型,讨论了在一定条件下,当τ通过临界值τ0时,正平衡点将改变其稳定性,产生Hopf分支[8]。
除了种群的阶段结构和时滞对模型的影响,当捕食者出现在食饵面前时,食饵会对捕食者产生恐惧,食饵的出生率会受到影响,从而影响食饵种群规模的大小。此时,捕食者对食饵的影响程度甚至超过直接捕杀的效果[9-11]。2011年,ZANETTE等通过歌雀实验,证明了仅仅由于对捕食者产生的恐惧,导致成年歌雀的繁殖数量减少了40%[12];2016年,WANG等首次提出了具有恐惧效应的捕食者-食饵模型,理论分析及数值模拟结果表明,恐惧效应会使系统更加稳定[13]。2017年,WANG等还提出了一个具有恐惧代价和适应躲避捕食者代价的捕食模型[14]。数学分析表明,恐惧效应与时滞的相互作用,共同决定了种群的长期动力学行为:当时滞处于中间值时,正平衡态可能失去稳定性;而当时滞较大时,正平衡可能恢复其稳定性。2018年,王蓉等考虑了一类带有恐惧效应的捕食者-食饵模型的共存态问题[15]。利用谱分析和分支理论的方法,以捕食者的死亡率m为分支参数,讨论了系统在半平凡解附近出现分支现象。
在上述文献的基础上,本文考虑食饵具有阶段结构,将食饵从幼年到成年的成熟时滞与恐惧效应相结合,并考虑捕食者对食饵的功能反应,以幼年食饵的出生率r和恐惧因子k作为分支参数,研究一类时滞微分方程模型。
1 模型的建立
(1)
式中:x1(t)、x2(t)、y(t)分别表示幼年食饵、成年食饵和捕食者在t时刻的密度;r为幼年食饵的出生率;τ为幼年食饵成长为成年食饵的成长期;d1、d2、d3分别为幼年食饵、成年食饵和捕食者的死亡率;a为成年食饵内部竞争导致的死亡率;n为捕食者捕食食饵后转化为自身生物量的转化率。r、d1、d2、d3、a、m、n、b为正常数,k、τ为非负常数。
一般来说,成年食饵会将幼年食饵保护起来并喂养它们,因此幼年食饵受到捕食者的攻击可以忽略不计,故在模型(1)中假设捕食者种群仅以成年食饵为食。模型(1)的初始条件为:
x1(θ)=φ1(θ)≥0,x2(θ)=φ2(θ)≥0,
y(θ)=φ3(θ)≥0,θ∈[-τ,0]
(2)
设φ=(φ1(θ),φ2(θ),φ3(θ))∈C+=C([-τ,0];R3,R=[0,+∞)),C+表示从[-τ,0]到R3,R=[0,+∞)的连续函数所组成的Banach空间。对于连续函数u:[-τ:σφ)→R3,σφ>0,当t≥0时,定义
ut(θ)=u(t+θ),∀θ∈[-τ,0]
定义集合
下面给出模型解的存在性、非负性和有界性。
引理1[16]考虑时滞微分方程
I′(t)=cI(t-τ)-dI(t)-hI2(t)
其中c,d,h,τ>0,当t∈[-τ,0]时,有I(t)>0,则有:
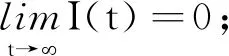
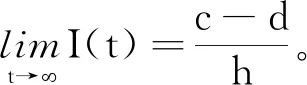
定理1∀φ∈X,模型(1)有唯一的非负解u(t,φ),u0=φ,t∈[0,+∞)。
证明给定φ∈X,定义G(φ):=(G1(φ),G2(φ),G3(φ)),其中
d1φ1(0)
∀φ∈X,G(φ)在R×X中每个紧集上都是连续的,关于φ是李普希兹连续的。由文献[17]中定理2.3可知,∀φ∈X,模型(1)通过点(0,φ)的解在其最大存在区间[0,σφ)是唯一的。
对模型(1)中第1个式子求解得到
当φ∈X,φi(0)=0时,有Gi(φ)≥0,i=2,3;根据文献[18]中定理5.2.1可知,∀t∈[0,σφ),ui(t,φ)≥0,i=2,3。因此,∀t∈[0,σφ),x1(t)≥0,则模型(1)的解是非负的。
下面证明模型(1)满足初始条件(2)的正解是最终有界的。
由模型(1)第2个方程可知

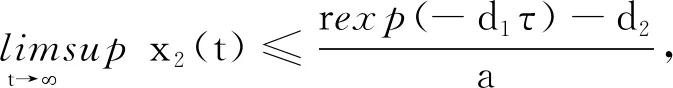
令
L(t)=nx1(t)+nx2(t)+y(t)
当t>T1时,得
其中u*=min{d1,d2,d3},则当t>T2时,由比较定理知
因此x1(t)、x2(t)、y(t)有界 ,则σφ=∞。
2 平衡点的存在性和稳定性
令模型(1)右边的表达式等于零,计算得:
1) 模型(1)总存在灭绝平衡点E0(0,0,0)。
2) 当rexp(-d1τ)-d2>0时,模型(1)存在边界平衡点E1(x11,x21,0),其中:
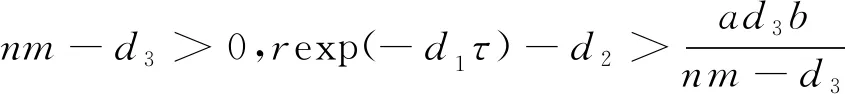
令E(x1,x2,y)是模型(1)任意一平衡点,则点E对应的特征方程为
(3)
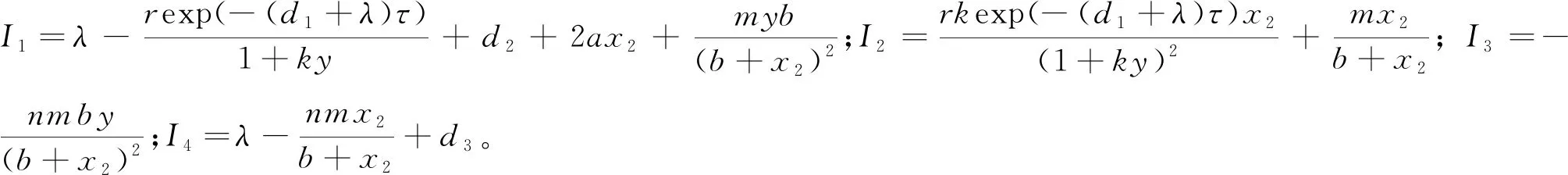
定理2当rexp(-d1τ)

(λ+d1)(λ-rexp(-(d1+λ)τ)+
d2)(λ+d3)=0
(4)
方程(4)有2个特征值λ1=-d1,λ2=-d3,其他特征根满足方程
λ-rexp(-(d1+λ)τ)+d2=0
(5)
当τ=0时,式(5)式变为λ-r+d2=0,λ3=r-d2。当r
当τ>0时,令λ=iω,ω∈R,代入式(5)中得到
iω-rexp(-(d1+iω)τ)+d2=0
分离实部与虚部得到
将此式分别平方后相加,得
ω2=(rexp(-d1τ)-d2)(rexp(-d1τ)+d2)
(6)
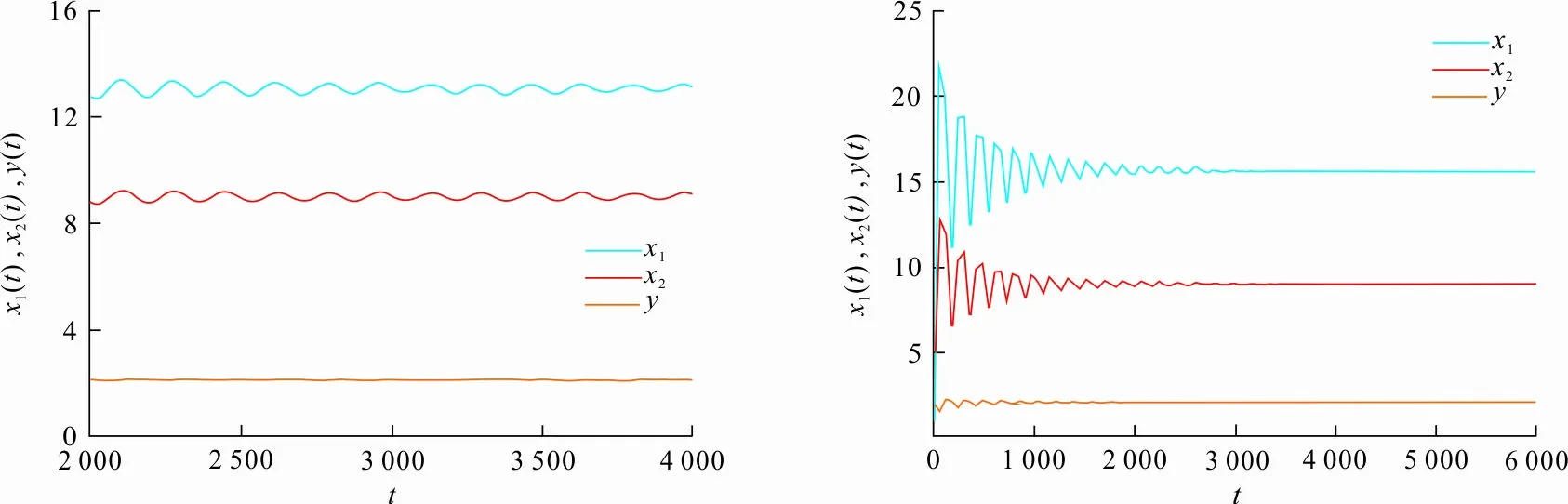
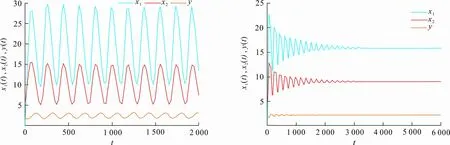
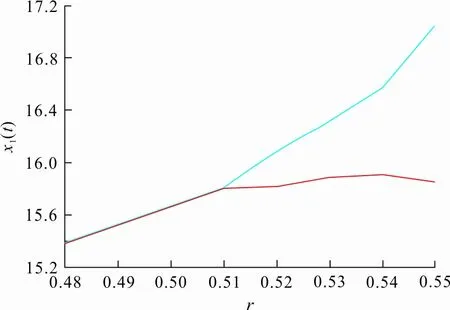
当rexp(-d1τ) 定理3当rexp(-d1τ)>d2时,边界平衡点E1存在。 ⅰ) 当nm-d3≤0时,平衡点E1是局部渐近稳定的; 证明将RE1代入式(3)中,得到边界平衡点E1所对应的特征方程 (λ+d1)(λ-rexp(-(d1+λ)τ)+d2+2ax21)· (7) 1) 若nm-d3≤0,此时显然λ2<0。 2) 若nm-d3>0,则当 时,λ2<0; 当 时,λ2>0。 特征方程(7)的其他根满足方程 λ-rexp(-(d1+λ)τ)-d2+ 2rexp(-d1τ)=0 (8) 当τ=0,式(8)变为λ+r-d2=0,则λ3=d2-r<0,特征方程(7)的所有根均为负数。当τ>0时,令λ=iω,ω∈R,代入式(8)中得到 iω-rexp(-(d1+iω)τ)- d2+2rexp(-d1τ)=0 (9) 将式(9)实部与虚部分离并整理得到 ω2=(-rexp(-d1τ)+d2)· (3rexp(-d1τ)-d2)<0 故方程(9)无实数解,即方程(8)的根均具有负实部。 综上所述,在定理3的ⅰ)、ⅱ)条件下,∀τ≥0,点E1所对应的特征方程(7)只有负实部的根;在定理3的ⅲ)条件下,因为λ2>0,平衡点E1不稳定,因此定理3成立。 则当k4-k3>0时,正平衡点E*是局部渐近稳定的;当k4-k3<0时,当τ从0增加时,E*可能失去稳定性。 证明将RE*代入式(3),得到正平衡点E*所对应的特征方程 (10) 方程(10)有一个特征值λ1=-d1<0,其余特征值满足方程: λ2+k1λ+k2exp(-λτ)λ+ k3exp(-λτ)+k4=0 (11) 式中: 当τ=0时,式(11)变为 λ2+(k1+k2)λ+k3+k4=0 (12) 当τ>0时,令λ=iω,ω∈R,代入式(11)并分离实部与虚部,得到 (13) 整理得 (14) 式中: z=ω2 则 1) 当k4-k3>0时,方程(11)没有纯虚根,∀τ>0,正平衡点E*局部渐近稳定。 2) 当k4-k3<0时,方程(11)有一组纯虚根±iω0,当τ从0增加时,E*可能失去稳定性。其中 是方程(14)唯一的正根。因此定理4成立。 定理5当rexp(-d1τ) 证明设(x1(t),x2(t),y(t))是模型(1)满足初始条件式(2)的正解。由模型(1)第2个方程得 综上所述,E0是全局吸引的,结合E0局部渐近稳定性,得平衡点E0是全局渐近稳定的。 定理6当rexp(-d1τ)>d2且定理3中条件ⅰ)或条件ⅱ)成立时,平衡点E1是全局渐近稳定的。 证明由模型(1)第2个方程得 2) 当条件ⅱ)成立时,有nm-d3>0, 当t>t3+τ时,由模型(1)中第2个方程可知 由引理1和比较定理知 由ε1的任意性可知 于是对于上述ε1>0,∃t4>t3+τ,当t>t4时,x2(t)>x21+ε1。因此 由模型(1)中第1个方程,当t>t4+τ时,有 rexp(-d1τ)(x21+ε1)-d1x1(t) 由比较定理和ε1的任意性可知 因此 综上所述,E1是全局吸引的,结合E1的局部渐近稳定性知,边界平衡点E1是全局渐近稳定的。 定义: X0={φ=(φ1,φ2,φ3)∈X|φ3(0)>0且∃θ0∈[-τ,0],使得φ2(θ0)>0} X1={φ∈X|φ3(0)=0} X2={φ∈X|φ3(0)>0,φ2(θ)≡0,∀θ∈[-τ,0]} 则X=X0∪X1∪X2。 定理7假设nm-d3>0, (nm-d3)(rexp(-d1τ)-d2)>ad3b 证明首先证明X0,X1,X2关于系统(1)是正不变的。因为 因此,若y(0)=φ3(0)>0,则y(t)>0,∀t≥0;若y(0)=φ3(0)=0,则y(t)≡0,∀t≥0。所以X1是正不变的。 由模型(1)第2个式子得 (15) y(t)有界,因此若x2(t)是持久的,则x1(t)也是持久的。 令∂X0=X1∪X2,模型(1)中具有初值(φ1,φ2,φ3)的解的ω极限集为ω(φ1,φ2,φ3)。记Ω=∪{ω(φ1,φ2,φ3)|(φ1,φ2,φ3)∈∂X0},则在∂X0上: 1a) 若rexp(-d1τ) 2) 若φ∈X2,则x2(t)≡0,∀t≥0。因此当t→+∞时,有x1(t)→0,y(t)→0,即 (x1(t),x2(t),y(t))→RE0=(0,0,0) 因此Ω={RE0,RE1},若RE0、RE1是孤立的,则Ω也是一个孤立的非循环覆盖。RE0与RE1的孤立不变性可以从式(16)的证明中得到,即 Ws(RE0)∩X0=∅,Ws(RE1)∩X0=∅ (16) (17) 因为rexp(-d1τ)>d2,因此∃ε>0,使得 (18) 由引理1、比较定理和式(18)得 这与式(17)矛盾,所以Ws(RE0)∩X0=∅。 (19) 因为(nm-d3)(rexp(-d1τ)-d2)>ad3b,该不等式等价于(nm-d3)x21>d3b,则存在充分小的η>0 (η (20) 由方程组(1)中第3式得 为了了解不同的参数对系统动力学的影响,利用Matlab软件进行数值模拟,验证理论结果的正确性。选取一组参数值(Ⅰ): r=0.2,d1=0.02,d2=0.1,d3=0.21,m=0.3, n=0.8,a=0.01,k=0.1,b=1,τ=0.1 图1(a)、(b)、(c)分别表示系统(1)在灭绝平衡点E0(0,0,0)、边界平衡点E1(0.199 0,9.960 0,0)以及在正平衡点E*(0.001 8,5,0.722 9)处的稳定性。 (a) d2=0.2,其余参数值同(Ⅰ) 图1(a)选取d2=0.2,其余参数值同(Ⅰ),此时rexp(-d1τ)-d2=-0.000 399 6<0,满足定理5中条件,系统在点E0处是全局渐近稳定的;图1(b)选取d3=0.24,其余参数值同(Ⅰ),此时 rexp(-d1τ)-d2=0.099 6>0 nm-d3=0,满足定理6中的条件,系统在点E1处全局渐近稳定;图1(c)选取参数值(Ⅰ),此时 nm-d3=0.04>0 k4-k3=0.001 2 满足定理4中局部稳定性条件,即系统在点E*处是局部渐近稳定的。 选取另一组参数值(Ⅱ): r=0.5,d1=0.02,d2=0.1,d3=0.18,m=0.4, n=0.5,a=0.01,k=0.3,b=1,τ=6 通过数值模拟得到不同的图像, 如图2、3所示。 图2、3分别表示了系统(1)在时滞τ及恐惧因子k变化时, 对食饵种群和捕食者种群数量的影响。 (a) τ=5,其余参数同(Ⅱ) (b) 参数值(Ⅱ) (a) k=0.2,其余参数同(Ⅱ) (b) k=0.28,其余参数同(Ⅱ) 当系统(1)中幼年食饵到成年食饵的成熟时滞τ发生改变时,系统的稳定性也会随之发生改变,如图2(a)、(b)所示。当τ=5时,系统(1)在正平衡点周围出现周期性震荡,存在周期解,系统不稳定;当τ=6时,随着τ的增加,系统(1)逐渐趋于稳定。 随着成年食饵对于捕食者的恐惧程度k的变化,系统(1)的动力学行为也随之改变,如图3(a)、(b)所示。当k=0.2时,系统(1)在正平衡点处出现周期性震荡,存在周期解;而当k=0.28时,系统(1)逐渐趋于稳定。 为了研究当系统(1)在正平衡点附近出生率r及恐惧因素k的影响,将出生率r和恐惧因子k分别作为分岔参数,得出关于r和k的分岔图,如图4、5所示。 图4中取初始值为(1,5,2),除变量r外,其他参数与参数组(Ⅱ)相同。从图4可以看出:对于幼年食饵出生率r,当r>0.51时,随着幼年食饵出生率的增加,系统原本的稳定性被破坏,食饵和捕食者的数量呈周期变化;当r∈(0.48,0.51]时,幼年食饵和捕食者的数量随着幼年食饵出生率r的增长而增加,而成年食饵种群趋于稳定状态。 (a) x1(t) 图5中取初始值为(1,5,2),除变量k外,其他参数同参数组(Ⅱ)。 (a) x1(t) 从图5可知:对于恐惧因子k,当k∈(0,0.28]时,系统(1)中幼年食饵、成年食饵和捕食者的数量呈周期变化,系统不稳定;当k>0.28时,随着恐惧程度的增加,食饵种群趋于稳定状态,恐惧效应不再对其产生影响。从生物学角度上,食饵对捕食者产生一定程度的恐惧后,由于习惯,恐惧效应在长期内不再会影响食饵种群,且捕食者种群随着k的增加而减少。 时,模型存在唯一的正平衡点E*。当定理4中的条件ⅰ)成立时,E*是局部渐近稳定的;当正平衡点E*存在且初值满足一定条件时,模型是一致持久的。最后,通过数值模拟验证了理论结果的正确性及时滞、出生率或恐惧因子改变时对系统动力学行为的影响。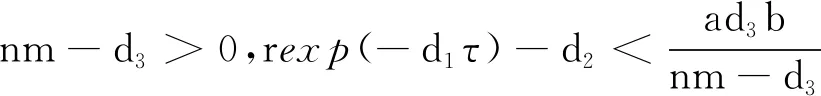
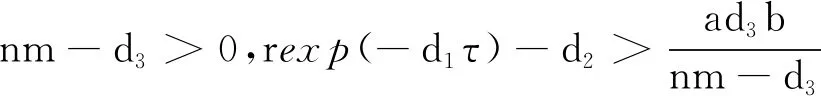
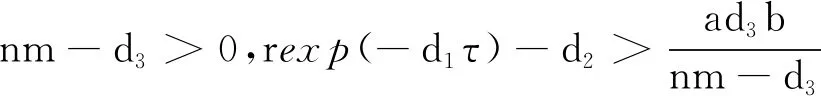
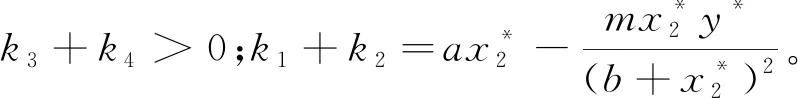
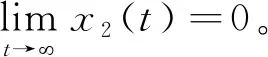

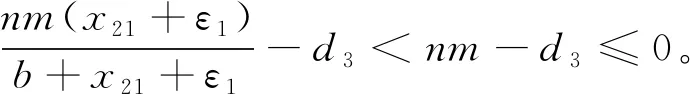
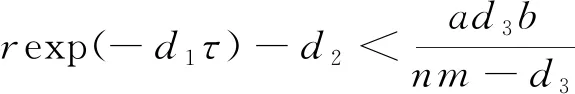
3 系统(1)的持久性
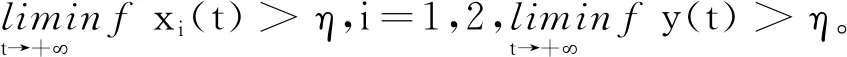

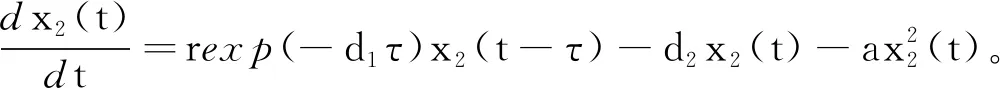

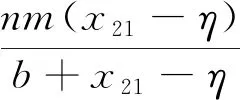
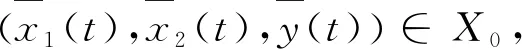
4 数值模拟


5 结 语

