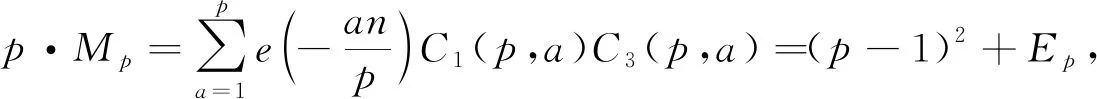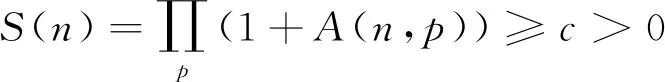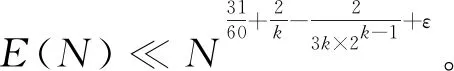一类不等幂次的Waring-Goldbach问题的例外集
2022-01-10朱豆豆
朱豆豆
(华北水利水电大学 数学与统计学院, 河南 郑州 450046)
1 引言与主要结果
混合幂Waring-Goldbach问题主要研究将正整数n表示为

式中:
2018年,文献[3]等将结果改进为
此外,文献[6-11]在这类问题的研究中取得了重要结果。同时,一些新的方法也发展起来,为此类问题的研究提供了更为有效的途径。本文主要应用圆法并结合文献[12]的思想,得到如下结果:
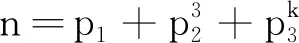
2 预备知识
为了清晰地说明定理1的证明思路,下面给出一些必要定义:
对于i=1,3,k,定义
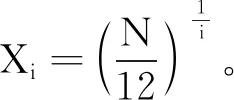
则∀Q>0,有
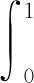
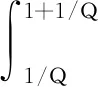
取
(1)
根据Dirichlet有理逼近定理,
有整数a,q满足1≤a≤q≤Q和(a,q)=1,有
定义主区间M和余区间m如下:
(2)
其中
则
则有:
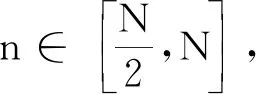
式中:S(n)是由式(6)定义的奇异级数,该奇异级数绝对收敛,且对于任意的奇数n和固定常数c*,有
0 (3) I(n)定义为 并且满足N1/3+1/k≪I(n)≪N1/3+1/k。 命题1的证明将在第4节给出,对奇异级数性质的讨论将在第5节给出。为了得到定理1,还需要以下引理: 引理1若P,Q满足式(1),余区间m如式(2)定义,则对k≥4,有 (4) 这里α满足条件 因为对于Q*的选取满足Q* 这2种情况均有q(1+N|λ|)≫P,所以式(4)可以化简为 最后的≪只依赖于式(1)中的P的选取。 定义可乘函数ωi(q)如下: 对于整数i≥3和集合A⊆(U,2U]∩N,定义 (5) 引理2[12]对于γ∈R以及X≤U,定义 则L(γ)≪X2U-i(logU)Ai,其中ci和Ai是依赖于i∈N的常数。 引理3[12]对于1≤a≤q≤Ui·21-i以及(a,q)=1,定义 M(q,a)={α:|qα-a|≤Ui(21-i-1)} 设M是区间M(q,a)的并,取 若G(α)和h(α)是周期为1的可积函数,g(α)=gA(α)如式(5)定义,m⊆[0,1)是一个可测集,则 由命题1, 记 应用引理1可得 其中M如引理3中定义。应用引理2可得 J0≪Lc 又因为 则 在证明命题1之前,首先引入一些符号。当i=1,3,k时,对于Dirichlet特征χmodq,定义 其中δχ=1或者0取决于Dirichlet特征χ是否为主特征。进一步,设 Ci(q,a)=Ci(χ0,a) C1(χ1,a)C3(χ3,a)Ck(χk,a) 记 (6) 定义集合Lj(j=1,2,…,8)如下: 则 I1+I2+I3+I4+I5+I6+I7+I8 (7) 其中 这里I1可以用常规方法估计,需用到如下引理: 引理4[14]当(a,q)=1时,对于Dirichlet特征χmodq,有 引理5对于i=1,3,k,设χimodri是原特征,χ0modq是主特征,r0=[r1,r3,rk],则 (8) 证明类似于文献[15]引理6.7的证明,式(8)左侧远小于 这里χ0modur0是主特征,并且 通过引理4,可得 因为 则 接下来估计I1。对于i=1,3,k,根据文献[16]引理4.8, (9) 将式(9)代入I1得 (10) 由估计 (11) 并且令r0=1,由引理5,式(10)中的余项远小于 其中ϖ>0。因此,式(10)可表示为 (12) 则接下来只需证明对于j=2,3,…,8, 用文献[17]中的迭代方法估计I2,I3,…,I8的贡献。为此,对于i=1,3,k,设 关于Ji(g)和Ki(g)的估计,有如下结论: 引理6当P、Q满足式(1)时,有 引理7当P、Q满足式(1)时,有 引理8当P、Q满足式(1)时,有 J1(1)≪NL-A 引理6~8的证明与文献[18]引理 2.2~2.4的证明类似,在此略去。 首先从I8开始估计,这是最复杂的一项。 其中χ0modq是主特征,r0=[r1,r3,rk]。对于i=1,3,k,当q≤P,Xi |W3(χ3,λ)|·|Wk(χk,λ)|dλ 在最后一个积分中运用柯西不等式,则 因为r0=[r1,r3,rk]=[[r1,r3],rk],应用引理6及引理8可得 (13) 在对I2,I3,…,I7估计时,需结合由式(9)、(11)得出的以下估计: 利用处理I8类似的方法,可得 (14) 结合式(7)、(12)、(13)、(14),命题1得证。 首先给出本节所需引理。对于i≥1,定义 引理9[19]若(p,a)=1,则 引理10对于(p,n)=1,有 (15) 证明记式(15)左侧为S,通过引理9,有 若i∈{3,k}时,有|Ai|=0,则S=0;否则, 由引理9知,二重的外部和不超过 ((3,p-1)-1)((k,p-1)-1)≤2(k-1) 因为对于主特征χ0modp,t(χ0)=-1,所以 综上, 引理11设同余方程 解的个数为Mp,则对于p≥11及任意的正偶数u,有Mp>0。 由引理9, 所以当p≥11时,|Ep|<(p-1)2,故Mp>0。 引理12设同余方程 (x1x2x3,p)=1 解的个数为L(p,n),则对于任意的正奇数n,有L(p,n)>0。 证明由引理11,当p≥11时,对于任意的正奇数n,同余方程 至少有一个解,故得L(p,n)>0;当p<11时,可以直接逐一验证知L(p,n)>0。 引理13A(n,q)是关于q的可乘函数。 证明由式(6)知只需证明B(n,q)是关于q的可乘函数。设q=q1q2,(q1,q2)=1,则 B(n,q1q2)= (16) 因为(q1,q2)=1,则 Ci(q1q2,a1q2+a2q1)= Ci(q1,a1)Ci(q2,a2) (17) 把式(17)代入式(16),得 引理14设A(n,q)如式(6)所示,则 2) 存在绝对正常数c*>0,对于任意的正奇数n,有 S(n)≥c*>0 证明由引理12,B(n,q)是关于q的可乘函数。则 (18) (19) 式中: 记R(p,a):=C3(p,a)Ck(p,a)-S3(p,a)Sk(p,a),则 (20) (21) 另外,若直接运用引理4,则 因此, (22) 令c3=max(c2,48k),则对于无平方因子的q, (23) 因此,由式(19)可得 则引理14中1)成立。并且由式(23)可得 (24)
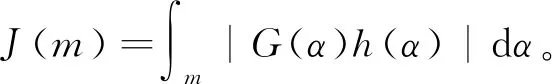
3 定理1的证明
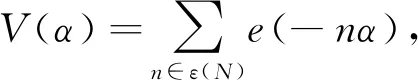
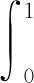
4 命题1的证明
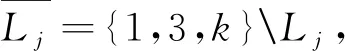

5 奇异级数