考虑预测误差的风电有功功率控制策略

张 义，彭佩佩，唐冰婕，陈 宁,王湘艳,韩楚晨

(1.国家电网有限公司，北京 100031；2.中国电力科学研究院有限公司，江苏 南京 210003;3.国网陕西省电力公司营销服务中心(计量中心)，陕西 西安 710199)

0 引 言

风力发电在我国经过连续多年的高速发展，目前已进入平台期，风电在电网适应性上的问题逐渐凸显。大规模的风电并网加重了电力系统安全稳定运行的压力，所以提升风力发电对电网的主动支撑性能，减轻其预测偏差对有功功率平衡控制的影响，已成为风力发电系统的核心问题[1]。

要实现风力发电系统对电网的主动支撑，需要风力发电站能够像传统电源一样具备良好的测量精度、控制性能和调节能力。首先，需极大地提升风力发电站功率预测水平，满足电网调度运行的精度要求；其次，需能够在满足电网稳定运行支撑的前提下，以新能源发电设备控制性能为约束，自动响应电网调节需求对风力发电站输出功率进行调整；最后，需及时响应电力系统运行状态的变化做出快速调节[2-3]。

目前，在风力发电站功率控制方面已有较多研究成果，大致可分为比例分配法和优化分配法2类[4-5]。双馈风电场具有频偏特性[6]，文献[7]以双馈风电机组运行特性为基础，提出了根据发电单元最大可用功率的风电场功率分配方法。文献[8-9]采用优化分配方法，设定不同的优化目标构建目标函数实现功率控制目标的分解。文献[10]提出了一种以风电场为对象的机组组合优化模型；文献[11]提出了风电场内风电机组的功率分配优化模型；文献[12]在文献[11]基础上引入模型预测控制和频率约束对优化模型进行完善。文献[13]重点考虑了调峰约束对优化模型的影响；文献[14]基于相邻调控周期风电机组运行状态的变化情况提出基于风电机组的状态分类模型，实现风电场功率的平滑输出。文献[15-16]介绍了风力发电功率控制系统的研发及其在实际工程中的应用。文献[17-18]设计了适应大型风力发电基地的功率控制体系，文献[19]开发了适应大型风力发电基地的新能源功率控制系统，根据风功率预测和电网下发的发电指令，以断面及线路稳定约束来对基地内的风电场发电功率进行分解。

以上的研究将风电预测功率认为是相对确定的。然而，风力资源自身具有随机波动性，预测功率也存在固有的误差，对风力发电站有功功率的准确控制提出了挑战。因此，在制定风力发电功率优化控制时需要合理的考虑预测误差[20-23]。实际运行过程中，由于空间相对分散及技术差异不同的风力发电站运行特性差异显著，误差分布特性不同[24-25]，准确掌握新能源的运行特性和功率预测误差分布特性对于提高新能源功率控制水平有重要意义。

据此，本文考虑不同新能源电站功率预测误差的差异，对风电有功功率控制进行优化。首先采集风电功率预测数据和实际运行数据，在此基础上对不同位置的风电场功率预测误差分布特性及其对有功功率控制的影响进行分析，基于不同误差分布特性对风电场有功功率控制进行整合优化。同时结合实际场景设计用于方法验证的案例，证明了方法的有效性。

1 风电功率预测误差分析

1.1 功率预测误差分布

根据风力发电站的预测功率Pf与实际功率Pa，可以计算得到预测功率的绝对误差。考虑到风电场出力较小时，较小的绝对误差可能造成较大的相对误差，不便进行统计分析，故取风电场额定功率Pwf为基准值来计算风电场的相对误差e，即

(1)

通过数理统计中的假设检验方法和χ2检验法验证后发现统计量测试值落在接受域中，故风电场预测功率误差服从正态分布。

1.2 功率预测误差置信评估模型

近年，越来越多的学者专家将分位数回归法和风险评估相结合应用于风力发电预测领域[26-27]。

分布函数F(y)=P(Y≤y)可以用于描述随机变量Y的性质，F(y)的τ分位数函数定义为

Q(τ)=inf{y:F(y)≥τ},0<τ<1

(2)

由式(2)可知，小于分位数函数Q(τ)的变量比例为τ，大于分位数函数Q(τ)的变量比例为(1-τ)。定义检验函数为

ρ(u)=τuf(u)+(τ-1)uf(u)

(3)

式中：当u≥0时，f(u)=0；当u<0时，f(u)=1。

设u=y-δ，对上式的左右两边取期望后再对δ求导：

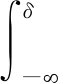
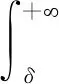
(4)

1.3 功率预测置信评估

给定分位数(τ1,τ2,…,τn)建立风电预测功率的分位回归模型，再结合风电功率误差的概率分布和置信水平即可得到风电功率预测误差的置信区间，进而得到风电预测功率的置信区间。由于功率预测模型及相关影响因素的不同，一段时间内不同风电场的预测误差分布呈现明显的不对称性。其中，部分风电场的预测功率与置信区间下边界十分接近，表明该风电场实际可发功率大于预测功率的概率较大，具有相似置信区间的风电场记为Ω+；部分风电场的预测功率与置信区间的上边界十分接近，表明该风电场实际可发功率小于预测功率的概率较大，具有相似置信区间的风电场记为Ω-。

2 功率预测误差对有功控制的影响

通常在风电场预测功率大于发电计划时，才对风电场有功功率进行控制。风电场i的有功控制需求ΔPi由预测功率和发电计划确定:

ΔPi=Pd,i-Pf,i

(5)

式中：Pd,i和Pf,i分别为风电场i的发电计划和预测功率。

在实施风电场有功控制时，Ω+类风电场承担的有功调节量为ΔP+，Ω-类风电场承担的有功调节量为ΔP-。

Ω+类风电场i的输出功率Pi+应为

(6)

式中：Pf,i+和PN,i+分别为Ω+类风电场i的预测功率和装机容量。

Ω-类风电场i的输出功率Pi-应为

(7)

式中：Pf,i-和PN,i-分别为Ω-类风电场j的预测功率和装机容量。

在实际运行时，Ω+类风电场的输出功率大概率能够满足控制目标，而Ω-类风电场的输出功率大概率低于控制目标，将会导致风电场群的有功功率控制无法满足调度指令。

3 风电有功控制策略

3.1 基本流程

本文根据历史功率预测误差数据统计分析误差分布特性，采用1.2节的方法建立预测功率的置信评估模型；在此基础上，结合超短期功率预测数据，给定期望的置信水平评估各风电场的预测功率置信区间，将预测功率曲线修正为预测功率带，则风电场的出力应处于该预测功率带内。为了尽可能降低由于风电功率预测误差引起的控制误差而导致经济损失，将评估得到的预测功率置信区间作为约束，从而给出有功控制模型将超短期功率预测数据和调度指令作为输入，通过优化得到各风电场的有功控制指令。具体流程如图1所示。

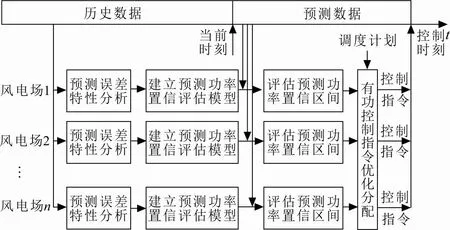
图 1 风电有功控制流程

3.2 风电有功控制模型

根据风电功率预测误差分布特性可以分析计算得到不同风电场的功率预测误差期望，进而得到功率预测期望PE,i为

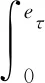
(8)

式中：Pf,i为风电场i的预测功率；Fi(e)为风电场i的功率预测误差概率分布函数。

风电场有功功率与预测功率的差值最小作为目标，目标函数为

minf=|∑(Pi-PE，i)|

(9)

约束条件为

(10)

式中：Pi为风电场i的输出功率指令。

第一个约束要求所有风电场的有功功率需要与发电计划保持一致；第二个约束为风电场运行约束。

4 算例分析

4.1 算例概述

本文以国内某省风电基地内5个风电场(总装机容量1 104 MW)2011年1—7月的预测功率和理论还原后的实测功率数据为基础，对比验证本文方法的控制效果。其中，将部分数据用于分析风电场的预测功率分布特性，将剩余的数据用于对比验证所提策略的效果。图2为风电场的预测功率、实测功率和发电指令。

图 2 风电和调度数据

5个风电场的装机容量分别为1#风电场201 MW，2#风电场201 MW，3#风电场300 MW，4#风电场201 MW，5#风电场201 MW。图3给出部分风电场当日对应时段内的预测功率和理论还原后的实测功率。

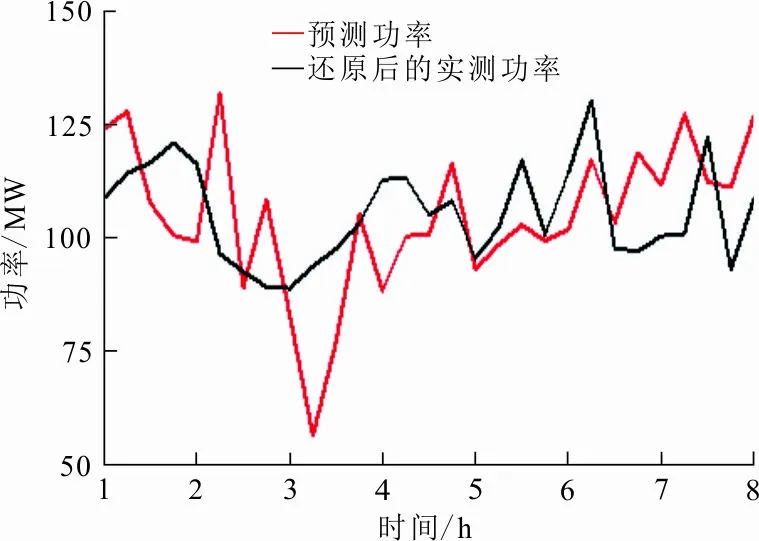
(a) 1#风电场

从图3可以看出，1#风电场的实测功率与预测功率较为接近，2#风电场的实际发电能力优于预测功率，4#风电场的实际发电能力低于预测功率。进一步设置信水平为0.95，提取各风电场预测功率的置信区间，可知风电场1#的正负误差区间较为对称，2#风电场呈现正误差特性，4#风电场呈现负误差特性。在此边界下，本算例将所提优化算法与容量比例分配方法进行对比，分析其控制效果。

4.2 考虑功率预测误差后的控制效果分析

本文所提方法的控制效果与传统容量比例分配方法的控制效果对比如图4所示。图5为部分风电场的有功控制目标与理论还原功率。

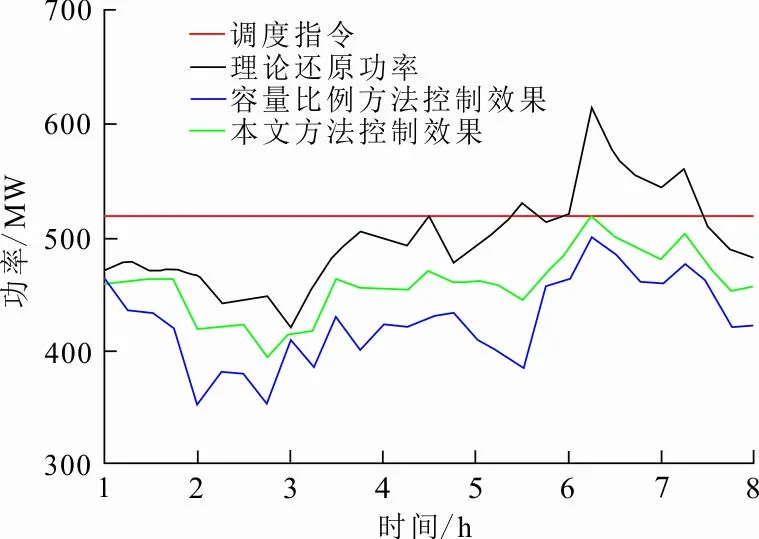
(a) 实际控制效果

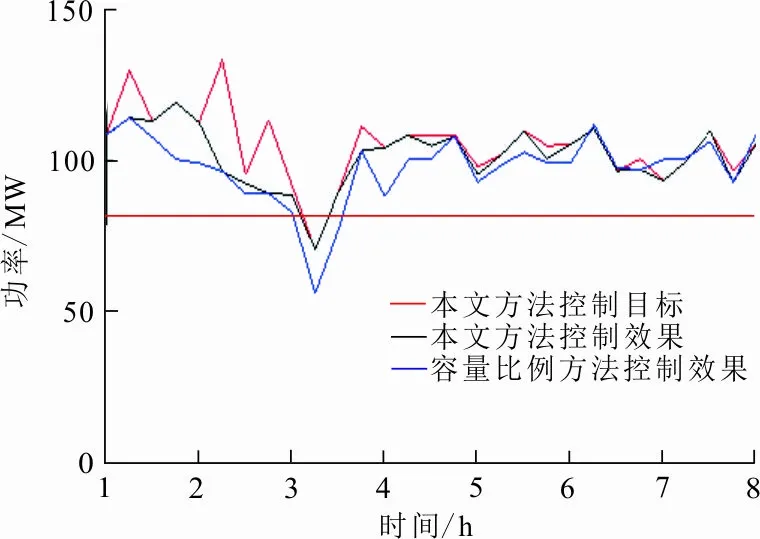
(a) 1#风电场

从图4可以看出，本文方法得到的控制目标更准确，整体控制偏差显著优于传统的容量比例分配方法。此外，相比于现有考虑误差的控制方法，本文通过历史数据的统计分析，根据正负误差特性对风电场分类，分析风电场预测功率的置信度；应用时，以风电场预测功率为输入，评估预测功率的置信区间及期望功率，优化生成风电场的功率控制指令。

从图5可以看出，由于风电场4#呈现负误差特性，无法满足控制目标的概率大，将其可能产生的功率缺额转移至风电场1#和2#。图5(a)～(c)给出了风电场1#、2#和4#的控制目标值，可见3个风电场的控制目标优于容量比例方法的控制目标，经对比发现，控制偏差可减小10%，且采用容量比例方法无法满足发电计划。

5 结 语

不同风力发电站功率预测误差分布特性存在差异，需充分考虑其差异优化完善风电场有功功率控制。通过对风电场历史数据统计分析，提取风电场预测误差分布特性并对风电场的有功控制进行合理优化。该方法能够有效降低新能源功率预测误差对功率控制的影响，提高了风电有功控制的合理性和准确性。