基于能量评估的弹载磁强计校准方法

闫小龙，于天鹏，范 旭，朱宜家，陈国光，田晓丽

(1.中北大学，太原 030051； 2.淮海工业集团， 山西 长治 046000； 3.中国兵器工业第五九研究所， 重庆 400039)

1 引言

在制导弹箭的飞行过程中，弹体姿态的快速准确测量直接决定了制导控制的精准程度，而弹箭往往又存在大过载、宽范围滚转等特性。磁强计以抗过载能力强、无初始对需求、无累计误差、体积小、重量轻、成本低等优点成为制导弹箭姿态测量的最佳选择方案[1-5]。

磁强计通常捷联于弹体，依据完善的当地地磁场信息得出磁强计各敏感轴的分量，从而获取弹体姿态[6]。但是，由于磁强计制造工艺、电路贴装工艺、获取信号的调理电路等问题，磁强计的测量输出值会受到不同因素的影响，比如磁强计敏感轴的非正交误差、比例因子误差、基线偏置误差等，这些误差都会对弹体的测量带来不同程度的偏差[7-9]。因此，在正确的测量弹体姿态前必须对磁强计进行校准，以确保测量结果的准确。在磁强计测姿的研究历程中，极大极小值校正法、椭圆/椭球校正法、递推最小二乘的罗差校正法以及基于无磁转台的误差分离标定法是最常见的校准方法[10-12]，随着磁强计在制导弹箭领域的运用，一些自适应的在线校正滤波方法也不断被提出，比如非线性的卡尔曼滤波方法(EKF、UKF)等[13]。这些方法都有着不错的校准效果，但是针对弹箭使用的磁强计测姿系统来说，磁强计在发射初期非常容易受到各种铁磁物质的干扰，且全弹道时长又相对较短。因此，如何快速准确的对弹载磁强计测姿系统进行在线校准是一个非常具有挑战性的问题[14-15]。

本文旨在提出一种针对旋转弹体的磁强计在线校准测量方案。在弹箭发射后对弹体捷联磁强计获取的数据在时域内进行基于能量的初始概略评估，快速获取磁强计校准参数初始估计值后，将弹体的滚转姿态二阶拟合参数与磁强计校准参数一同作为无迹卡尔曼滤波器的状态量初值，在快速得到弹体滚转姿态信息的同时进一步对磁强计校准参数进行精准获取，为了保证弹体姿态的求解效率，在判定磁强计校准参数收敛稳定后对无迹卡尔曼滤波器进行简化重构，极大地降低姿态信息求解的空间及时间复杂度。所提出的算法将有效的提高磁强计校准精度及姿态求解速度。

2 磁强计测姿误差模型

将磁强计捷联于旋转弹体后，由于磁强计本身的制造工艺误差、调理电路封装误差、磁强计相对弹体安装误差以及弹体干扰等原因使得磁强计获取的磁场信息与当地磁场信息不符，误差模型可以描述为

(1)

图1是基于磁强计的角度测量模型。图1中Ox′、Oy′、Oz′分别为弹体的x、y、z轴，其中Ox′方向为弹箭头部指向，Ox、Oy、Oz分别为捷联磁强计的x、y、z轴，为了在可行的操作范围内降低磁强计的校准难度，在磁强计安装于弹体时认为弹体y轴与磁强计y′轴是重合的。其中δz为磁强计z轴与弹体z′轴的误差角，δxz为磁强计x轴与弹体x′y′平面的误差夹角，δxy为磁强计x轴在弹体x′y′平面的投影与弹体x′轴的误差夹角。

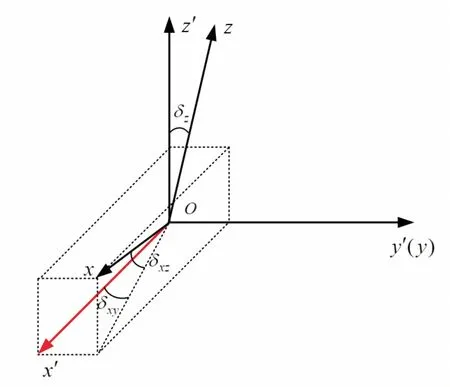
图1 捷联磁强计非正交误差模型示意图Fig.1 Magnetorometer non-fixed error model

因此，可以磁强计的非正交误差矩阵可以描述为

(2)

结合磁强计误差模型，并且忽略软铁误差与噪声的前提下，对于旋转制导弹箭的三轴磁强计输出模型可以表示为

(3)

式中:sx、sy、sz分别为三通道敏感轴的比例因子；Bbx、Bby、Bbz分别为三通道敏感轴的偏置误差；Bex、Bey、Bez分别为地磁场be在弹体三轴方向上磁分量；ω为弹体飞行滚转角速度；t为飞行时间；By、Bz为磁强计弹体横截面内两敏感轴的输出值；φ0为磁强计的初始相位角。

则式(3)可以描述为

(4)

依据磁强计与弹体捷联关系，求解上式可得弹体实时滚转姿态角：

(5)

式中：sy、sz、Bbz、Bby、δz为磁强计待校准参数值。

通常情况下，在弹箭发射及飞行过程中，如果不对滚转姿态进行控制，则滚转运动可以近似的认为是匀加速的，且加速度是非常小的，因此滚转运动可以近似的描述为。

(6)

式中：Φ0为弹箭的初始角位移；Φ′为弹箭的滚转角速度；Φ″为弹箭的滚转角加速度。表达式中“i”表示第i个采样周期对应的数据。

在弹道的参数处理过程中，通常通过实时滤波的方法将参数估计的问题转换成参数实时滤波的问题，从而增加参数的时效性与准确性。在此建立滤波的系统状态方程与量测方程：

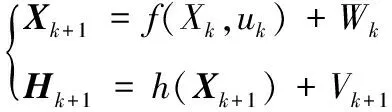
(7)

式中：Xk+1为系统状态向量；f(Xk，uk)为系统线性函数；h(Xk+1)为系统的非线性函数；Wk为系统方程高斯白噪声；uk为确定性控制向量；Hk+1为系统的量测向量；Vk+1为测量方程的高斯白噪声。

3 基于磁强计能量捕获的校准参数估计

3.1 磁强计能量捕获

在利用磁强计测量弹体飞行滚转姿态前，磁强计必须进过精确校准才能准确获取弹体滚转角。由式(4)可知，磁强计的校准参数均包含在磁强计敏感轴测量模型中。依据磁强计测量磁场机理，磁强计敏感轴敏感当地磁场在轴上的分量，并以模拟量或数字量的形式输出，其本质反应的是当地磁场在轴方向上的分量。当旋转弹体在飞行过程中，弹体绕弹轴旋转，其捷联在弹体上的磁强计y轴与z轴敏感到固定磁场的磁分量为正弦变化的。因此，依据获取参数对两个敏感轴的磁能曲线进行拟合，可以快速的得到磁强计校准参数的初始估计值。y轴与z轴的实时磁分量可以描述为

(8)

根据法拉第电磁感应产生的电动势可知：

(9)

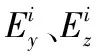
针对制导弹箭来说，一般发射过程会赋予弹体一个预设的角速度，这个角速度通常由身管膛线或发射架体的导转机构来确定的，因此弹体的初始角速度可以描述为

(10)

式中:vi为弹体在身管内的移动速度、r为身管半径，θ为身管缠线角。

依据磁场能量模型，结合式(8)～式(10)可得ti时刻由于磁场变化产生的能量可以表示为

(11)

式中，k为能量与磁场强度的修正系数。

3.2 磁强计校准参数估计

由式(11)可以看出弹体捷联磁强计两个正交的敏感轴捕获磁场能量可以描述为正弦与余弦的函数关系，依据磁强计的实时采样值与弹体炮口初速估计值对两敏感轴磁能模型进行三角函数拟合。

令：

(12)

则有

(13)

(14)

求解上式即可得到Ay、Φy、Ky、Az、Φz、Kz的最优拟合值，结合式(12)即可求得磁强计在弹体截面内两个敏感轴的校准参数初值sy、sz、Bby、Bbz、δz。

4 二次重构无迹卡尔曼滤波算法求解弹体滚转姿态

当获取到磁强计的校准参数后，由式(5)可计算出弹体的滚转姿态角，因此，状态向量初值为

列出无迹卡尔曼滤波器方程：

(15)

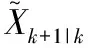
更新状态矩阵和协方差矩阵：

(16)

(17)

鉴于校准参数的最优估计结果间存在耦合关系，将误差估计定义为

(18)

式中，S是磁强计校准参数的真实值。

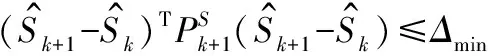
(19)

5 数值仿真

为了验证算法的有效性，对该算法进行数值仿真。建立弹体捷联磁强计测量模型，并人为设置仿真误差参数：Y敏感轴Bby误差设置为1.4%，比例因子误差设置为6%，Z敏感轴Bbz误差设置为4.8%，比例因子误差设置为-0.9%，非正交误差角δz设置为12°，系统噪声设置为0.2%，测量噪声设置为0.2%，采样频率为500 Hz，如图2所示。

图2 产生的预设误差样本曲线Fig.2 Produced data sample

由滤波结果可以看出从弹道时5 s开始比对结果，磁强计敏感轴Bby、Bbz校准参数最终精度在0.1‰，比例因子sy/sz校准参数最终精度在3‰，非正交误差角δz校准参数最终精度在4‰，滚转姿态角估计误差最终精度在0.23°左右，如图3～图6所示。在弹箭的闭环控制飞行中，0.23°的滚转姿态误差是非常小的，完全可以满足弹箭控制飞行需求。

图4 比例因子参数滤波结果曲线Fig.4 Scale factor parameter filtering result

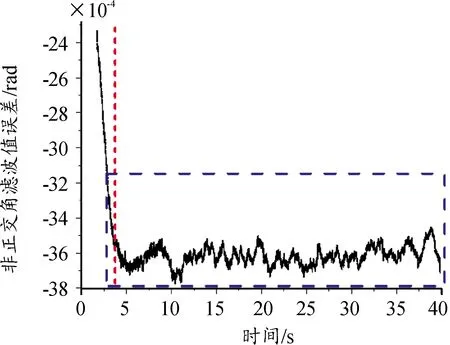
图5 非正交误差角参数滤波结果曲线Fig.5 Non-orthogonal error angular parameter filter results

图6 弹体滚转姿态角滤波结果曲线Fig.6 Military roll gesture angle filter results

6 结论

提出了一种基于能量评估的无迹卡尔曼滤波算法(PUKF)，用于弹箭飞行过程中在线快速校准磁强计并估计弹体滚转角姿态。有效地解决了旋转弹体在发射后不能及时获取滚转信息而无法进行控制的问题。与现有算法不同，所提出的算法通过磁强计敏感轴捕获的磁分量建立磁能函数，结合弹体炮口转速估计值对磁能三角函数进行参数估计。将初步获取的校准参数估计值与磁强计测量值对弹体滚转姿态进一步解算，最终将磁强计校准参数、弹体滚转姿态一起作为无迹卡尔曼的滤波初值进行滤波处理，获取精确的磁强计校准参数与弹体滚转姿态角信息。通过校准参数的三角函数拟合处理与无迹卡尔曼滤波算法相结合有效的减少了滤波收敛时间，使得弹箭出炮口较短时间内较准确的获取弹体滚转姿态用于航迹控制，提高了弹箭的作战效能。