压缩感知中测量矩阵筛选的等值线图和优化的适用性
2022-01-10吴小龙李德高
吴小龙,程 涛,李德高,吴 艳
(广西科技大学 a.机械与交通工程学院; b.电气与信息工程学院, 广西 柳州 545006)
1 引言
对于稀疏信号,压缩感知(compressive sensing,CS)可以在特定的条件下对信号进行采集的同时对其压缩,并以比奈奎斯特采样定理低得多的采样频率进行高质量的信号重构[1-4]。CS的数学模型如式(1)所示:
min ‖x‖0s.t.y=Φx
(1)
其中,y是测量数据,y∈RM;Φ是测量矩阵,Φ∈RM×N,M CS的约束等距特性(restricted isometry property,RIP)如式(2)所示: (1-σK)‖x‖2≤‖Φx‖2≤(1+σK)‖x‖2 (2) 其中σK∈[0,1)。 测量矩阵满足RIP准则是实现压缩采样信号有效重构的关键,但是判断测量矩阵是否满足RIP很难。因而RIP缺乏实用性和可用性[7]。当前判断测量矩阵性能的主要判据是测量矩阵列间相关系数绝对值的最大值(μcmax),如式(3)所示: (3) 其中,Φi和Φj分别是测量矩阵的第i和j列。测量矩阵的μcmax越小,其性能越好。从而在重构过程中可以获得更好的重构效果[8]。 压缩感知中测量矩阵的设计、优化和性能是关系信号重构的关键因素。高斯矩阵、0-1随机矩阵(简称为随机矩阵)与0-1循环矩阵(简称为循环矩阵)是在压缩感知研究和应用中广泛使用的3种测量矩阵[1,5,9]。高斯矩阵虽然具有好的RIP、信号重构能力和普适性,但难以硬件实现。随机矩阵和循环矩阵都易于通过数字微镜(digital micromirror device,DMD)实现。循环矩阵在硬件实现和编程设计方面比随机矩阵更有优势。尽管随机矩阵和循环矩阵的列不相关性差,但通过测量矩阵的优化算法可以极大改善和提高测量矩阵的列不相关性,从而获得不弱于高斯矩阵的信号重构效果[7-8]。 矩阵优化设计的准则主要是列间相关性最小化[10-12]。Elad和Duarte[11-12]以列间相关性最小化为目标进行矩阵优化。尽管取得了较好的优化效果,但存在方法复杂、操作不便的弊端,而且是非直接优化。对测量矩阵Φ做各行正交规范化处理后,可得到优化矩阵ΦO,优化矩阵的性能好于测量矩阵。通过优化矩阵可求得过渡矩阵T=ΦOΦT(ΦΦT)-1以及近似矩阵ΦT[7-8]。在重构阶段以测量阶段的测量数据,通过式(4)可重构得到更好的重构效果[7-8]。 min‖x‖0s.t.yT=ΦTx (4) 其中yT=Τy,ΦT=ΤΦ。 256是小压缩比(测量矩阵的列数与行数之比)压缩感知研究中常用的测量矩阵列数[7-8,13];4 096是大压缩比压缩感知研究中常用的测量矩阵列数[14-17]。如何从优化设计角度选择合适大小的测量矩阵缺少相关研究。因此,本文基于列不相关性,研究了不同压缩比的最大列数为256和 4 096的随机矩阵、循环矩阵与高斯矩阵,为测量矩阵优化提供指引和方向,避免压缩感知中测量矩阵选择的盲目性。 为构建筛选测量矩阵的依据,分别研究最大列数为256和4 096的随机矩阵、循环矩阵与高斯矩阵优化前后的性能变化,并总结其分布规律。 随机矩阵和循环矩阵中每行随机分布k个1,k=N×13/36 (如k不为整数,则取小于该数的最大整数),除1外其它元素均为0。循环矩阵中各行向量都是前一行向量各元素依次右移2位的结果。k=N×13/36是经过大量筛选实验获得的经验值。它能较好满足同一矩阵中不出现相同行或列,而且1的数量尽量少的要求。 总之,天然林的生态功能和经济效益是现在人工林所不能替代的。天然更新的能力巨大,更新的面积和株数远远大于同期人工更新的面积和株数。对此,可以实行人工更新与天然更新相结合的方法,即又节约人财物力,节约时间,又能保证更新成活率,同时又可培育优良的“人天”混合林。 图1 最大列数为256的随机矩阵优化前后及其差值的等值线图Fig.1 Contour map of and its difference before and after optimization of a random matrix with a maximum number of 256 columns 图2 最大列数为4 096的随机矩阵优化前后及其差值的等值线图Fig.2 Contour map of and its difference before and after optimization of a random matrix with a maximum number of 4 096 图3 最大列数为256的循环矩阵优化前后及其差值的等值线图Fig.3 Contour map of and its difference before and after optimization of the circulant matrix with the maximum number of columns of 256 图4 最大列数为4 096的循环矩阵优化前后及其差值的等值线图Fig.4 Contour map of and its difference before and after optimization of the circulant matrix with the maximum number of columns of 4 096 图5 最大列数为256的高斯矩阵优化前后及其差值的等值线图Fig.5 The contour map of and its difference before and after optimization of the Gaussian matrix with the maximum number of columns of 256 图6 最大列数为4 096的高斯矩阵优化前后及其差值的等值线图Fig.6 The contour map of and its difference before and after optimization of the Gaussian matrix with the maximum number of columns of 4 096 当高斯矩阵列数很大时,如果行数很大,各列包含的元素很多,各列之间已经近似正交。即使对高斯矩阵优化,可优化的空间和潜力都非常有限。如果行数较少,各列包含的元素不多,样本容量不够。而列数很大,导致大概率出现列相关性较大的列。因此,图6(a)中行数小于256的高斯矩阵的等值线迅速趋近于1。这时对高斯矩阵优化,可优化的空间和潜力也非常有限。因此,测量矩阵优化适用于随机矩阵和循环矩阵和最大列数较少的高斯矩阵,不适用于最大列数很大的高斯矩阵。 128×256是各种压缩感知研究中经常采量矩阵用的测大小[7,13]。当测量矩阵列数采用4 096时,多采用超大压缩比[16]。图7和图8采用正交匹配追踪( orthogonal matching pursuit,OMP)算法[13]给出了128×256和32×4 096的随机矩阵、循环矩阵和高斯矩阵优化前后对相同信号的重构结果。信号采用高斯稀疏信号,对每个稀疏度都重复试验50次,然后计算信号的精确重构概率,仿真软件采用Matlab R2015b。 由图7可见,128×256的随机矩阵、循环矩阵和高斯矩阵优化后的曲线位于优化前的上方,重构质量和效果获得很大改善。由图8可见,32×4 096的随机矩阵和循环矩阵优化后的曲线位于优化前的上方,重构质量和效果获得较大改善。但是高斯矩阵优化前后的曲线几乎重合在一起,重构效果没有改善。 图7 128×256的3类矩阵优化前后重构概率与信号稀疏度的关系曲线Fig.7 The relationship curve between reconstruction probability and signal sparsity before and after optimization of 128×256 three types of matrices 图8 32×4 096的3类矩阵优化前后重构概率与信号稀疏度的关系曲线Fig.8 The relationship curve between reconstruction probability and signal sparsity before and after optimization of 3 types of 32×4 096 matrices 表1为128×256和32×4 096的随机矩阵、循环矩阵和高斯矩阵优化前后的μcmax及其差值。由表1可见,128×256的随机矩阵、循环矩阵和高斯矩阵优化前后的μcmax分别提高0.333、0.310和0.099。由表1可见,32×4 096的随机矩阵、循环矩阵和高斯矩阵优化前后的μcmax分别提高0.018、0.024和0.003。对图7、图8和表1综合考虑,测量矩阵优化后的μcmax提高约0.01,就能获得明显的重构效果改善。32×4 096的高斯矩阵优化后的μcmax仅提高约0.003,因此导致重构效果无改善。 表1 3类矩阵优化前后μcmax及其差值2 测量矩阵的等值线图和理论分析
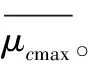


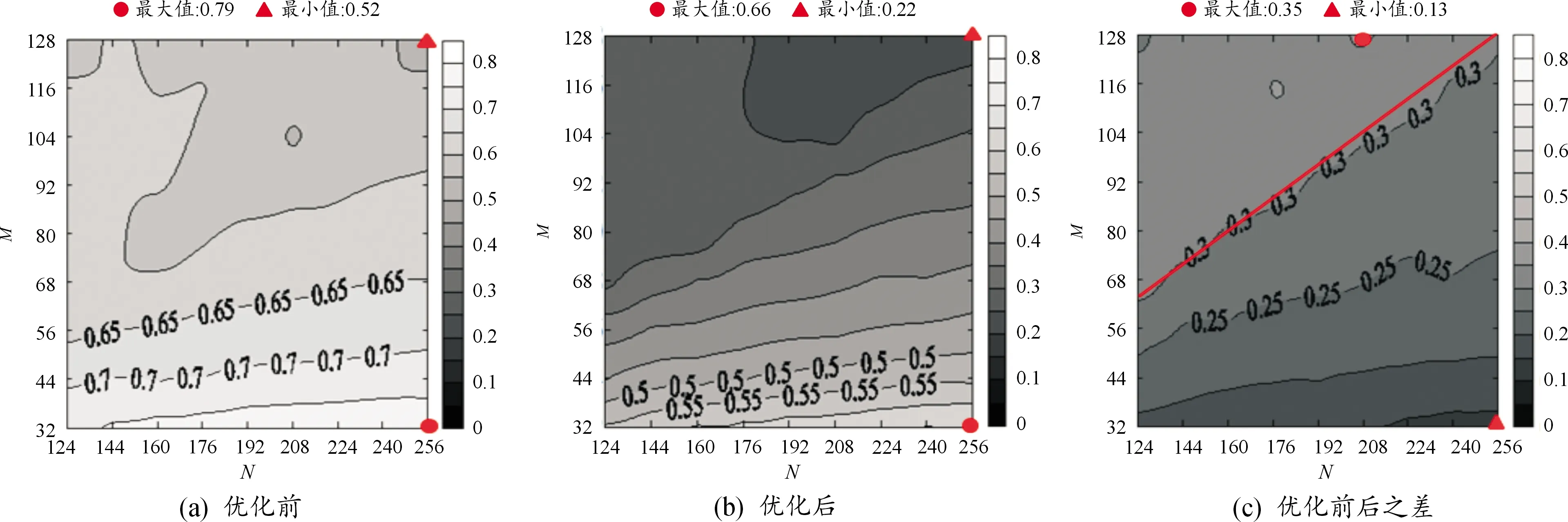



3 信号重构结果对比和验证



4 结论

