基于相位补偿的外辐射源雷达旋翼目标特征提取

周子铂 张朝伟 夏赛强 许道明 高 妍 曾晓双

①(空军预警学院 武汉 430019)

②(中国人民解放军31001部队 北京 100095)

1 引言

鉴于全球定位导航系统(Global Navigation Satellite System,GNSS)广泛的覆盖率和稳定的工作性能，利用GNSS信号进行目标探测与识别的应用已经引起广泛研究。该型外辐射源雷达无发射机，信号源自空间轨道上的定位导航卫星，而接收机位于地面，属收发分置雷达系统[1,2]。在目标散射方面具备雷达散射截面增强的特性，即前向散射增强，所以前向散射系数远高于后向散射系数[3]。此散射特性促使外辐射源雷达在处理GNSS辐射的低功率信号时具备相当的可行性，尤其在近空域目标识别应用之中[4,5]。

不同于目标整体的平动，旋翼叶片的旋转运动被称为“微动”[6]。目标的微动导致雷达接收回波中除了含有平动多普勒频率之外，还包含有“微多普勒”频率[7,8]。而微多普勒频率的大小和变化趋势与旋翼目标的特征密切相关，不同的旋翼目标具有自身独特的微多普勒效应[9—11]，因此可以利用雷达回波的微多普勒效应提取目标旋翼特征参数。

文献[12]推导了基于GNSS外辐射源的直升机旋翼目标回波理论模型，详细分析了微多普勒特性分析对于外辐射源的系统要求，并结合几种典型直升机的参数特征给出了不同观测视角下所能达到的作用距离，以及回波信号的信干噪比。此外，Carmine.C等人还利用时频工具获取了典型直升机模型的时频分布。基于单基地模型，朱名烁和陈永彬在文献[13,14]中分析了叶片上散射点的不同分布情况和目标不同的姿态角对回波的影响，并在此基础上研究了时域闪烁现象的物理形成机理，但是未进一步提出具体的旋翼目标参数提取方法。针对微多普勒效应分析问题，文献[15]根据转动部件的周期性旋转导致微多普勒频率呈正弦变化的特点，提出利用霍夫变换检测时频图谱中的微动曲线，进而实现目标参数特征的提取。文献[16]提出利用正交匹配追踪(Orthogonal Match Pursuit,OMP)算法在电视广播信号做辐射源的条件下对旋翼直升机目标进行参数估计，但是匹配追踪这类贪婪算法搜索到的可能是局域内的极值，而非全域的最值，因此会降低算法的稳定性。张群等在文献[17]中研究了频分复用模式下基于多重观测矢量模型和系数重构方法，该方法可以实现较高的参数估计精度，但是所要求的数据量将随着模型重数上升而显著增加。

旋翼叶片的周期性旋转引起回波的周期性调制，当叶片旋转到形成镜面反射的角度时，回波在时域形成峰值闪烁，非镜面反射时则呈现为波谷，因此时域回波呈现为间隔一定时间出现的谱峰。在时频域内，该闪烁表现为占据一定带宽的频率带，并且频率带的相对位置关系与旋翼结构的转动参数密切相关。目前常用的参数提取算法主要是根据谱峰间隔与叶片数量和转速的关系，以及最大微多普勒频率与叶片尺寸与转速的关系实现。然而，本文考虑从闪烁位置变化的角度进行旋翼参数估计，然后在时频图谱中直接得到旋翼叶片数量。针对外辐射源旋翼参数估计问题，本文首先分析时频域闪烁分布的数学形成机理，然后根据回波相位项导致时频域闪烁呈现起伏的特征，提出利用相位补偿的方法完成同一叶片闪烁的零频聚焦。最终，在时频图谱中直接获得旋翼目标包含的叶片数，然后根据闪烁中心频率距离基准频率最近的原则估计其他参数。另外，本方法利用最佳相位补偿之后的时频图谱还可以实现旋翼目标在回波域的叶片分离。

2 GNSS外辐射源雷达旋翼目标微动模型

2.1 外辐射源雷达旋翼目标探测模型

图1(a)所示为外辐射源雷达的目标探测模型，外辐射源雷达通常设置有两个接收通道，观测通道接收目标反射回波，参考通道则主要用于接收直达波。针对GNSS信号为连续波(周期Tp1 ms，码片速率为1.023 Mbits/s)的特点，此处考虑采集时长为Tp的信号片段构成一个脉冲，然后对采集的多个脉冲进行相干处理。图1(a)中R0,Rt和Rr分别表示卫星到接收机的直达距离、双基地雷达发射距离和接收距离，双基地角为β，波长为λ。设旋翼目标的叶片旋转速率为fr，相应的旋转角速度为w，且与角平分线夹角为φ，如图1(b)所示。则接收回波与直达波信号匹配滤波之后可表示为

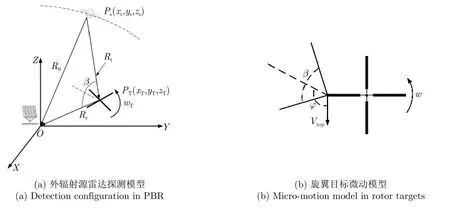
图1 外辐射源雷达旋翼目标微动模型Fig.1 Micro-motion model of rotor targets in PBR

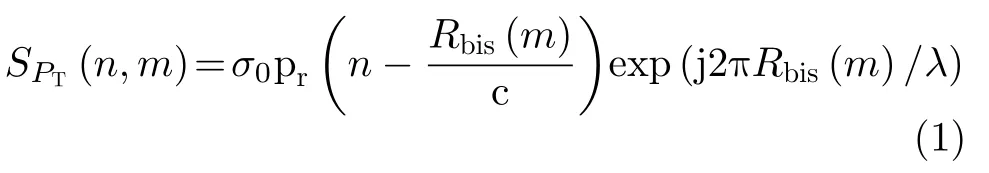
其中，σ0为回波幅度，Rbis(m)为双站距离。pr(n,m)表示匹配滤波之后包络函数。

2.2 旋翼目标微动模型

本文设定外辐射源地杂波和机身回波已利用经典算法进行抑制，例如扩展相消算法[1]、自适应复变分模态分解[18]、经验模态分解[19]等，回波信号只剩下目标旋翼回波以及噪声。以旋翼直升机为例进行讨论，并考虑目标处于悬停状态，式(1)中双站距离Rbis(m)可建模为

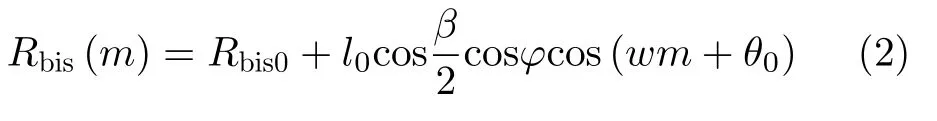
其中，Rbis0为旋转中心的双基地距离，l0表示散射点距旋转中心的距离，叶片总长度为L，该叶片初始角为θ0。cos(β/2)cosφ可称为双基地因子，主要由目标与雷达系统的相对位置决定，此处设定已完成目标定位，并且已完成目标平动补偿。

根据文献[12]可推导外辐射源条件下单叶片的回波模型为

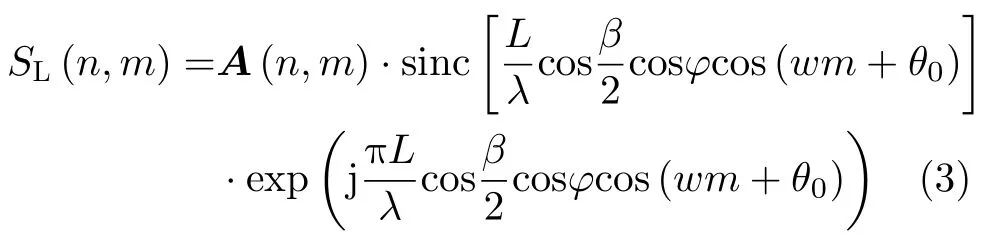
其中，A(n,m)表示接收信号包络幅度及与微动无关的平动相位。

设旋翼目标共有Q个叶片，则该旋翼目标的回波信号可建模为

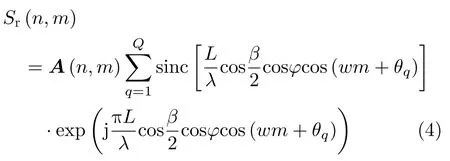
那么，第q个叶片旋转运动引起的微多普勒频率为

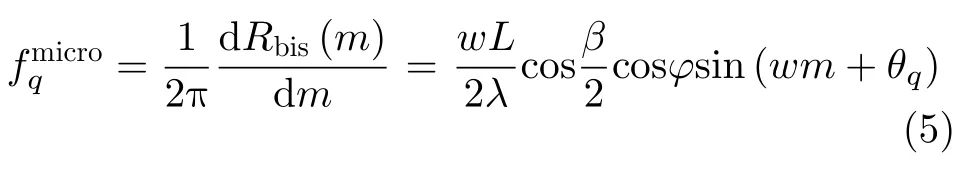
式(5)表明目标回波信号微多普勒频率在慢时间域受正弦函数sin(wm+θq)的调制，即微多普勒频率是随慢时间呈非线性变化的。另外，式(5)表明微多普勒频率的最大值由目标旋翼的长度、转速、波长以及目标所处的双基地位置共同决定。当其中相位项φwm+θq满足式(6)时，多普勒频率呈现最大值，且最大值如式(7)所示，为该旋翼目标的最大微动多普勒频率。另外，结合式(4)和辛克函数的特点，此时辛克函数出现极值，即在慢时间域出现闪烁。

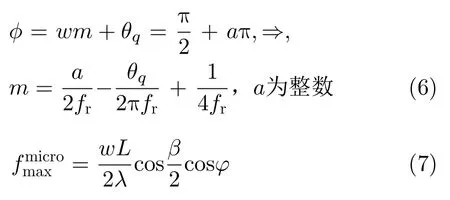
3 基于相位补偿的旋翼目标微动特征提取

3.1 旋翼目标回波时频分析

仔细考察式(4)，忽略回波振幅的影响，单个叶片的回波主要由辛克函数与相位的乘积构成。不失一般性，第1个叶片的回波可简写为

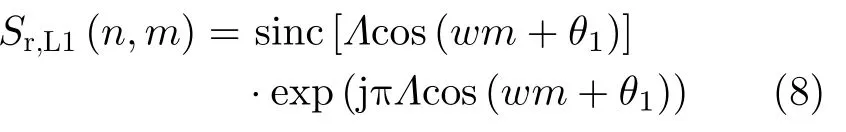
由式(5)和式(8)可见，单个叶片的回波呈现为多个辛克函数求和的形式，且回波多普勒频率是时变的，所以此处考虑采用短时傅里叶变换(Short Time Fourier Transform,STFT)在慢时间维对回波的多普勒频率进行分析。由傅里叶变换的性质可知：

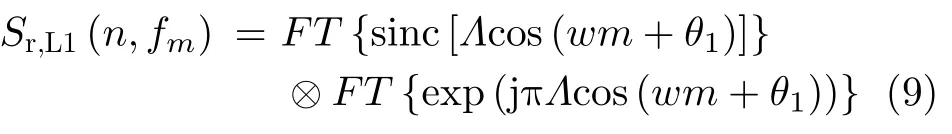
其中，FT{ }表示傅里叶变换。鉴于sinc(t)与rect(f)为一对傅里叶变换对，且指数函数的傅里叶变换易于求解，具体如式(10)和式(11)所示：

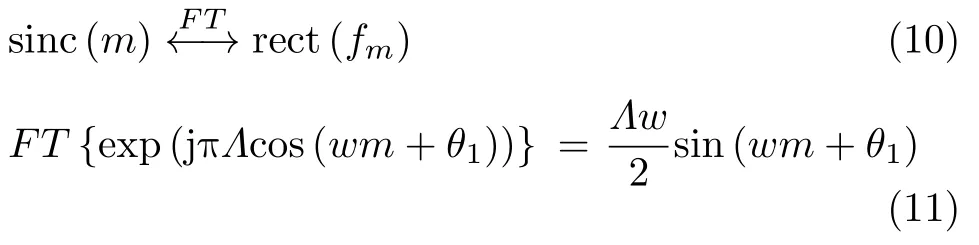
可见，回波包络的傅里叶变换为占据一定带宽的矩形条带函数，在时频图谱中为闪烁条带，如图2(a)所示；而相位的傅里叶变换为一段正弦函数，如图2(b)所示。

由式(9)可知，单叶片回波的傅里叶变换为包络的傅里叶变换与相位傅里叶变换的卷积，进而可得完整回波信号的时频图谱如图2(c)所示。这就是旋翼叶片回波在时频域呈现随慢时间起伏的闪烁条带的数学形成机理。因此，如果将该叶片回波中的相位补偿完全，对应叶片的时频图谱将由图2(c)变成图2(a)，即完成该叶片的相位补偿，这样便可在多个叶片产生的多次闪烁当中将完成相位补偿的叶片识别并提取出来，且聚焦到零频的闪烁属于相同的叶片，根据两个零频闪烁间隔的闪烁数量估计整个旋翼的叶片数。

3.2 相位补偿算法

根据式(8)，建立回波的补偿相位：

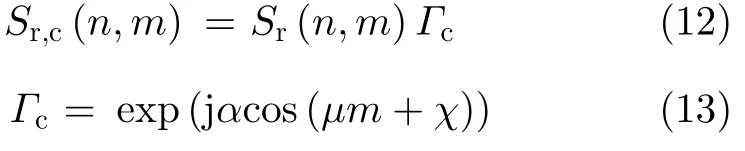
其中，α,µ,χ分别表示幅度、角速度与初相的系数向量，这样就将旋翼参数估计问题转换成最优化求解问题了。根据3.1节所述，单叶片回波经过相位补偿之后的时频分布为一系列中心频率为零的零频闪烁，下面详细分析不同旋翼结构下的基准频率。

3.2.1 非对称结构相位补偿

当目标旋翼包含有奇数叶片时，由于叶片的不对称性，时频域正负频率闪烁交替出现，其时频分布类似图2(c)。鉴于回波相位的参数Λ与的关系Λ即参数α与µ相关联。设fCD表示单叶片闪烁条带的带宽，则fCD因此参数搜索维度就由三维变换到二维 (µ,χ)。进一步推导，可将式(12)重写为

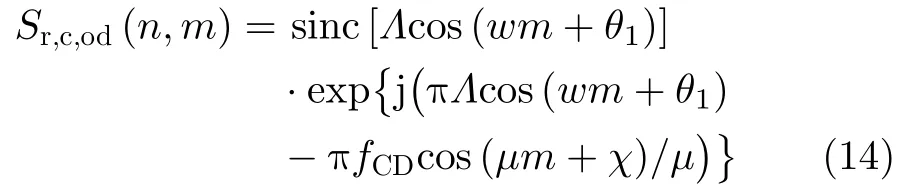
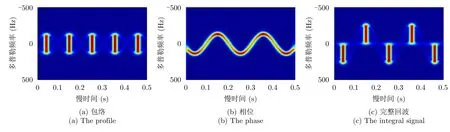
图2 单个叶片的时频图谱Fig.2 The TFD of signal blade

仔细考察相位项发现，其正相关于两个正弦函数的差值，并且差值的变化趋势与参数 (µ,χ)相关。具体分以下3种情况讨论：

(1) 当wµ,θ1χ时，该叶片回波相位被补偿完全，此时：

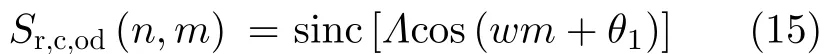
(2) 当wµ,θ1̸χ时，剩余相位为两个同频但初相不等的正弦信号的差值，变化趋势与正弦信号相同：

(3) 当w ̸µ,θ1χ时，剩余相位为两个不同频的正弦信号之间的差值，在时间域呈现为幅度逐渐变化的振荡：

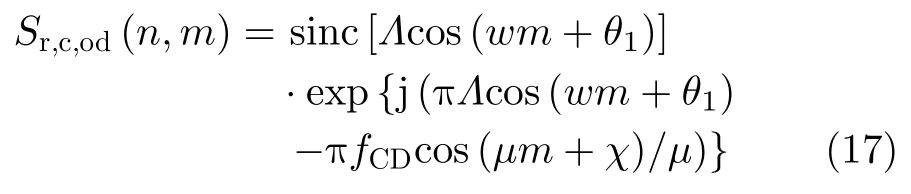
为充分说明上述不同情况下的回波多普勒频率的变化情况，分别设置不同参数，计算剩余相位exp{j2π(cos(wm+θ1)−cos(µm+χ))}的多普勒频率，其波形如图3所示。

图3(a)中黑色虚线是wµ4.8×2π,θ1−χ=π/9时的结果，可见当正弦函数角频率w相同时，两个正弦函数的差值依然是正弦函数，因此剩余相位的多普勒频率依然被正弦函数调制，时频图谱中的闪烁也无法聚焦到零频。图3(b)中红线表示相位补偿完全情况下的多普勒频率，可见多普勒频率恒等于零。黑色虚线表示w4.8×2π,µ4×2π,θ1χ时的计算结果，可见不同频正弦函数的相位补偿将导致多普勒频率随时间变化，且变化趋势为幅度变化的振荡。因此，不同频的补偿相位无法将回波相位补偿完全，时频图谱上相同叶片的全部闪烁无法聚焦到零多普勒频率。

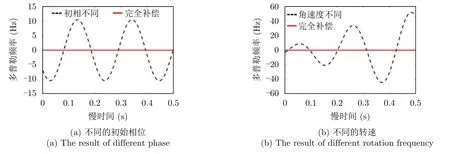
图3 不同正弦函数差值导数波形图Fig.3 The result of different sinusoidal function

综上，第1种情况多普勒频率始终为零频，第2种情况多普勒频率呈现为规律的正弦变化曲线，第3种情况下同样未形成聚焦，表现为幅度不断变化的不规则振荡。因此，仅在相位补偿完全的条件下，非对称结构旋翼目标闪烁的基准频率为零。

3.2.2 对称结构相位补偿

当目标旋翼包含有偶数叶片时，由于叶片的对称性，时频域内同一时间会出现正频率闪烁和负频率闪烁。其中，正频率闪烁表示闪烁条带中心频率为正值，负频率闪烁的中心频率则为负值。

进一步，两个对称叶片的回波可简写为

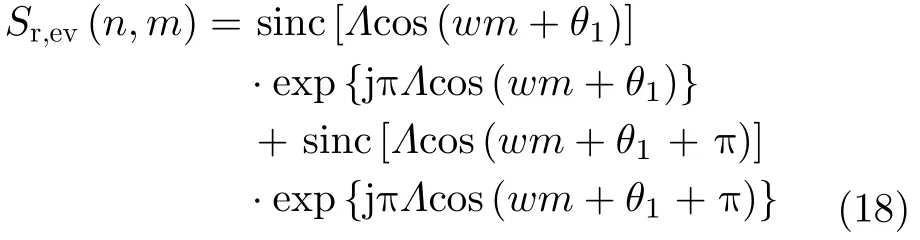
那么，相位补偿之后的回波可表示为

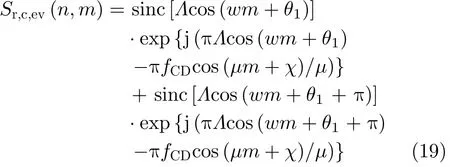
仔细考察式(19)可以发现，由于两个叶片的初始相位不同，无法同时完成两个叶片的相位补偿，所以对称结构旋翼回波闪烁无法聚焦到零频。当w ̸µ或θ1̸χ时，相位补偿情况如上一节所述，因此本部分主要讨论最佳补偿情况。当wµ,θ1χ时，式(19)可推导为

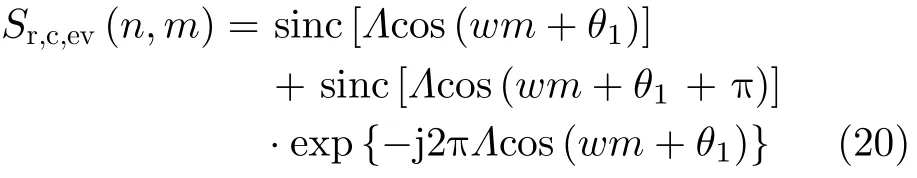
由式(20)可知，在产生闪烁的时间，两个对称的叶片分别产生零频闪烁和非零频闪烁。具体后者的多普勒频率如式(21)所示。

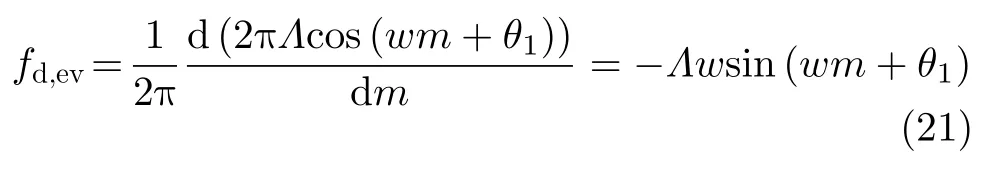
根据式(21)可知，后者的多普勒频率呈现正弦变化的趋势，因此后者产生闪烁的中心频率也成正弦函数起伏。考虑到该叶片对的闪烁恰好出现在同一时刻，在时频图谱上表现为同一时刻连接在一起的双闪烁。其中一个叶片的相位被补偿完全，该叶片的回波只剩慢时间域包络，时频图谱中的闪烁被聚焦到零频附近。另一个叶片的相位变为原来的负二次方，其聚焦的多普勒频率变为。显然，该叶片对形成的闪烁连接在一起构成双闪烁，且该双闪烁的中心频率位于处。

总体而言，该时刻双闪烁的频率带宽为单闪烁的两倍，并且中心频率由零变成振幅为Λw的正弦函数。当该对称叶片旋转半圈之后，即相位增加π，闪烁的中心频率则由−Λw变化到Λw，然后再次变化到−Λw。虽然此时闪烁的中心频率随时间变化不定，但同一对称叶片产生双闪烁的中心频率仅仅出现Λw和−Λw两种结果。因此仍然可以将时频域闪烁条带的中心频率聚焦到确定值，此处选择基准频率为负值−Λw。

3.3 参数提取最优化准则

针对上述分析，为克服剩余相位多普勒频率的不规则振荡并减弱单个闪烁聚焦效果的不稳定性引起的估计误差，此处考虑利用回波时间内单叶片或者对称叶片对的所有闪烁进行最优化参数搜索。另外，此处假设同一旋翼目标的所有叶片转速相同，差别仅在于各叶片的初相。因此，获得其中一个叶片参数即可获得整个旋翼的相关参数，所以本算法考虑利用单个叶片或者叶片对的相位补偿实现整个旋翼目标的特征提取。由于相位补偿之初无法得知哪些闪烁属于同一叶片，并且可能出现多个补偿相位使某个闪烁聚焦到相同的多普勒频率，所以此处考虑采用迭代的方式逐渐搜索到属于某一叶片的全部闪烁，并将其聚焦到零频，并以此为原则估计目标的各项参数。

当旋翼结构非对称时，基准频率为零，此时计算闪烁中心频率的绝对值即表示闪烁中心距离基准频率的频率差。起始阶段可以选择时频图谱中的任意一次闪烁作为基准闪烁([D1])，利用基准闪烁中心频率最小进行第1次迭代，搜索获得最佳补偿之后的时频图谱。然后再利用闪烁中心频率最小原则对基准闪烁进行扩展，如3.2.1节所分析。根据其余各闪烁中心频率最小的原则寻找第2个闪烁([D2])，并加入基准闪烁([D1,D2])，然后根据该两个闪烁进行第2次迭代，并完成基准闪烁的更新；如此逐渐增加基准闪烁([D1,D2,...,DI])的数量，直至剩余其他闪烁的中心频率均大于阈值。此时观测时间内该叶片所有闪烁完成聚焦，而其他叶片的闪烁未完成聚焦。最佳迭代之后的相位补偿结果在时频图谱上呈现为一系列规律的零频闪烁，然后根据两次零频闪烁之间间隔的闪烁数确定旋翼目标包含的叶片数量，并估计转速和初相。

根据式(7)可知，在获得目标的转速之后，可以根据闪烁条带的多普勒带宽估计旋翼叶片的长度。

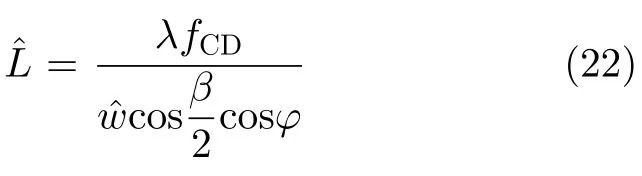
同样，当旋翼结构对称时，对称叶片产生的双闪烁基准频率为−Λw，根据上述逐步聚焦的原则，将所有应当聚焦到−Λw的双闪烁聚焦完成。此外，如3.2.2节所述，两个聚焦到−Λw处的双闪烁之间的位于Λw处的双闪烁也属于该叶片对。然后从时频图谱中直接获得旋翼叶片数，并根据整体双闪烁中心频率距离−Λw最近的原则估计该旋翼目标的其他相关参数。

综上，通过相位补偿算法，可以实现旋翼目标的特征参数提取，具体算法执行框图如图4所示，其主要步骤如下：

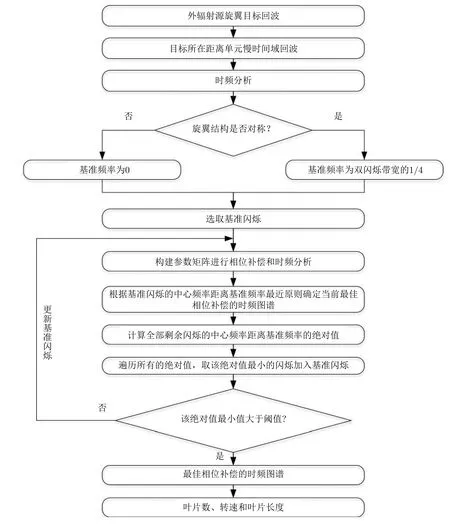
图4 算法执行框图Fig.4 The flowchart of the proposed method

(1) 采集目标原始数据，并进行距离向压缩获取目标所在距离单元的慢时间回波；

(2) 对原始数据进行时频分析，确定叶片结构对称与否；

(3) 根据叶片是否对称分别确定基准频率；

(4) 任意选取时频图谱中的一次闪烁作为基准闪烁；

(5) 根据设置的参数矩阵(µ,χ)构造补偿相位依次对慢时间回波进行相位补偿；

(6) 获取每次补偿回波的时频图谱，根据基准闪烁的中心频率距离基准频率最近的原则确定当前最优时频图谱；

(7) 遍历步骤(6)获得的最佳时频图谱中剩余所有闪烁，选取中心频率距离基准频率最近的闪烁加入基准闪烁，并回到步骤(5)；

(8) 直至时频图谱中所有闪烁的中心频率距离基准频率大于阈值，迭代循环结束，基准闪烁不再更新；

4 仿真实验

本节结合阿帕奇AH-64武装直升机旋翼[12]模型，利用GPS L1波段仿真信号进行实验，具体仿真参数如表1所示。为充分说明所提参数估计方法的有效性和对于不同参数空间设置的适应性，本文所提方法的仿真实验效果还与其他经典方法进行了比较。

4.1 基于相位补偿的参数提取方法实验结果

4.1.1 非对称旋翼目标实验

本部分仿真实验设置目标旋翼包含3个叶片，其他参数如表1所示。图5为旋翼目标的回波及时频分布，其中图5(a)为目标所在距离单元的慢时间域回波。可见，因为目标叶片的不断旋转，慢时间域回波主要由一系列相同间隔的谱峰构成，称之为闪烁。图5(b)为慢时间域回波序列的短时傅里叶变换，显然正频率闪烁和负频率闪烁交替出现在不同时间。另外，可以根据图5(b)估计得到单次闪烁的带宽为284.099 Hz。由前述分析可知，闪烁在时频域的不对称性主要由旋翼结构的不对称性引起，因此可以确定目标旋翼包含奇数叶片。

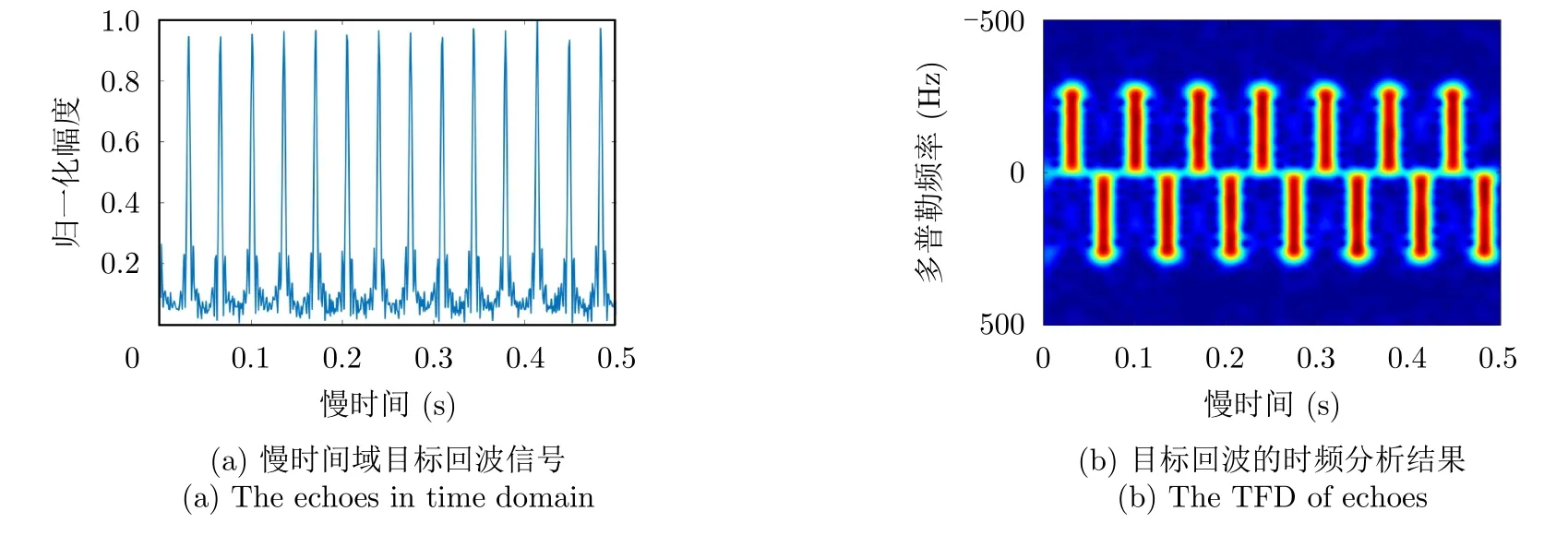
图5 非对称旋翼目标回波分析Fig.5 The echoes of asymmetry rotor targets

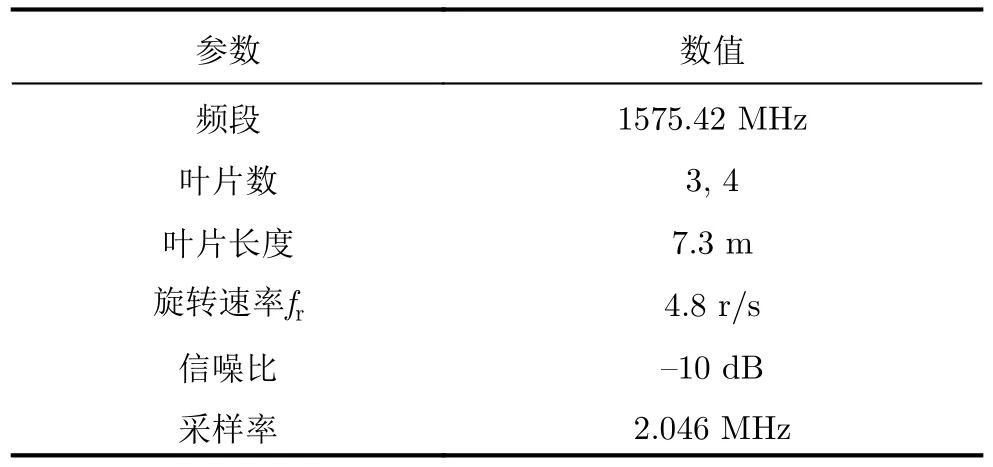
表1 仿真实验参数Tab.1 The parameters in simulation experiments

为确定目标旋翼包含的叶片数，采用相位补偿的方式对目标慢时间域回波进行处理，然后再进行时频分析，图6为相应的时频分析结果。本实验选择慢时间域上第2个闪烁(0.067 s)作为原始基准闪烁，然后根据基准闪烁的中心频率距离基准频率最近的原则选取最佳补偿的时频图谱，其中图6(a)为利用原始基准闪烁进行相位补偿获得的最佳聚焦效果。由图6可见，原始基准闪烁的中心频率接近零，而图6中的其他闪烁则在一定程度上偏离了零频，即仅仅原始基准闪烁被聚焦到零频。如前3.2.1节所述，此现象是由补偿相位的角频率不同于叶片旋转的角频率导致，相位补偿之后的多普勒频率在慢时间域呈现为不同幅度的振荡，与图3呈现的结果相吻合。为克服单个闪烁对聚焦效果稳定性的影响，本方法考虑利用多个闪烁进行联合聚焦。图6(b)所示为第2次迭代获得的最佳聚焦效果，此时基准闪烁包含有两个不同位置接近于零频的闪烁(0.067 s,0.171 s)。观察图6(b)发现，前3个闪烁都被聚焦于接近零频的位置，而其他闪烁则明显偏离零频。图6(c)和图6(d)分别表示第3、第4次迭代获得时频图谱，其基准闪烁分别包括3个闪烁(0.067 s,0.171 s,0.275 s)和4个闪烁(0.067 s,0.171 s,0.275 s,0.379 s)。迭代过程中基准闪烁的更新情况如表2所示。观察发现两图中各闪烁的分布结构大致相同，白色箭头所指的5个不同位置的闪烁均被聚焦于零频，因此该5个闪烁(0.067 s,0.171 s,0.275 s,0.379 s,0.483 s)可以确定为同一叶片在不同时间所产生。结合图6(c)和图6(d)可以发现，相同叶片两次不同时间的闪烁之间还间隔两次其他叶片的闪烁，这样就可以判断该旋翼目标包含有3个叶片。

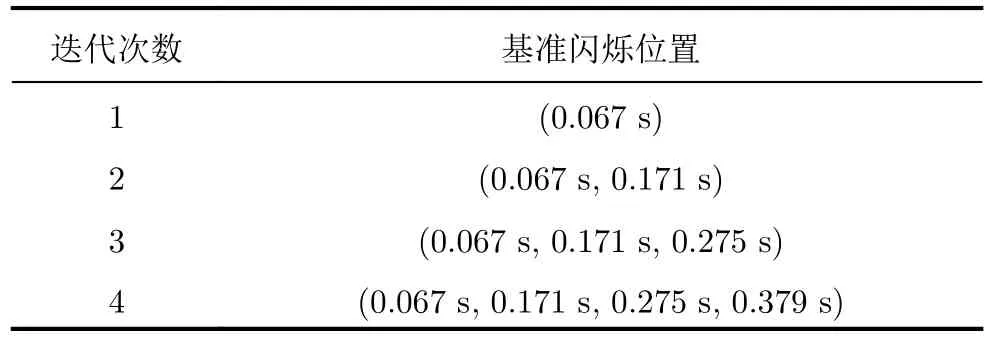
表2 非对称旋翼结构基准闪烁的更新Tab.2 The update of standard flashes in asymmetry rotor target

为更直观呈现相位补偿过程中前述5个闪烁中心频率的变化，图7给出了4次迭代过程中该5个闪烁中心频率的变化。其中圆圈状蓝色虚线表示第1次迭代之后该5个闪烁中心频率的变化，可见不同位置闪烁的中心频率变化较大，仅基准闪烁距离基准频率比较近；菱形紫色线表示第2次迭代之后该5个闪烁中心频率的变化，相比前一次，中心频率起伏变小，同样仅有基准闪烁距基准频率较近；依次矩形黑色虚线和三角形红色线分别表示第3、第4次迭代之后该5个闪烁中心频率的变化，两次迭代之间曲线变化不太明显，且基本等于零。可见，随着基准闪烁的逐渐更新，基准闪烁包含的闪烁数量也逐渐增加。图7表明随着基准闪烁数量的增加，相同叶片的闪烁越接近于基准闪烁。图8为最后一次迭代之后的参数搜索结果，其中Z轴表示基准闪烁的中心频率距离基准频率的平均值，X轴表示的是初始相位，Y轴表示叶片转速。图6(d)所示的最佳相位补偿效果对应的参数如图8中指数所示，可得到目标旋翼的转速为4.80 r/s。另外，根据式(22)得目标旋翼叶片长度为7.34 m。

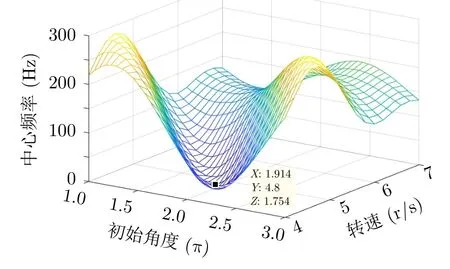
图8 最佳参数搜索结果Fig.8 The optimal parameters search result

4.1.2 对称旋翼目标实验

前述验证的是非对称结构旋翼目标的特征提取效果，由于对称结构旋翼产生的闪烁与非对称结构存在一定的差异，本部分用于验证所提方法对于对称结构旋翼目标的特征提取效果，实验目标为相同叶片长度、转速的旋翼，但包含4个叶片。

图9(a)所示为4个叶片旋翼目标原始回波的时频图谱，相比于图5(b)而言，此处时频图谱中的闪烁是对称结构，同一时刻的闪烁既包括正频率，又包括负频率，称为双闪烁，原因如3.2.2节所述。根据图9(a)可估计双闪烁所占带宽为571.73 Hz，此时fCD285.87 Hz。此处同样选择第2个双闪烁(0.067 s)作为原始基准闪烁，图9(b)为利用原始基准闪烁获得的最佳补偿之后的时频图，可估计其基准闪烁的中心频率为—141.28 Hz，约为双闪烁带宽的1/4，仔细观察时频图可见，该图中的双闪烁并不存在明显的规律性。图9(c)和图9(d)分别表示第2、第3次迭代之后的时频图，过程中所用的基准闪烁如表3所示。两次聚焦效果基本相同，表明此处只要结合两个双闪烁进行参数搜索，就可以实现比较精确的相位补偿。仔细观察时频图9(c)可以发现，经过相位补偿之后，首先可以确定第2次(0.067 s)、第6次(0.275 s)、第10次(0.483 s)双闪烁属于同一叶片对，如图9中白色箭头所示。其次考虑到同一叶片对所形成双闪烁的中心频率仅呈现两种对称的结果，第4次(0.171 s)、第8次(0.379 s)双闪烁的中心频率为第2次双闪烁的中心频率的负值，可见第4次、第8次双闪烁也与第2次双闪烁同属同一叶片对。因此，分析可知图9(d)中的第2次、第4次、第6次、第8次、第10次双闪烁属于同一叶片对，具体如图9中白色箭头所指示。此外，同一叶片对产生的双闪烁之间仅间隔一个双闪烁，且考虑到每个双闪烁对应两个叶片，那么可以获得该旋翼结构包含4个叶片。

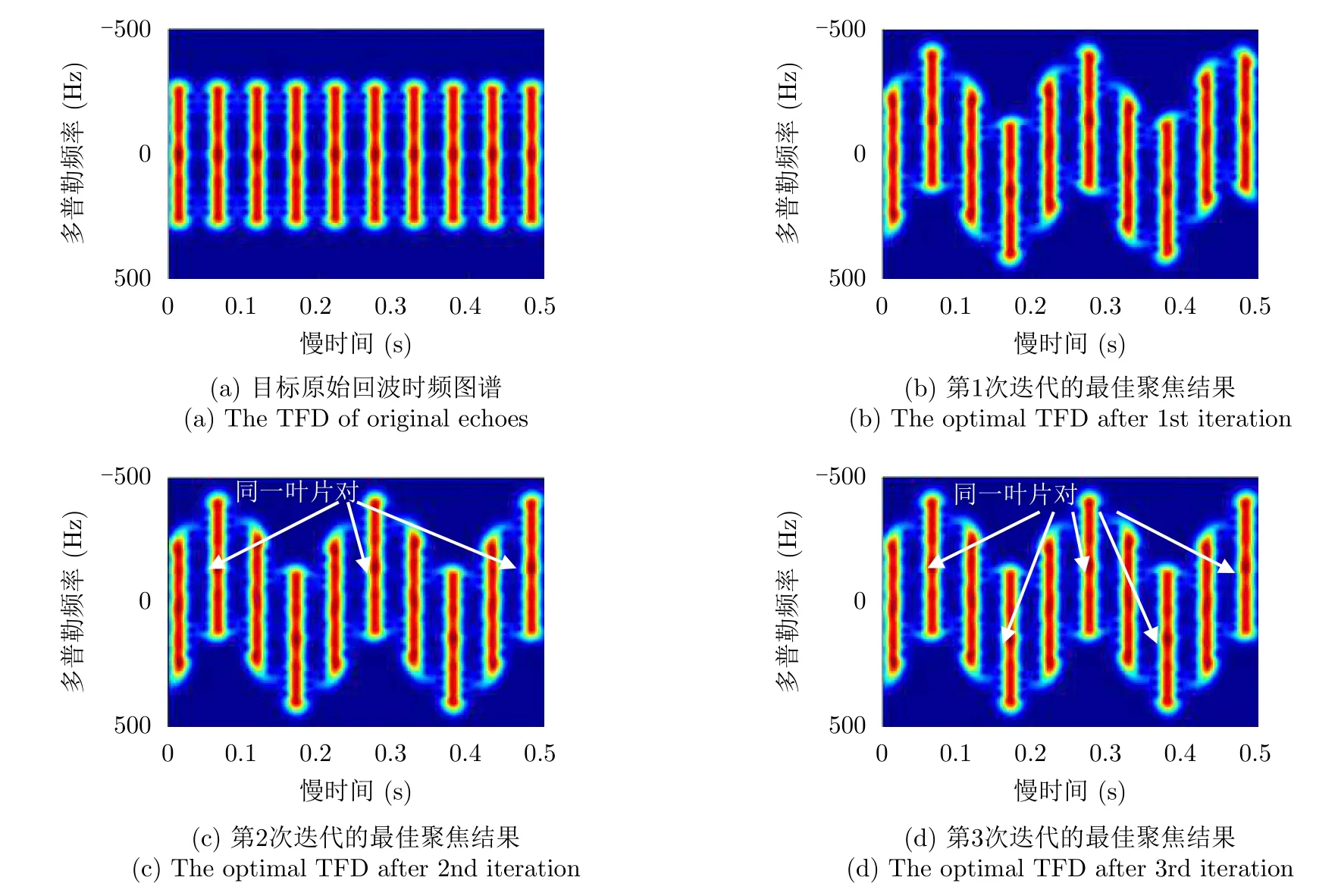
图9 对称旋翼结构相位补偿之后的时频图谱Fig.9 The TFD of symmetry rotor blade after phase compensation

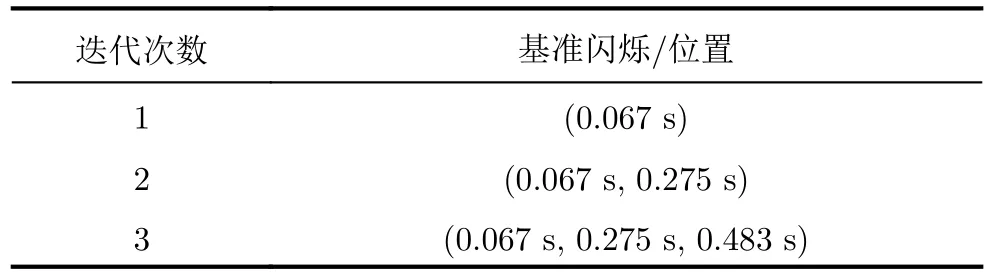
表3 对称旋翼结构基准闪烁的更新Tab.3 The update of standard flashes in symmetry rotor target

同样，图10给出了3次迭代过程中基准闪烁中心频率的变化，其中红色实线表示相位补偿的基准频率。图中圆圈状蓝色虚线表示第1次迭代之后中心频率分布情况，由于第1次选择的是0.067 s处的基准闪烁，所以仅仅使得该双闪烁的中心频率接近于基准频率，而其他双闪烁的中心频率则距基准频率较远。另外，图10中菱形紫色线表示第2次迭代之后中心频率的分布，其3个双闪烁的中心频率都相同程度地非常接近于基准频率。黑色矩形虚线表示第3次迭代之后中心频率的分布情况，其结果与第2次迭代几乎重合，可见在第2次迭代之后即可获得最佳相位补偿效果，即利用同一叶片两个不同位置的双闪烁作为迭代最优化准则基本可获得最佳的参数估计结果。

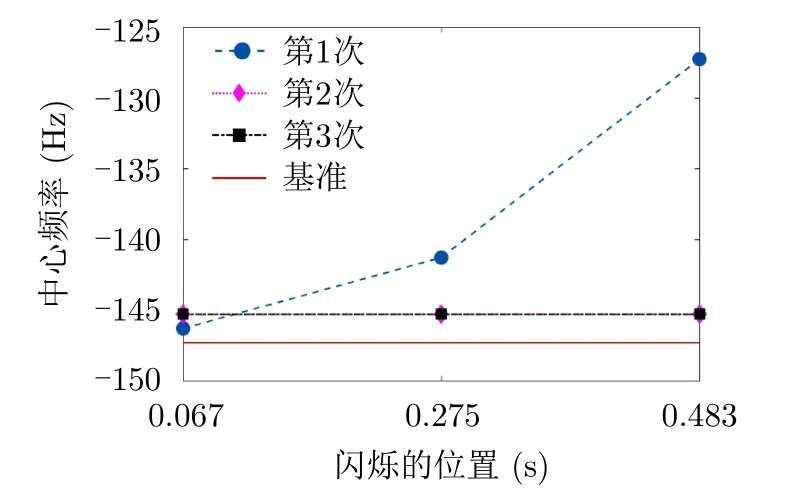
图10 迭代过程中基准闪烁中心频率变化Fig.10 The variety of center frequency of standard flashes during iterations

图11为经过最后一次迭代之后的参数搜索结果，由图11可见，基准闪烁中心频率距离基准频率最小值为2.00 Hz，几乎等于多普勒分辨率(2 Hz)，且达到最小值时叶片转速为4.80 r/s，相位为5.93 rad。因为不同叶片之间仅初始相位不同，所以此处关注的参数为叶片转速，与表1中参数设置相比，可见参数估计精度较高。然后综合目标所在的双基地参数，根据式(22)可计算获得叶片的长度为7.38 m，可见参数估计精度也比较高。

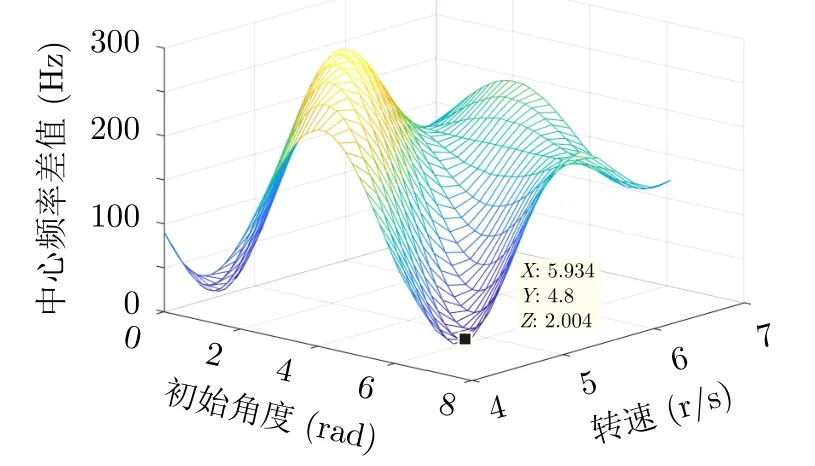
图11 最佳迭代之后的参数搜索结果Fig.11 The optimal parameters search result

4.1.3 参数估计精度分析

上述部分已经验证了本算法对于对称旋翼结构和非对称旋翼结构特征提取的有效性，下面进一步分析所提算法的参数估计精度。旋翼叶片数的估计误差直接决定算法的有效性，而且本算法利用时频图谱中基准闪烁之间的位置关系实现参数估计。另外，3.2.1节已经分析过补偿相位的初始相位差仅会带来闪烁的整体平移，而不会影响闪烁之间的相对位置关系。叶片长度的估计一方面受闪烁条带带宽估计的影响，另一方面也受旋转速度的影响，所以此处主要讨论旋翼转速的估计精度。图12给出了不同转速相位补偿之后获得的最佳时频图谱中基准闪烁的中心频率距离基准频率的差值，然后重复50次蒙特卡洛实验取平均值。图12中红色矩形实线转速为4.8 r/s的结果，其5个位置闪烁的频率差明显低于其他转速条件下的频率差，所以当补偿相位的转速与实际转速相等时可获得最佳聚焦效果。并且距离红色矩形实线最近的分别是转速为4.7 r/s和4.9 r/s的聚焦效果，其次是转速是4.6 r/s和5.0 r/s的聚焦效果。可见，当补偿相位的转速越接近目标实际转速时，其获得的补偿效果越好，因此利用本文所提出的相位补偿算法可以实现比较精确的旋翼目标特征提取。

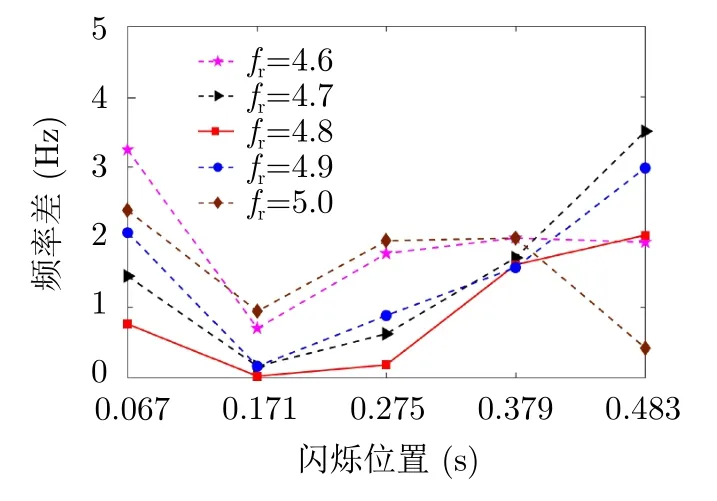
图12 不同角频率补偿相位对闪烁位置的影响Fig.12 The effect of different angular velocity on locations of standard flashes

4.1.4 叶片分离效果

本文所提算法通过相位补偿的方式将某个叶片的相位补偿完全，然后该叶片的闪烁就聚焦在零多普勒频率处。然后根据时频图谱直接获得旋翼包含的叶片数，并估计其他相关参数。此外，该算法还能实现旋翼叶片或叶片对的分离。以三叶片旋翼目标为例，图13为利用相位补偿之后的时频图谱进行叶片分析的效果。以相位补偿完全的叶片为基准，将其视为第1个叶片，如图13(a)中红色箭头所示；显然，根据各闪烁距离零频闪烁的时间维距离，依次可以确定第2个叶片(白色箭头所示)和第3个叶片(黄色虚线箭头所示)。对应到慢时间域回波，其时域闪烁可分离为相互不同的3个叶片形成，相同叶片形成的闪烁之前间隔两个其他叶片的闪烁，如图13(b)所示。

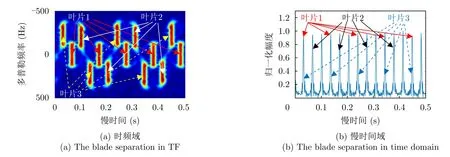
图13 叶片分离的效果Fig.13 The blade separation effect

为进一步说明所提方法对旋翼叶片分离的效果，图14和图15分别为对图5(a)和图6(d)进行叶片分离的结果，具体是利用峰值提取技术将各叶片形成的闪烁分别提取出来。前述部分已经估计得到旋翼包含3个叶片，所以分片分离后主要包含3个叶片，各叶片的起始相位自左至右分别为：1.75π,0.42π,1.09π，每个叶片的慢时域回波如图14所示。由图中可得各叶片谱峰之间的时间间隔约为0.105 s，为图5(a)中所示谱峰间隔(0.035 s)的3倍，与旋翼包含三叶片的结果相符。图15为各叶片回波的时频图谱，可见每个叶片时频图谱都呈现为正频率闪烁和负频率闪烁交替出现的情况。虽然形成闪烁均表示叶片与雷达系统之间形成镜面反射，但是该几何关系的形成可以分为两种情况：叶片靠近雷达运动和背离雷达运动。具体叶片运动方法与正负闪烁的对应关系与发射信号的相关，此处不作详细讨论。所以，本文所提方法不仅能实现旋翼参数的精确估计，而且可以实现不同叶片回波的分离，且能对应到不同的初始相位。

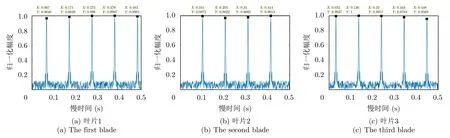
图14 叶片回波分离Fig.14 The echoes of different blade

4.2 其他经典算法效果对比

此处设置与4.1.1节相同的实验环境，设置旋翼包含3个叶片，利用经典的特征提取方法对信号进行处理。图16表示对慢时间域回波直接进行傅里叶变换处理的结果，可见回波频谱大致分布在—273.5～273.5 Hz带宽的范围内，与4.1.1节估计结果相近，但是该结果仅给出了多普勒频率范围，而没有呈现多普勒频率的变化趋势，因此难以提取出回波中的微多普勒频率信息。图17为Hough变换对原始时频图谱进行正弦曲线检测的结果，其中X轴表示转速，Y轴表示初始角度。可见转速估计结果依次为(4.9 r/s,4.7 r/s,4.7 r/s)，均值为4.77 r/s，进一步计算得到叶片长度为7.36 m。可见，受时频分析工具STFT分辨率的限制，Hough变换参数空间结果中的3个峰值都不够锐利，容易影响峰值检测的精度，进而导致参数估计结果精度比较低。

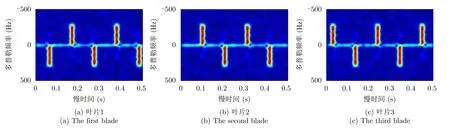
图15 时频图中的叶片分离Fig.15 The TFD of echoes of different blade

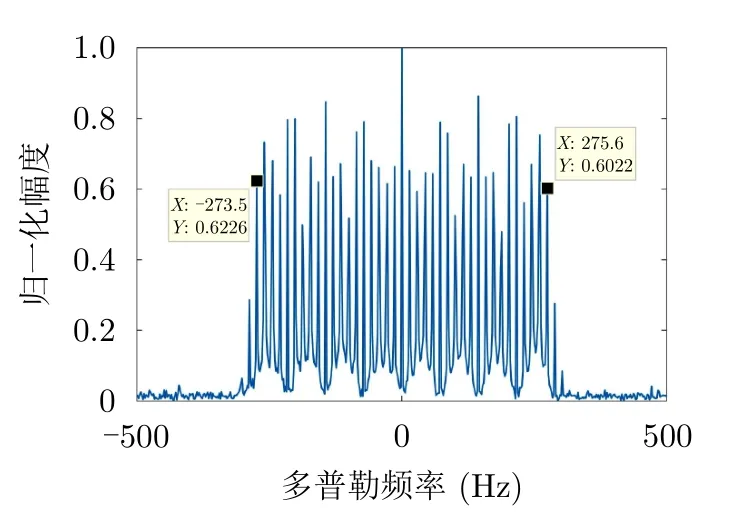
图16 傅里叶变换的结果Fig.16 The result of Fourier transform

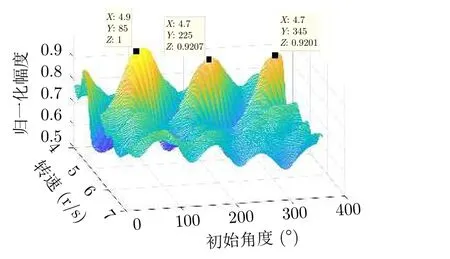
图17 Hough变换的结果Fig.17 The result of Hough method

图18为不同参数设置条件下的OMP算法实验结果，具体不同实验的参数设置如表4所示，图中X轴表示叶片长度，Y轴表示目标叶片的转速，Z轴则表示幅度。其中，图15(a)对应实验a的结果，可见图中包含3个峰值，可取该3个峰值指数的平均值作为实验a的参数估计结果。由于3个峰值分别位于不同的旋转速度上，即旋转速度估计结果不一致，所以对应的叶片数也就不相等，可认为该条件下的OMP算法不能获得目标的参数估计。虽然此时仍然可以通过3个峰值的均值计算出参数估计结果，但是均值计算结果没有意义，此处将无效的叶片长度与转速的估计结果写在表5内。图18(b)表示实验b的结果，由图中指数可知，3个峰值对应相同的转速4.80 r/s，对应叶片数为3。此时可以认为本条件下的OMP参数估计方法可以有效估计目标参数，进而可得目标旋翼的长度估计结果为7.45 m，具体实验b的有效参数估计结果如表5所示。图18(c)为实验c的结果，此处设置初相角在0～120°内分10等份。与图18(a)类似，此处3个峰值也对应不同的旋转速度，同样可以认为实验c参数设置条件下OMP算法无法获得有效的目标参数估计结果，实验c的相应无效结果也写在表5中。根据表5可知，当OMP算法无效时，其参数估计结果远远偏离真实值。因此，为保证OMP算法的有效性，该算法需要设定合适参数搜索区间和网格划分疏密。

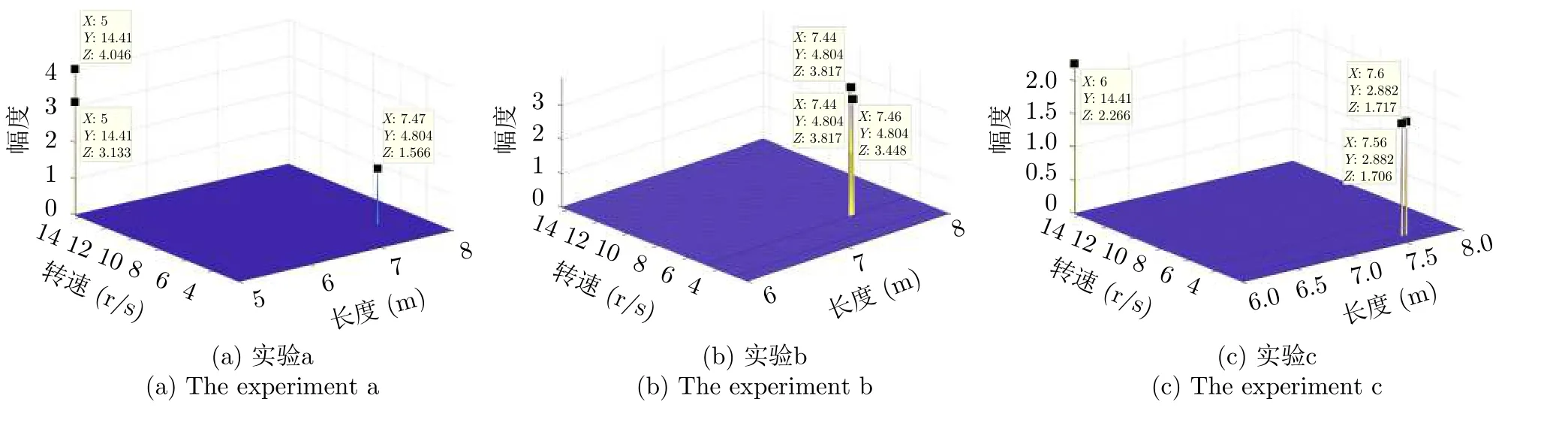
图18 OMP参数估计方法的实验结果Fig.18 The experiment result of OMP algorithm

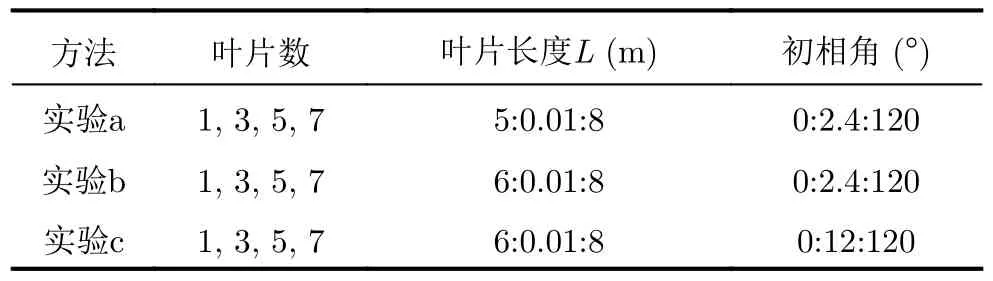
表4 OMP算法实验条件Tab.4 The experiment condition of OMP algorithm

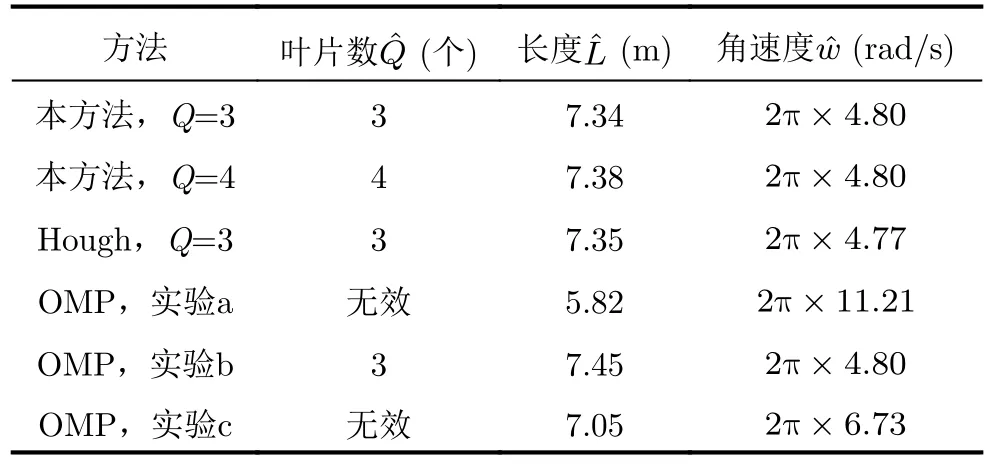
表5 参数估计结果对比Tab.5 The parameter estimation result of different algorithms

对比实验a与实验b的参数设置，发现基于OMP的参数搜索算法容易收敛到局域的极值，而不能稳定的收敛到全域的最值，导致参数估计结果可靠性较差。同样，比较实验b与实验c的参数设置，发现参数空间的网格化程度也会严重影响到OMP方法参数估计结果的有效性。

表5给出了不同实验条件下的参数估计结果。本文所提方法无论旋翼结构是否对称都能够实现有效的参数估计，且相比于Hough变换和OMP算法的参数估计精度更高。另外，基于OMP算法的参数估计仅能在实验b的参数设置条件下获得有效的估计结果，其他两个实验条件下无法获得有效的估计结果。综上所述，本文所提出的相位补偿算法相比Hough变换和OMP算法而言，可以实现性能更加稳定且结果更加准确的参数估计。另外，相比于其他经典算法而言，该算法还可以实现旋翼目标在回波域的叶片分离，为后续进一步的旋翼目标识别提供更多思路。

5 结论

本文分析了外辐射源旋翼目标微动信号模型，并结合时频域闪烁特征和微动信号特性，提出了一种基于相位补偿的旋翼目标参数估计方法。首先利用时频分析方法获得回波的时频图谱，然后根据闪烁的形成机理对回波信号进行相位补偿，并根据相位补偿结果估计得到目标的叶片数量、长度以及转速。在算法执行过程中，为获得更高的算法稳定性，通过迭代的方式逐渐增加闪烁的数量进行联合搜索，避免单个闪烁的不稳定性对算法性能的影响。另外，针对对称结构和非对称结构旋翼的不同特点，分别采用不同的基准频率，使得本方法对不同旋翼结构的适应性更强。最后利用仿真实验验证了本文所提方法具有更高的可靠性和更准确的参数估计结果，并且该方法可以有效实现旋翼目标在回波域的叶片分离，为后续进一步的旋翼目标识别提供更多的解决思路。