一种极化-多普勒气象雷达的射频干扰滤波方法

殷加鹏 李健兵 庞 晨 李永祯 王雪松

(国防科技大学电子信息系统复杂电磁环境效应国家重点实验室 长沙 410073)

1 引言

气象雷达可实现对大气高时间和空间分辨率的观测，是业界公认开展大气研究的主要技术手段之一[1]。由于可以同时获取气象目标微物理和动态特性，极化-多普勒气象雷达逐渐成为国内外开展大气研究的“标配”[2]。使用气象雷达进行大气观测与预报的先决条件是数据有足够的测量精度。然而，气象雷达常布置于人口密集区域，工作环境非常复杂，容易受到多种类型雷达环境干扰影响[3]。

特别地，电磁设备种类和数量日益增多、电磁用频活动越来越频繁，部分电磁设备工作频率与气象雷达频段存在重叠，气象雷达受射频干扰的影响案例屡见不鲜[4]。比较典型的案例包括美国的C波段终端多普勒气象雷达网和欧洲的C波段气象雷达服务网[5]。此外，气象雷达网中的雷达之间也会有同频信号的串扰，比如S波段美国国家气象雷达网[5]。

射频干扰在气象雷达显示器(Plan Position Indicator,PPI)上呈现点斑、条纹等样式，且出现的位置随机不可预知[6,7]。文献[8]研究了意大利北部S波段和X波段气象雷达射频干扰问题，对射频干扰的极化特性进行初步分析，指出对于当前业务化的同时极化测量体制雷达，射频干扰与气象目标极化特性大部分类似，难以直接区分。但该工作对射频干扰的特性研究不够深入，没有充分挖掘极化信息对于提取气象目标和射频干扰特性差异的潜力。

目前，气象雷达射频干扰滤波方法的研究以国外学者为主。对于简单射频干扰，可以采用时域方法进行滤除。通过比较每一个脉冲的幅度值与其邻域的中值，Lake等人[9]设计了一维中值射频干扰滤波器，但该滤波器的滤波效果有限。基于射频干扰在距离-时间域上幅值异样特性，Cho[6]提出了一种二维射频干扰滤波器，滤波效果有所提升。

然而，时域算法仅对于占空比较小的射频干扰可以达到较好的效果，当占空比较大时，由于没有足够的不受干扰影响数据，这类算法效果有限。在该条件下，文献[6]推荐使用多普勒滤波器，但并没有进行深入分析研究。事实上，射频干扰在频域上呈现的是“抬升的噪声”这一特性，而气象目标相对比较集中，若气象目标在频域上没有完全被射频干扰覆盖，则可以通过适当的滤波方法保留气象目标。文献[10]提出了一种基于模糊函数分类的极化-多普勒滤波器，但没有定量分析其性能。

为了解决气象雷达中射频干扰问题，特别是存在高占空比射频干扰情况下，本文采用极化-多普勒滤波器。基于同时测量得到的多普勒和极化信息，极化-多普勒技术，即谱极化技术可以综合表征气象目标的微物理和动态特性，可有效用于气象目标微物理特性反演[11]和非气象目标抑制[12]。

本文所使用的谱极化滤波器具体包括动态双谱去极化比(Moving Double spectral Linear Depolarization Ratio,MDsLDR)滤波器[12]和面向对象的谱极化(Object-orientated Spectral Polarimetric,OBSPol)滤波器[13]。这些滤波器可以用于同时滤除多种类型的杂波，它们最初被提出是用于滤除窄带杂波(包括动态的和地杂波)，在本文中将被拓展用于滤波射频干扰。具体地，该类型滤波器主要作用于距离-多普勒域，利用降雨目标和射频干扰的谱极化特性和距离-多普勒域上的连通特性差异，在尽可能多的保留降雨目标的情况下，滤除射频干扰。

典型的极化气象雷达根据是否在一个脉冲内完成极化散射矩阵的测量，可以分为同时发射同时接收(Simultaneously Transmitting and Simultaneously Receiving,STSR)体制和分时发射同时接收(Alternately Transmitting and Simultaneously Receiving,ATSR)体制[14]。而所使用的谱极化滤波器适用于不同类型的极化气象雷达。

本研究使用的雷达数据包括：(1)C波段脉冲多普勒STSR雷达；(2)X波段调频连续波ATSR雷达。首先，本文利用C波段雷达实测数据分析射频干扰时域、频域和极化域特性，然后建立射频干扰模型，再在X波段雷达数据仿真加入射频干扰，以验证滤波器性能。

论文的组织结构如下：第2节主要介绍极化气象雷达的分类和典型的极化参量。第3节对射频干扰的特性进行分析，主要包括时域、频域和极化域的特性。第4节建立射频干扰的模型，并利用实测数据进行仿真。第5节和第6节分别提出射频干扰滤波算法，以及定性和定量分析滤波效果。第7节对本文工作进行小结。

2 极化气象雷达与谱极化参量

2.1 极化气象雷达分类

极化气象雷达需要测量气象目标的极化散射矩阵，具体根据发射和接收电磁波的形式，可由2×2的复散射矩阵S表示为[15]

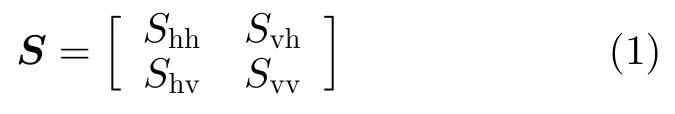
其中，Sxy是发射y极化，接收x极化的复散射参量，x极化和y极化都可以表示为水平极化h和垂直极化v。一般而言，极化雷达在探测诸如降雨等互易性介质的情况下，满足ShvSvh。

为了能测量目标的极化散射矩阵，目前主流的极化气象雷达按照发射和接收的形式不同可以分为ATSR体制和STSR体制，具体示意图如图1所示。如图1(a)所示，具有ATSR体制的雷达系统采用“交替发射两个正交极化、双极化接收”的模式，雷达系统的发射部分仅需要一路射频通路，发射信号通过极化捷变器交替传输至双极化天线的两个正交极化端口，雷达至少需要2个脉冲才能完成一次极化散射矩阵的测量。尽管雷达系统的脉冲重复频率有所下降，但由于分时极化测量体制雷达系统结构简单、易于实现，因此得到广泛应用。典型系统诸如荷兰代尔夫特理工大学的IDRA雷达[16]等。

如图1(b)所示，采用同时极化测量体制的雷达系统能够同时发射一组正交波形，然后雷达分别在两个正交极化通道上接收回波信号并进行处理。与分时极化测量体制雷达相比，同时极化测量体制雷达需要两条发射链路，其设计更为复杂。此外，由于STSR体制的气象雷达并没有使用极化捷变器，需要同时发射两个正交的极化波，该体制对雷达系统尤其是对天线交叉极化隔离度的要求远高于ATSR体制[17]。

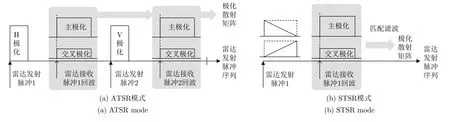
图1 极化气象雷达测量体制Fig.1 Measurement schemes of polarimetric weather radar

经理论和实践表明，STSR体制能够有效降低气象目标去相关效应对于天气预测的影响。此外，由于雨滴的极化散射矩阵近似为一对角阵，因此在STSR体制下，气象雷达并不对雨滴极化散射矩阵的交叉极化分量进行测量，而只对主极化分量进行测量。鉴于此，该体制用于气象雷达往往不采用正交波形，而是简单的单频脉冲信号。这种方案能够简化系统结构，降低雷达系统成本，同时保留雨滴极化散射矩阵的主要信息。目前主流的业务极化气象雷达，诸如WSR-88DP等都采用STSR测量体制。不仅如此，以Zrnić为代表的学者也认为，美国下一代极化相控阵气象雷达应该工作在STSR测量体制下[18]。

2.2 谱极化参量

本节讨论典型的极化气象雷达测量参量[13]。基于后向散射对照约束，雷达反射功率Zxy(r)可以定义为

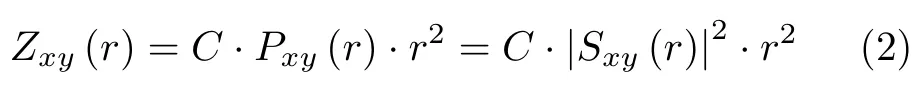
其中，Pxy(r)表示在距离r上发射y极化接收x极化的后向散射功率，C为雷达常数。特别地，Zhh(r)指代雷达反射率。

相应的极化参量，诸如差分反射率Zdr(r)，线性去极化比LDRhh(r)和LDRvv(r)，以及共极化相关系数ρco(r)可分别定义为

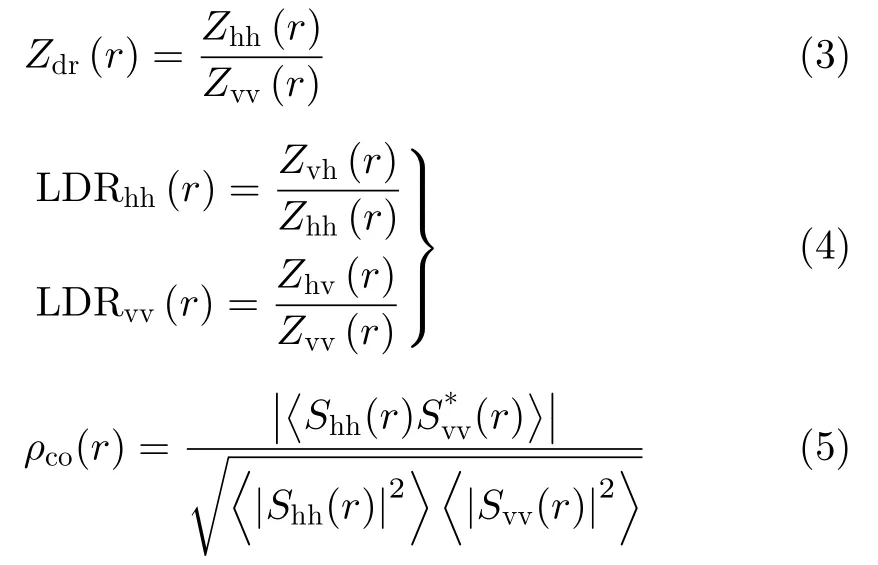
其中，ρco(r)中的〈〉表示集合平均，∗表示复共轭。

基于同时测量得到的多普勒和极化信息，谱极化技术可以综合表征气象目标的微物理和动态特性[12,13]。这有益于同时反演大气微物理信息和抑制非气象目标回波。与距离r和多普勒速度v相关的谱反射功率sZxy(r,v)定义为

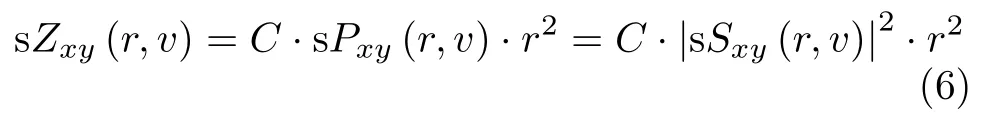
其中，sSxy(r,v) 表示二维的复距离-多普勒图，sPxy(r,v)表示谱功率。特别地，sZhh指代雷达谱反射率。相应地，本文可以定义谱差分反射率sZdr(r,v)、谱线性去极化比sLDRhh(r,v)和sLDRvv(r,v)以及谱共极化相关系数sρco(r,v)为

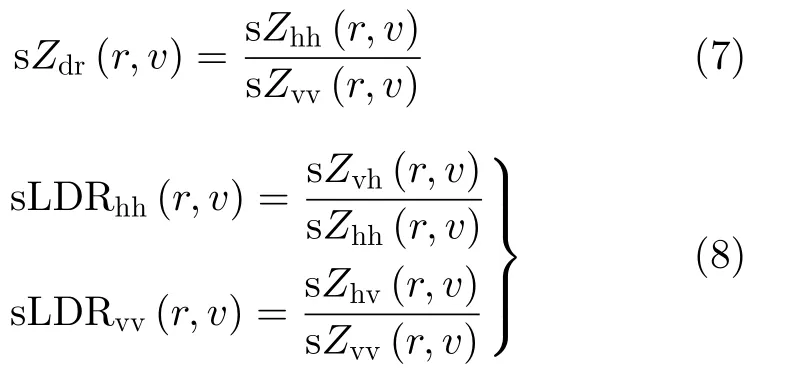
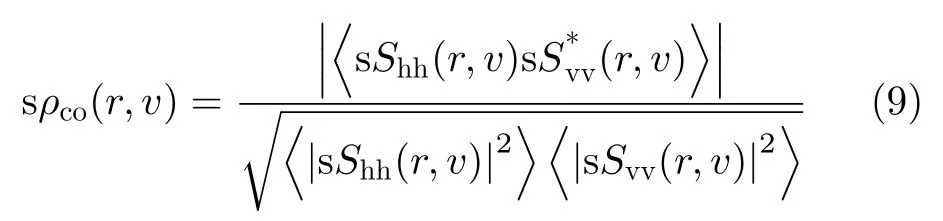
谱极化滤波作用于距离-多普勒谱图上，一般经过滤波后，只有表示降雨信号的区域会得以保留，杂波和噪声都会被滤除，因此可以更好地估计出测量参量。比如雷达反射率可以表示为

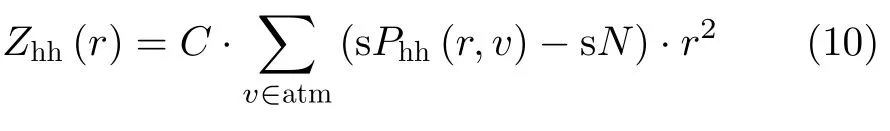
其中，v ∈atm表示谱图上属于降雨信号的点，而sN是整个谱图的谱噪声。通过对sPhh(r,v)绘制功率值直方图，直方图出现频次最大处所对应的功率值即可确定为谱噪声 sN。类似的针对每个距离-多普勒谱图确定噪声的方法可参照文献[19]。

此外，多普勒速度(r)和谱宽σv(r)可以分别表示为

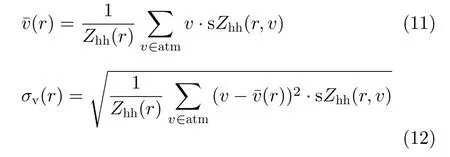
最后，共极化相关系数可以表示为

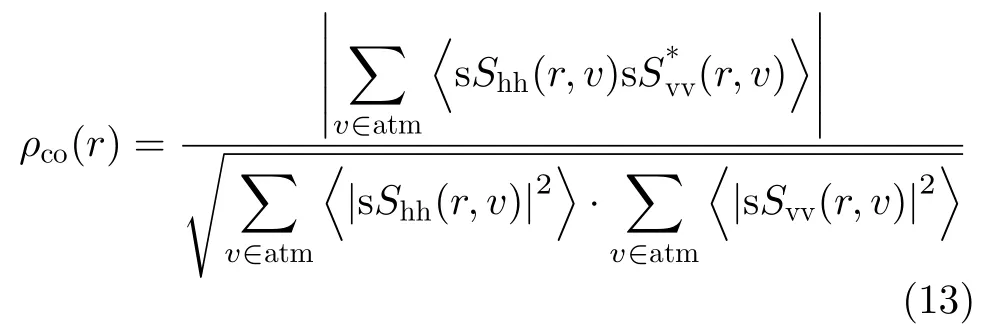
这几个参量后续也会用于定量评估滤波器性能。

3 射频干扰特性分析

对射频干扰特性的分析是设计有效射频干扰抑制算法的必要条件。本研究首先对实测的射频干扰特性进行分析，然后建立射频干扰模型，利用射频干扰模型进一步定量分析所设计滤波器的有效性。本研究实测的射频干扰数据源于荷兰皇家气象局的气象雷达系统，下面简称为KNMI雷达。荷兰共有2部气象雷达，均为STSR测量体制，具体的雷达参数如表1所示。这些雷达系统完成一次体扫需要的时间为5 min，共有16个扫描模式。

表1 KNMI雷达手册Tab.1 KNMI radar specifications

图2(a)所示的是典型气象雷达受射频干扰影响的雷达PPI图。该数据测量于2017年10月26日17:15(UTC时间)，从图2可以看出降雨在正北方向。而射频干扰是沿着某些方位角在整个距离方向上显示亮条纹的，会产生虚假降雨目标。其中，那些与降雨重合的射频干扰会影响实际雷达参量的估计。由于进入雷达接收机的射频干扰是异步干扰，这些干扰在某些方向角沿着距离维有相同的强度，然而从式(2)可知气象目标则与距离相关。

KNMI雷达标准滤波算法包括1个IIR滤波器、线性或者高斯递归插值法，然而该杂波抑制算法却无法滤除射频干扰。因此，有必要设计有效的射频干扰抑制算法，用于实时滤除射频干扰，满足雷达业务化的需求。

该雷达多普勒处理采用的数据大小为64，通过加窗可以抑制频谱泄露。该雷达PPI的第70帧数据被射频干扰影响，可以用于绘制典型的距离-时间图和距离-多普勒图，分别如图2(b)和图2(c)所示。从图2(b)可以看出，射频干扰以非常短的脉冲形式出现于距离-时间图上，其出现位置呈现不规则和不可预测性。由于射频干扰与雷达时序不同步，射频干扰出现于距离-时间图上主要取决于射频干扰的占空比和雷达天线的旋转速度。

通过对每一个距离单元的接收信号做傅里叶变换，可以得到典型的距离-多普勒图，如图2(c)所示。从信号理论可知，时域上的类似冲击信号对应于频域上是很宽的信号。从图2可以看出，降雨目标主要集中在距离100 km左右的负多普勒速度处，而射频干扰出现于某些距离单位，此时降雨目标与射频干扰有部分重叠。对比图2(b)和图2(c)可知，同一降雨目标在频域上呈现更小更集中区域且信号强度会更大，而射频干扰恰恰相反。因此，若采用频域滤波的方法，可以更精准地保留降雨目标。但是，对于射频干扰很强且与降雨目标大部分重叠的情况，即使采用频域滤波方法，也无法完整地保留降雨目标。

下面进一步分析射频干扰的谱极化特性。由于KNMI雷达工作于STSR模式，下面仅分析谱差分反射率sZdr和谱共极化相关系数sρco。图2(c)所对应的距离-多普勒图的sZdr和sρco如图3(a)和图3(b)所示。一方面，sZdr可以包含降雨粒子形状信息，曾用于风场反演中鸟和昆虫杂波的滤除[20]，然而从图3(a)可以明显看出，降水区域与射频干扰、噪声的区分并不十分明显。

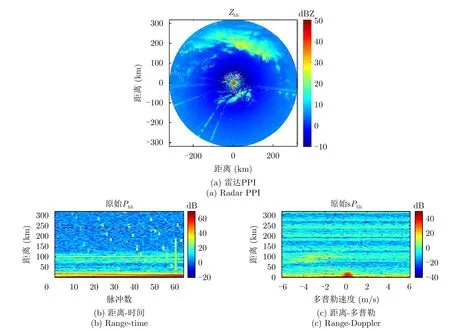
图2 KNMI雷达测量结果Fig.2 The measurements of KNMI radar

另一方面，sρco广泛用于区分降水粒子和非降水粒子[21]，然而从图3(b)可以看出，降水区域无法明显区分出来。这是由于sρco是相位信息，在STSR模式下，HH分量和VV分量是同一个脉冲测量得到的，所以射频干扰的sρco具有较大值。而在ATSR模式下，HH分量和VV分量是两个脉冲测量得到的，此时由于去相关效应，射频干扰的sρco值较小。而同样的降雨目标，在两种测量模式下，都可以保持较大的sρco值。因此，采用ATSR模式天然有助于滤除射频干扰。

事实上，对于STSR模式而言，其数据集为Hm和 Vm，其中m1,2,...,M,M为1个驻留时间内总的脉冲数，若采用数据分集的方法，通过选取H2n−1和V2n(或者H2n和V2n−1)其中n1,2,...,M/2，则可以模拟ATSR测量模式下的数据集。利用与图3(a)和图3(b)相同的数据，采用数据分集的方法绘制sPhh和sρco的距离-多普勒图如图3(c)和图3(d)所示。观测sPhh可以看出，降雨与射频干扰仍然部分重合，而仔细观察sρco则可以看出降雨信息仍保持较大的值，而射频干扰大大减小了。若在分集后的数据上采用谱极化滤波则能实现保留降雨目标的同时滤除射频干扰，这为STSR雷达抑制射频干扰提供了一种技术途径。

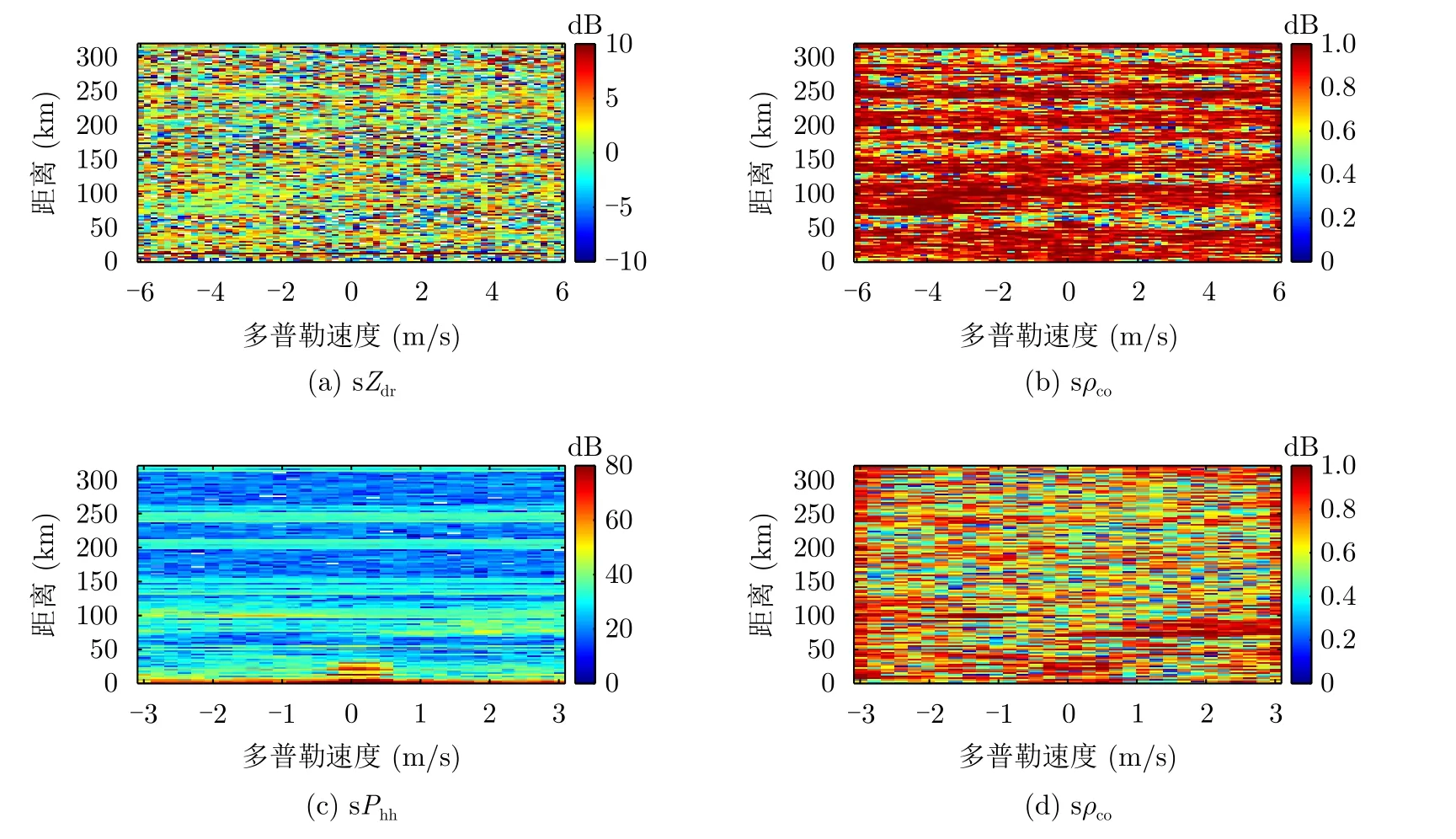
图3 KNMI雷达的谱极化参量Fig.3 The spectral polarimetric variables of KNMI radar

事实上，总结射频干扰极化参量与不同极化态的电磁辐射源的关系如表2所示。随着电磁辐射源从H极化变成V极化，射频干扰的Zdr的dB值从正到负，而降雨的Zdr值主要分布在0 dB附近，因此仅仅使用Zdr阈值来区分降雨和射频干扰是不够的。对于射频干扰的ρco而言，在辐射源为非严格H或者V极化情况下，STSR测量模式下得到的值都较大，而在ATSR测量模式下得到的值都较小；降雨的ρco值在两种测量模式下都保持较大。因此，ATSR测量模式天然有助于抑制射频干扰，而STSR测量模式可以通过数据分集的方法，得到ATSR子集，然后用同样的方法滤除射频干扰。

表2 射频干扰极化参量与不同极化的辐射源的关系Tab.2 The relationship between polarization variables and RF source with different polarization

4 射频干扰模型建立

通过对图2(b)中的距离-时间图的研究，建立射频干扰模型如图4所示。图中X轴表示慢时间，Y轴表示快时间。蓝色脉冲表示雷达发射脉冲，红色脉冲表示射频干扰信号，射频干扰进入雷达接收机的时刻是随机的。射频干扰模型可以用2个参数来描述，即射频干扰脉冲长度LRFI和射频干扰重复时间TRFI。具体地，射频干扰脉冲长度LRFI定义为

其中，l是整数，ΔR是雷达距离分辨率。此外，我们定义ΔtΔR/2c,c是光速。射频干扰重复时间TRFI可以定义为

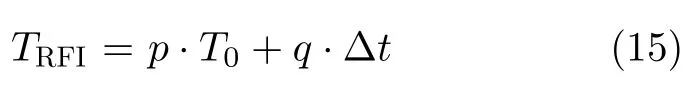
其中，p和q都是整数，T0是脉冲重复时间。不同的LRFI和TRFI组合可以得到不同的射频干扰模式，或稀疏或稠密。然而，对于频域滤波而言，射频干扰在时域-距离图上的稀疏度并不影响其滤波结果。

本文将图4的射频干扰模型用于IDRA雷达数据，以验证模型的有效性。IDRA雷达是荷兰代尔夫特理工大学研制的X波段高分辨极化-多普勒气象雷达。该雷达的测量模式为ATSR，其具体的参数如表3所示。自2009年4月至今，雷达数据均可以在网上免费下载。

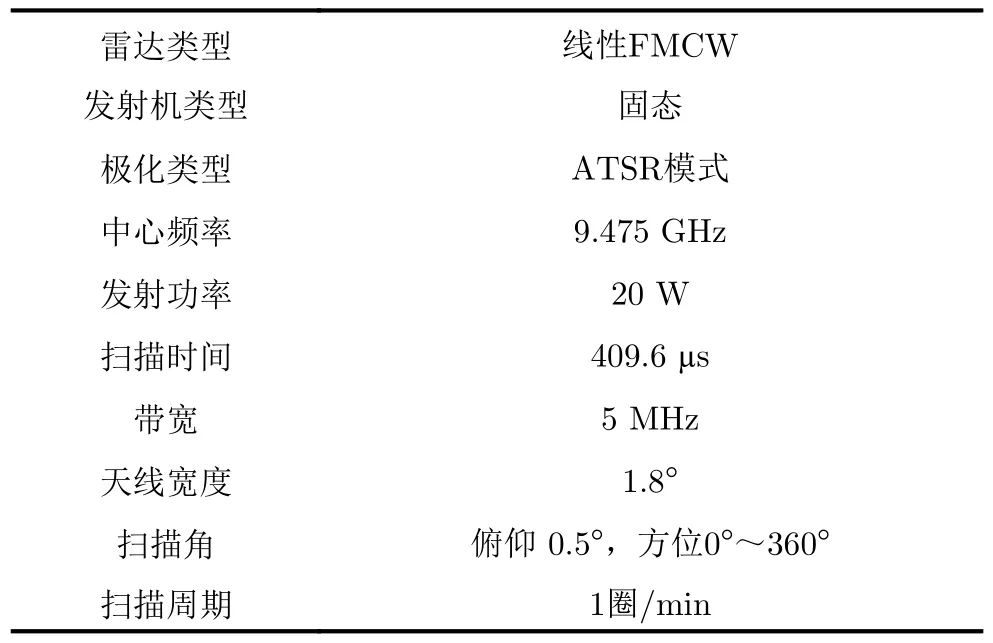
表3 IDRA雷达参数Tab.3 IDRA radar specifications

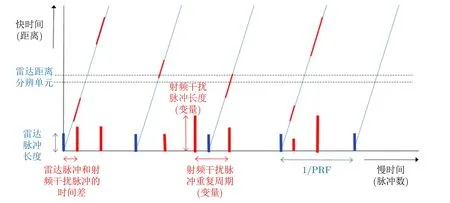
图4 射频干扰时域模型Fig.4 The signal model of radio frequency interference in time domain

本文使用测量于2017年4月26日00:00(UTC时间)的数据，其原始雷达PPI如图5(a)所示。本文在第84,90,100,120等几个谱图中分别加入INR为25 dB的射频干扰，得到如图5(b)所示的雷达PPI。加入仿真射频干扰前后的距离-时间图如图5(c)和图5(d)所示。对比这两个图可以看出，射频干扰呈现不规则的形状，部分还与降雨信号重合，这与实测的射频干扰数据相吻合。进一步分析对应的距离-多普勒图，如图5(e)和图5(f)所示。从图中可以看出，加入射频干扰后，谱图的整体背景噪声有所“抬升”，且部分处于降雨区域边缘的降雨信号被背景噪声遮盖住。进一步，选取距离2.4 km处的原始功率谱和加入射频干扰后的功率谱，如图5(g)所示。从图5可以看出，加入射频干扰后，噪声电平被抬高了超过10 dB，而此时降雨和地杂波保持不变。如果通过适当的频域滤波方法，可以仅保留降雨目标，那么就可以完全消除射频干扰的影响。

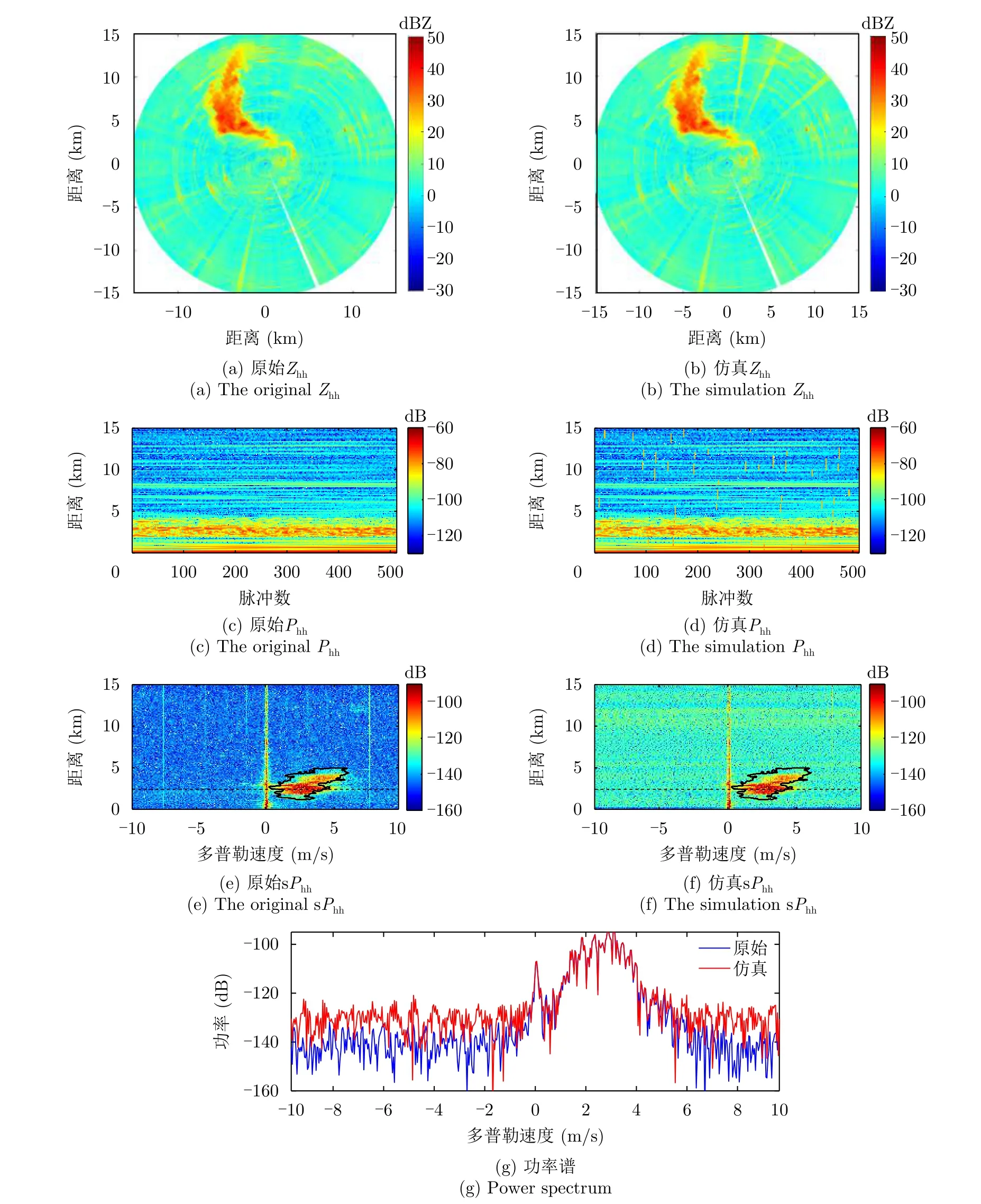
图5 IDRA雷达测量结果Fig.5 The measurements of IDRA radar

进一步绘制原始谱极化分量和加入射频干扰(INR分别为15 dB和25 dB)后的谱极化分量，如图6所示。可以看出，原始的sLDR 和 sρco中，降雨信号可以比较清晰地区分杂波和噪声。而加入射频干扰后，部分处于降雨区域边缘的降雨信号被背景噪声遮盖住。

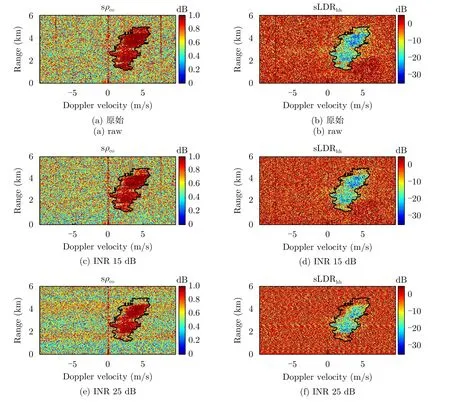
图6 不同INR条件下的IDRA雷达的谱极化分量Fig.6 The spectral polarimetric variables of IDRA measurements in different INR conditions

5 射频干扰滤波算法设计

本节主要针对射频干扰抑制问题，利用降雨目标和射频干扰的谱极化特性和距离-多普勒域上的连通特性差异，设计谱极化滤波器，在尽可能多的保留降雨目标的情况下，滤除射频干扰。谱极化滤波器作用于距离-多普勒域，通过产生一个{0,1}的二元滤波值，其中“1”表示降雨信号，作用于原始的功率谱图，实现保留降雨目标和滤除干扰。

最近，作者提出了两种谱极化滤波器，即MDsLDR滤波器[12]和OBSPol滤波器[13]，用于滤除窄带动态杂波和噪声。由于射频干扰在距离-多普勒域上呈现的是“抬高的噪声”这一特性，故而所设计的谱极化滤波器仍然可以适用。文献已证明这两款滤波器在滤除窄带动态杂波和噪声都有很好的性能，且OBSPol滤波器可以保留更多的弱降雨目标。但是，当降雨与杂波在频域上重叠时，所设计的滤波器无法实现仅保留“纯降雨目标”。MDsLDR滤波器和OBSPol滤波器的流程图如图7所示，下面简单描述各自的具体工作原理。

MDsLDR滤波器主要分为4个步骤，如图7(a)所示。第1步是利用双线性谱去极化比滤波器，第2步是沿着多普勒维使用一个滑动窗用于滤除窄带杂波，第3步是利用二维的滑动窗来恢复去除的降雨和消除剩余杂波。最后，用数学形态学方法进一步恢复降雨信号。MDsLDR滤波器需要雷达系统具备交叉极化测量能力，即雷达工作于ATSR测量模式，而大部分业务气象雷达为STSR模式，不具备该条件。

OBSPol 滤波器提出的初衷就是为了解决大部分STSR业务气象雷达的杂波滤除问题。OBSPol滤波器也分为4个步骤，如图7(b)所示。第1步是利用谱极化参量进行预滤波处理，可以选用常见的sρco。第2步用数学形态学方法恢复降雨信号。第3步把距离-多普勒图中连通的区域按照面积大小排序，归纳为不同的对象。第4步针对每一个对象，用额外的参量进行滤波处理，然后把这些参量合成一个最终的滤波结果。其中，若第1步采用sLDR，则可以是ATSR模式下的OBSPol滤波器。

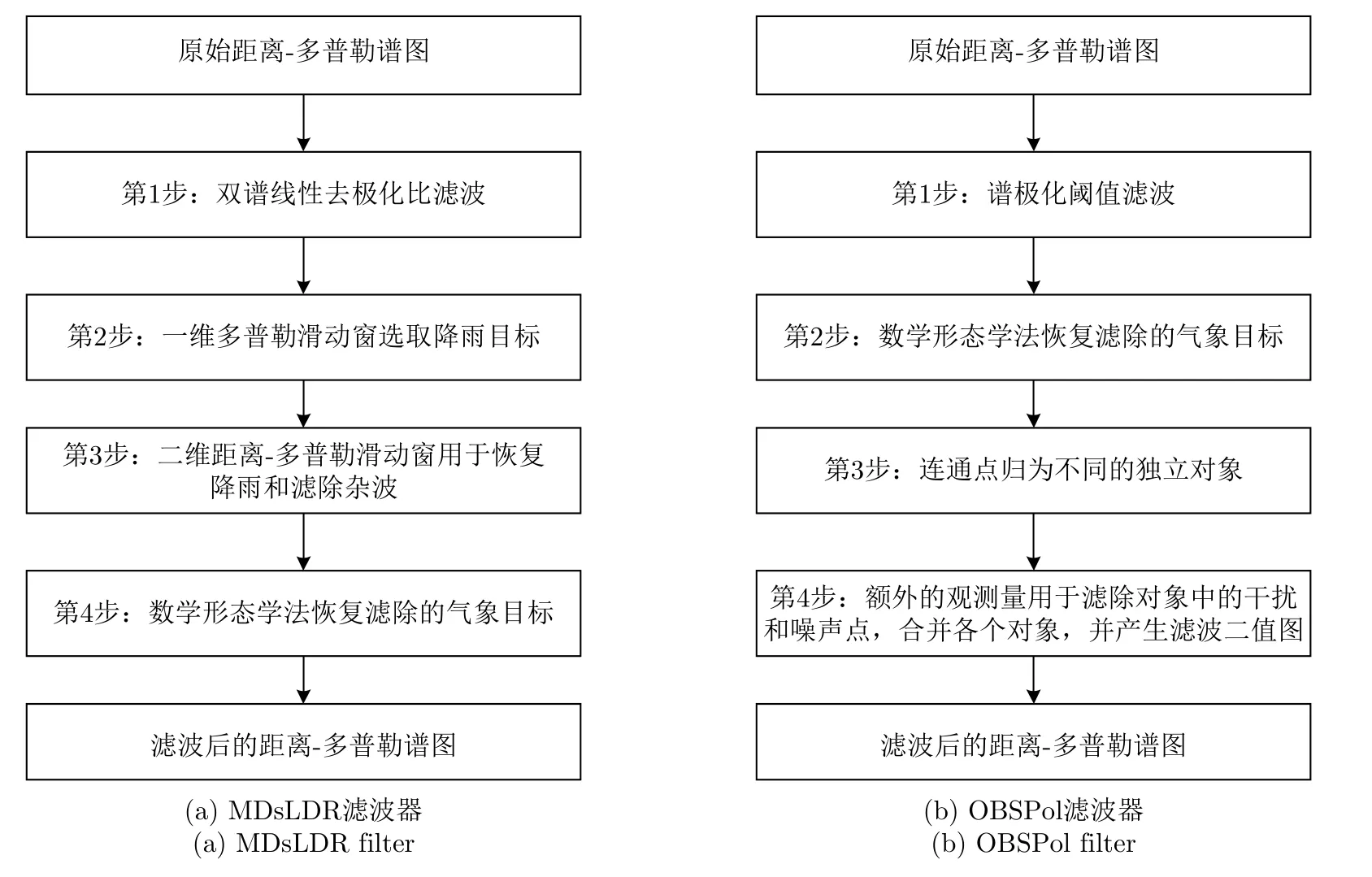
图7 谱极化滤波器流程图Fig.7 The flowchart of spectral polarimetric filters

为了更好地分析对比谱极化滤波器的效果，先简要介绍下IDRA雷达的标准处理方法(Standard Processing,SP)。SP处理由零多普勒滤波器、双线性谱去极化比滤波器和噪声门限法组成。上述处理完后，计算每个距离单元剩余的“1”的总数，看是否大于总多普勒处理脉冲数的2%，若不是，则将整个距离单元置“0”。

最后，为了定量衡量滤除射频干扰的有效性，根据混淆矩阵理论，本文定义距离-多普勒域上的检测概率Pd为

其中，TP表示降雨被判断为降雨的点数，FN表示降雨被判断为杂波的点数。虚警概率Pfa定义为

其中，FP表示杂波被判断为降雨的点数，TN表示杂波被判断为杂波的点数。此外，还可以通过定义均方误差(RMSE)用于衡量滤波性能。对于给定的距离-多普勒谱图，若有R个距离单元包含降雨，那么对于任一参量X的RMSE可以表征为其中，Xtru(r)是距离为r处的测量参量的真值，Xest(r)是测量参量的估计值。参量X可以是雷达反射率、差分反射率和共极化系数等。

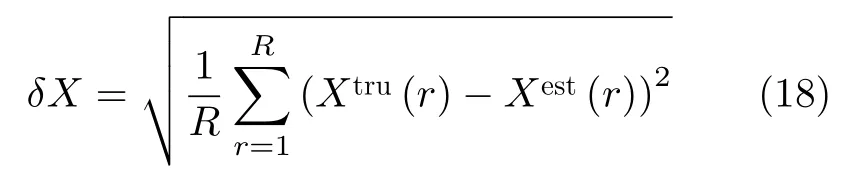
6 射频干扰滤波结果分析

6.1 ATSR雷达

为了评估ATSR雷达中谱极化滤波器对射频干扰滤波性能，本文用IDRA雷达数据。首先，采用图5的第84个谱图的数据，加入INR为25 dB的射频干扰信号。利用不同处理得到的结果，如图8所示。从图8可以看出，经过不同的处理后，降雨信号都有所损失，这主要是因为射频干扰信号较强，部分较弱降雨信号受到较大影响。SP处理后，有部分射频干扰得以保留下来，而其他几个谱极化滤波器可以完整地去除射频干扰。从降雨信号保留完整度来看，OBSPol滤波器使用sLDR效果最佳。

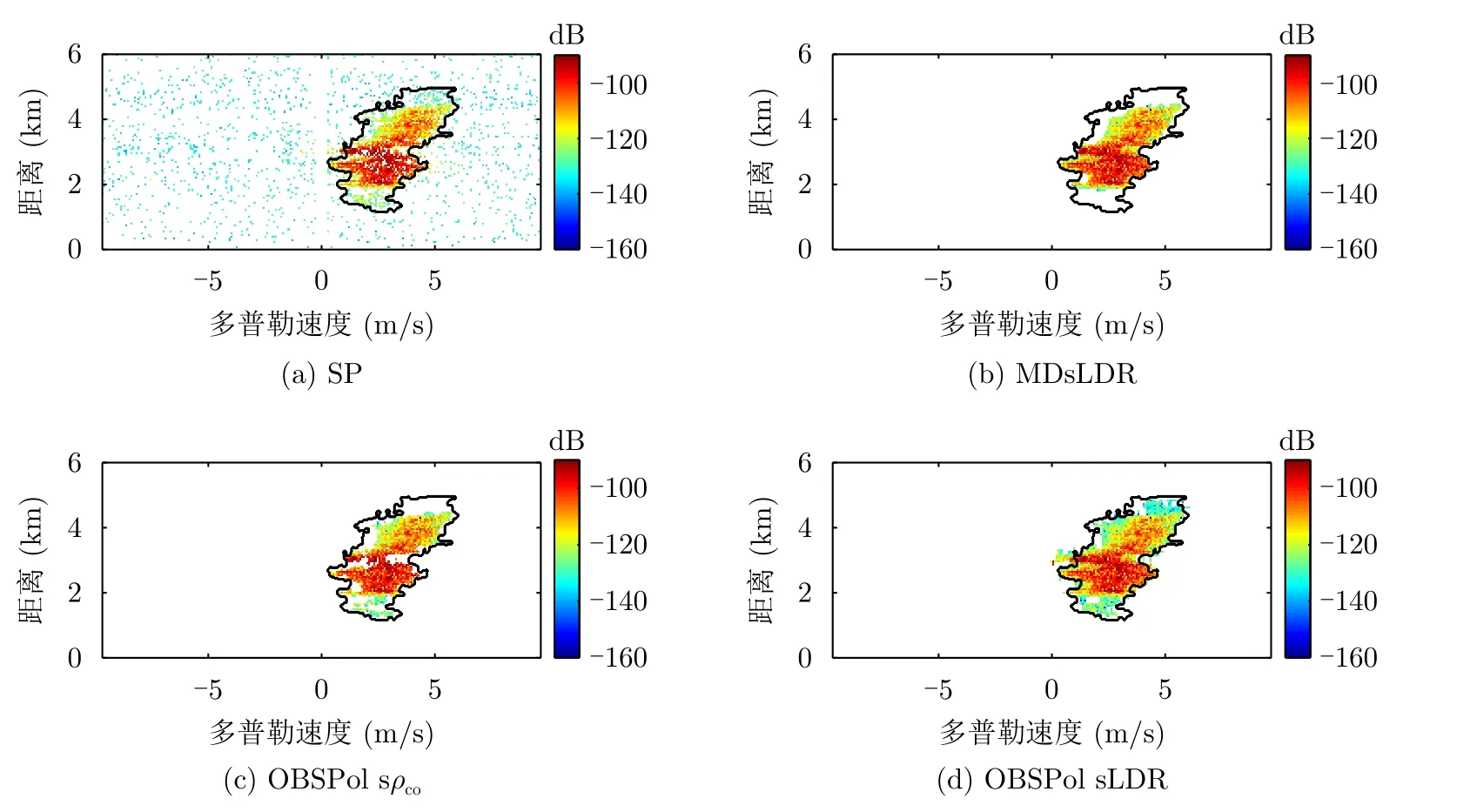
图8 不同处理后的距离-多普勒谱图Fig.8 The range-Doppler spectrogram after different processing

下面定量分析不同的处理对射频干扰滤除的效果。绘制不同INR条件下，检测概率Pd、虚警概率Pfa、反射率和共极化系数的RMSE的曲线图，如图9所示。其中，INR的范围为[–5 dB,25 dB ]，从图9可以看出，随着INR的增大，Pd值减小，这主要是因为更多强度更弱的降雨信号被“抬高的噪声”遮盖了(降雨的sLDR值增大，sρco值减小)。Pfa值都比较小，特别的谱极化滤波后，基本上可忽略不计。反射率的RMSE随着INR的增大，逐渐增加，这是由于INR增大了，更多的射频干扰得以保留。本案例中，MDsLDR和SP处理，相比于另外两种处理方式，效果更差。但原因却不相同，MDsLDR处理是只保留了强降雨信号，而观测Pfa可以看出，SP处理是保留了更多的射频干扰。最后，如图9(d)所示，共极化系数的RMSE与反射率的RMSE类似，但此时MDsLDR处理后性能最佳，这是因为MDsLDR滤波器可以完全滤除射频干扰和噪声。

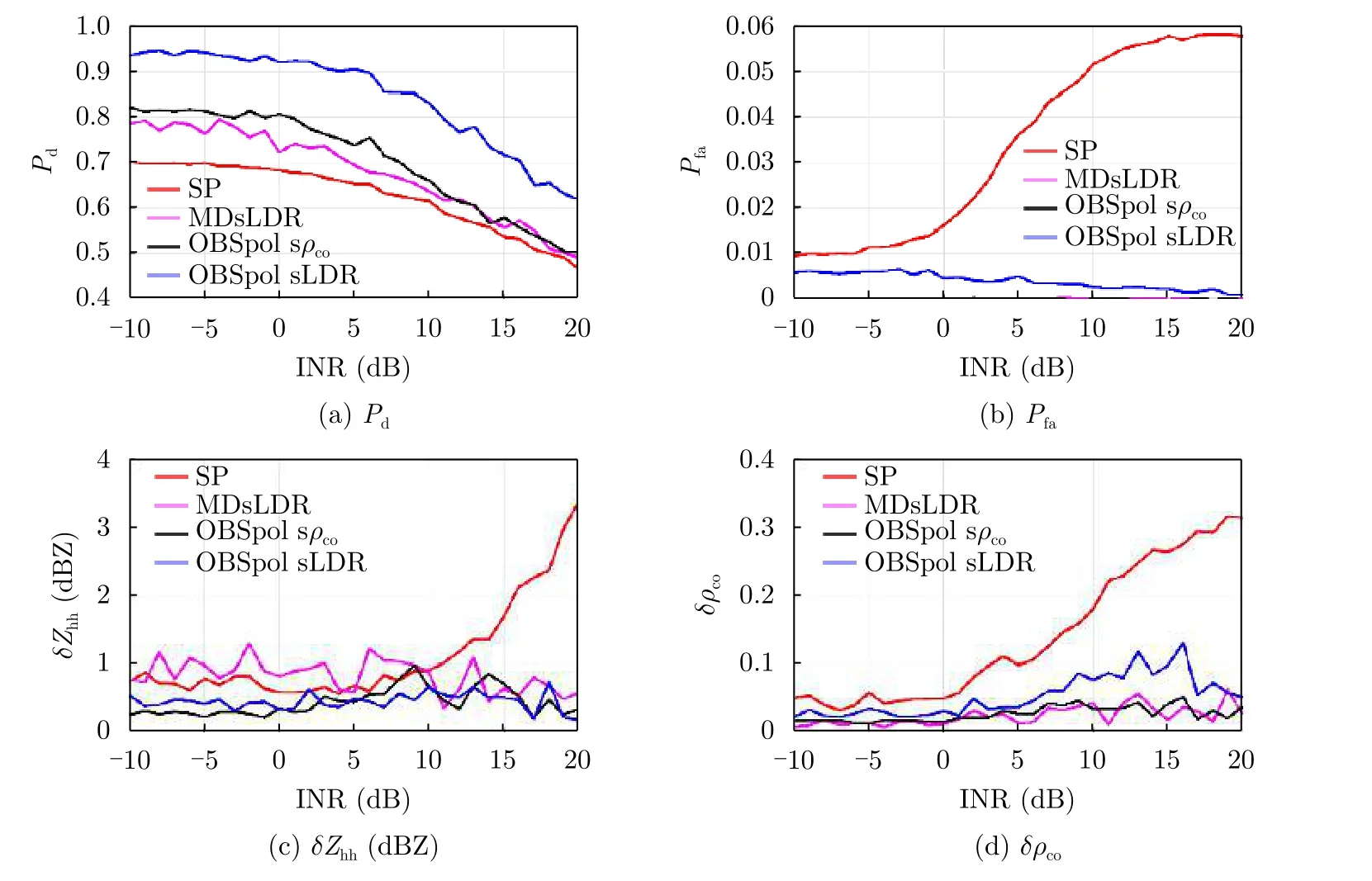
图9 不同处理后的性能指标与INR的关系Fig.9 The relationships between the metrics after different processing and the INR

最后，对雷达PPI的滤波结果也需要进一步检验，以证明滤波效果。在原始的雷达PPI上加入射频干扰如图5(b)所示，而本文的处理是基于该图，相应的结果如图10所示。SP处理保留了大量的杂波和噪声，相比之下，谱极化滤波器可以更好地对射频干扰和窄带动态杂波进行滤除。具体地，OBSPol 滤波器可以更好地保留弱降雨信息，使得降雨区域看起来更加连续。

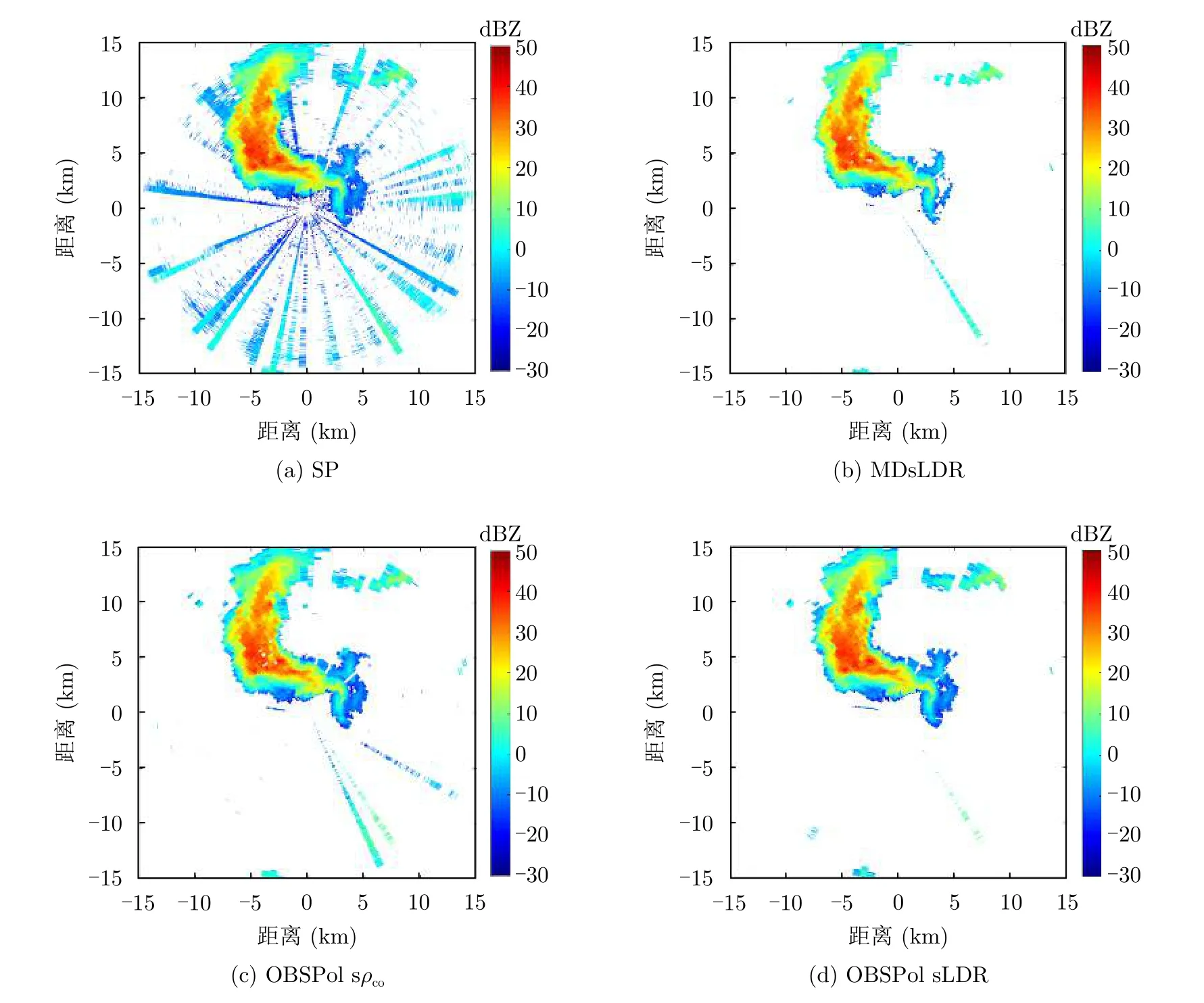
图10 不同处理后的IDRA雷达PPI图Fig.10 The IDRA radar PPIs after different processing

6.2 STSR雷达

6.1节利用ATSR雷达数据仿真加入射频干扰，验证了谱极化滤波器在射频干扰滤除的有效性。对于STSR雷达而言，其没有交叉极化测量能力，本文只能使用sρco参量和OBSPol滤波器。但此时由于射频干扰同时进入两个接收通道，射频干扰呈现较强的相关性，即sρco数值较大。但可利用数据分集的方式，模拟ATSR雷达数据集。具体地，OBSPol滤波器中sρco可以分为数据分集前后的sρco。本小节使用的数据即为图2所示，多普勒处理采用的数据大小为64，原始反射率和差分反射率以及数据分集前后的滤波结果如图11所示。

仿真中以20帧为步进在第60帧到第220帧的谱图中分别加入极化态为以5°为步进的5°～45°的线极化的射频干扰，结果如图11(a)和图11(b)所示。从图11可以看出，部分仿真射频干扰与真实射频干扰较为接近。使用不分集和分集的OBSPol滤波器的滤波结果，分别标记为STSR和ATSR，结果如图11(c)—图11(f)所示。使用不分集的OBSPol滤波器只能滤除INR小于10 dB的射频干扰，无法完全滤除射频干扰。而采用数据分集的OBSPol滤波器可以有效滤除所有的射频干扰。谱极化滤波器可以增强雷达对降雨目标的观测能力，以及雷达的数据质量。

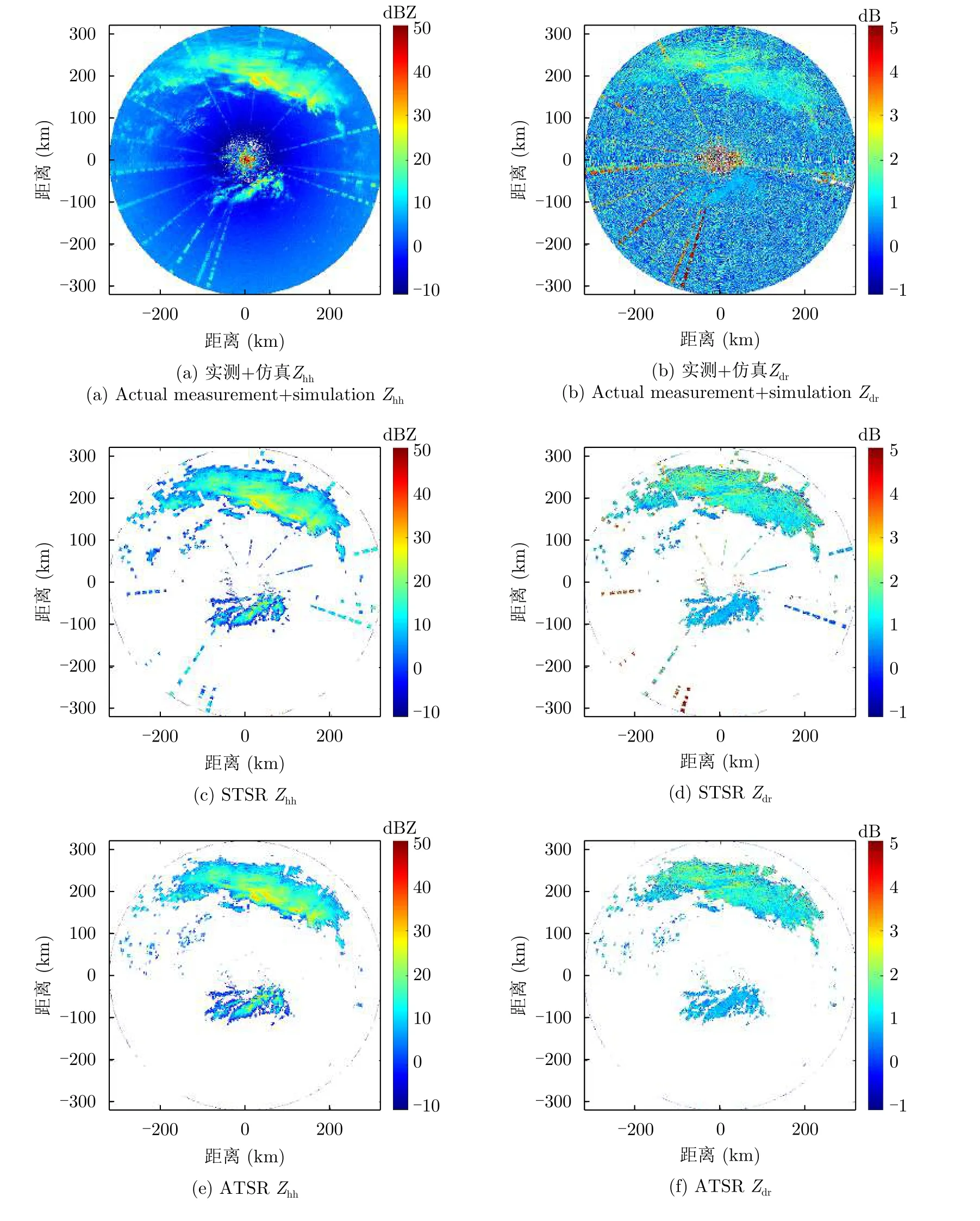
图11 不同处理后的KNMI雷达PPI图Fig.11 The KNMI radar PPIs after different processing

7 结束语

当前，极化-多普勒气象雷达是业界公认开展大气研究的主要技术手段之一。针对与日俱增的射频干扰对气象雷达的影响问题，本文提出利用谱极化滤波器来滤除射频干扰。首先利用C波段气象雷达的实测数据研究射频干扰的时域、频域和极化域特性，建立射频干扰信号模型。射频干扰的频域特性表现为“抬升的噪声”，而两个通道相关性则与极化雷达类型有关。对于STSR雷达而言，通道相关性较强；而对于ATSR雷达，通道相关性较小。然后，用上述获得射频干扰特性，在X波段ATSR雷达的数据中仿真加入射频干扰信号，通过定性和定量分析，验证谱极化滤波器的有效性。具体使用的谱极化滤波器为MDsLDR和OBSPol。总体看来，在ATSR雷达中利用谱极化滤波器可以有效保留降雨目标且滤除射频干扰。最后，针对STSR雷达，本文提出利用数据分集的方法，STSR雷达的实测数据可以模拟ATSR雷达数据，再利用谱极化滤波器实现射频干扰滤除，同样可以取得较好的滤波效果。