联合脉压与Radon傅里叶变换的长时间相参积累方法

裴家正 黄 勇* 陈宝欣 关 键* 蔡 咪 陈小龙

①(海军航空大学 烟台 264000)

②(92337部队 大连 116000)

③(91321部队 金华 321000)

1 引言

传统相干雷达系统采用先脉冲压缩后相参积累(杂波抑制)的顺序级联信号处理方案[1]。根据多普勒效应，目标或平台的运动会导致回波信号的频率与发射频率不同，发射的多个脉冲相当于在时域对多普勒信号进行采样。时域的相参积累常被用于检测强杂波中的目标，也可用于提高雷达的横向分辨率。最常用的两类处理方法是运动目标指示(Moving Target Indicator,MTI)和脉冲多普勒处理。前者的本质是通过高通滤波器滤掉低频杂波，并不改善目标的响应；后者是对每一距离单元的数据做谱分析，如离散傅里叶变换(Discrete Fourier Transform,DFT)等，可以得到较为准确的目标运动参数[2,3]。

常用的相参积累处理方法暗含了目标在处理时间内仅处于一个距离单元的假设。对于低信杂比目标，长时间的相参积累会导致目标跨越多个距离单元；对于高速目标，横跨距离单元(Across Range Unit,ARU)走动的问题会更严重[4–8]。此外，现代的高分辨雷达加剧了目标横跨距离单元走动的程度，传统相参处理方法面临着严重的性能下降问题。针对这些问题，长时间相参积累方法是一种有效的解决途径，如早期基于Keystone变换[9]、三维匹配滤波[10]的相关方法。不过这些方法处理流程比较复杂，且多采用级联处理校正ARU走动[11]。对于线性运动的目标，许稼等人[11]首次系统地提出了基于Radon傅里叶变换(Radon-Fourier Transform,RFT)的长时间相参积累方法用于解决动目标的ARU问题。作为广义的多普勒滤波器组，RFT方法的主要问题是存在盲速旁瓣和二维参数搜索计算量大[12,13]。为此，文献[12]提出提高距离分辨率、增加相参积累脉冲数或对多普勒滤波器权重加权可以抑制盲速旁瓣水平；文献[13,14]分别提出了基于快速傅里叶变换和粒子群优化算法的快速实现方法。针对RFT方法需要多维参数搜索的问题，文献[15,16]采用非搜索的参数估计方法，将慢时间(即脉间时间)信号时间反转再共轭相乘即可精确补偿距离弯曲和多普勒频移，但是这种方法会受多目标交叉项的影响。针对机动目标，文献[17]提出基于动态规划的相参积累方法，在不估计特定运动参数的情况下，积累任意运动目标的能量进行距离补偿和多普勒补偿；文献[18]针对速度恒定的曲线运动目标提出基于精确距离演化模型的广义RFT方法，不仅在不考虑目标速度和相干处理间隔的情况下进行有效的相干积分，还在多普勒域提供了额外的速度信息；文献[15]提出了一种基于慢时间反转变换和改进的RFT的高效相参积累方法，但如前文所述，该方法中的多目标交叉项会影响检测性能。

上述研究中所采用的信号模型都基于线性调频信号的理想匹配滤波结果，由于线性调频信号具有优良的多普勒容忍性(斜刀刃状模糊函数)，因此未考虑脉内多普勒频移的影响。实际上由于目标运动的影响，匹配滤波的峰值位置也会发生变化。如果发射的是相位编码信号等其他波形，则必须考虑脉内多普勒频移导致的主瓣展宽、幅度降低和位置误差。

本文结合现有研究分析了传统级联信号处理流程对高速目标能量积累不适应之处，从多维信号联合的角度提出联合脉压与Radon傅里叶变换的长时间相参积累方法。由于级联处理并非理论上的最优，该方法直接进行匹配滤波与RFT相结合的二重积分。实验表明联合脉压与Radon傅里叶变换的长时间相参积累方法在主瓣峰值的估计更加准确，不会出现级联处理那样的主瓣偏移，还能克服主瓣展宽、幅度降低等问题。

2 问题分析

传统雷达信号级联处理流程对高速目标能量积累的不适应可以从模糊函数与级联处理的结果两方面进行阐述。

2.1 根据模糊函数的角度分析

模糊函数不仅可以从距离-速度二维分辨力来定义，还可以从匹配滤波器的输出来定义。当信号s(t)具有多普勒频移时，其复包络为s(t)ej2πξt，假设此时匹配滤波器的响应函数未变，则对有多普勒频移的信号不再匹配。此时滤波器输出仍为时域卷积，

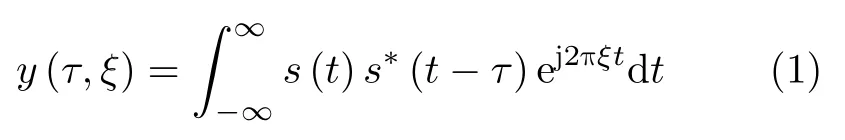
y(τ,ξ)则是模糊函数的另一种定义[19]。一些常用波形的模糊图如图1所示。线性调频(Linear Frequency Modulation,LFM)信号的脉宽100 µs，带宽0.2 MHz，采样频率1 MHz，上升斜率；非线性调频(Nonlinear Frequency Modulation,NLFM)信号参数与之一致并通过汉明窗调制；P3和P4码信号脉宽100 µs，码长5 µs，采样频率1 MHz。图1(c)、图1(d)、图1(g)、图1(h)是模糊图位于多普勒频率5 kHz处的切片，线性调频信号的脉压输出只在峰值位置有轻微误差；非线性调频信号的脉压输出峰值位置有误差且存在主瓣展宽；P4码信号的脉压输出存在严重的主瓣展宽、增益下降、旁瓣增高的问题，尤其是主瓣增益下降3 dB以上；P3码信号的脉压输出不仅存在以上问题，还有更严重的主瓣畸形的问题。当邻近单元存在多目标干扰时，P3和P4码信号更容易受到影响。

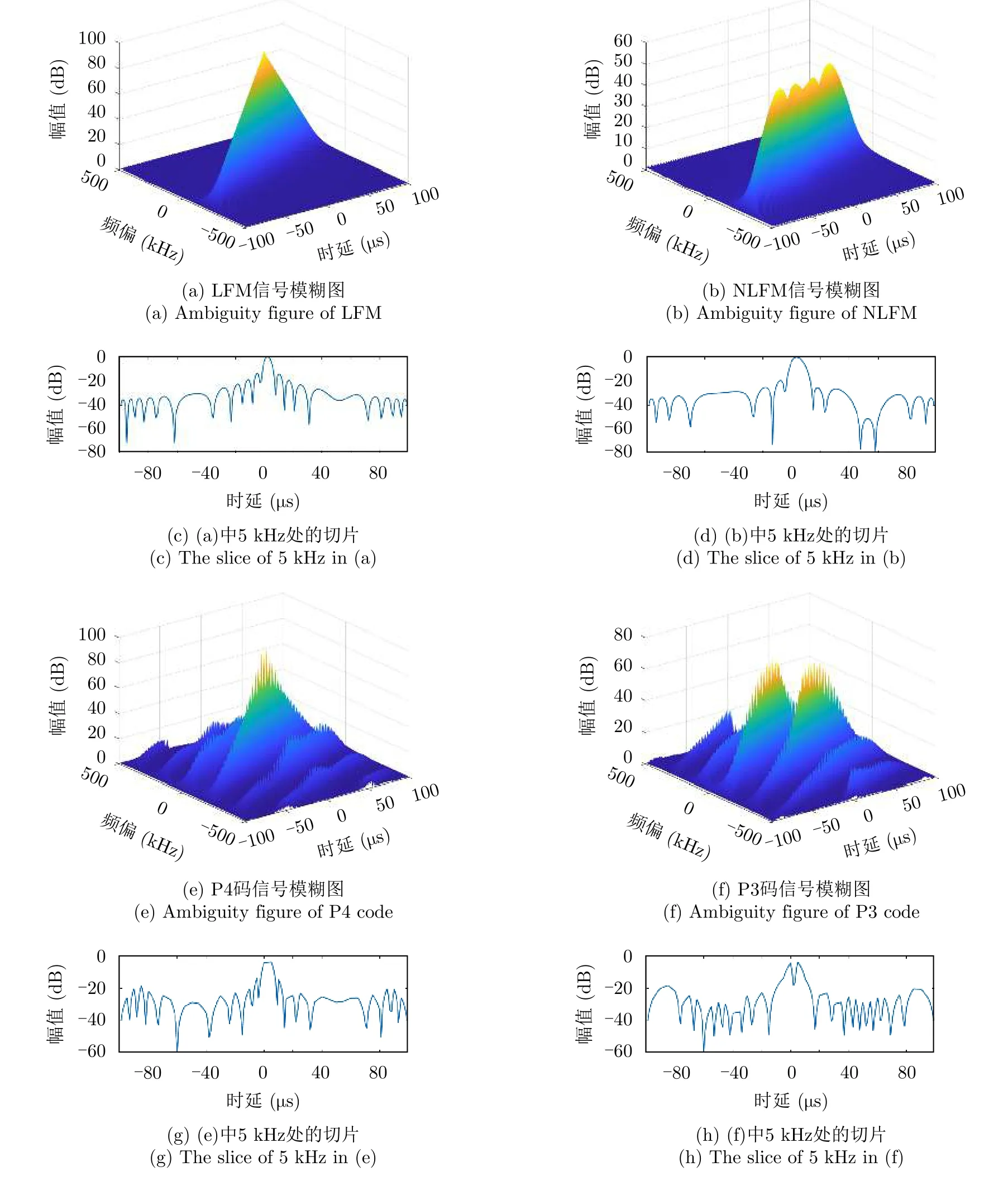
图1 LFM信号，NLFM信号，P4和P3编码信号的模糊函数Fig.1 Ambiguity figure of LFM,NLFM,P4 and P3 code

2.2 根据级联处理结果的角度分析

联合脉冲压缩与相参积累的必要性也源自于对高速目标的雷达回波进行脉冲压缩以及相参积累的级联处理时的性能退化。假设雷达发射信号矢量为s，脉宽为Tp，脉冲重复间隔(Pulse Repetition Interval,PRI)为TPRI。如图2所示高速目标在时长为T的相干处理间隔(Coherent Processing Interval,CPI)内发生横跨距离单元走动记为(t)[11]

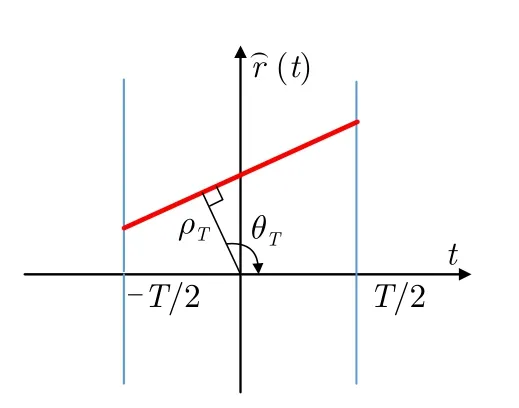
图2 目标横跨距离单元的走动Fig.2 The ARU walk of a target

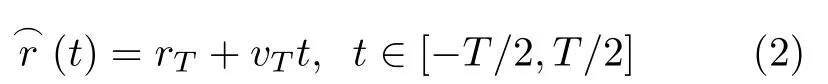
式中，rT为目标在0时刻所在的位置，vT是目标相对于雷达的径向速度，t是在CPI内的时间变量。

在时间T内雷达接收回波y可表示为

y是N个行向量组成的矩阵，表示T内N个脉冲重复间隔的回波数据，NT/TPRI。x为目标反射的回波信号所组成的矩阵，n为噪声、杂波和干扰的总和组成的矩阵。

级联处理首先对接收到的目标回波脉冲数据y进行匹配滤波，得到二维的匹配滤波输出表示为矩阵xpc，其中

匹配滤波之后，动目标检测(Moving Target Detection,MTD)以脉压结果xpc作为理想输入，但显然MTD处理并没有利用目标的速度信息。RFT方法能够搜索目标的运动参数实现目标能量的积累。

根据ARU走动在时间-距离二维笛卡儿坐标表示形式以及相应的极角-极径二维极坐标表示形式，

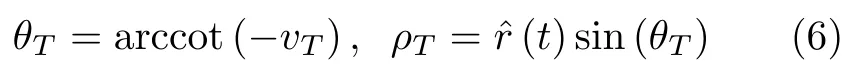
RFT共4种形式[11]，此处选择距离与速度的二维参数空间表示其连续形式为[20,21]

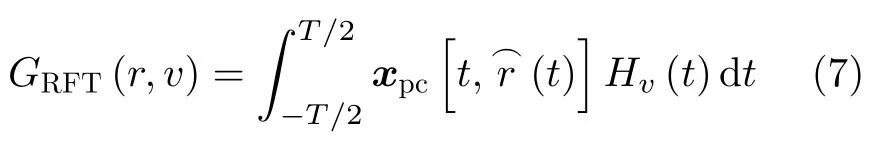
其中，Hv(t)是多普勒滤波器组[22,23]，

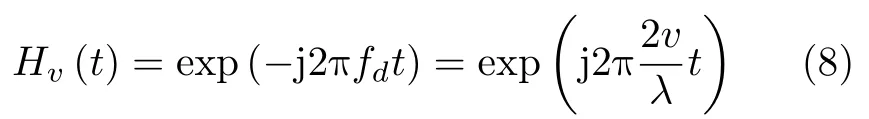
λ为波长，fd–2v/λ是目标的多普勒频率。实际情况下，RFT的速度参数取值限制在v∈[–vmax,vmax]。速度的遍历搜索较为复杂，如果用速度区间Δv将速度v的搜索空间离散化[24,25]，

则速度遍历Nvround(2vmax/Δv)即可。同时假设目标的运动范围为r∈[–rmax,rmax] (rmaxvmaxT/2)，根据雷达回波数据的采样情况，距离按照Δrc/(2fs)(fs为采样频率，c为光速)进行离散化，则距离遍历Nrround(2rmax/Δr)即可。因此RFT的离散形式表示为[26–28]

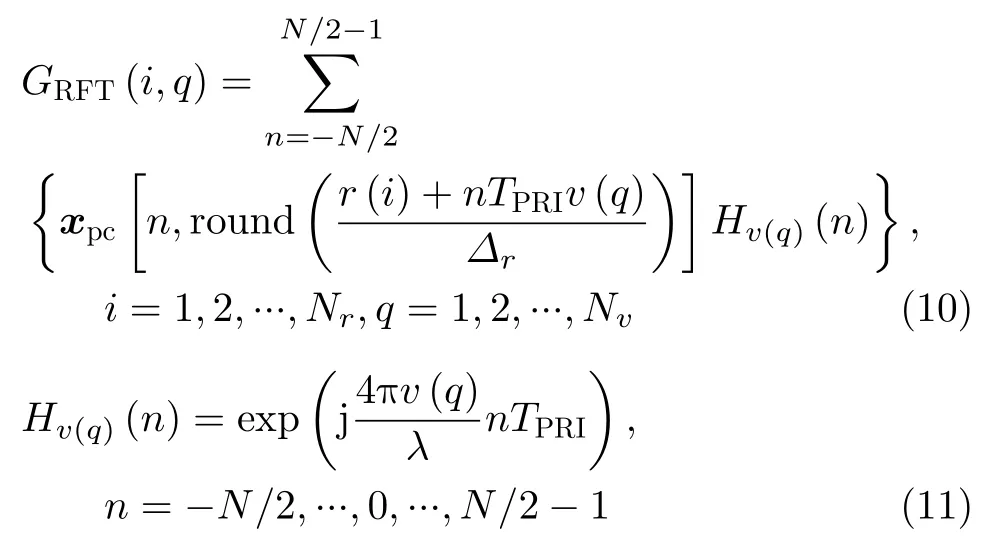
其中，i和q分别作为距离和速度的离散变量。RFT一般采用线性调频信号，以往的研究没有过多考虑脉内多普勒频移对脉压的影响。实际脉内多普勒频移仍然会影响线性调频信号的RFT输出，只是被忽略了。假设某S波段雷达载频为3 GHz，脉冲重复间隔TPRI0.005 s。信号带宽6 MHz，脉宽100 µs，调频为上升斜率，采样频率为30 MHz。一信噪比为10 dB的目标以–340 m/s的速度朝向雷达运动(本文速度的负值代表朝向雷达的方向)，0时刻该目标位于距雷达150 km处。在T为0.2 s(N40)的情况下进行级联处理。

CPI内的脉压结果如图3所示。由于目标发生ARU走动，匹配滤波处理后可以明显地看到目标的距离维峰值呈现出一条斜线。MTD处理后则无法得出目标位置与速度信息。即使是匹配滤波器和傅里叶变换联合的PC-FT方法，

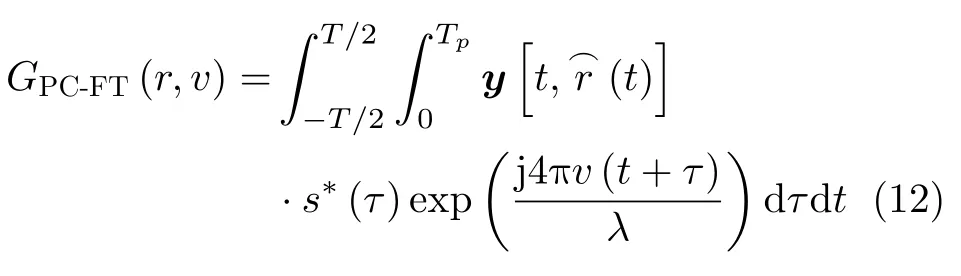
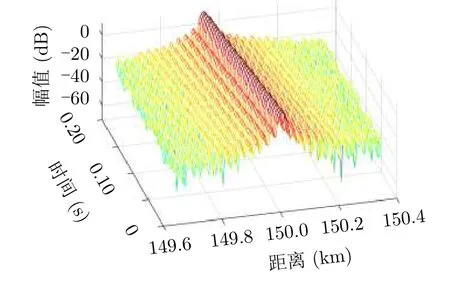
图3 0.2 s时间内的脉压结果Fig.3 The pulse compression result in 0.2 s

也会由于匹配滤波和傅里叶变换都是线性运算，导致PC-FT方法也和脉压与MTD的级联处理结果一致，无法将跨距离单元的目标能量积累起来。根据图4，目标在相干处理间隔内发生了ARU走动使得多个距离单元与多普勒单元处都存在峰值。

给定目标速度上限vmax550 m/s所得到的RFT处理结果则如图5所示。相比图4，图5(a)中脉压与RFT的级联处理具有更好的增益[11]。但是从图5(b)所示的–340 m/s的目标速度切片可知在脉压与RFT的级联处理下，目标的峰值位置偏移了150 km，因此对位置的估计是不准确的。

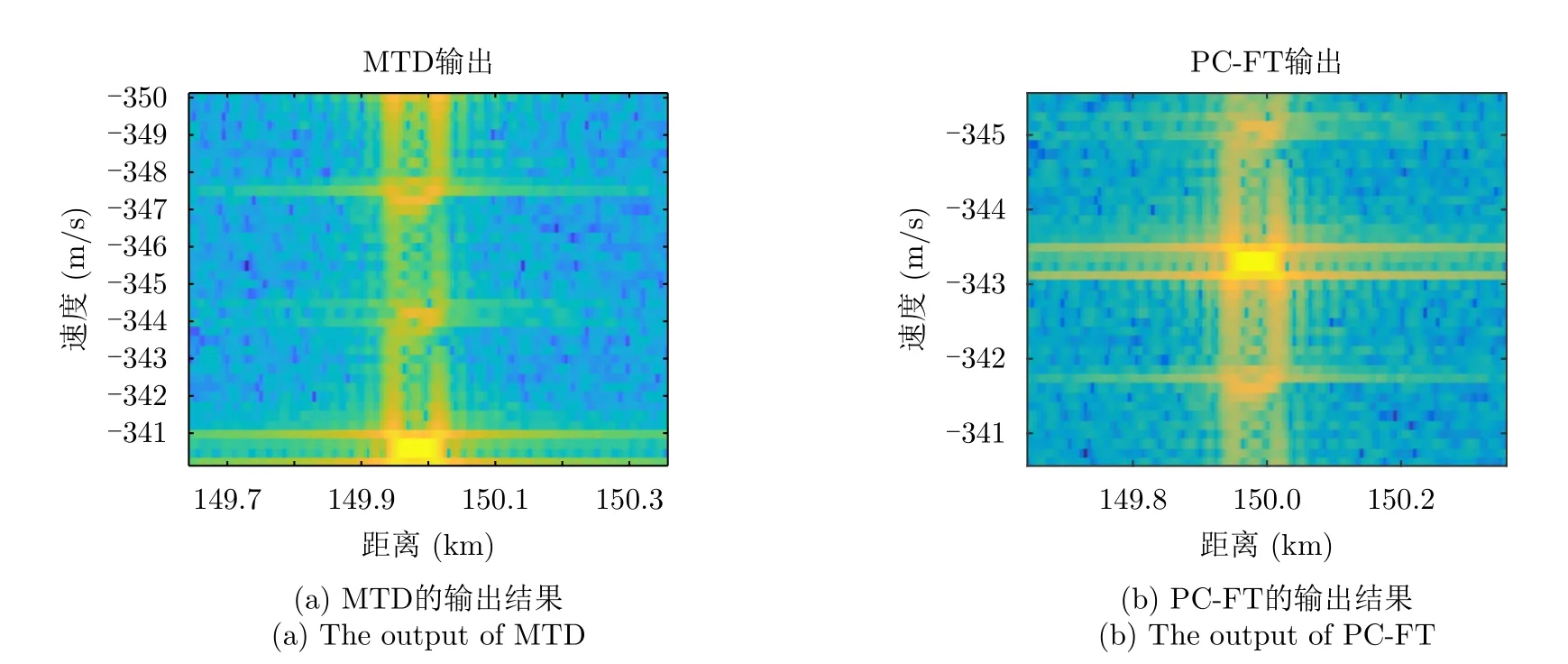
图4 MTD与PC-FT的输出结果Fig.4 The output of MTD and PC-FT

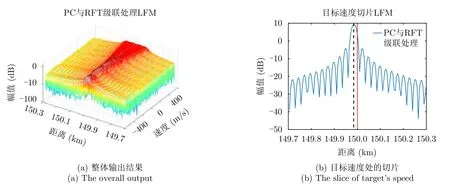
图5 脉冲压缩与RFT级联处理输出结果Fig.5 The output of cascaded processing

线性调频信号虽是目前十分常用的雷达波形，但也有大多数雷达使用非线性调频信号以及P3码、P4码等相位编码信号或是其他信号波形以达到较低脉压旁瓣的目的。而高速目标的脉内多普勒频率会对其他波形的级联处理产生更加严重的影响效果。非线性调频信号虽然没有出现较大的能量损失，但是主瓣位置出现了一定的偏移。P3码、P4码等相位编码信号虽然在目标没有高速运动的情况下可以得到更好的长时间相参积累效果，但是一旦存在因目标高速运动带来的失配就会出现明显的旁瓣抬升，主瓣偏移以及增益下降。

3 联合脉压与Radon傅里叶变换的长时间相参积累

经过第2小节的分析可得，无论采用任何一种信号波形对高速目标回波进行长时间相参积累时必须要考虑脉内多普勒频移对脉压的影响，即需要长时间时距联合处理。

3.1 PC-RFT的连续表示形式

脉压与Radon傅里叶变换的二维联合方法需要在脉压时就补偿目标的脉内多普勒信息，在回波信号与发射信号逐个元素卷积的同时进行Radon傅里叶变换从而构成二重积分。根据ARU走动在时间-距离二维笛卡儿坐标表示形式以及相应的极坐标表示形式，PC-RFT也具备4种连续表示形式。

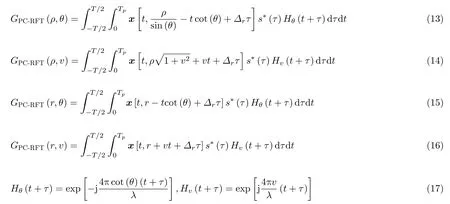
其中，ρ和θ分别表示目标运动轨迹相对于场景中心的极径和极角。Tp表示脉冲持续时间，t为慢时间(即脉间时间)，τ为快时间(即脉内时间)，s(τ)为波形在快时间τ时的采样值，∗表示取共轭运算。

以(r,v)域为例，将式(7)与式(16)进行对比，相比式(7)将匹配滤波输出作为理想脉压输出而忽略了多普勒滤波器组在脉内这段时间的相位变化，式(16)中直接引入了快时间变量τ，在匹配滤波器中每一个对应元素相乘时都引入与之对应的慢时间-快时间二维多普勒滤波器组Hv(t+τ)。因此PC-RFT方法在慢时间(时间)维与快时间(距离)维同时补偿多普勒频移。

3.2 PC-RFT的离散表示形式

与连续表示形式对应，PC-RFT方法的离散表示形式为

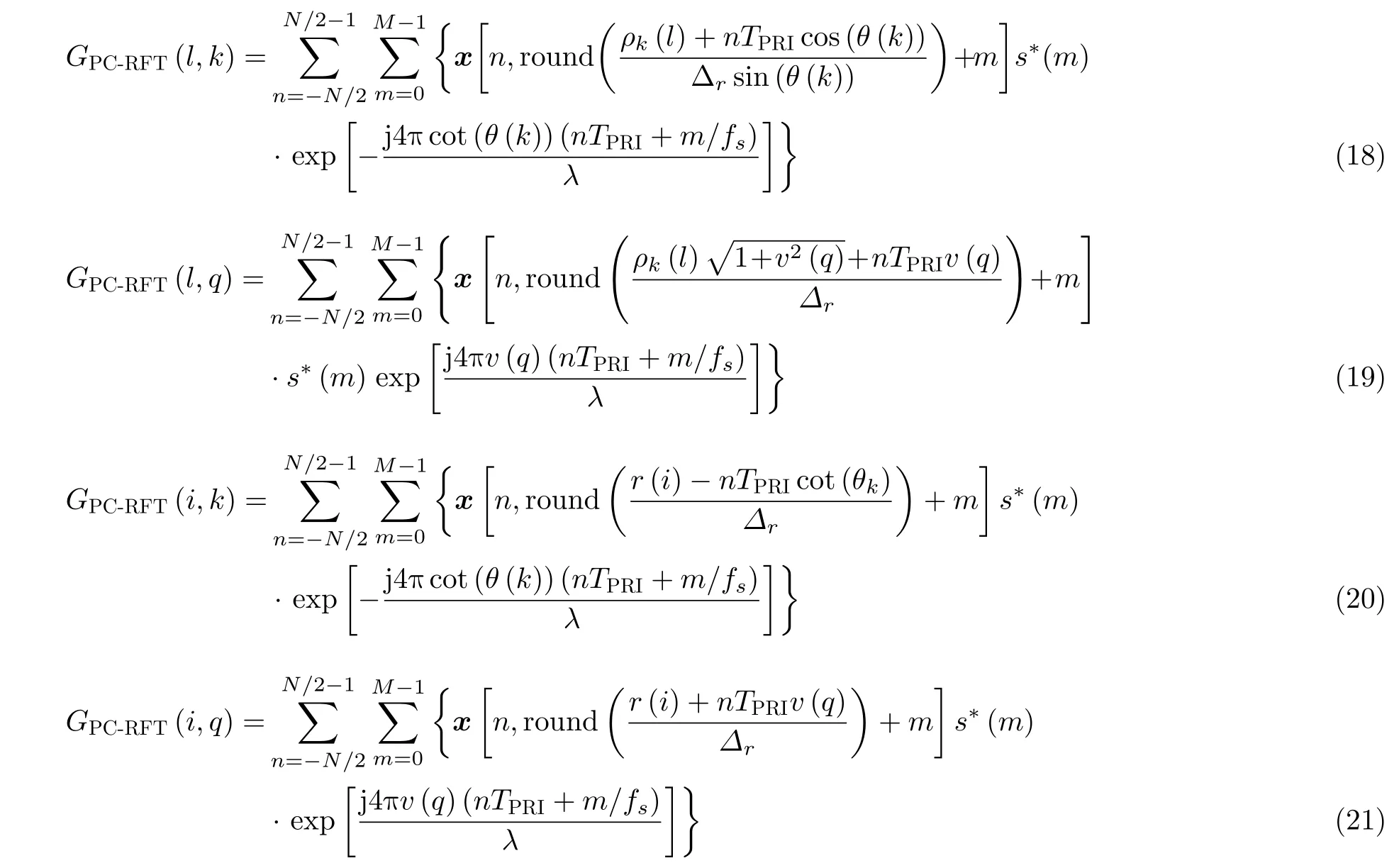
其中，i和q分别是对应于r和v的离散变量，l和k分别是对应于ρ和θ的离散变量，θ(k)arccot(–v(k)),ρk(l)r(l)sin(θ(k))且i,l1,2,···,Nr，同时k,q1,2,···,Nv。Mfsτ为脉冲内的采样点数，s(m)为波形的第m+1个采样值，fs为采样频率。为节省篇幅，本文主要考虑在距离与速度二维参数空间的离散表示形式。如果将PC-RFT与RFT方法的离散表示形式进行对比，可将式(10)重写为

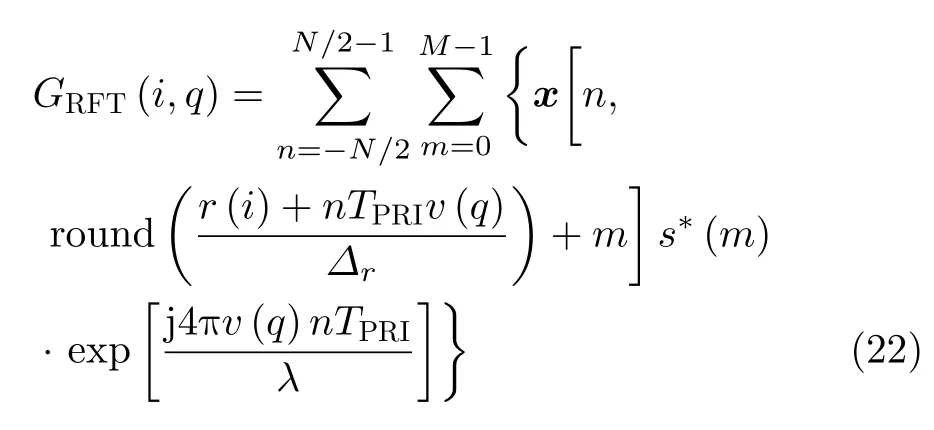
式(21)与式(22)对比可以明显看出二者之间相差exp[j4πv(q)m/fs/λ]。RFT方法缺失了该项则不能称为理论最优，因此PC-RFT方法才作为理论最优，在现实中比RFT方法更接近所能达到的理论最大增益。

3.3 计算量分析

PC-RFT算法在两个维度进行了运动补偿与能量积累，相比于RFT算法具有额外的运算量，因此本小节对算法运算量做出简要分析。以(r,v)域的表示形式为例，根据式(8),RFT算法所需要的运算量[11,13]为NrNv[NIm,c+(N–1)Ia,c]，其中NrNv表示对距离、速度的二维搜索，NIm,c+(N–1)Ia,c表示的是距离和速度搜索单元确定的情况下在PRI内的累加运算量，Im,c表示复数乘法，Ia,c表示复数加法。本文所提的PC-RFT算法一共需要NrNv(N–1)Ia,c[M2Im,c+(M–1)Ia,c]的运算量，其中NrNv仍然表示对距离、速度的二维搜索，(N–1)Ia,c表示在慢时间域所作的累加运算，M2Im,c+(M–1)Ia,c表示在快时间域所作的乘积与累加运算。由此可见PC-RFT算法的运算量确实要高于常规先脉压再进行RFT算法的运算量。

3.4 算法适用性讨论

正如RFT方法中所讨论的[11,13]，真实情况下，目标会存在做高阶运动(如加速度、切向运动等)的可能。高阶运动目标对RFT以及PC-RFT方法的影响需要通过合理的控制积累时间T以保证长时间相参积累的增益[11]。在积累时间有限的前提下，PCRFT方法同RFT方法一样无法补偿非线性距离走动，机动或变速目标的能量需要限制在单个距离-速度单元内，因此在时间T内PC-RFT方法仅允许径向速度在速度分辨单元内变化，否则将会产生横跨多普勒单元的走动，不利于PC-RFT方法对目标能量的积累。

4 仿真说明

为了验证联合脉压与Radon傅里叶变换的长时间相参积累方法的性能，本节继续假设某S波段雷达载频为3 GHz，脉冲重复间隔TPRI0.005 s。信号带宽6 MHz，脉宽100 µs，采样频率为30 MHz，对不同的信号波形的回波分别采用级联处理与联合处理并进行方法之间的性能对比。

4.1 单目标场景实验

在相干处理间隔T为0.4 s(即N80)的情况下设置vmax550 m/s。场景中心为150 km。场景能量积累范围Ra600 m，所以RgRa+vmaxT820 m。另外Δr5 m，Nr120且Δv0.2 m/s，Nv5500。一信噪比为0 dB的目标在距离雷达150 km处(场景中心)以vT300 m/s的速度远离雷达运动。如不特别说明，本小节的仿真均采用以上参数设置。

4.1.1 对线性调频信号回波的处理

本小节线性调频波形采用上升斜率。对80个脉冲做匹配滤波所得到的脉冲压缩输出结果如图6所示。图6(a)的全局脉冲压缩输出可以明显显示出目标在该时间段内所做的ARU走动。但是图6(b)中0时刻脉压的主瓣位置已经偏离了150 km的位置，再一次说明脉内多普勒频率影响了脉冲压缩的性能。级联信号处理流程中，上一级流程没有做到最优处理，势必会影响下一级流程。

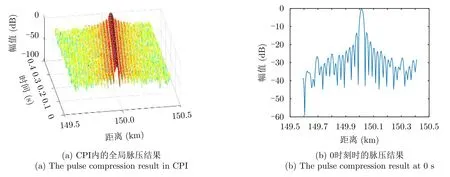
图6 线性调频信号回波的匹配滤波脉压输出Fig.6 Matched filter output of LFM

级联处理与联合处理结果如图7所示。直观看二者的区别并不十分明显，都在目标所在的大致范围处积累了能量且速度维旁瓣比较明显。但是将速度为300 m/s的切片进行对比，如图8所示。两种方法的目标主瓣增益基本没有区别。将速度切片中目标主瓣与第一副瓣的比值作为主副比，则级联处理结果主副比为13.38 dB，联合处理结果的主副比为13.39 dB，虽然两种方法的主副比基本没有差别，但是PC-RFT处理直接克服了目标主瓣的偏移问题，与级联处理的结果之间存在显著的区别。

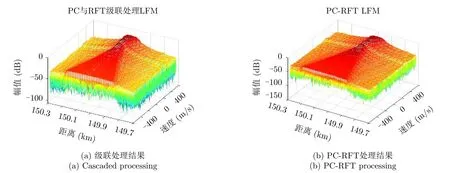
图7 两种方法对LFM信号回波的处理结果Fig.7 The result of the two methods (LFM)

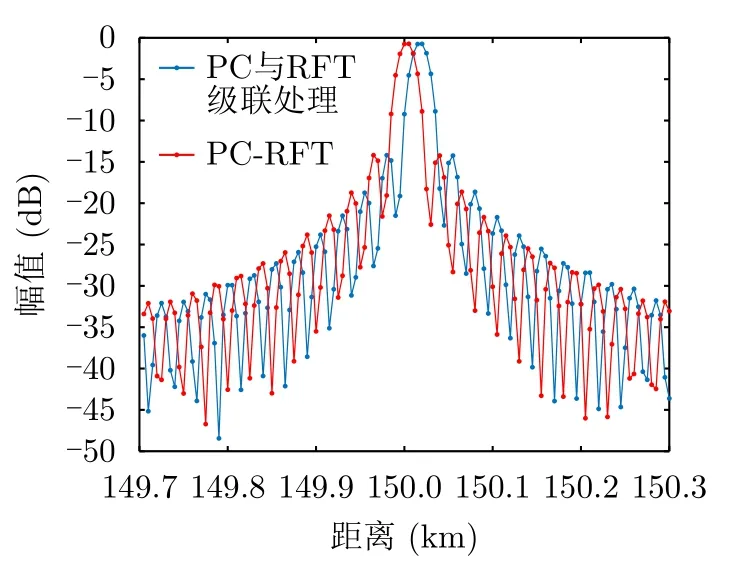
图8 目标速度切片(LFM)Fig.8 The slice of target’s speed (LFM)

4.1.2 对非线性调频信号回波的处理

本小节所采用的非线性调频波形是通过4次余弦窗函数cos4(0.7πf/B)设计幅度谱，再利用相位驻留法计算相位函数而得的[29,30]。匹配滤波所得到的脉冲压缩输出结果如图9所示。图9(a)可显示出目标在时间T内的ARU走动。图9(b)所示0时刻脉压中已经不仅存在主瓣偏移，还存在一定程度的主瓣展宽和旁瓣抬升。

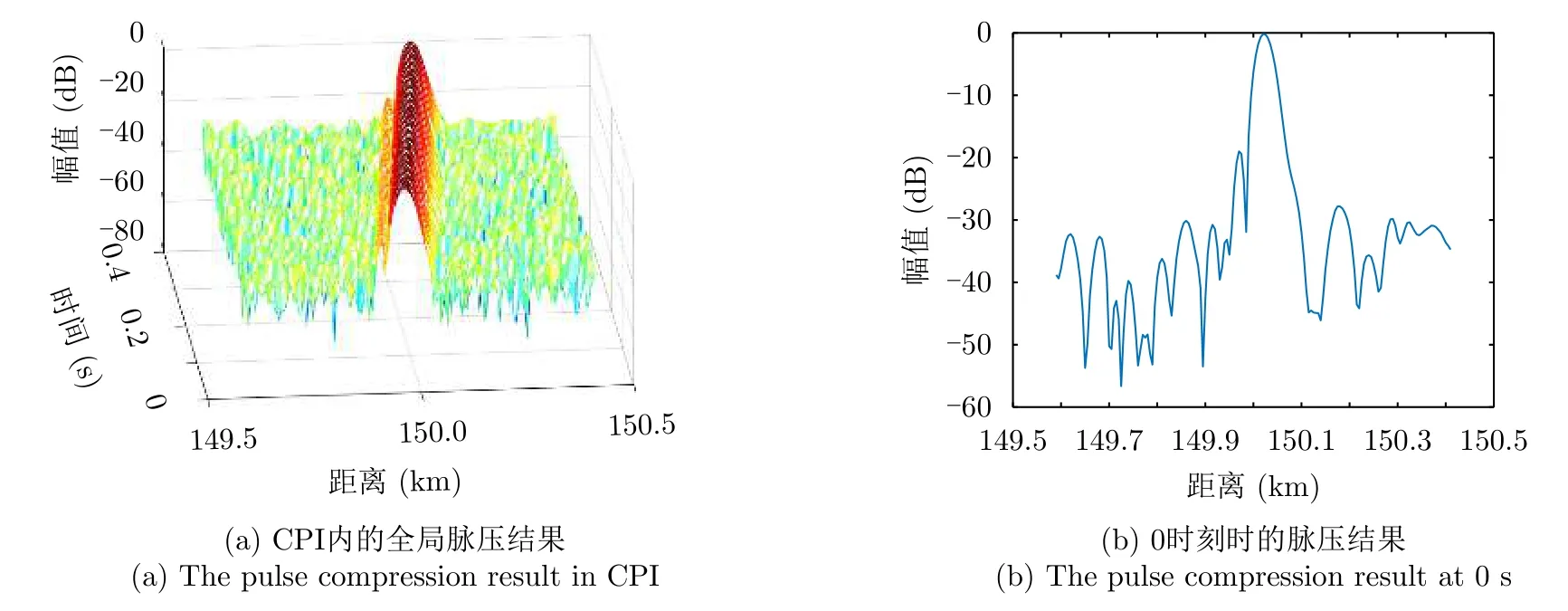
图9 非线性调频信号回波的匹配滤波脉压输出Fig.9 Matched filter output (NLFM)

非线性调频信号回波的级联处理与联合处理结果如图10所示。虽然二者输出的速度维旁瓣比较明显，但在目标周围的距离旁瓣也已经有明显区别，PC-RFT的目标距离旁瓣明显低于级联处理。在图11目标速度切片对比中，级联处理结果主副比为20.63 dB，联合处理结果的主副比为39.29 dB，可见PC-RFT处理直接克服了目标主瓣的偏移问题，以及主瓣展宽与旁瓣抬升的问题。

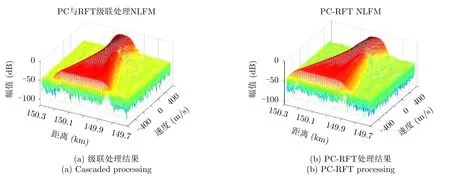
图10 两种方法对NLFM信号回波的处理结果Fig.10 The result of the two methods (NLFM)

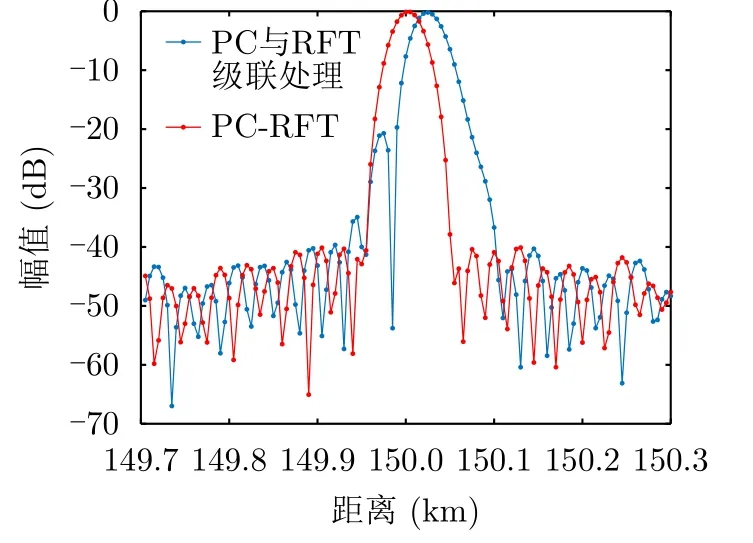
图11 目标速度切片(NLFM)Fig.11 The slice of target’s speed (NLFM)

4.1.3 对P4码信号回波的处理

本小节所采用的P4码信号波形(s(n)exp(jπn·(n–Nc)/Nc),n0,1,···,Nc–1,Nc为信号码数)码长为0.1 µs。匹配滤波所得到的脉冲压缩输出结果如图12所示。图12(a)为目标在时间T内所做的ARU走动。图12(b)中不仅存在主瓣偏移、主瓣展宽和旁瓣抬升的问题，还伴随有主瓣能量衰减。

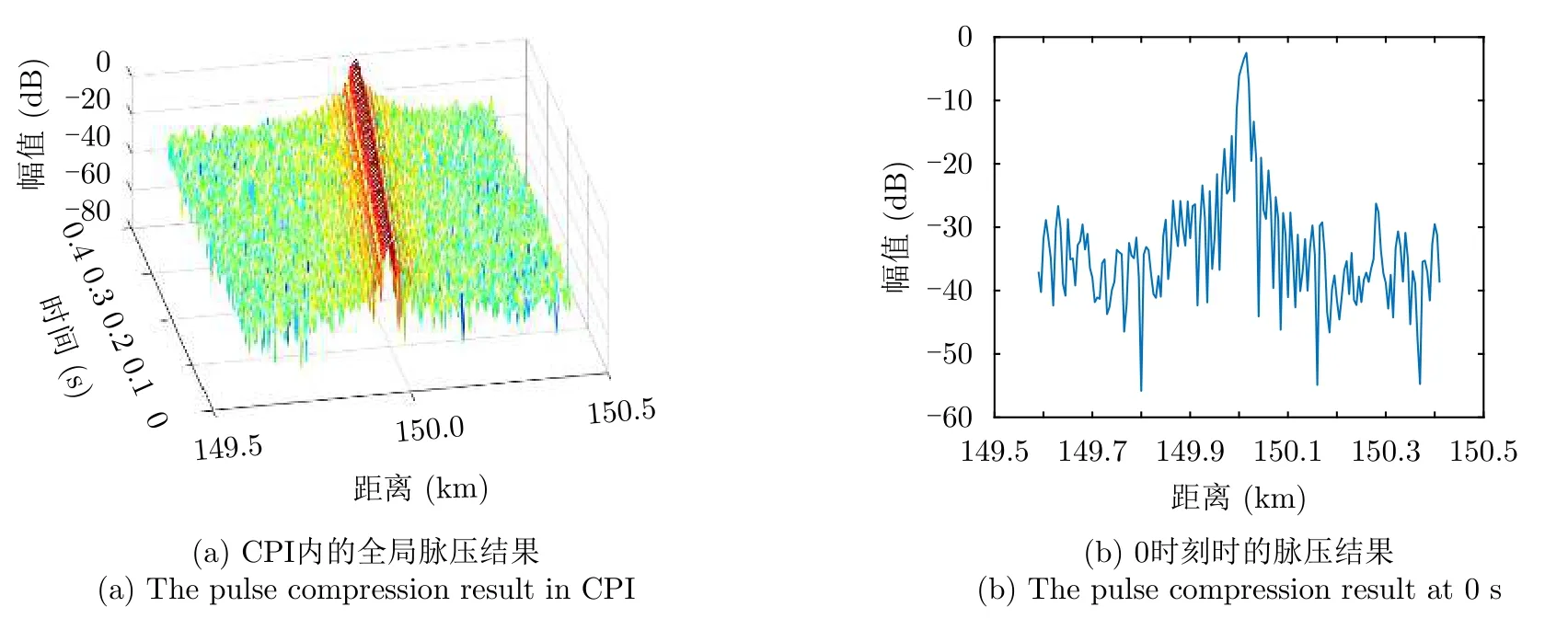
图12 P4码信号回波的匹配滤波脉压输出Fig.12 Matched filter output (P4)

P4码信号回波的级联处理与联合处理结果如图13所示。

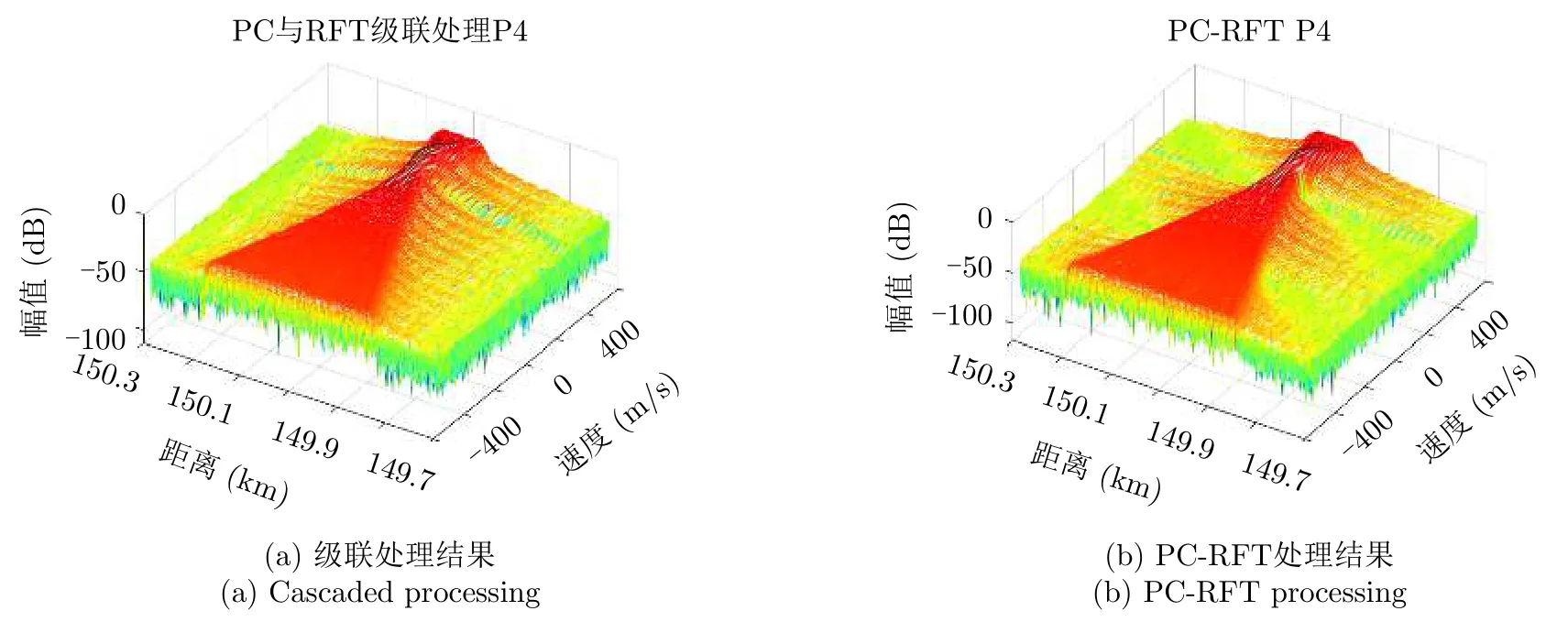
图13 两种方法对P4码信号回波的处理结果Fig.13 The result of the two methods (P4)

由于相位编码信号对多普勒频率的敏感性，对P4码信号级联处理与联合处理的区别较为明显，尤其是距离旁瓣明显存在差异，PC-RFT处理得到的距离旁瓣要明显低于级联处理。具体区别如图14所示，PC-RFT处理直接克服了目标主瓣的偏移问题，以及一定的主瓣展宽。更明显的：一是级联处理结果主副比为12.72 dB，联合处理结果的主副比为43.31 dB,PC-RFT处理有效解决了级联处理P4码信号回波时的旁瓣抬升问题，二是级联处理中目标主瓣衰减了约2.9 dB,PC-RFT处理虽然也存在衰减1.4 dB的情况，但在一定程度控制了能量的衰减。

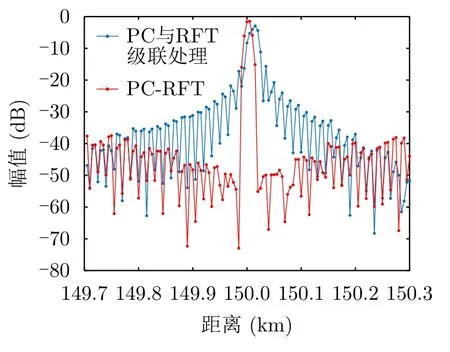
图14 目标速度切片(P4)Fig.14 The slice of target’s speed (P4)

4.1.4 对P3码信号回波的处理

本小节所采用的P3码信号波形(s(n)exp(jπn2/Nc),n0,1,···,Nc–1,Nc为信号码数)码长同样为0.1 µs。在目标处于场景中心以vT300 m/s运动的过程中，对80个脉冲做匹配滤波所得到的脉冲压缩输出结果如图15所示。图15(a)仍可明显地显示出运动目标在该时间段内所做的横跨距离单元走动。图15(b)中也存在主瓣偏移、展宽、能量衰减和旁瓣抬升的问题。与前3种情况稍不同，本小节的主瓣和旁瓣的对比关系变化尤其明显。

P3码信号回波的级联处理与联合处理结果如图16所示。此处距离旁瓣明显存在差异，PC-RFT处理得到的距离旁瓣要明显低于级联处理。具体如图17所示，PC-RFT处理直接克服了目标主瓣偏移和主瓣展宽的问题。更明显地：一是相比级联处理的目标主瓣衰减了约3.5 dB,PC-RFT处理虽也存在衰减1.4 dB的情况，仍然在一定程度上控制了能量的衰减。二是级联处理结果主副比为3.47 dB，联合处理结果的主副比为42.17 dB,PC-RFT处理解决了级联处理P3码信号回波时稍有不同的旁瓣抬升问题。无论是根据图15(b)还是图17，级联处理的结果出现了近似两个目标峰值的情况。这种情况会严重影响后续的目标检测等信号处理流程。而PC-RFT的联合处理明显克服了该问题，抑制了距离旁瓣，为后续流程提供了更好的处理结果。

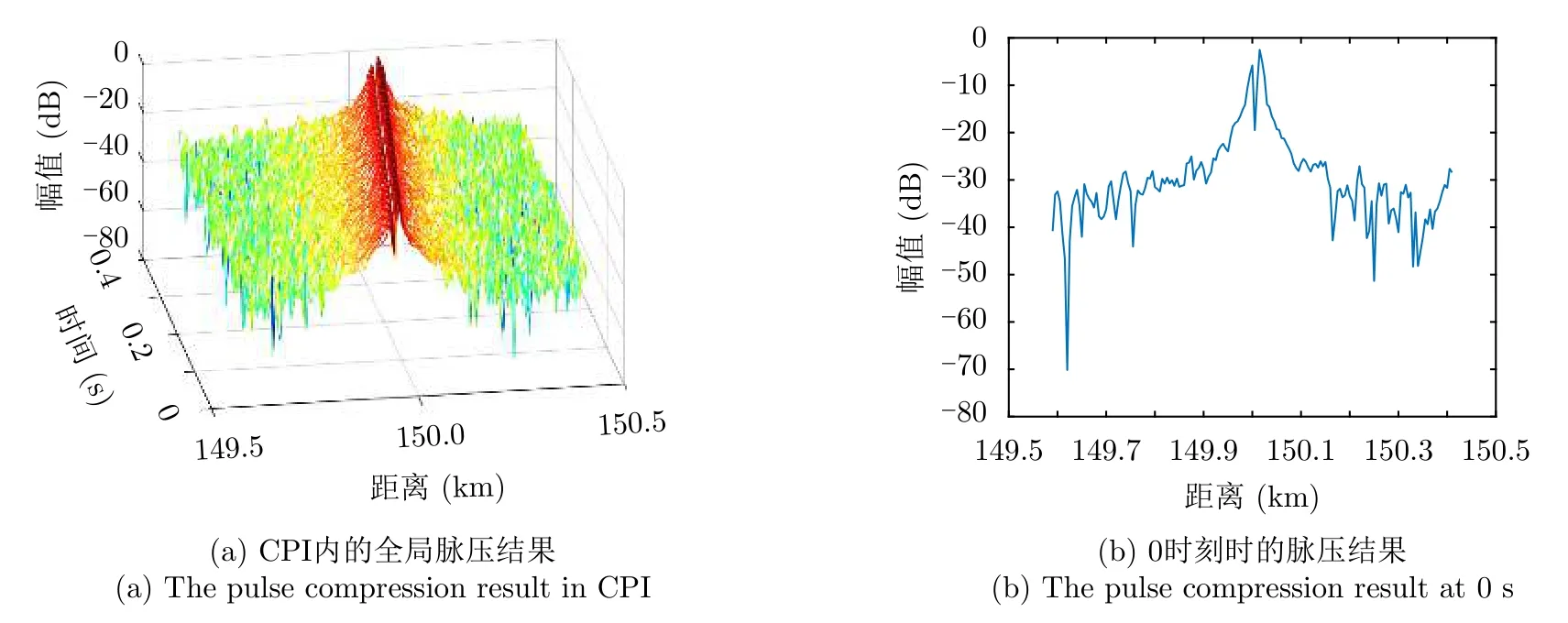
图15 P3码信号回波的匹配滤波脉压输出Fig.15 Matched filter output (P3)

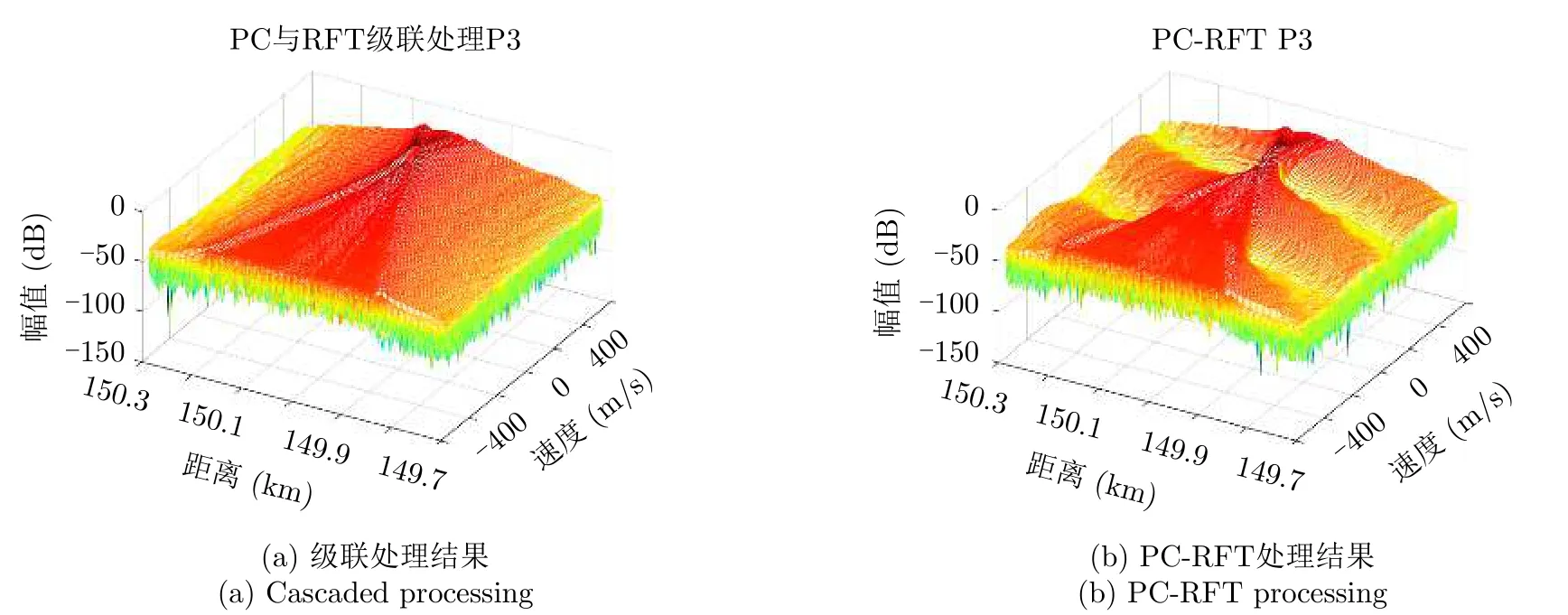
图16 两种方法对P3码信号回波的处理结果Fig.16 The result of the two methods (P3)

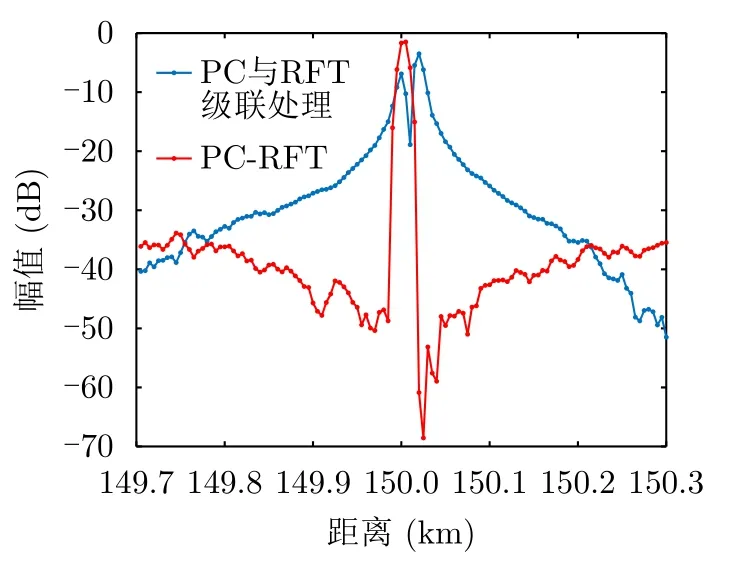
图17 目标速度切片(P3)Fig.17 The slice of target’s speed (P3)

4.2 多目标场景实验

在相干处理间隔T为0.4 s的情况下设置vmax1200 m/s。场景中心为150 km。场景能量积累范围Ra600 m，所以RgRa+vmaxT1080 m。微弱目标增程探测主要基于线性调频信号波形，因此本小节实验只针对线性调频信号波形。两个信噪比为–10 dB的目标在距离雷达150 km和150.05 km处以3倍声速远离雷达运动，另有两个信噪比为–2 dB的目标在距离雷达150 km和150.05 km处以500 m/s的速度运动。PC-FT,PC与RFT级联处理,PCRFT方法的输出结果如图18—图20所示。在PCFT的输出中由于存在多普勒模糊，所以图18的纵坐标没有与目标的速度对应。图18中目标的能量仍然分散在多个距离和多普勒单元，没有聚焦。

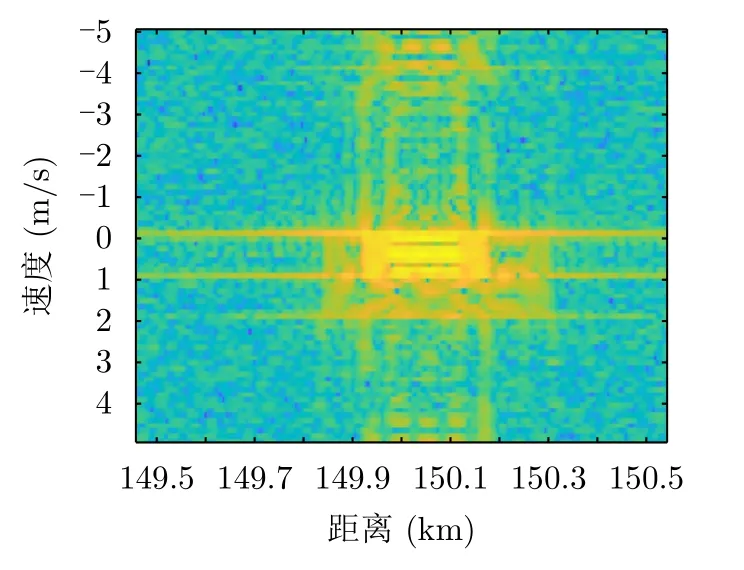
图18 PC-FT输出Fig.18 The output of PC-FT

图19和图20中，PC与RFT级联处理与PC-RFT方法都对4个目标的能量实现了较好的聚焦，且两种方法处理下的目标主瓣增益与主副比都基本相近。但由于级联处理没有补偿脉内多普勒，4个目标的主瓣位置都出现了偏移。而PC-RFT方法克服了4个目标主瓣的偏移，使得4个目标的主瓣位于正确的距离-多普勒单元上。

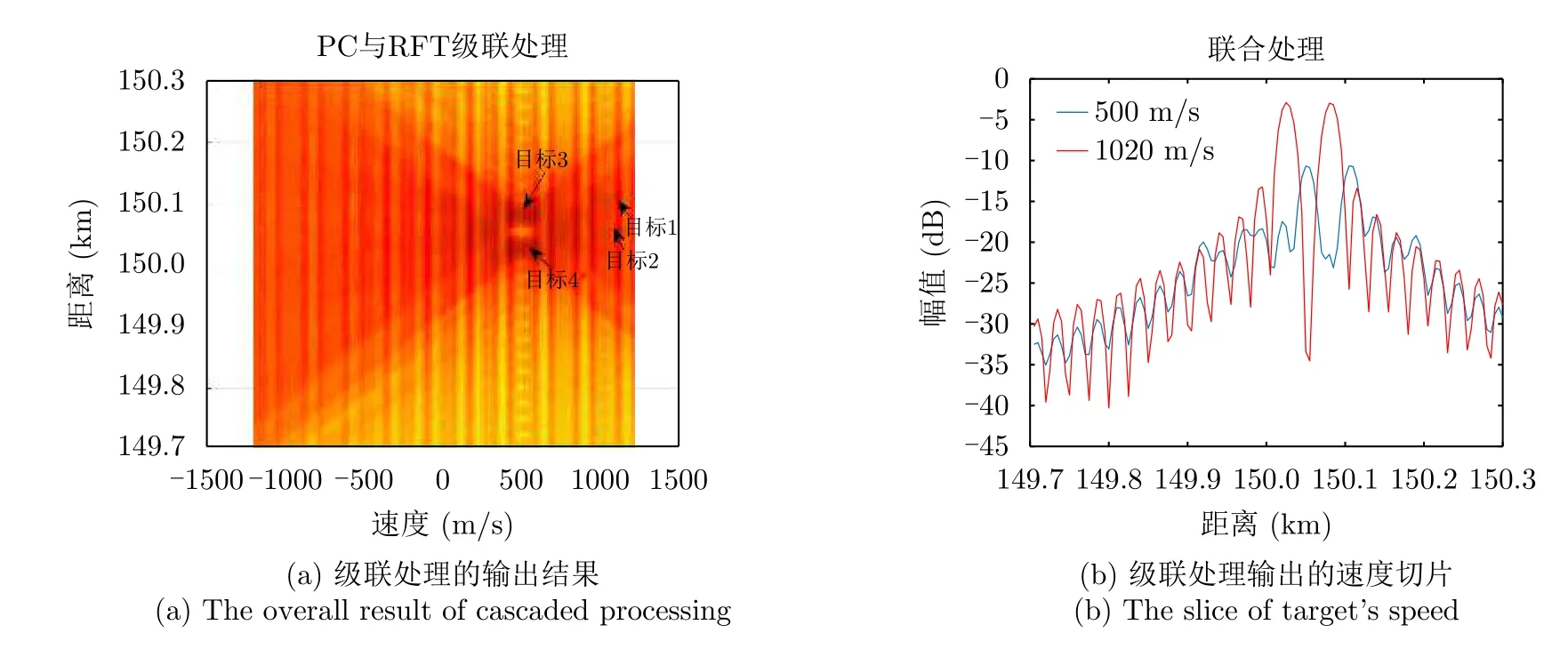
图19 PC与RFT的级联输出Fig.19 The output of cascaded processing (PC and RFT)

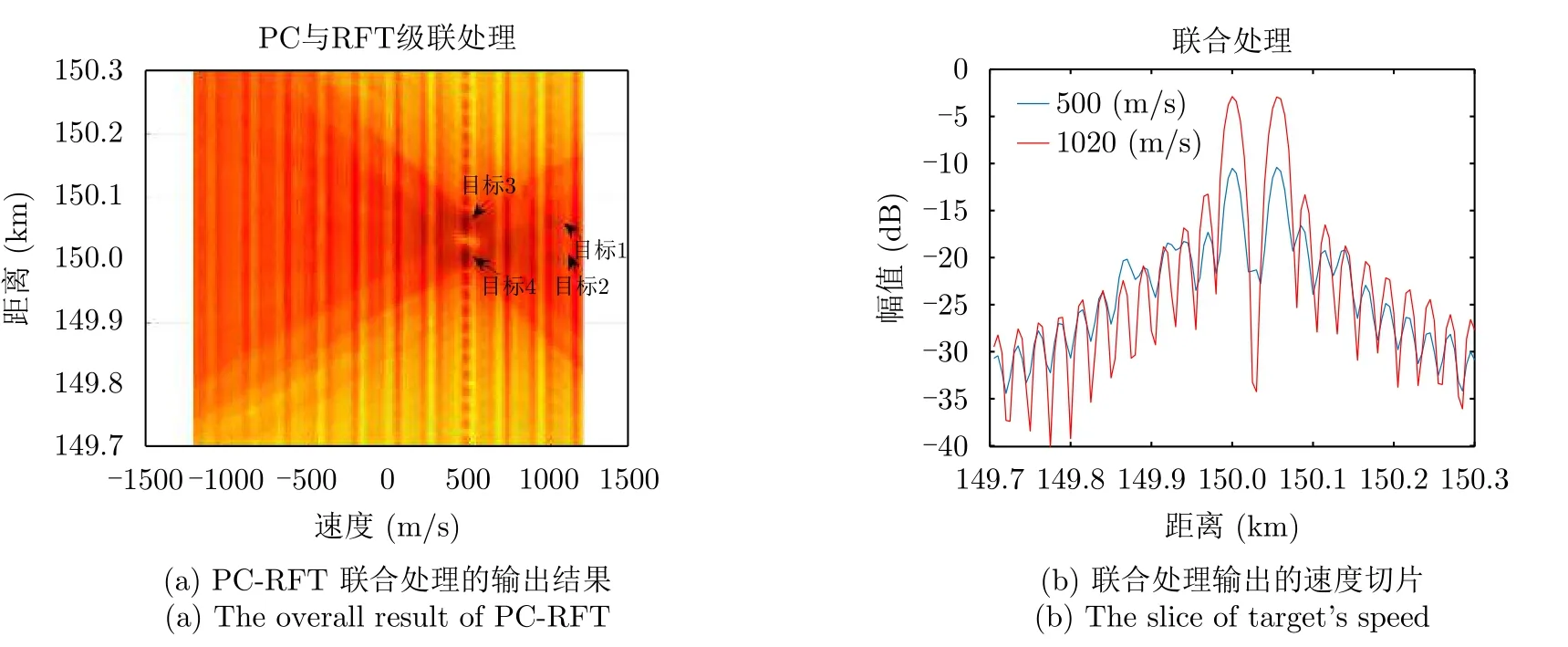
图20 PC-RFT的输出Fig.20 The output of PC-RFT processing

5 结论

本文结合已有研究分析了传统的级联信号处理流程对高速目标不相适应的地方，分析了应用几种当前常用的脉压波形在对高速目标回波的级联处理中造成的偏差，从多维信号联合的角度提出联合脉压与Radon傅里叶变换的长时间相参积累方法。其实在现今随着雷达分辨率的提升，对微弱目标进行长时间相参积累处理时，该问题便一直存在，只是目前大多数的研究都忽视了。虽然对于线性调频信号而言，对于目标增益的改善较小，但是明显地克服了目标主瓣的偏移。联合处理对多普勒敏感的非线性调频信号和相位编码信号波形的处理性能是显而易见的，不仅克服了目标主瓣的偏移，还解决了旁瓣抬升和主瓣能量衰减的问题。所以综合来看，联合处理明显优于级联处理。未来将着重研究可快速实施的联合处理方法以及引入目标高阶运动参数的联合处理方法。