考虑孔隙水压力作用下浅埋黄土隧道稳定性的上限分析

于 丽，吕 城，夏鹏曦，王明年

(1.西南交通大学 土木工程学院，四川 成都 610031；2.西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031)

随着西部大开发，西部交通正处于蓬勃发展时期，而我国西北地区分布着全球最为广泛、发育最为完整的黄土，不可避免地出现大量黄土交通隧道工程。浅埋隧道在施工过程中变形比较大，支护不当时容易发生坍塌事故，故浅埋隧道的稳定性分析是必不可少的。对浅埋隧道整体稳定性的研究，国内外学者已经取得了一些成果。如，Broms[1]应用极限平衡理论分析了浅埋隧道的稳定性，当稳定性系数小于6时土体基本稳定；郑颖人等[2]采用有限元法结合强度折减法对土体隧道围岩的稳定性进行了研究，并求取隧道的滑裂面；姜功良[3]将极限分析上限法和有限元法结合起来评价隧道的稳定性求解其稳定性系数，使得既有的上限分析结果得到了显著改善，并且很接近于极限分析下限法的结果，以此界定准确解的范围。Davis等[4]针对黏性土的浅埋隧道，采用极限分析法提出了不排水条件下隧道环向开挖面稳定的简单破坏模式，求出了隧道环向开挖稳定力的上下限解。文献[5-6]基于己有的直线型多块体破坏机制采用极限分析上限法求解隧道整体安全系数的上限解。上述研究只能适用于普通浅埋隧道，难以在浅埋黄土隧道中应用。

由于黄土的工程特性如垂直节理发育[7-9]，破坏了隧道围岩的完整性和连续性导致浅埋黄土隧道的破坏模式不同与其他普通土质隧道从而影响着隧道整体的稳定性，隧道开挖导致土体沿垂直节理面的软弱面发生坍塌破坏，因此浅埋黄土隧道的坍塌面大多是直立面[9-10]。黄土的水敏性强，地下水或降雨入渗对黄土的强度影响比较显著从而影响浅埋黄土隧道的稳定性[11-12]，目前研究浅埋黄土隧道稳定性的理论不够成熟。鉴于此，本文构建浅埋黄土隧道的二维有限多块体平动破坏模式，考虑孔隙水压力作用，结合极限分析上限法和强度折减法分析浅埋黄土隧道的稳定性，求得隧道整体安全系数的上限解及对应的滑裂面。将安全系数计算结果和文献[5-6]的研究、有限差分法进行对比，验证了本文方法的合理性；分析孔隙水压力及孔隙水压力作用下参数变化对隧道整体的安全系数及其破裂范围的影响。

1 强度折减法

强度折减法最初由Zienkiewicz提出[13]，通过有限元计算方法不断折减土体的强度使岩土体处于极限状态，此时对应的折减系数Fs即为安全系数，折减后土体的强度参数表示为

(1)

根据强度折减法原理，结合极限分析上限定理可求得隧道的安全系数。将土体参数c、φ除以折减系数Fs进行折减后代入机动速度场中的能耗计算中，得到含有折减系数的多个变量的目标函数，在速度场中的几何关系和速度矢量关系约束下采用序列二次优化迭代法对目标函数进行优化得到极限状态下的安全系数Fs，即是隧道整体的安全系数[13]。

2 孔隙水压力作用下的上限定理

孔隙水压力系数由Skempton[14]提出，可以通过三轴实验得出数值，Michalowski[15]将孔隙水压力视为一个作用在土体颗粒上的外力，文献[5-6]认为在上限分析中孔隙水压力使土体颗粒膨胀做的功和水压力在速度场边界上所做的功为孔隙水压力作的功。所以，孔隙水压力作用下的上限定理为

(2)

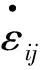
土体中孔隙水压力u可以视为上覆土层自重应力的一部分，所以孔隙水压力表达式为

u=ruγz

(3)

式中：ru为孔隙水压力系数；γ为土体的重度；z为地表以下任意点到地表的垂直距离。

忽略刚性块体中的体积应变，孔隙水压力做的功率全部由作用在破坏机制边界上的那一部分产生[5]，因此孔隙水压力功率Pu表达式为

(4)

3 浅埋黄土隧道围岩破坏模式

3.1 破坏模式构建

由于黄土垂直节理发育导致浅埋黄土隧道的破坏模式不同于其他普通隧道，隧道的稳定性也必然存在着差异，浅埋黄土隧道围岩首先在边墙或者墙脚发生破坏[16]，然后向上延伸至地表附近，浅埋黄土隧道坍塌面大多数接近为直立面[10]，故本文提出浅埋黄土隧道的二维刚性有限多块体平动破坏模式见图1，隧道断面采用郑西客专黄土大断面隧道的断面形式，隧道上方破裂面为直立型，下方是由三角块体组成。构建的破坏模式中竖向支护反力为q，水平支护反力为e=Kq；K为侧向土压力系数；隧道顶部圆弧半径为R也是跨度的一半，这里暂时只考虑地面水平的情况。

图1 浅埋黄土隧道的破坏模式

由图1可知，在本文假定的浅埋黄土隧道破坏模式下第i-1块和第i块三角形块体的边长和角度之间的关系，进而得到各个速度矢量之间的关系。这样就可以对各个滑块的几何参数以及速度矢量进行求解。求解过程中可以假定上方直立块的速度v1是一个不为0的任意值[17]。

3.2 计算过程

(1)几何关系

各个三角形的边长变化见图2，依据三角形的性质，各个边长的关系分别为

图2 几何、速度关系

(5)

(6)

(7)

FC=ED1=h

(8)

递推过程中，先计算CDi，再计算DiDi+1，然后依次可以计算出各个三角形块体的边长。

各块体的面积分别为

(9)

S0=FC·ED1

(10)

(11)

(2)速度矢量关系

根据图2，采用三角形的正弦定理可以得到如下的速度关系式

(12)

(13)

(14)

(15)

速度vi的方向角ψi(与竖直方向的夹角)为

ψ1=φ

(16)

(17)

(3)功率计算

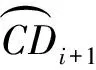
(18)

间断面上的内能耗散功率Pc为

ED1·v1]·cosφ

(19)

开挖面支护力的功率Pq为

Pq=2·q·R·v1+2·Kq·H·v1·sin(βi+φ)

(20)

地表荷载的功率Ps为

Ps=2·σs·CD1·v1

(21)

三角形边DiDi+1与竖直方向的夹角εi为

(22)

孔隙水压力做的功Pu为

Pu=-2·γ·rusinφ[h·CD1·v1+

(23)

即依据极限分析上限定理，内功率等于外功率

Pq+Pc=Pγ+Pu+Ps

(24)

已知破坏滑裂面的范围即已知的CDi+1长度时，则支护反力为

(25)

3.3 安全系数上限解的优化

根据前述讨论令折减后的极限支护力等于隧道实际的支护力q=q0，即可以求得安全系数Fs的目标函数f(α1,α2,…,αi,β1,β2,…,βi)。在本文破坏机制下的最优上限解是满足速度矢量关系的支护力最小值，在满足速度矢量相容的前提下需要结合序列二次优化迭代法对这个目标函数进行优化[6]。

首先确定求解问题的约束条件，再将其代入到Fmincon函数中，然后对初值进行合理的设置来求解具体给定的工程问题。利用数值计算软件Matlab进行编程，最终可以求解出破坏模式下安全系数的最优解[17]及其对应的破裂范围，本文中块体数量i=25。由速度场中的矢量关系可得到有约束条件下目标函数的数学规划表达式为

Fs=Fs(α1,α2,…,αi,β1,β2,…,βi,Fs)

(26)

式(26)中自变量因素条件为

(27)

4 计算方法合理性验证

为了检验本文构建的二维刚性有限多块体平动破坏模式结合有限分析上限法研究浅埋黄土隧道稳定性的适用性，为浅埋黄土隧道稳定性评价提供可靠的参考依据，下面将安全系数与已有研究方法进行对比分析。

4.1 研究方法验证

为了验证本文方法的正确性，将本文方法与文献[9]的研究进行对比，根据文献[9]取各参数分别为c=20 kPa，b=5 m，h=10 m，q=100 kPa，γ=20 kN/m3，地表荷载暂时忽略不计，θ=108°40′18″，φ=5°～30°时，比较两种方法计算浅埋隧道整体安全系数Fs随φ的变化情况见图3。

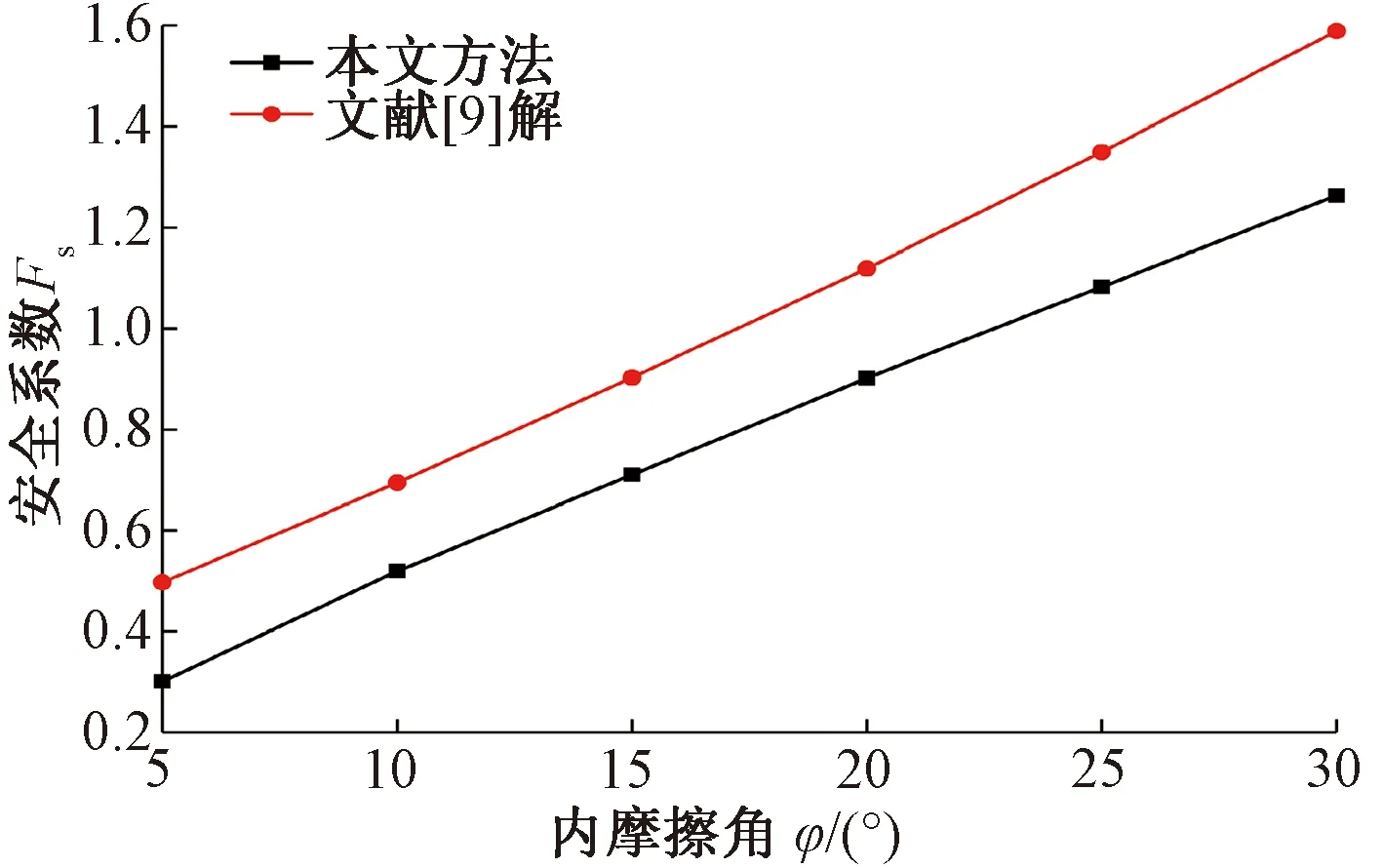
图3 浅埋黄土隧道安全系数计算对比

由图3可知，本文方法求解的浅埋隧道整体安全系数Fs与文献[9]解相差较小，本文方法求解得到的安全系数Fs比文献[9]解平均小24%左右，且安全系数Fs随内摩擦角的变化规律一致，同时由于黄土垂直节理发育破坏了围岩的完整性[6-7]导致浅埋黄土隧道的稳定性降低，说明本文方法求解浅埋黄土隧道整体的安全系数Fs是偏安全的也是合理的。

4.2 有限差分法验证

目前，采用FLAC有限差分软件结合强度折减法被广泛应用于研究边坡和隧道的稳定性问题，本文将采用此方法计算隧道的安全系数，采用Mohr-Coulomb本构模型，计算参数见表1，隧道埋深为25 m，开挖高度为14 m，开挖跨度为11.7 m，θ=108°40′18″，为方便本文方法与有限差分法进行对比，暂不考虑支护力的作用，本文方法的安全系数计算值和有限差分法计算值随黏聚力、内摩擦角的变化规律见图4。

表1 物理力学计算参数

图4 本文方法与有限差分法对比

由图4可知，本文方法的安全系数计算值和有限差分法计算值随黏聚力、内摩擦角的变化规律基本一致，均随着黏聚力、内摩擦角的增大而增大，两种方法的计算值误差范围在-9.74%～-2.04%，可见本文方法是偏安全的也是在一定的精度范围内，而有限差分法没有考虑到黄土垂直节理发育对稳定性的影响，实际的安全系数必然比有限差分法计算值偏小，本文方法求解的安全系数相对于文献[5-6]的研究偏安全，但考虑到黄土垂直节理发育降低围岩的稳定性，本文方法求解的安全系数显然是合理的。

5 安全系数和破裂面范围的参数影分析

5.1 安全系数的参数影响分析

为明确不同参数对浅埋黄土隧道安全系数Fs的影响规律，本文分析单一变量下安全系数的变化规律。令围岩内摩擦角φ=0～60°，重度γ=17～23 kN/m3，隧道埋深h=5～40 m，开挖高度H=13.38 m，跨度B=15.4 m，黏聚力c=0～70 kPa，侧压力系数λ=1.2，孔隙水压力系数ru=0～0.9，地面荷载σs=0～120 kPa，支护力q=100～260 kPa。当支护力q=250 kPa时，孔隙水压力作用下安全系数Fs的变化规律见图5。当σs=0 kPa时，孔隙水压力作用下不同参数变化下安全系数Fs的变化规律见图6。

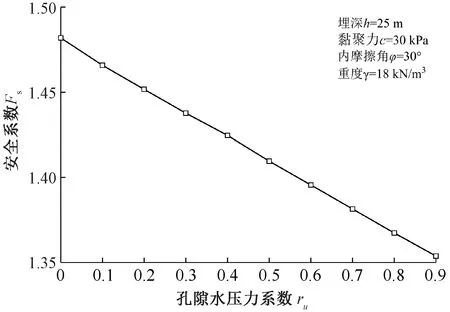
图5 孔隙水压力对安全系数的影响规律

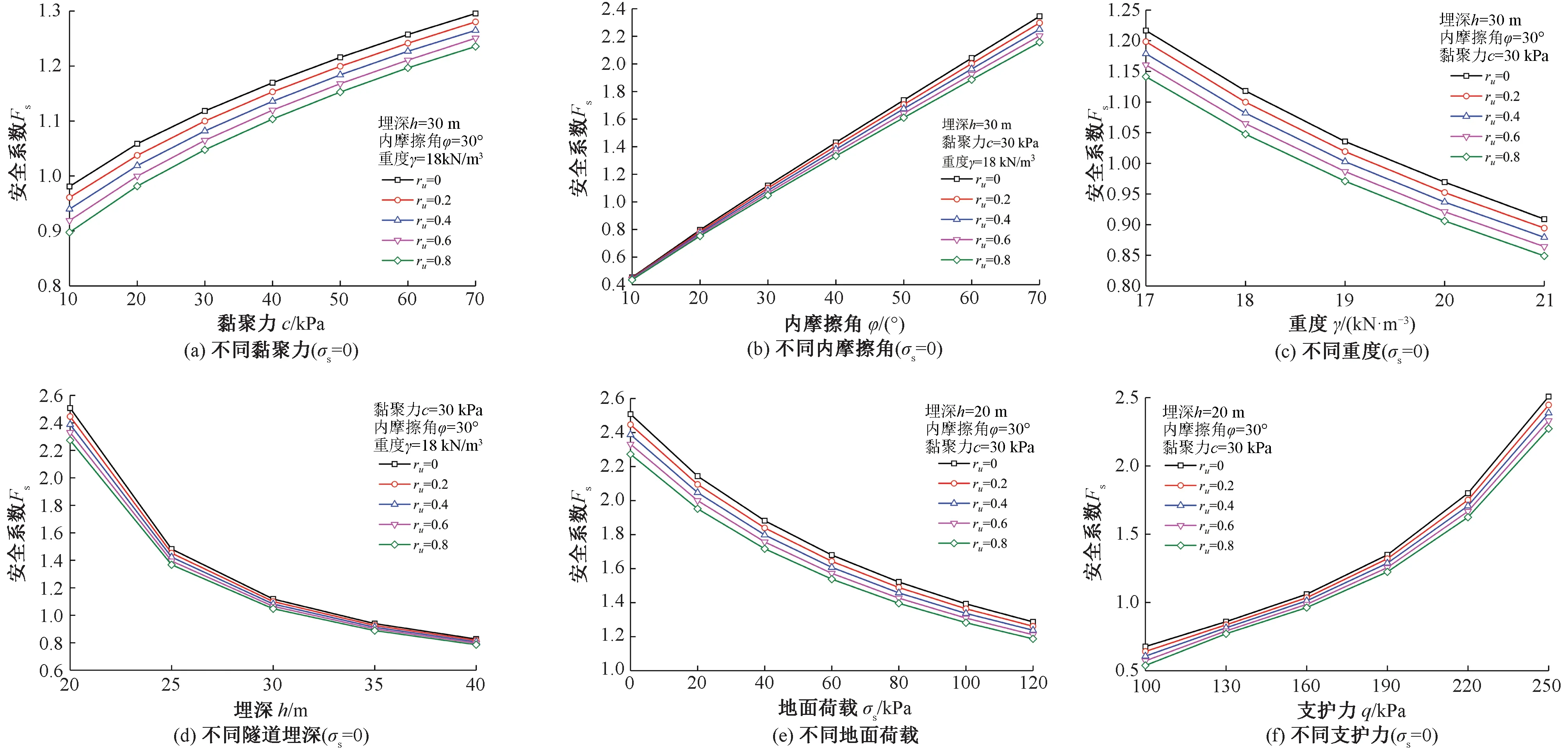
图6 安全系数随参数的变化关系

由图5可知，孔隙水压力系数ru=0即不考虑孔隙水压力的作用时，浅埋黄土隧道的安全系数Fs最大，而随着孔隙水压力系数的增大安全系数Fs不断减小，即孔隙水压力增大将降低浅埋黄土隧道的稳定性，可见孔隙水压力对浅埋黄土隧道的稳定性影响显著。

由图6可知，不同孔隙水压力作用下，浅埋黄土隧道的安全系数Fs随参数变化的规律基本上是一致的。浅埋黄土隧道的安全系数Fs随黏聚力、内摩擦角和支护力的增大而增大，黏聚力、内摩擦角的增大使土体的抗剪强度变大从而提高土体的稳定性；不同孔隙水压力作用下安全系数Fs随黏聚力和支护力的增幅基本是一致的；孔隙水压力系数越大，安全系数Fs随内摩擦角的增幅越小。浅埋黄土隧道的安全系数Fs随重度、地面荷载和隧道埋深的增大而减小，不同孔隙水压力系数下安全系数Fs随重度和地面荷载的降幅是一样的；孔隙水压力系数越大，安全系数Fs随重度的降幅越小。在实际工程中应该充分考虑孔隙水压力、土体的物理力学参数及重度、隧道埋深、支护力的变化对浅埋黄土隧道稳定性的影响，从而控制实际工程的风险。

5.2 破裂面范围的参数影响分析

为确定参数变化对浅埋黄土隧道破裂面范围的影响，参数取值同5.1节，块体数量取n=25，则边界DiDi+1的长度可以近似看成一段圆弧，将所有边界DiDi+1连接起来做光滑处理，参数对破裂面范围的影响规律见图7。

由图7可知，土体参数黏聚力c及重度γ对浅埋黄土隧道破裂面的范围影响不明显，破裂面的范围随着黏聚力c的增大而缓慢减小，随着内摩擦角φ的增大而减小，黏聚力和内摩擦角的增大也使土体的抗剪强度变大，从而提高浅埋黄土隧道的稳定性；破裂面范围随着重度γ的增大而缓慢增大，孔隙水压力对破裂面的范围影响亦不大，破裂面的范围随着孔隙水压力系数ru的增大而缓慢增大。破裂面的范围随着埋深的增大而增大，隧道埋深对浅埋黄土隧道破裂面的范围影响显著。

合理确定浅埋黄土隧道开挖引起的破裂面的范围，对其进行加固有利于提高隧道开挖过程中的稳定性，也可对隧道上方建筑环境的影响进行合理的评价。

6 结 论

本文结合现场浅埋黄土隧道的坍塌形式，构建二维刚性有限多块体平动破坏模式，基于极限分析上限法和序列二次优化并考虑孔隙水压力的作用，求解浅埋黄土隧道的安全系数和破裂面的范围，分析不同参数对隧道安全系数和破裂面范围的影响，主要研究结论如下：

(1)既有研究成果不能满足浅埋黄土隧道的实际需要，通过将本文方法的安全系数计算值和文献[9]计算值、有限差分法计算值进行了对比，验证了本文方法的合理性。

(2)参数的变化对安全系数的影响明显，浅埋黄土隧道的安全系数随着黏聚力、内摩擦角和支护力的增大而增大，随着重度、隧道埋深和地面荷载的增大而减小；孔隙水压力对浅埋黄土隧道的稳定性影响也比较明显，安全系数计算值随着孔隙水压力系数的增大呈线性的减小，不同孔隙水压力系数下安全系数随参数变化的规律基本一致。

(3)浅埋黄土隧道开挖引起的破裂面的范围随着参数的变化而变化，但土体的黏聚力、重度和孔隙水压力系数对破裂面的范围影响比较小，破裂面的范围随着黏聚力和内摩擦角的增大而减小，随着重度和孔隙水压力系数的增大而增大；而隧道埋深对破裂面范围的影响最为明显，破裂面范围随着埋深的增大而增大。

既有研究方法难以满足浅埋黄土隧道工程的实际需要，本文方法分析浅埋黄土隧道的稳定性具有重要的参考价值，是计算浅埋黄土隧道安全系数和破裂面范围可靠的方法。