基于传递矩阵法的轨道结构动力分析方法

2022-01-07朱志辉王盈莹蒋丽忠

铁道学报 2021年11期

朱志辉，王盈莹，龚威，张磊，蒋丽忠

(1.中南大学土木工程学院，湖南长沙 410075；2.中南大学高速铁路建造技术国家工程实验室，湖南长沙 410075)

轨道结构作为铁路系统中最重要的结构之一，具有引导列车运行方向与传递列车荷载至下部结构的作用[1]。作为列车的直接支撑结构，轨道结构振动响应直接影响轮轨相互作用力、列车行车安全性与乘坐舒适度的评估[2]。因此考虑轨道结构的柔性支撑作用，建立准确的轨道结构动力学模型一直是列车-轨道-桥梁耦合动力学理论研究重要部分。

由于轨道结构中存在局部与高频振动[3-4]，为避免模态叠加法在有效振型选择上的困难，部分学者基于精细有限元模型，采用有限元直接刚度法(Direct Stiffness Method，DSM)建立其动力方程[5-6]。这种方法虽然可以准确计算轨道结构的局部与高频振动[7]，但涉及超长轨道结构动力分析时，DSM不可避免会产生大量结构自由度，使得动力方程系数矩阵规模庞大，导致计算困难[8]。针对该问题，移动轨道技术[9-10]被用于降低轨道结构自由度数目，该方法通过保留荷载作用处与附近一段长度范围内的轨道结构，删除其余非荷载作用处轨道结构以达到降低自由度数目的目的。但该方法在引入新增轨道结构时，由于新增轨道和原有轨道结构在连接处存在位移不协调问题，从而导致新增单元处动力响应突变的问题[11]。

由于轨道结构具有明显的周期特征，很多学者针对其频域动力分析提出了周期Floquet变换法[12]、周期Fourier模态法[13]等求解方法，有效解决了轨道结构频响分析问题。但该类频域方法无法考虑轨道构成的差异性及非线性特征。因此，本文利用传递矩阵方法[14]，建立周期性轨道结构模型，并在时域范围内求解其动力响应，以更好地解决前述问题。

传递矩阵法(Transfer Matrix Method，TMM)的基本思想是针对周期性结构，通过将其重复性部分划分为若干元胞，建立元胞内部及相邻元胞间的状态矢量传递关系，实现整个周期性结构的求解。因此TMM并不适用于非周期性结构，但对于周期性结构，由于TMM无需建立结构的整体动力方程，避免了大型线性方程组的求解[15]；同时，由于元胞本身自由度非常小，因此该方法可有效减少结构的自由度数目，降低计算过程中的内存占用，并使得模型的建立更为便捷[16]，能较好地解决由于轨道结构自由度数目过多导致的计算困难和计算效率低下的问题。文献[17-20]采用该方法，分别针对周期性的弹性支承梁、桁架结构、框架结构和圆柱壳体进行了研究，取得了良好的效果。

上述研究中，系统传递关系通过传递矩阵的连乘方式建立，广泛用于结构静力及动力特性问题的分析求解。但对于结构瞬态动力分析，由于传递矩阵中考虑了等效刚度和等效荷载，且相较于刚度矩阵和荷载向量二者元素更大，因此连乘算法中的累积误差被加剧，导致时域数值积分过程中存在计算不稳定现象[21]。针对该问题，Horner等[22]提出了适用于链式结构的Riccati传递矩阵法，通过传递矩阵的递推建立系统传递关系，有效提高了TMM的数值稳定性。Xue[14]在相邻元胞交界处引入了刚度方程假定，克服了上述方法元胞边界自由度相等的限制，将其扩展至一般结构。上述关于周期性结构的研究，很好地推动了TMM的推广应用，但其在轨道结构中多用于波传播特性分析[23]，涉及时域分析的研究还较少。

本文针对具有显著周期性特征、且通常需要考虑较长长度的轨道结构，将轨道结构的周期性重复部分划分为若干类元胞结构，基于链式结构的Riccati传递矩阵法，确定元胞内部及相邻元胞间的传递关系，从而建立周期性轨道结构传递矩阵模型。以有砟轨道和CRTSⅡ型板式无砟轨道为例，基于本文方法分别提出了对应的轨道结构元胞划分方案，通过TMM计算所得移动荷载引起的有砟轨道结构动力响应结果，对比文献数据验证了本文方法的准确性。以移动荷载列通过无砟轨道结构为例，对比TMM和DSM计算结果验证了本文方法的高效性。

1 时域传递矩阵法

1.1 元胞单元时域传递关系

以周期支承的平面梁为例，采用传递矩阵法时，可将其划分为A、B、C三类元胞结构，其中，第1个元胞为A类，第2～n-1个元胞为B类，第n个元胞为C类。对于元胞B，由于相邻两元胞包含同一支承结构，其支承刚度为原始刚度的1/2；对于元胞A，由于其处于整个结构的输入端，故元胞输入端支承刚度保持不变，输出端支承刚度为原始刚度的1/2；同理，元胞C输入端支承刚度为原始刚度的1/2，输出端支承刚度与原始取值相同，见图1。

图1 周期性结构的元胞结构划分示意

任意取其中第i个元胞，则t+Δt时刻其运动方程为

(1)

采用Newmark-β法对上述方程进行求解，则有

(2)

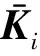
图2 元胞i输入端I与输出端O向量传递关系示意

则对于元胞i有

(3)

将其代入式(2)可得

(4)

(5)

展开式(5)，则有

(6)

(7)

考虑位移和内力的连续性[25]，则剖面两侧的位移相等，内力相反，故相邻两元胞间状态矢量的传递关系可表示为

Ui,I=Ui-1,ONi,I=-Ni-1,O

(8)

类似状态矢量的广义Riccita变换[22]，假设联系元胞i输入端内力与位移向量的广义刚度方程为

Ni,I=SiUi,I+Eii>2

(9)

式中：Si和Ei分别为第i个剖面的刚度方程系数矩阵和等效外荷载向量。

将式(8)和式(9)代入式(6)，可得元胞i+1输入端内力与位移向量的广义刚度方程为

(10)

将式(10)代入式(7)，可得元胞i+1输入端内力与位移向量的广义刚度方程为

Ni+1,I=Si+1Ui+1,I+Ei+1

(11)

(12)

(13)

式(12)和式(13)即为相邻剖面间，刚度方程系数矩阵和等效外荷载向量的传递关系。

若S2和E2已知，则通过上述两式可依次解得各剖面的Si和Ei，进而建立整体结构的状态矢量传递模型(以下简称为“传递模型”)。结合式(9)可知，第n+1个剖面处(结构输出端)内力与位移的广义刚度方程可表示为

Nn+1,I=Sn+1Un+1,I+En+1

(14)

式中：n为系统元胞个数。

考虑结构输出端边界条件，通过式(14)可得该处位移响应。将式(14)代入式(10)，由输出端至输入端依次求解，可得各元胞的位移响应，并通过Newmark-β方法解得其速度和加速度响应。

1.2 传递系数求解

式(11)中，令i=1，可得

N2,I=S2U2,I+E2

(15)

将式(8)代入式(15)可得

N1,O=-S2U1,O-E2

(16)

对于元胞1，扩展式(5)可得

(17)

(18)

考虑结构输入端边界条件，结合式(17)、式(18)，可解得U1,O和N1,O间的关系，进而对照式(15)可解得对应边界条件下的S2和E2。

对于位移边界条件，U1,I是已知的，因此由式(18)可得元胞1的输出端内力为

(19)

对照式(16)可知

(20)

(21)

对于荷载边界条件，N1,I是已知的，因此由式(17)可得元胞1的输入端位移为

(22)

将式(22)代入式(18)，可得元胞1的输出端内力为

(23)

对照式(16)可知

(24)

(25)

(26)

类似地，展开式(26)，求解N1,O和U1,O间的关系，对照式(16)可得

(27)

(28)

1.3 计算流程

根据上述理论，基于Matlab平台编制了外荷载作用下的周期结构瞬态响应的TMM求解程序，主要计算流程见图3。

图3 传递矩阵法计算流程

2 轨道结构的传递矩阵模型

目前，我国铁路中铺设有多种类型的轨道结构，其结构形式和力学特征均有所不同。本节分别针对有砟轨道和CRTSⅡ型板式无砟轨道，提出了对应的元胞划分方案，并基于TMM方法建立了元胞间的动力传递关系。为简便起见，采用垂向轨道模型对方法进行介绍，只考虑轨道结构在竖向平面内的动力响应。

2.1 有砟轨道元胞模型及传递关系

有砟轨道由钢轨、扣件、轨枕和道砟组成，其垂向整体模型见图4(a)，单跨模型(相邻两轨枕间轨道结构)及其节点自由度如图4(b)。其中，钢轨视作连续弹性离散点支撑的垂向Timoshenko梁模型，考虑竖向位移Zr及转动角θr，长度为L；轨枕(及道砟质量)等效为集中质量ms[30]，考虑竖向位移Zs，相邻两轨枕间距为l；扣件支撑和道砟支撑等效为弹簧-阻尼器，考虑竖向刚度系数kf、kb及阻尼系数cf、cb。

图4 有砟轨道垂向模型示意

有砟轨道以轨枕间距l为周期，其构成具有重复性，因此应用传递矩阵法时，仅需对单跨轨道进行划分。为对钢轨进行较为精细的划分，如图5所示，将单跨轨道划分为3类元胞结构：元胞A为左侧支撑结构，由长度为l1的钢轨、轨枕、扣件和道砟组成；元胞B为中间连接结构，由长度为l2的钢轨组成；元胞C为右侧支撑结构，除钢轨长度为l3外，其余构成与元胞A相同，且二者参数均为整体轨道结构的1/2(轨道输入及输出端处理方式与1.1节相同，由于整个系统仅包含2个端部元胞，数量极少，不再单独列出，下同)。由图可知，元胞A、B和C的输入/输出端节点自由度数目分别为3/2、2/2、2/3。

图5 有砟轨道结构划分示意

根据相邻元胞结构间的传递关系，进而建立整体轨道结构的传递模型。有砟轨道传递模型中存在A↔B、B↔B、B↔C和C↔A共4种传递关系，其中，求解传递系数时方向由输入端至输出端(A→B，B→B，B→C，C→A)，求解响应时方向由输出端至输入端(A→C，C→B，B→B，B→A)。以A↔B为例，假设第i和i+1个元胞的类型分别为A和B，则有

(29)

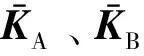
对于由梁、质量块、线性弹簧阻尼器等简单构件组成的元胞结构，可利用有限元理论直接推导其系数矩阵[15]，对于由薄板、实体等复杂构件组成的元胞结构，可在通用软件(如Ansys)中建立有限元模型，导出其系数矩阵[26]。

元胞i输入和输出端位移和内力可表示为

(30)

式中：Z和θ分别为位移和转角；Q和M分别为剪力和弯矩；下标r和s分别为钢轨和轨枕。

将式(29)、式(30)代入式(5)，可得元胞i的动力方程为

(31)

将式(31)代入式(12)和式(13)，可实现建模过程中元胞i→i+1(A→B)等效刚度及荷载的传递，即

(32)

(33)

轨道结构两端无内力作用，适用于荷载边界条件，式(32)和式(33)中Si和Ei可在由式(24)和式(25)解得传递系数S2和E2后，循环应用式(12)和式(13)计算得到。

将式(32)和式(33)代入式(10)，可得求解过程中元胞i+1→i(B→A)位移响应的传递，即

(34)

各元胞位移响应可在由式(14)解得边界处的响应后，循环应用式(34)计算得到。至此，已完成元胞A↔B传递关系的建立，其他3种传递关系也可通过上述方式导得。结合轨道结构中各类元胞结构的排列顺序，应用对应的传递关系，可实现相邻元胞间状态矢量的传递，从而完成有砟轨道的建模和求解。

由上述推导过程可知，采用传递矩阵法对有砟轨道结构进行动力分析时，无需建立其整体模型。仅需对重复构成的单跨轨道进行拆分，并依据各类元胞结构间的传递关系和其在整体结构中的排列顺序，建立整体轨道结构的传递模型即可。对于垂向有砟轨道模型，无论轨道长度L如何变化，计算过程中所涉及的最大矩阵阶数始终为3。

2.2 无砟轨道元胞模型及传递关系

与传统的有砟轨道相比，无砟轨道具有结构稳定性高、刚度均匀性好等突出优点[27-28]。CRTSⅡ型板式无砟轨道是我国广泛应用的无砟轨道结构形式之一，京津城际、京沪高铁等均采用了此种轨道结构[29]。本文以CRTSⅡ型纵连板式无砟轨道垂向模型为例，介绍基于传递矩阵法的无砟轨道动力分析方法。

CRTSⅡ型板式无砟轨道垂向模型由钢轨、扣件、预制混凝土轨道板、水泥乳化沥青调整层(CA砂浆)和混凝土底座板等部分组成，见图6(a)。其中，钢轨、轨道板和底座板视作连续弹性离散点支撑的Timoshenko梁模型，长度为Lr，考虑竖向位移Zr、Zt、Zc及转动角θr、θt、θc；扣件、CA砂浆和基础以离散分布的黏滞阻尼和线性弹簧表示，间距为l，考虑竖向刚度系数kf、kc、kb和阻尼系数cf、cc、cb，见图6(b)。

图6 CRTSⅡ型板式无砟轨道垂向模型示意

CRTSⅡ型板式无砟轨道可认为由图6(b)所示的单跨轨道重复构成，因此，应用传递矩阵法时，仅需要对单跨轨道进行划分。如图7所示，类似有砟轨道，将其划分为A、B和C三类元胞结构。其中，元胞A和C均由钢轨、轨道板、底座板、扣件、CA砂浆和地基组成，长度分别为l1和l2，连接件参数取值相同，均为整体模型的1/2；元胞B由钢轨、轨道板和底座板组成，长度为l3。由图6可知，元胞A、B和C的输入/出端的节点自由度数目均为6/6。

图7 CRTSⅡ型板式无砟轨道划分示意

类似式(34)，元胞i和i+1间位移响应的传递关系可表示为

(35)

由上述推导过程可知，采用传递矩阵法对无砟轨道进行动力分析时，同样无需建立整体模型。仅需对单跨轨道进行划分，并对各类元胞结构进行计算即可。对于垂向无砟轨道模型，无论轨道长度L如何变化，计算过程中所涉及的最大矩阵阶数始终为6。

3 移动荷载作用下轨道结构动力响应分析

为验证上述关于轨道结构传递矩阵算法的正确性，本节以移动荷载作用下的有砟轨道结构为例，对比了TMM、DSM和文献中的钢轨动力响应计算结果。并以自由度数目较多的空间无砟轨道结构为例，对比了TMM和DSM计算所得的移动荷载作用下轨道结构动力响应结果，进一步验证了本文方法的高效性。

3.1 有砟轨道动力响应分析

文献[30]给出了移动荷载F=1 kN以速度60 km/h移动时的跨中(坐标x=60.3 m)钢轨位移时程曲线，本文通过TMM和DSM计算相同的算例，将得出的结果与文献结果进行对照，以验本文方法的正确性。

TMM和DSM计算的钢轨跨中竖向位移的结果和文献中的钢轨竖向位移结果见图8。由图8可知，两种方法计算所得钢轨位移时程曲线几乎完全一致，且与文献[30]的结果在幅值和趋势上吻合良好，表明本文方法具有较高的计算精度，以及其用于轨道结构的动力分析是可行的。

图8 有砟轨道跨中钢轨竖向位移

3.2 无砟轨道动力响应分析

为进一步对比TMM和DSM的计算效率，本节以移动荷载作用下的空间无砟轨道为例，通过不同方法计算耗时的对比，对TMM的计算效率进行说明。

CRTSⅡ型板式无砟轨道长度为30 m，扣件纵向间距为0.6 m，轨道板长6 m。对于空间的无砟轨道，其元胞划分方案与平面无砟轨道结构类似，元胞A、B、C的长度均为0.1 m。相对于平面轨道结构，空间无砟轨道的构成较为复杂，其组成构件中包含轨道板和底座板，因此难以通过理论方式准确地描述其动力特性。本文采用有限元法建立元胞结构的模型，并从中导出其质量、刚度和阻尼矩阵进行计算。无砟轨道结构详细参数见表1。