三维元胞自动机模拟微生物生长研究
2022-04-11薄兴野谢瑞洁王艳东张如意刘振宇
薄兴野,谢瑞洁,陈 敏,王艳东,张如意,刘振宇
(1.山西农业大学信息科学与工程学院,山西 晋中 030801;2.山西农业大学农业工程学院,山西 晋中 030801)
0 引言
微生物个体相对简单,但其整个生长过程表现出复杂的行为且数量庞大,同时微生物生长和繁殖表现出种群效应[1-2]。当前,描述微生物生长通常使用生长动力学方程,通常为非线性数学模型,是一类确定性的机理模型[3-4]。这类模型不能表现出微生物生长过程中存在的多样性、随机性与不确定性,以及对初始状态的敏感性。元胞自动机是解决这些问题的有效工具。
元胞自动机是由无限个元胞组成的世界,所有元胞都处于某种状态并具有相似的形状,在每次演化过程中,每个元胞按照相同规则,根据本身状态和邻域状态改变状态。赵峰等[5]使用二维元胞自动机模拟了菌落生长的分形结构。李向阳[6]使用莫诺德方程推导的差分方程模拟了微生物细胞的生长。PICIOREANU C等[7]通过使用二维元胞自动机与三维元胞自动机模拟生物膜在凝胶珠生长,说明三维元胞自动机能更好模拟微生物生长。目前,由于三维元胞自动机设计复杂、运行优化难度大,研究者多用二维元胞自动机代替,其不能真实模拟微生物在生长中与环境的相互作用。三维元胞自动机的使用会将微生物生长过程中复杂机理、动态行为,以及演化的多样性、随机性、不确定性和非线性等特点表现出来。同时,建立三维元胞自动机模型为研究微生物生长中与环境、与个体之间存在的依赖、竞争、关联等复杂相互作用提供了新思路[8]。
本研究基于Gompertz方程建立的差分方程,使用三维元胞自动机模拟微生物生长过程,根据设计规则编写Python程序,并进行仿真试验。仿真试验结果表明,三维元胞自动机能较好地描述微生物生长过程,并将生长过程可视化表现,对使用三维元胞自动机模拟微生物生长进行了新探索。
1 元胞自动机模型构建
采用接近微生物生长的三维概率性元胞自动机,每个元胞代表微生物存在所需三维空间,定义了微生物生长过程中相关的状态。元胞自动机通过制定合理规则,使各个元胞在不同状态值中不断转化,模拟微生物在一段时间内的生长。元胞自动机微生物生长模型的5个元祖,有
CA={Cell,State,Space,Neighborhood,Rules}
(1)
式中Cell——元胞,是元胞自动机的基本元素
State——元胞状态集合
Cellspace——元胞空间,代表有限空间
Neighborhood——邻域,代表元胞规则作用的域
Rules——元胞规则,是元胞自动机的核心,规定元胞状态的演化
1.1 离散时间
元胞自动机要对微生物生长时间进行离散化,对于每一个离散时间
t=kT0
k={0,1,…,N}
式中T0——时间间隔,即元胞自动机每次演进所代表的真实时间
N——最大演进次数
1.2 元胞与元胞空间
假设元胞自动机的元胞是边长为L的微小正方体。随机选取一个的边长为1 000L的正方体空间中微生物的生长。根据换算可得元胞空间Space={Sijk|i,j,k∈{0,1,2,…,1 000}},元胞空间中的元胞总数为1 000×1 000×1 000。
1.3 元胞邻域
元胞邻域是元胞规则的定义域,模型选用三维Moore型邻域,定义如下
N={Vi=(Vix,Viy,Viz)||Vix-Vox|≤1,|Viy-Voy|≤1,|Viz-Voz|≤1,(Vix,Viy,Viz∈Z3)}
(2)
式中Vox,Voy,Voz——中心元胞坐标
Vix,Viy,Viz——邻居元胞的坐标值
每个元胞有多达26个相邻元胞,远超二维元胞自动机。
1.4 元胞状态
定义当前元胞Cell(x,y,z)在t时刻的状态为Statexyz(t),每个元胞只有两种状态,即Statexyz(t)=0表示在t时刻Cell(x,y,z)为空,Statexyz(t)=i表示在t时刻Cell(x,y,z)被微生物占据,i表示元胞中存在的微生物数量。模型通过各个元胞状态值不断转化模拟微生物在三维空间中的生长过程。
2 元胞自动机规则设计
元胞自动机的下一时刻状态与上一时刻的邻域元胞和当前元胞状态有关,元胞需要根据设计的元胞规则演化。
2.1 微生物游走规则
微生物存在一定程度的运动行为,这是因为微生物运动有助于增强趋化性介导的养分吸收[9]。为更好表现微生物在元胞空间中的运动,假设微生物在时间间隔T0中做b次布朗运动,模拟微生物在空间中的运动情况[10]。设计随机游走规则为
foriinRange(Sxyz>0)forjinrange(b)Sij(t+1)=Stateij-1,Sij_(t+1)=Stateij_+1
(3)
式中Sxyz——当前元胞状态,取值≥0,代表当前元胞中微生物数量
i——当前元胞正在进行布朗运动的微生物
j——布朗运动次数
Sij(t+1)——当前元胞第i个微生物第j次进行布朗运动前微生物所处元胞位置及其状态变化规则
Sij_(t+1)——当前元胞第i个微生物第j次布朗运动后微生物所处元胞位置及其状态变化规则
2.2 微生物分裂规则
微生物生长常用Gompertz方程表示,如下
L(t)=A+Ceap{-exp[-B(t-M)]}
(4)
式中L(t)——菌数对数值,log cfu/mL
A——菌数初始值,log cfu/mL
C——细菌最大生长量,log cfu/mL
M——细菌在生长率最大时所对应的时间,h
t——生长时间,h
B——M时刻生长率,log cfu/(mL·h)
推导出差分方程,即
x(t+T0)-x(t)=10L(t+T0)-10L(t)
(5)
其中x(t)即每毫升所含微生物数量,为元胞自动机的概率演化提供指导。设计规则如下
IfSxyz(t)=1,then
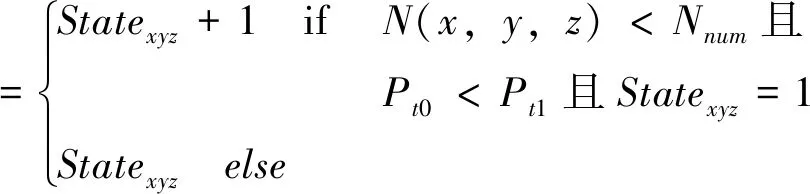
(6)
式中x、y、z——当前元胞坐标值
Statexyz(t+1)——元胞在t+1时刻状态
Statexyz——当前元胞在t时刻状态值
N(x,y,z)——t时刻元胞邻域中微生物的数量
Pt0——当前元胞在t时刻分裂的概率,为0~1随机数
Pt1——当前元胞在t时刻的概率阈值
概率阈值定义如下
Pt1=dx/(x(t)×(1-Pc))
(7)
式中dx——t至t+1时刻微生物的理论最大增长量
x(t)——t时刻理论生物量
假设当前元胞邻域中元胞状态非0数量为Nnum,则Pc为模型中每个元胞>Nnum或元胞状态>1时,元胞中的微生物数量与模型中当前时刻微生物数量之间的比值。
3 试验与仿真
3.1 试验材料和方法
(1)菌种:试验所用大肠杆菌由山西农业大学生命科学学院提供。
(2)药品:酵母提取物(山东玉宝生物科技有限公司);胰蛋白胨(武汉吉业升化工有限公司);氯化钠[西格玛奥德里奇(上海)贸易有限公司];琼脂(广州宏程生物科技有限公司)、蛋白胨(PEP,山东玉宝生物科技有限公司)。
(3)蛋白胨溶液:使用BS224S电子分析天平称取0.2 g蛋白胨放入300 mL三角锥形瓶中,用100 mL量筒经两次量取200 mL蒸馏水加入锥形瓶后,手持玻璃棒进行搅拌,直至观察到瓶中液体清澈,无固体粉末沉淀,再进行封口后放入高压灭菌锅灭菌,取出后放入双人单面净化工作台中备用。
(4)微生物检测:通过平板计数法对微生物进行检测。待检测的大肠杆菌稀释到适合浓度时,将其涂于培养基上,培养出细菌菌落后,计算生长出的细菌菌落数,得到单位体积细菌原始菌落数为计算出的菌落数乘以稀释倍数。为了计数准确,需要将待测细菌稀释浓度进行严格控制,确保平板上的细菌菌落数在30~300范围[11]。自然条件下在蛋白胨溶液中接种大肠杆菌培养12 h。
3.2 仿真结果
仿真试验利用Python语言,按照设计的结构编制元胞自动机程序,模拟以上试验中大肠杆菌在蛋白胨溶液中生长。演化程序包括以下功能。利用Gompertz方程计算出每一时刻的微生物数量,以及每次迭代的概率阈值,根据比例计算出在三维空间中微生物初始数量,并随机生成初始位置。在三维空间中,自动描绘微生物生长的状态图。计算每一时刻模型中微生物数量,并按比例计算出1 mL中的数量,描绘曲线图。
根据实际测得数据计算得出Gompertz方程的参数:A=7.32,C=2.585,B=0.417 76,M=2.096 9。设置时间间隔t=0.5 h,邻域中微生物阈值Nnum=15,布朗运动次数b=2。将值赋给程序,运行结果如图1所示。

图1 元胞自动机运行结果Fig.1 Cellular automata running results
其中图1a为元胞自动机初始转态,图1b为迭代24次的程序运行结果,可以看到微生物在经过布朗运动与分裂后,微生物有明显数量变化并向周围进行扩散,基本可以模拟微生物生长过程中的分裂与运动行为。
3.3 试验验证
微生物生长过程中活菌总数直接表现了微生物生长状态。图2中带点虚线为实际测出大肠杆菌菌数值(cfu/mL),虚线为根据Gompertz方程绘制出的曲线图,带点实线为元胞自动机模拟仿真大肠杆菌在蛋白胨溶液中菌数值(cfu/mL)。由图2可以初步看出,元胞自动机的设计与参数选择基本合理,可以与试验中实际大肠杆菌的生长菌数值吻合,并提供了三维可视化的参考。同时模型在初始时间与Gompertz方程基本相似,随着时间的进行模型活菌总数虽与Gompertz方程出现了较大的分离,但还是较为接近真实值。

图2 仿真过程中大肠杆菌总数随时间变化Fig.2 Total number of Escherichia coli changes over time during simulation
由于微生物数量庞大,通常会使用活菌对数值来表示微生物生长,大肠杆菌与元胞自动机仿真活菌数对数值如表1所示。以培养时间t(h)为横坐标,活菌数值log(cfu/mL)为纵坐标,大肠杆菌生长曲线拟合结果如图3所示。其中带点虚线为数据真实值表示,带点实线为仿真生长拟合曲线。
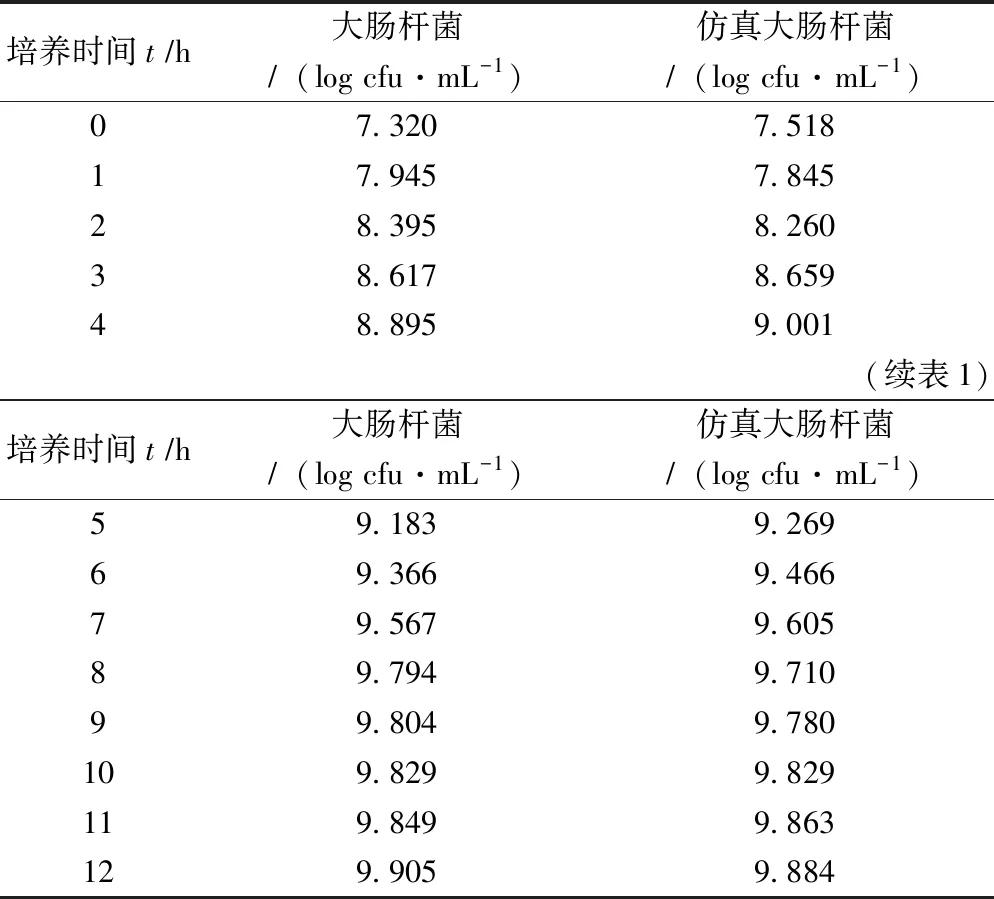
表1 大肠杆菌与元胞自动机仿真活菌数对数Tab.1 Logarithm of number of live bacteria simulated by Escherichia coli and cellular automata
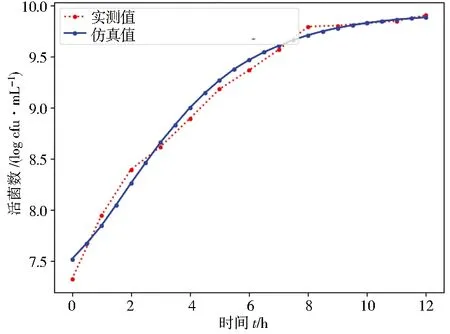
图3 大肠杆菌拟合结果Fig.3 Escherichia coli fitting results
进行拟合计算,其精度为R2=0.985 68。可见其拟合精度较高,元胞自动机对大肠杆菌的生长仿真较好。在培养时间为0时,数据差值相对较大,这是由于元胞自动机随机生成的初始状态导致,随着时间推移,仿真得到的大肠杆菌对数值接近真实值。
4 结论
基于微生物生长机理建立了模拟微生物生长的三维概率元胞自动机,并得到以下结论。
(1)采用布朗运动方法可有效地在元胞自动机中模拟微生物的运动特性,微生物的运动能力随离散时间t内的布朗运动次数增大而增强,通过合理设置运动次数能较好模拟实际微生物运动。
(2)使用Gompertz方程推导的差分方程制定合理元胞规则来模拟微生物的分裂,在各个离散时间内元胞自动机仿真得到的微生物数量与实验数据接近。
(3)本次仿真通过设置元胞自动机时间间隔为t=0.5 h,邻域中微生物阈值Nnum=15,布朗运动次数b=2,Gompertz方程参数A=7.32,C=2.585,B=0.417 76,M=2.096 9,模拟大肠杆菌在蛋白胨溶液生长,拟合精度较高,并表现了微生物在三维空间中的分布与微生物生长的随机性与不确定性。
本研究未考虑微生物死亡状态并假定生长过程中营养物质充分,研究接下来会将微生物死亡状态加入探讨,同时引入营养物质不均衡状况并建立基于基因表达的元胞规则。
