高速列车的有限时间容错跟踪控制
2022-01-07徐传芳
徐传芳
(大连交通大学 自动化与电气工程学院,辽宁 大连 116028)
列车自动驾驶(Automatic Train Operation,ATO)可提高列车的运营效率和控制品质,是未来高速铁路列车运行控制的发展趋势。高性能的ATO技术是实现高速列车运行自动控制的基本前提,是轨道交通领域探索的一个热点。ATO主要有两个控制目标:基于列车对安全准点、舒适节能等性能指标的要求,以及列车运行线路信息等,计算得到期望速度优化曲线;将期望速度优化曲线作为系统跟踪控制的对象,设计合适的控制策略实现列车对期望曲线的精确跟踪[1]。目前,对期望速度曲线优化的研究已经取得了丰硕的成果[2-4],随之设计合适的列车速度跟踪控制策略,并实现列车对期望曲线的精确跟踪就成为需要研究的关键问题。然而,已有控制策略研究[5-8]均假设列车在运行中执行器健康无故障。实际上,列车在运行时由于频繁且长时间执行牵引/制动控制任务,执行机构时常发生故障。此时,若仍基于原有未考虑执行器故障的控制策略,列车将难以维持对期望曲线的跟踪性能,甚至会引发系统不稳定,危及旅客的人身和财产安全。
容错控制可有效补偿故障对系统性能的影响,提高系统的可靠性和安全性,为解决故障情况下高速列车的精确速度跟踪控制问题提供了有效途径。文献[9-14]针对执行器故障下高速列车的容错跟踪控制做了大量研究,并取得了良好的跟踪控制性能。但是,值得注意的是,这些文献忽略了执行器输出受到实际物理约束可能会引发输出饱和受限问题。一旦发生执行器输出饱和,不可避免地会出现系统性能下降甚至不稳定[15]。文献[16]提出了同时考虑执行器故障与饱和受限的高速列车自适应容错跟踪控制策略;文献[17]进一步考虑模型参数的时变不确定性,基于变增益PID型滑模面设计了高速列车的自适应容错跟踪控制器。它们虽然实现了同时考虑执行器故障与饱和受限约束下的高速列车容错跟踪控制,但是最终实现的是对期望曲线的渐进跟踪,列车的速度跟踪误差和位移跟踪误差收敛到零的时间在理论上为无穷大。
随着列车运行速度和发车密度不断提高,渐进时间收敛的列车速度跟踪控制策略已经难以满足乘客对于快速性、准点性、节能性等性能指标的要求。因此,很有必要研究有限时间收敛的速度跟踪控制策略,然而目前相关的文献还非常少[18-19]。尽管文献[18-19]引入非奇异终端滑模控制技术,实现了列车跟踪误差的有限时间收敛,然而它们均以执行器健康无故障且不会发生输出饱和为前提。
基于以上分析,本文针对同时存在执行器故障与输出饱和受限约束的高速列车,并考虑模型参数未知时变、附加阻力干扰等因素影响,研究其速度跟踪控制问题;引入自适应控制技术在线估计模型参数标称值与集总不确定性的上界,基于非奇异终端滑模控制技术设计有限时间收敛的高速列车容错跟踪控制策略;最后对所提出的控制算法进行严格的理论证明和仿真验证。
1 高速列车动力学模型
列车单质点模型将整列列车抽象为一个质点,受力分析简单,能够实时、准确、快速地模拟列车运行,常被应用于列车的跟踪运行控制[20]。根据牛顿第二定律,单质点模型[16-17]可以描述为

(1)

(2)
式中:m为列车质量;v为列车速度;F为牵引过程的列车牵引力或制动过程的列车制动力;d为附加阻力,主要由坡道、隧道、曲线等线路情况引起的阻力构成,在列车实际运行过程中,d随线路条件变化,难以精确测量;f为基本阻力,常采用经典Davis方程来描述。
f=a0+a1v+a2v2
(3)
式中:a0、a1、a2为正实数,通常通过风洞试验和实际运行过程所积累的数据获知。
在列车不同的运行时刻,列车模型参数m、a0、a1、a2会随载客量、乘客所携带行李、运行环境,以及列车速度等的改变在一定范围内变化,很难精确测定。因此,很有必要在建立列车动力学模型时考虑这些参数的时变不确定性。此时结合式(3),式(2)可进一步表示为
(4)
式中:Δm、Δa0、Δa1、Δa2为参数m、a0、a1、a2的时变不确定性部分。
假设1:假设附加阻力d满足|d|≤ξ<∞,ξ>0且未知。
在执行器故障中,效率部分损失故障最为常见[21],此时执行器的实际输出可表示为
F′=kcF
(5)
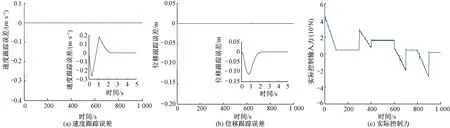
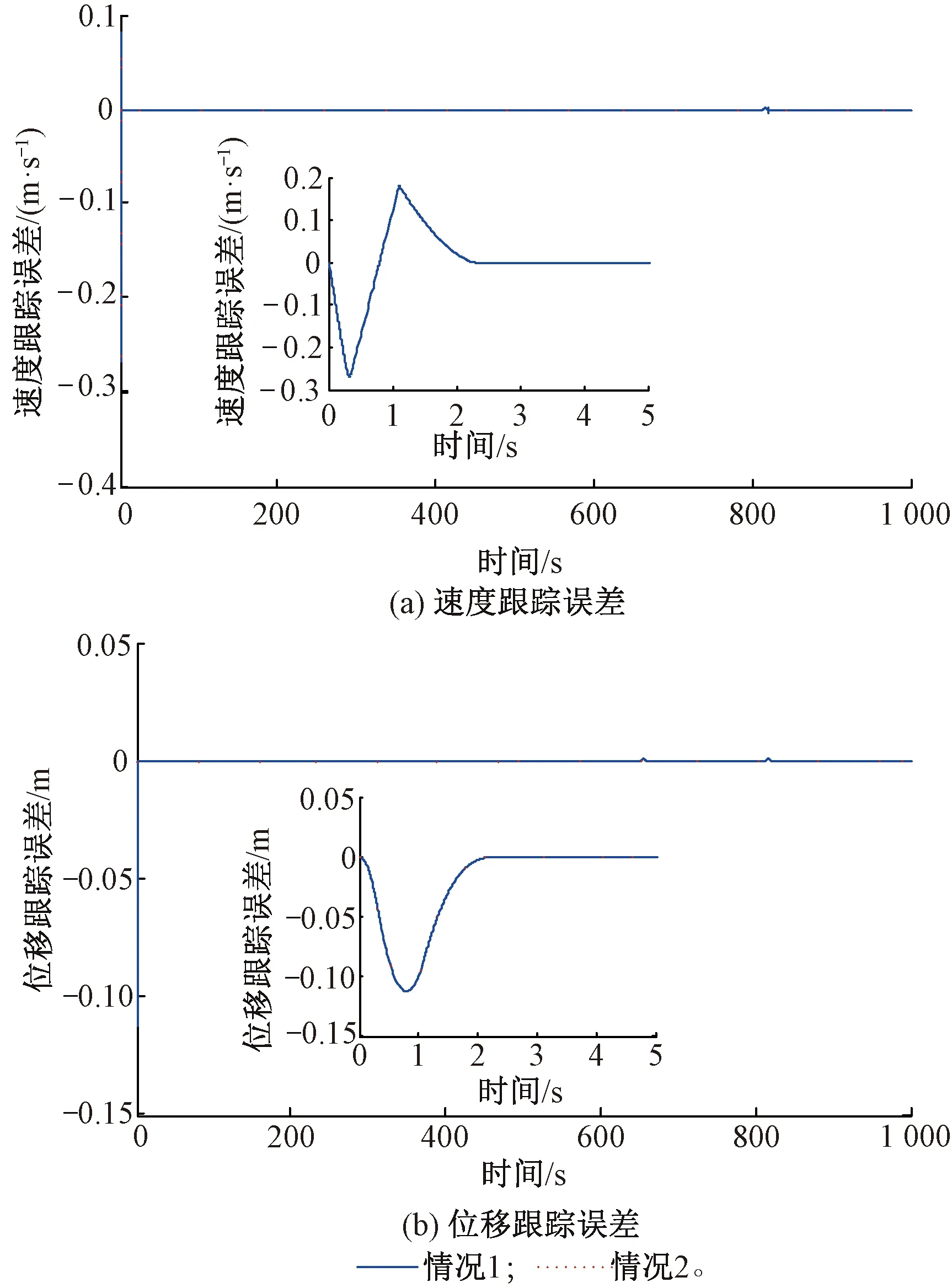
式中:F′为执行器实际输出;F为执行器健康无故障时的控制器输出;kc为执行器效率,满足0≤kc≤1,kc=0为执行器完全失效,kc=1为执行器完全健康,0 为了方便控制策略设计与稳定性分析,定义kc=1-τc,则式(5)变为 F′=(1-τc)F (6) 假设2:假设0≤τc<δ<1,且δ未知。 备注1:假设2说明执行器效率部分损失必须在一定限度内。若严重到一定程度,执行器所产生的牵引力/制动力不足以使得列车完成跟踪控制目标,则需要采取其他措施(比如修正期望速度优化曲线)。 在实际应用中,执行器输出不可避免地会受到诸如牵引电机最大输出等因素限制。为此,引入饱和函数sat(F)来表示考虑输出饱和约束限制时的执行器输出,其表达式为 (7) 式中:Fmax和Fmin分别为执行器输出的上界和下界。 定义σ(t)为执行器饱和输出与实际输出之间的差值,即 σ(t)=sat(F)-F (8) 在式(6)基础上进一步考虑输出饱和受限,则执行器的实际输出为 F′=(1-τc)sat(F)=(1-τc)[F+σ(t)] (9) 此时,式(4)可进一步表示为 (10) (11) 式中:θ=[a0a1a2];ζ(v)=[1vv2];P为系统的集总不确定性。 (12) 控制目标:基于自适应控制理论和非奇异终端滑模控制技术,针对受到执行器效率部分损失故障与输出饱和受限约束、模型参数未知时变以及附加阻力干扰等因素影响的高速列车,设计有限时间收敛的容错跟踪控制策略,实现高速列车对期望优化曲线的精确跟踪。 在控制器设计前,首先给出如下引理。 (13) 式中:V(x0)为V(x)的初值。 (14) 式中:β和γ为设计参数,β>0,1<γ<2;sign为符号函数。 s对时间求导,有 (15) 结合式(10)和式(15),可得到 (16) 基于自适应非奇异终端滑模控制技术,设计高速列车的有限时间收敛容错跟踪控制器为 F=F0+F1+F2+F3 (17) (18) (19) (20) F3=-τs-ksignq(s) (21) (22) (23) (24) (25) 式中:Γ1=diag(k0k1k2),Γ2=diag(l0l1l2),均为正定矩阵;k3>0;l3>0。 备注3:在所设计的控制器中,F0负责驱动系统状态沿滑模面到达稳定平衡点;F3负责迫使系统状态以非奇异终端滑模类型趋近律[23-24]到达滑模面;F1和F2则分别补偿系统集总不确定性和执行器故障对系统的影响。 证明:本文将从滑模运动的到达阶段和滑动模态阶段分两步来证明定理1的有限时间稳定性。 (1)到达阶段 选取Lyapunov函数 (26) 求V对时间的一阶导数 (27) 将式(16)和式(17)代入式(27),可得 (28) (29) (30) (31) (32) 将式(18)、式(22)、式(23)代入式(29),可以得到 (33) 结合式(12),并将式(19)和式(24)代入式(30),可得到Φ2满足如下关系: (34) 由式(20)和式(25),可得 (35) 将式(33)~式(35)代入式(28),并结合式(21)和式(32),以下不等式成立: (36) 由此可知,闭环系统在Lyapunov意义下稳定。 (37) (38) 式中:V(s0)为V的初始值;χ1和χ2分别为 (39) (40) (1-τc)[τs+k|s|q]< (1-τc)τs-(1-τc)k|s|q= P-T*ηT(v)+δ|F0|-δ|F0|- (1-τc)[τs+k|s|q]≤ -(1-τc)τs-(1-τc)k|s|q<0 (41) 如果s<0,则有 P+T*ηT(v)-δ|F0|+δ|F0|- (1-τc)[τs-k|s|q]≥ -(1-τc)τs+(1-τc)k|s|q>0 (42) (2)滑动阶段 参阅文献[26],分析如下: 当系统状态到达滑模面后,s=0,此时有 (43) (44) 结合式(44),对式(43)变形可得到 (45) (46) 综合以上分析可知,本文所设计的控制器可以实现高速列车跟踪误差在有限时间内收敛到零。定理1证毕。 备注4:列车跟踪误差的收敛时间取决于到达阶段和滑动阶段所需时间,其中:参数τ、k和q决定了到达阶段的收敛速度,τ、k越大,q越小,收敛速度越快,收敛时间越短;而参数β和γ在滑动模态阶段起重要作用,当0<β≤1且β和γ越小,或者当β>1且β越小,γ越大时,收敛速度越快。然而参数过大或过小都可能导致不可预料的抖振问题,因此应该在保证系统稳定的前提下权衡系统精度、收敛速度与抖振等折衷确定这些参数。 备注5:该控制器不依赖难以确定且时变的列车质量、基本阻力系数等模型参数以及附加阻力的具体信息。此外,虽然文中在处理执行器故障时引入了未知参数δ,但它仅在证明过程有所涉及,并没有出现在控制律和参数自适应更新律中,这使得本文所提出的控制器消除了对故障检测与诊断设备的依赖性,简化了控制器结构。 为了说明本文所提出控制策略的有效性,进行了仿真实验验证。仿真中的列车参数为[19]:m=500 t;g=9.8 m/s2;a0=5 880 N;a1=388 N·s·m-1;a2=8 N·s2·m-2;Δa0=200rand;Δa1=30rand;Δa2=0.2rand;Δm=1 000rand;rand为0到1之间的随机值。设置高速列车在不同运行时刻的附加阻力为[17] (47) 式中:we=0.000 131lemg/103,ws=10.5αsmg/(1 000ls),wr=mgsinθ,分别为线路情况为隧道、曲线和坡道时的附加阻力[28]。仿真中,隧道长度le=1 000 m,曲线长度ls=200 m,中心角αs=2π/3,坡度角θ=π/180°,其他阻力o(·)=1 500sin(0.02vt)。 表1 控制器、自适应更新律、滑模面参数 对包含2个加速、4个巡航、2个减速阶段的列车跟踪运行控制过程进行仿真,整个过程中列车最高运行速度为69.5 m/s(约250 km/h),运行时间为1 000 s,运行距离为47.5 km,所对应的期望曲线见图1。 图1 期望曲线 以下分4种情况进行仿真: (1)执行器未发生故障 执行器未发生故障情况下的仿真结果见图2。 图2 执行器未发生故障下的仿真结果 由图2可以看出,列车跟踪误差收敛速度很快,而且无论是稳态时还是工况切换时,列车对期望速度曲线和位移曲线均呈现出良好的跟踪性能。说明本文所提出的容错跟踪控制策略在执行器健康无故障情况下同样可行有效。 (2)执行器不同程度故障 对执行器不同程度故障下的系统性能进行仿真时,考虑执行器效率损失分别为10%、30%、50%,即kc=0.9、kc=0.7、kc=0.5三种情况。假设t=150 s时执行器发生故障并持续至仿真结束,其仿真结果见图3。 图3 执行器不同程度故障下的仿真结果 由图3可以看出,随着kc减小,执行器效率损失程度加重,故障对系统的影响越来越大。但是,从列车速度、位移的跟踪误差仿真结果可以看出,与无故障情况相比,高速列车的跟踪性能并未发生显著改变,当故障程度加重时,系统仍然能够保持对期望曲线的快速精确跟踪。同时,控制器的实际控制输入平滑,未出现明显抖振。由此表明,本文所提出的控制策略对执行器效率部分损失故障具备较强的补偿能力,体现出良好的容错跟踪性能。 (3)集总不确定性变大 集总不确定性增大时,分两种情况进行仿真。情况1:o(·)=2 500sin(0.02vt),θ=1.1π/180°,参数不确定性增加50%;情况2:o(·)=5 000sin(0.02vt),θ=1.2π/180°,参数不确定性增加100%。以kc=0.7为例,其速度跟踪误差与位移跟踪误差见图4。 由图4可以看出,系统集总不确定性增加并没有明显降低系统的控制性能,高速列车仍然保持较高的跟踪精度和较快的收敛速度。说明本文所提出的控制器对由参数时变、附加阻力等引起的系统集总不确定性具有强鲁棒性。 图4 集总不确定性变大时的仿真结果 (4)与其他仿真策略对比 为了验证本文所提出容错跟踪控制策略良好的收敛性能和跟踪性能,针对相同的执行器效率系数kc=0.7,与文献[17]提出的渐进时间收敛列车容错跟踪控制策略进行仿真对比。仿真结果见图5。其中,图5(a)和图5(b)为列车整个跟踪运行控制过程的跟踪误差,图5(c)和图5(d)为0~100 s之间的跟踪误差局部放大对比;图5(e)为滑模面响应曲线对比。 图5 本文结果与文献[17]仿真结果对比 由图5可以看出,跟文献[17]提出的基于变增益PID型滑模面的渐进时间收敛容错跟踪控制策略相比,本文所提出的控制策略稳态精度更高,收敛速度更快。 (1) 考虑执行器故障,输出饱和受限,列车质量、基本阻力系数等模型参数时变不确定及附加阻力干扰等因素的影响,融合自适应控制理论和非奇异终端滑模控制技术,提出了高速列车的容错跟踪控制策略,解决了多因素影响下列车自动驾驶中对期望曲线的跟踪控制问题。 (2) 所提出的控制器只需较少模型信息,实现了列车速度跟踪误差和位移跟踪误差的有限时间收敛。 (3) 仿真结果表明,该控制器对执行器效率部分损失故障具有较强的容错能力,对系统集总不确定性具有较强的鲁棒性,同时收敛速度快,跟踪精度高。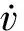

2 控制器设计及稳定性分析

2.1 控制器设计



2.2 有限时间稳定性分析


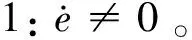









3 仿真验证及分析





4 结论
