小学数学巧用画线段图,提高解决问题的能力
2022-01-06马燕菲
马燕菲

摘要:数学教材中的图画是一种重要的学习资源,而数学教学中的画图是一种重要的学习策略,两者相辅相成、密不可分。作为教师,我们要鼓励学生多画图、会画图,善于利用画图来进行学习,利用画图来培养思维,利用画图来解决问题,这样就能使学生学得更加轻松,教学效果更好。鉴于此,本文对提高解决问题能力的小学数学画线段图教学策略进行了探索。
关键词:小学数学;画线段图;解决问题能力;提高策略
中图分类号:G4 文献标识码:A
一、画图分析能力培养的意义
1、符合小学生思考的特点
小学生在应用语言文字方面存在很大的劣势,其年龄小,对文字的认识较少,理解能力不足,对一些抽象的概念或者理论都不能很好地理解和接受,而在教学的过程中,教师一直用语言文字进行知识点的讲解,学生很容易就产生思想抛锚,不能理解,从而降低学习的兴趣,导致课堂效率下降。而画图的方式可以很好地帮助学生进行知识的学习,作为一种表达方式,画图可以很好地消除学生在学习数学知识过程中的枯燥乏味,让教学变得有趣起来,让学生的学习更主动积极。
运用画图分析更符合小学生的认知发展水平,能够帮助学生更加快速、有效地理解相关的知识,帮助学生更好地梳理题目中的条件和框架。运用画图分析,学生可以更容易理解数学概念,思考的路径更加清晰,从而更有效地探索出问题的答案。
2、画图分析有助于数学问题的解决
在数学教学过程中,画图是一种较为普遍的解决方法,运用广泛。画图可以帮助学生将一些比较抽象的问题或者理论直观形象地表现出来,让学生在画图的过程中更好地对题意进行梳理和理解,明白其中的数量关系,从而探索出解题的思路,提高学习效率。
数学中有很多题目仅靠单纯地阅读文字是很难理解的,所以这个时候就需要试着将文字叙述转化为图案,将抽象的题目用图案直观地表现出来,学生在构图的过程中可以对题目进行深入的思考,把握题目的基本结构,从而对问题有明确的认知。
画图分析的过程其实就是对数学问题的另一种重现,只是将问题中的数量关系单独提了出来,然后以画图的方式重新展示了出来,使数学问题更加简单易懂。
二、提高解决问题能力的小学数学画线段图教学策略
1、增强画图意识
(1)培养画图的兴趣
让一个人心无旁骛地投入学习中,最好的方法就是激发出他对学习的兴趣。学习过程是枯燥和无聊的,学生很容易就会产生无所谓甚至厌学的心理,所以,在教学的过程中,教师一定要注重学生的兴趣点,让学生学习的过程尽量变得有趣。小学生的学习经常随着心情变化,对感兴趣的事物可能会投入更多的时间进行学习并且保持很高的主动性,可以说兴趣就是小学生学习的最大动力,教师在教学的过程中培养学生对数学进行图形联想,可以有效地激发学生应用画图分析的方式解决问题的兴趣,能更好地培养学生画图分析的能力。
(2)理解画图的必要性
有些学生可能感觉画图的过程比较麻烦,因此在做题的过程中有能少画则少画的画图态度,当他们遇到一些特别难的题目时才会画图进行分析,希望通过这种方式找到解题的思路,学生总是很难意识到画图分析的作用。教师应该在教学过程中将画图的意识慢慢地传递给学生,让他们逐渐理解画图的重要性,理解遇到难题时画图的意义。
例如,一道关于两步计算的问题,有两个算式,算式一是28×3=84,84+28=112;算式二是1+3=4,4×28=112,运用这两种计算方法都可以得到正确的答案,但是许多学生对第一个式子很好理解,对第二个式子难以理解。教师此时就可以运用画图分析的方式引导学生进行算式的解析,以线段的方式进行画图,学生就可以直观地理解第二个式子中的加1是从哪来的,对计算方式豁然开朗,这样学生对画图的重要性和作用就能够更好地理解,懂得画图的意义和作用。
2、整合已知信息
当学生圈出了关键词之后,就可以通过画图形帮助理解题目意思了,标出已知量,并且将已知量用图形表示出来。与中、高年级不同的是一年级学生最喜欢用实物图或符号来表示题目中的数量关系,到了二、三年级,教师可以慢慢引导学生用线段图来表示,这样更简洁、方便。
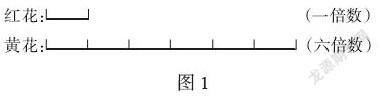
例如,“红花有8朵,黄花是红花的6倍,”已知量是“红花”,也就是红花是一倍数,而黄花是六倍数,教师可以根据题意引导学生自己画图,体会倍数关系,学生既可以用实物图,也可以用线段图表示如下(如图1):
学生通过画图,理清数量关系,已知一倍数求六倍数,用乘法算式解决。
同样的,如果题目已知:“黄花有21朵,黄花是红花的3倍,”己知量是“黄花”,也就是黄花是三倍数,红花是一倍数,学生画出如下线段图(如图2):
这时教师应该有意识的引导学生这道题目已知什么需要求什么?让学生进一步理解并不是所有的倍的解决问题都用乘法解决,相反这道题目已知三倍数求一倍数,用除法算式解决。
3、提升画图能力
有人说“学数学没有捷径可走,保证做题的数量和质量是学好数学的必由之路,但盲目的追求数量怎能保证质量呢?”所以,好的解题方法(数形结合)会让孩子们的学习事半功倍。
例如,“一个长方形的长是8厘米,宽是5厘米,如果把长减少了2厘米,这个长方形的周长减少了几厘米?”
没有画图学生列式是:
(8+5)×2=26厘米;(6+5)×2=22厘米;26-22=4厘米。
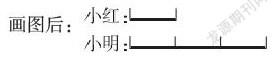
通過画图学生列式为:2×2=4厘米。画图后,这个长方形减少的周长清晰的展现在学生面前,学生就能直接列出算式了。又如:小红有12朵黄花,小明的黄花是小红的3倍,小明比小红多几朵?没有画图的学生列式是:12×3=36朵;36-12=24朵。
画图后:
通过画图学生列式为:2×12=24朵,当然,学生通过画图也能发现,原来图形能够帮助我们找到解决问题的关键,使得原来复杂的问题变得更简单,也正是通过图形检验,学生在问题的解决上找到了捷径。就像这道题目一样,学生做出来小明比小红多24朵,小红有12朵,说明小明有24+12=36朵,而36刚好是12的三倍,也就是线段图上画出来的小红一倍数,小明三倍数。
三、结语
掌握一个解题方法,比做一百道题更重要。实践证明,图形具有直观性、形象性、简洁性,如果学生从小掌握了用图形辅助解题的方法,分析问题和解决问题的能力将会大大的提高,对今后的数学学习将有很大的帮助。
参考文献
[1] 孙园园. 小学数学线段图的运用策略分析[J]. 数学学习与研究(教研版),2019(16):81.
[2] 廖君华. 线段图在小学数学”解决问题”教学中的应用探索[J]. 新课程·上旬,2019(1):97.
