混合润滑状态下板带轧机垂直振动特性研究
2022-01-04侯东晓时培明
侯东晓,徐 良,时培明
(1.东北大学秦皇岛分校 控制工程学院,河北 秦皇岛 066004; 2.燕山大学 电气工程学院,河北 秦皇岛 066004)
轧机振动问题一直是困扰钢铁行业的一个基础性难题,振动的频繁发生严重影响着产品质量和生产效率[1-3]。因此如何减少或抑制振动的发生,对稳定轧制生产有着重要的作用[4-5]。
针对长久存在的轧机振动问题,国内外专家学者对此进行了广泛的研究。刘浩然等[6]建立了轧件变形滞后非线性作用下辊系垂直振动动力学模型。Shi等[7]考虑轧机主传动系统接轴倾角和辊隙摩擦力的影响,建立了含参数激励刚度和非线性摩擦阻尼的主传动系统非线性振动模型。Amer等[8]采用多尺度摄动法求解了轧机的扭转振动系统,运用数值方法研究了系统的稳定性和稳态响应。范小彬等[9]考虑轧制界面非线性黏滑摩擦特性, 建立了轧辊水平方向摩擦颤振模型和工作辊水平方向“跳振”模型。孙建亮等[10]基于轧制理论和动力学理论建立了轧机水平振动与轧制过程参数的关系模型。Zeng等[11]建立了非线性摩擦下轧机垂直-水平-扭转耦合动力学模型,利用Hopf分岔代数准则对系统的稳定域进行了分析。Liu等[12]研究了轧机辊系水平-扭转耦合振动的静态和动态分岔特性,得到了系统的分岔和稳定性条件。
在轧制润滑方面,付括等[13]建立了稳态和非稳态轧制变形区油膜厚度分布模型,并应用卡尔曼方程分析其应力分布;Wang等[14]建立了不稳定润滑条件下的界面膜约束多重耦合模型,定量分析了一些参数对振动速度和振动位移的影响;Azushima等[15]提出了一种入口油膜厚度的估算方法;Noriki等[16]对轧件表面油膜和入口处乳化液的成膜机理的相互作用进行了研究。
本文考虑混合润滑摩擦的影响,建立了与入口油膜厚度有关的动态轧制力模型。考虑轧机辊系结构振动的影响,建立了轧机垂直非线性振动模型,并得到相应的动力学方程。通过数值仿真,分析了以轧制力参数和外扰力为变量的主共振幅频特性和分岔特性,为轧机振动问题的研究提供参考。
1 混合润滑摩擦状态下的非线性动态轧制力
1.1 动态轧制过程关键参数
考虑轧辊在垂直方向上的振动,建立了轧机辊系几何形状图,如图1所示。
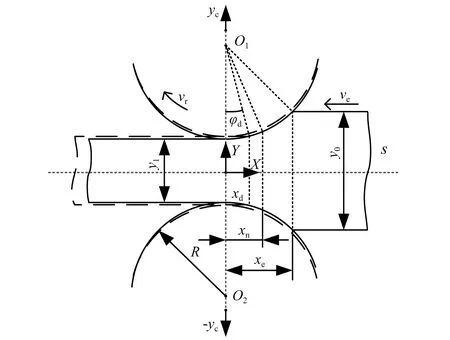
图1 轧机辊系几何形状
图1中:y0为带钢轧制前的厚度;y1为带钢轧制后的厚度;R为轧辊半径;l为变形区长度;s为后张力;ve为轧件的入口速度;vd为带钢的出口速度;vr为轧辊的轧制速度;xe为带钢的入口位置;xd为带钢的出口位置。
假设辊缝形状呈二次曲线分布[17],则变形区中任意位置的轧件厚度可以表示为
(1)
根据式(1)可以得到入口位置xe(yc)。
(2)
根据金属秒流量相等的原则,在考虑轧辊垂直振动时,金属秒流量公式应修正为
(3)
在变形区的中性点处,轧件的速度与轧辊的水平分速度相等。
(4)
当轧辊发生振动时,根据几何关系可得
(5)
联立式(1)和式(5),并代入式(3),得到方程
(6)
(7)
1.2 动态轧制力的计算
在轧件的变形区任意位置选取一微元体,如图2所示。
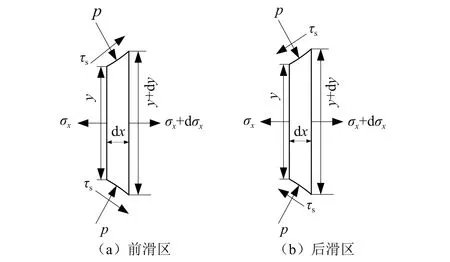
图2 变形区任意位置的应力关系示意图
根据力的平衡关系建立平衡方程。
(σx+dσx)(y(x)+dy(x))-σx·dy(x)+
2pdxtanφ∓2τsdx=0
(8)
式中:负号为从入口处到中性点处;正号为从中性点到出口处。根据几何关系可知tanφ=dy(x)/2dx,代入式(8),化简方程为
(9)
式中的屈服准则采用均匀变形下的von Mises屈服准则。
(10)
式中:σ为轧件材料的屈服强度;σx为正应力。
代入可得正应力的微分方程为
(11)
混合润滑摩擦状态下,轧件的摩擦切应力τs由干摩擦产生的摩擦切应力τa和全膜润滑产生的摩擦切应力τb按比例组成。
τs=λτa+(1-λ)τb
(12)
式中:τa为干摩擦产生的摩擦切应力,由黏着摩擦理论式(13)求得;τb为全膜润滑产生的摩擦切应力(由式(14)求得);λ为界面间的接触比。
(13)
(14)
式中:η0为乳化液的黏度;z变形区内润滑油膜的厚度,假设乳化液是不可压缩的,变形区内的润滑油膜厚度可由式(15)求得。
(15)
式中,z0为入口油膜厚度。在忽略表面形貌因素影响时,z0可由Wilson入口膜厚计算公式[18]求得。
(16)
式中:γ为乳化液的黏压系数;η0为标准大气压下乳化液的黏度。
将式(12)、式(13)、式(14)代入正应力微分方程式(11),并对式(11)进行积分可分别得到入口处、中性点处和出口处的应力。
(17)
(18)
(19)
将入口位置、中性点和出口位置的应力表达式分别代入式(10),可以分别得到入口位置、中性点和出口位置的压力pe,pn,pd。
假设轧制过程中轧件变形区的轧制压力近似线性分布[19],采用如图3所示的轧制力模型。根据代数关系式可以得到轧制力的表达式为
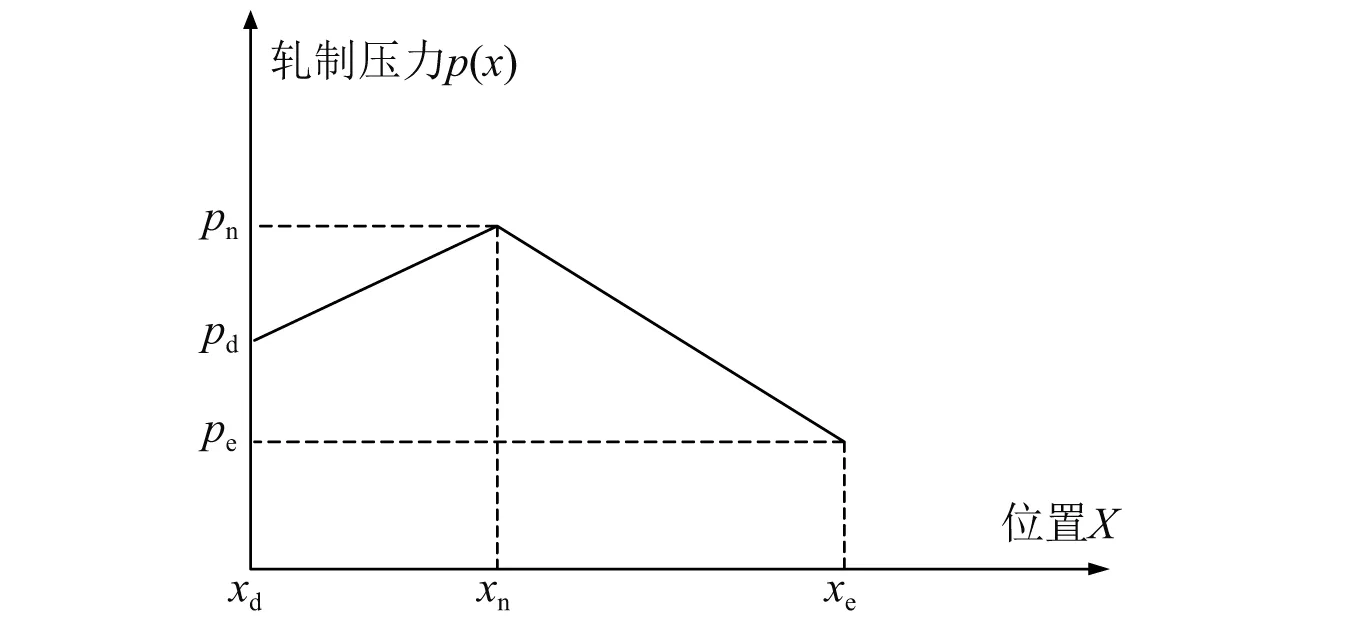
图3 变形区轧制压力分布示意图
(20)
将压力表达式和位置表达式代入其中并将轧制力进行Taylor展开,得到如下形式的动态轧制力。
F=F0+ΔF
(21)
式中:F0为稳态轧制力;ΔF为轧制力动态变化部分。
2 板带轧机垂直振动动力学模型
进一步考虑轧机机械结构影响,可建立了轧机辊系垂直振动模型,如图4所示。
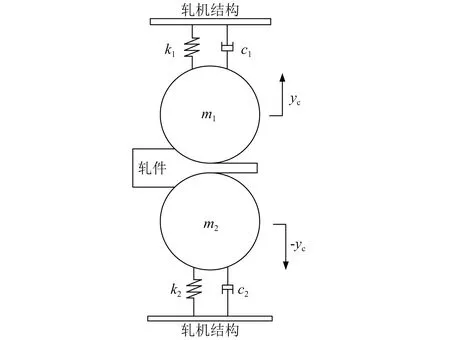
图4 轧机垂直振动模型
考虑到支撑辊质量远大于工作辊质量[20],可将其考虑为一个质量体,m1和m2分别为上下部辊系的等效质量;k1和c1为上辊系的等效刚度和等效阻尼;k2和c2为下辊系的等效刚度和阻尼;P1和P2分别为上下辊系受到的外扰力。
(22)
考虑到轧机机构具有对称性,有m1=m2,k1=k2,c1=c2,F1=F2,P1=P2,式(22)可以写成
(23)
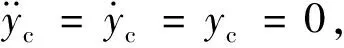
(24)
(25)
3 板带轧机垂直振动方程主共振响应求解
当轧机入口板带厚度或张力出现波动时,可导致周期性的外部扰动P=P0cos(Ωt)[21]。设式(25)是弱非线性系统,在式(25)右侧冠以小参数ε。
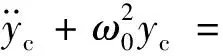
(26)
采用多尺度法对非线性系统求解,令Tn=εnt。
设式(26)的解为
yc(t)=y0(T0,T1)+εy1(T0,T1)
(27)
将式(27)代入式(26),令ε幂指数相同项相等,得
(28)

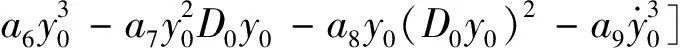
(29)
式中,Di=∂/∂Ti。
设式(28)的解为
(30)
主共振时外扰力频率Ω=ω0+εσ,将Ω表达式和式(30)代入式(29),消除方程的久期项,得
(31)
式中,σ为协调频率。
幅值A引入极坐标形式
(32)
将幅值的极坐标形式式(32)代入式(31),分离实部、虚部,并设ψ=σT1-φ1,得
(33)
(34)
4 仿真研究
采用某厂1780轧机参数进行仿真。轧机和轧件的参数:m=1.44×105kg,k=1.08×1011N/m,c=2.2×107N·s/m,y0=0.014 1 m,y1=0.008 2 m,R=0.42 m,s=3.6 MPa,σ=150.6 MPa;乳化液参数:γ=2×10-8Pa-1,η0=0.42 Pa·s,λ=0.8,z0=1.8×10-6m。动态轧制力的系数:a1=1.39×1010,a2=1.26×108,a3=4.81×1012,a4=8.77×1010,a5=4.58×108,a6=1.22×1016,a7=3.39×1014,a8=3.18×1012,a9=9.97×109。
动态轧制力参数a6变化时系统的幅频曲线,如图5所示。从图5可知,较大的三次刚度系数会使系统产生跳跃现象,但不会影响主共振的幅值。
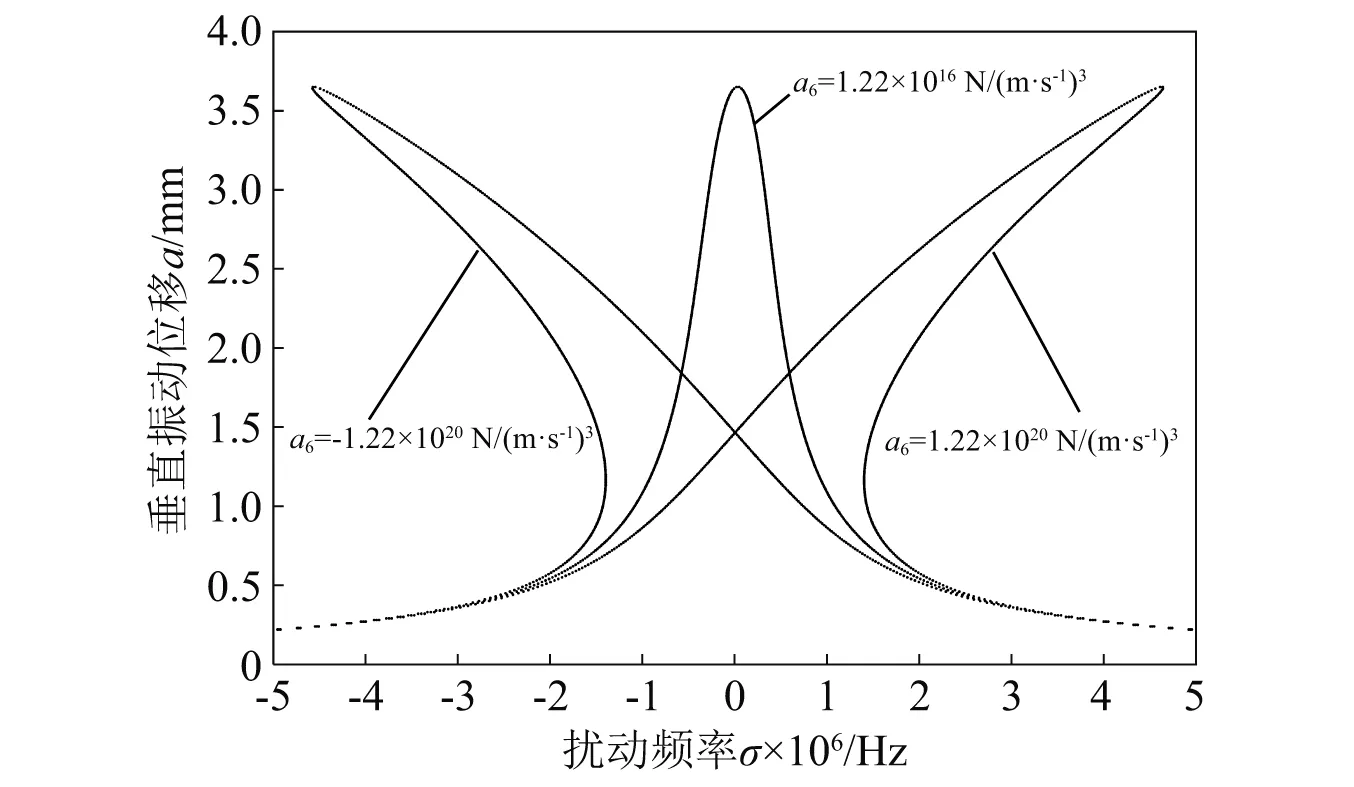
图5 参数a6变化时的主共振幅频曲线
外部扰动力幅值P0变化时系统的幅频响应曲线,如图6所示。从图6可知,外扰力幅值不仅会使系统产生跳跃现象,还会影响主共振幅值的大小。
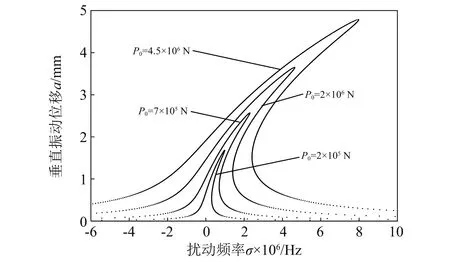
图6 外扰力幅值P0变化时的主共振幅频曲线
外部扰动力幅值P0变化时系统在垂直方向的全局分岔曲线,如图7所示。从图7可知,外扰力幅值的变化会使系统在倍周期运动和混沌运动之间相互转换。
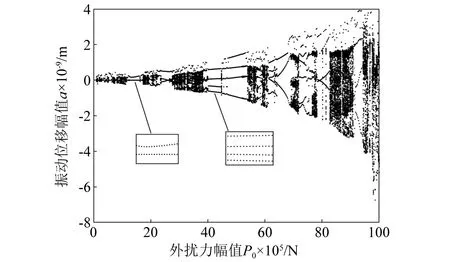
图7 外扰力幅值P0变化时的分岔图
入口油膜厚度z0变化时系统在垂直方向的全局分岔曲线,如图8所示。从图8可知:当k=1.3×1011N/m时油膜厚度的变化会使系统的运动状态更加复杂、不稳定;当k=1.08×1011N/m时,系统为2倍周期运动,油膜厚度的变化不会影响系统的运动状态。比较图8(a)和图8(b)可知,合适的刚度会使系统对变化的油膜厚度不再敏感。
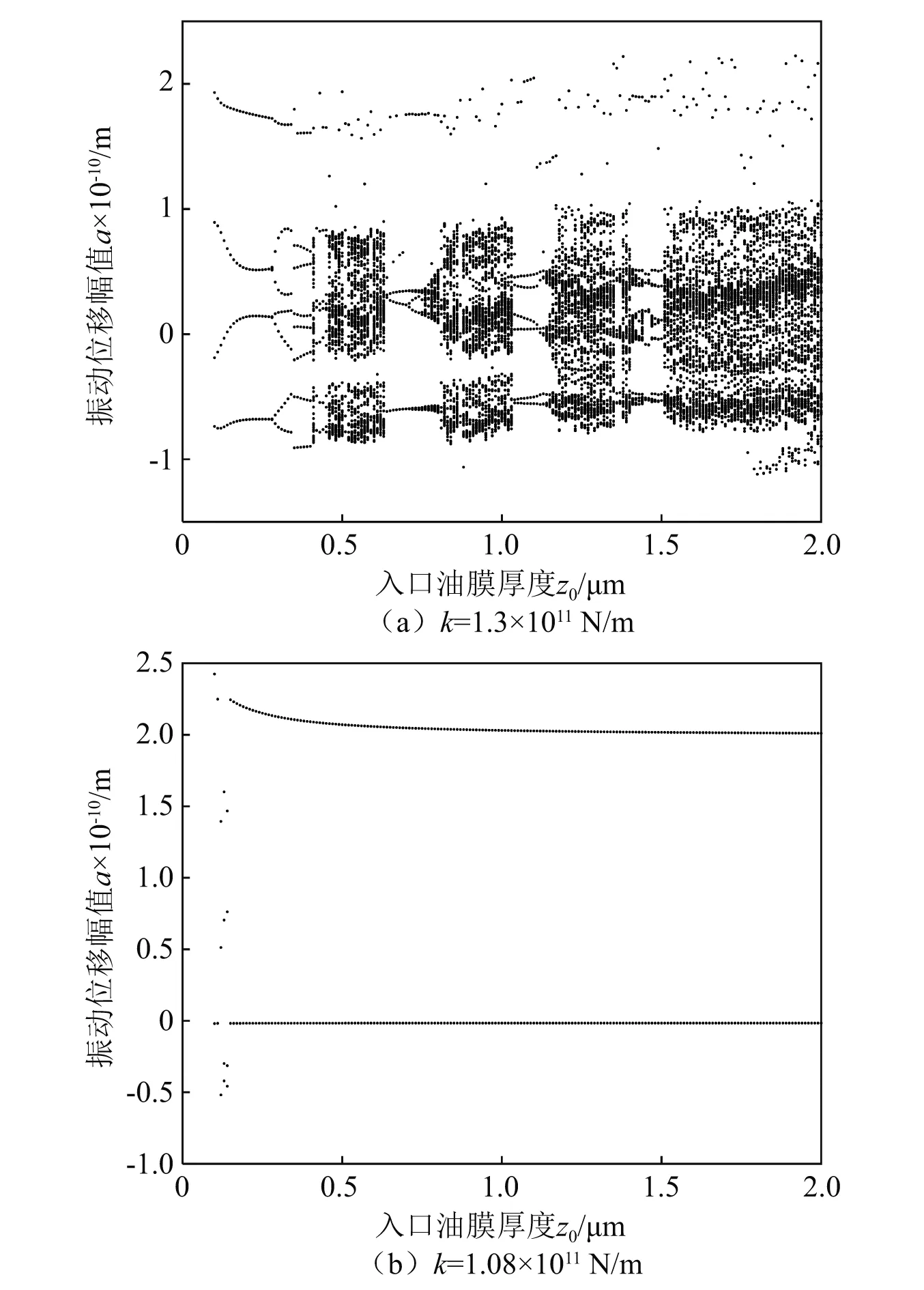
图8 入口油膜厚度z0变化时的分岔图
系统的相图和Poincare截面图,如图9~图11所示。
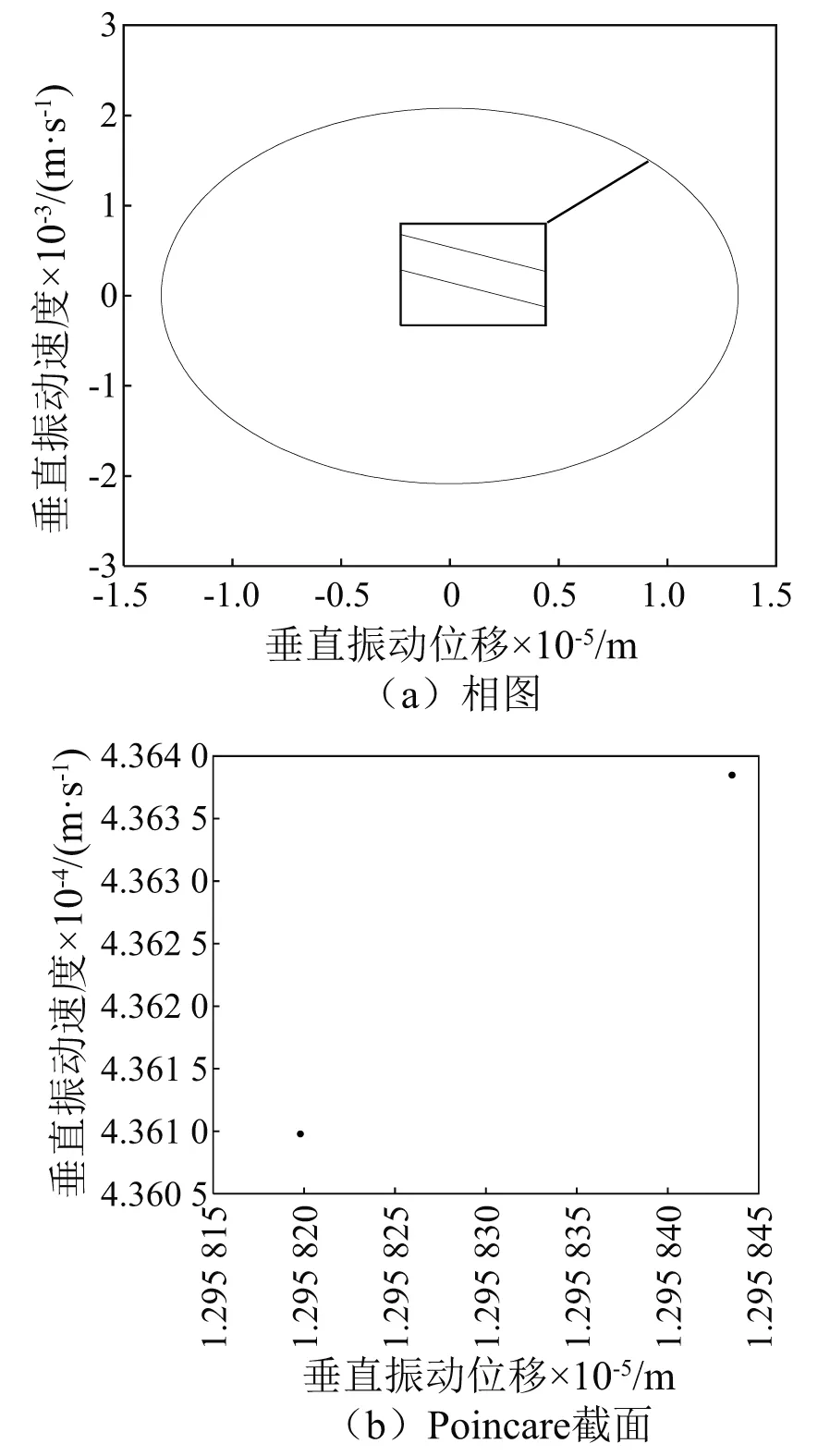
图9 P0=1.6×106 N时垂直方向的周期运动
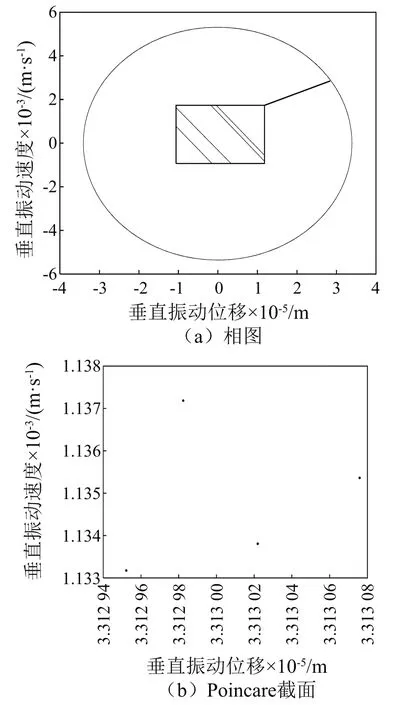
图10 P0=4.1×106 N时垂直方向的周期运动
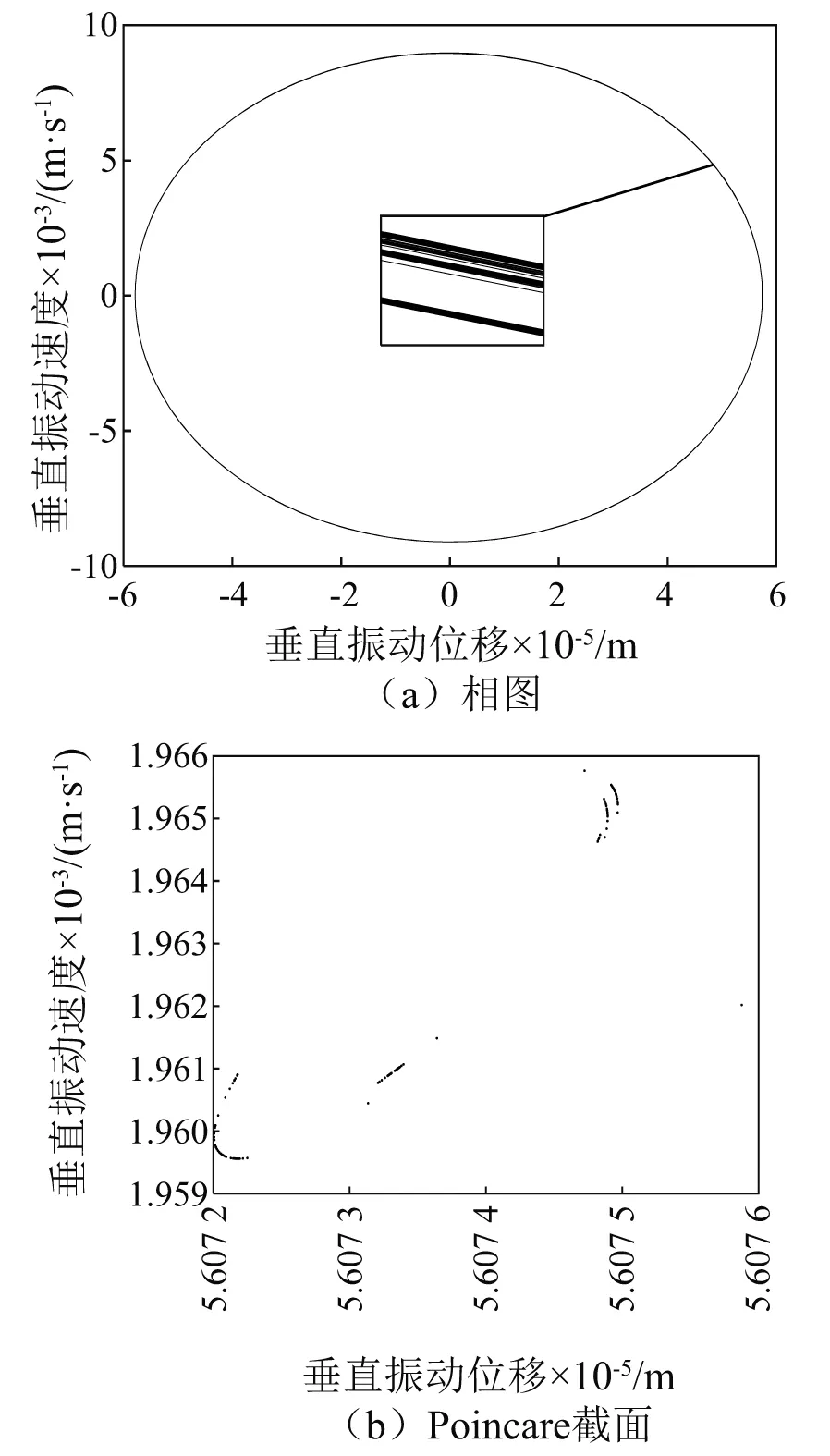
图11 P0=6.96×106 N时垂直方向的混沌运动
在图9中,相图为2条封闭的曲线,Poincare截面为2个点,说明系统是二倍周期运动;在图10中,相图分别为4条封闭的曲线,Poincare截面分别为4个点,说明系统是4倍周期运动;在图11的Poincare截面图可看到许多杂乱无章的点,说明系统处在混沌运动状态。
5 结 论
(1)通过将Karman微分方程中的干摩擦模型替换为混合润滑摩擦模型,建立了混合润滑摩擦状态下轧机辊系垂直振动模型,并得到了与入口油膜厚度有关的动态轧制力表达式。
(2)动态轧制力参数a6增大,系统会出现跳跃现象;外扰幅值P0的变化同时影响着系统的主共振幅值大小和系统的跳跃性。因此,可以通过降低外部扰动力来减小轧机振动幅值,减小振动带来的危害。
(3)改变外部扰动力幅值,系统会在周期运动和混沌运动之间相互转换;当k=1.3×1011N/m时,入口油膜厚度的变化会影响系统的运动状态;当k=1.08×1011N/m时,系统的运动状态不受入口油膜厚度变化的影响,系统更加稳定。
