前缘扰流体对水中流激空腔振荡影响的数值研究

章文文，徐荣武

(1.海军工程大学 振动与噪声研究所，武汉 430033；2.海军工程大学 船舶振动噪声重点实验室，武汉 430033)

流体以一定速度流经结构表面的开口部位时，边界层在开口前缘脱落形成具有振荡性质的自由剪切层，自由剪切层撞击后缘又会向前缘产生压力波反馈，满足一定的相位关系，自由剪切层将产生稳定的周期性自持振荡，即流激空腔振荡，产生很强的脉动压力并辐射单根或多根被称为“空腔纯音”的线谱噪声。典型的开口部位如飞机弹舱[1]、舱形起落架[2]、潜艇流水孔[3]甚至管道阀门[4]都可能存在强烈的流激空腔振荡现象，对声学性能甚至是结构疲劳强度都有着较大危害，且流激空腔振荡问题的几何模型简单，但产生机理却包含了丰富的物理、声学甚至是控制理论元素，因此流激空腔振荡也一直是流体力学和流致声学领域的热点问题，也是历久弥新的问题[5]。

流激空腔振荡的控制方法根据是否有外界能量输入，可以分为主动控制和被动控制，其中主动控制方法大抵有以下四类：一是通过空腔前缘下方的外部射流减小腔口剪切层与空腔内部流体的速度梯度，减弱剪切层振荡的发展[6]；二是在空腔前缘布置类似飞机襟翼的振荡板，通过前缘振荡板影响腔口的涡脱落，进而减缓腔口的剪切层振荡[7]；三是在空腔后缘的壁面上布置激振器，干扰剪切层拍击腔口后缘产生压力脉动，破坏腔口剪切层自持振荡的反馈环[8]；四是在腔口前缘布置零质量射流器，这类控制方式与第一类前缘射流控制方式相近，但没有外部流体输入[9]。虽然这些主动控制方法往往能有效抑制空腔振荡，但几乎都只适用于较高马赫数的空腔流，而对于水中流速通常为极低马赫数(Ma<0.01)的情况，还未见有相关的主动控制研究，因此，对于水中流激空腔振荡控制，被动控制方法仍不失为一种可靠、有效的途径。

相较于主动控制，被动控制具有结构简单，效果稳定可靠等优势。流激空腔振荡的被动控制方法一般是通过在腔口的前缘或后缘设置扰流体或改变其形状来实现，Bolduc等[10]和Omer等[11]分别分析了空腔前缘和后缘的几何形状对空腔流激声共振的影响，试验结果表明改变后缘几何外形可以有效抑制流激空腔共振，但不能完全消除，而具有良好外形的前缘可完全抑制空腔声共振的发生；宁方立等[12]提出一种可变形状的空腔结构模型，这种空腔结构可以通过调整后壁面倾斜角抑制空腔振荡和噪声；Saddington等[13]对比研究13种不同被动控制措施对空腔噪声的抑制效果，结果表明扰流体相对于改变空腔形状有更好的空腔噪声抑制效果，而前缘扰流体又优于后缘扰流体效果，其中，前缘锯齿单元对空腔振荡的抑制效果最好；梁勇等[14]进一步对锯齿单元不同安装角度的空腔噪声抑制效果进行了研究；McGrath等[15]最早介绍了一种在腔口前缘上方放置圆杆的控制装置，可以显著抑制空腔声共振；Flaherty等[16]对这种圆杆扰流棒和其他三种扰流体的空腔声共振控制效果进行对比研究，结果表明圆杆扰流棒的抑振效果最好；Sarpotdar等[17]的研究结果指出圆杆扰流棒对空腔共振线谱声的抑制效果与圆杆和前缘之间的间距以及圆杆直径相关。总体而言，在空腔前缘放置的锯齿单元或圆柱扰流棒是目前提出的较为高效的空腔振荡被动控制装置，但其控制效果一般受限于设计点速度，在偏离设计点速度的情况下控制效果变差，同时，对结构表面的流线型有一定的破坏，往往会引起阻力增加。

本文提出一种新型空腔振荡被动控制方法，即在空腔前缘的后上方一定高度处放置一倒楔形块，本文称其为前缘分流体(leading-flow division，LFD)，前缘分流体在空腔前缘位置将一部边界层流体分流至腔内，一方面可以降低腔口剪切层的速度梯度；另一方面减少了剪切层内大尺度涡的分布，进而减弱自由剪切层与空腔后缘的碰撞强度，最终达到抑制空腔振荡的目的。前缘分流体三维结构，如图1所示。

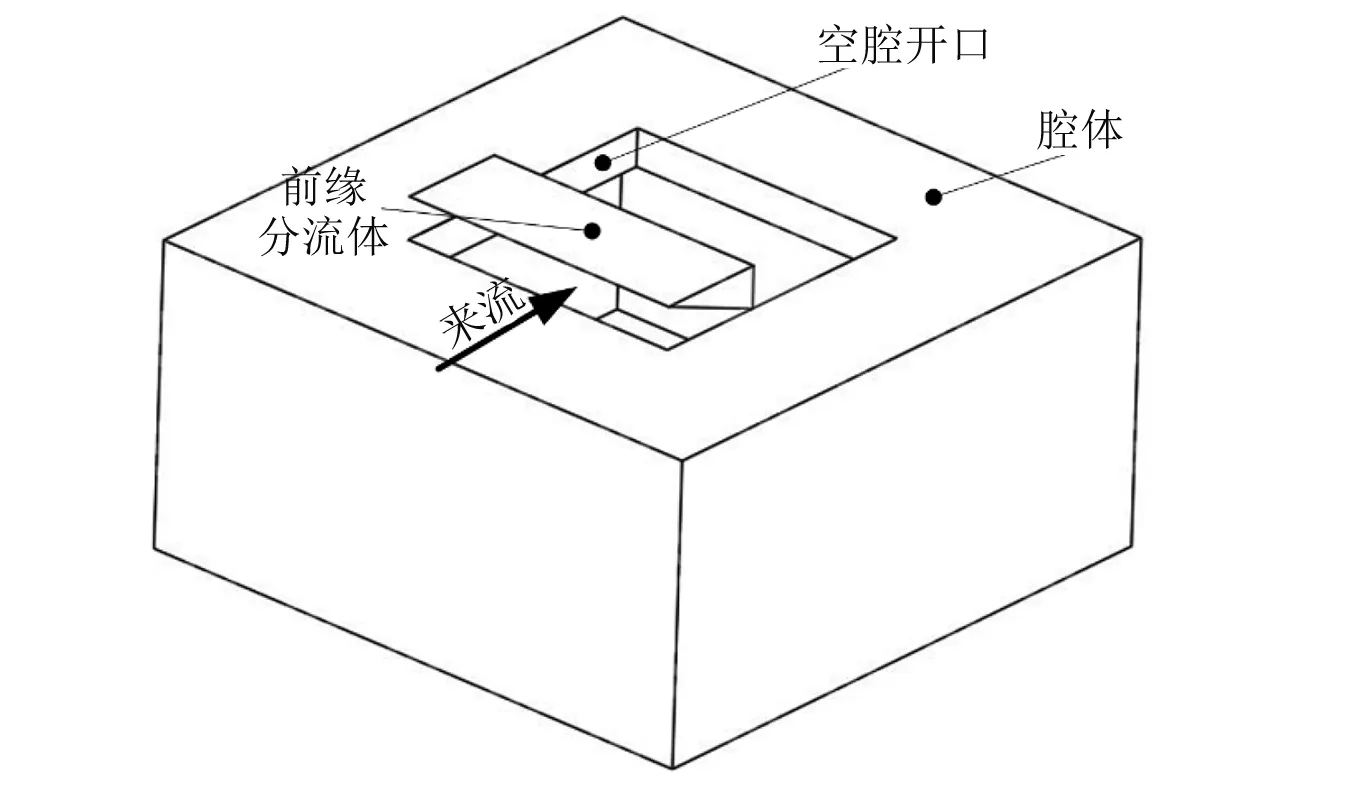
图1 前缘分流体三维结构

1 数值计算方法

本文采用大涡模拟(large-eddy simulation, LES)方法，对空腔流场和壁面脉动压力进行数值模拟。大涡模拟的基本思想是通过空间滤波，将计算流场域中的涡团分离为大、小两种尺度，其中，大尺度涡支配着湍流的整体动量和能量的运输，代表了湍流的平均流动，而小尺度涡一方面则主要负责湍动能的耗散作用，同时还又对大涡有反馈作用。基于这种想法，LES方法用非稳态的Navier-Stokes当成直接求解大尺度涡运动，对小尺度涡的运动则采用亚格子模型进行模拟。

应用滤波函数可将湍流中的瞬时流动变量分为两部分，对瞬时变量φ有如下形式

(1)

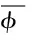
(2)

式中：D为流场计算区域；x′和x分别为大尺度涡在滤波前和滤波后的空间坐标；G(x,x′)为滤波函数，决定了所求解的涡的尺度，在有限体积法中，G(x,x′)采用如下表达式

(3)

式中，V为计算网格的体积。

用式(2)表示的滤波函数处理瞬态下的连续性方程和Navier-Stokes方程，可以得到LES方法的控制方程组

(4)

(5)

式(4)和式(5)还不能直接求解，需要构建亚格子尺度(subgrid scale, SGS)应力的数学表达式才能进行求解。最早的SGS模型由Smagorinsky[18]提出，其基本的SGS模型的形式为

(6)

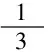
(7)

最初的Smagorinsky亚格子模型由于常数固定，容易降低平均剪切层及近壁边界层中大尺度涡的脉动，进而造成流场精度不够。1991年，Germano等[19]提出一种动态亚格子应力模型，这种模型通过动态计算涡黏性系数来尽可能的反映实际流动情况；1992年，Lilly[20]利用最小二乘法对此模型进行了改进，该亚格子动态模型的涡黏性系数由式(8)计算

(8)

式中：Lij为网格滤波与测试滤波之间的亚格子尺度应力差值，测试滤波即为反映亚格子动态特性的二次滤波；Mij为与滤波宽度和应变率张量有关的中间量。

经Lilly改进后的动态亚格子模型被称为动态Smagorinsky-Lilly亚格子模型，该亚格子模型的常数在时间和空间上都有一个相对宽泛的范围，从而避免了数值模拟的不稳定性。本文的数值模拟即采用动态Smagorinsky-Lilly亚格子模型，其具体推导参见Germano等和Lilly的研究。

2 数值计算模型

2.1 几何模型及计算域

本文模拟的基准空腔为开孔空腔，开孔长宽尺寸为L×W=50 mm×50 mm，空腔深度D=50 mm，L/D=1，为深腔，开孔平板厚5 mm。为保证空腔前缘来流边界层厚度，以及后缘尾流的充分发展，腔口上游、下游流动尺度取为8L。基准空腔几何模型和计算域，如图2所示。

图2 基准空腔几何模型和计算域(mm)

前缘分流体安装在前缘的后上方，分流体的主要尺寸参数为安装高度h和分流角θ，安装高度h=δ/2，δ为前缘位置处的来流边界层厚度，分流角θ=15°。当来流速度U为7 m/s时，空腔前缘位置处的流向速度随高度变化曲线，如图3所示，工程上通常将边界层内速度u=0.99U时的法向距离定义为边界层厚度，因此可以判定边界层厚度δ=6.0 mm。前缘分流体的尺寸示意图，如图4所示。

图3 前缘平面流向速度分布

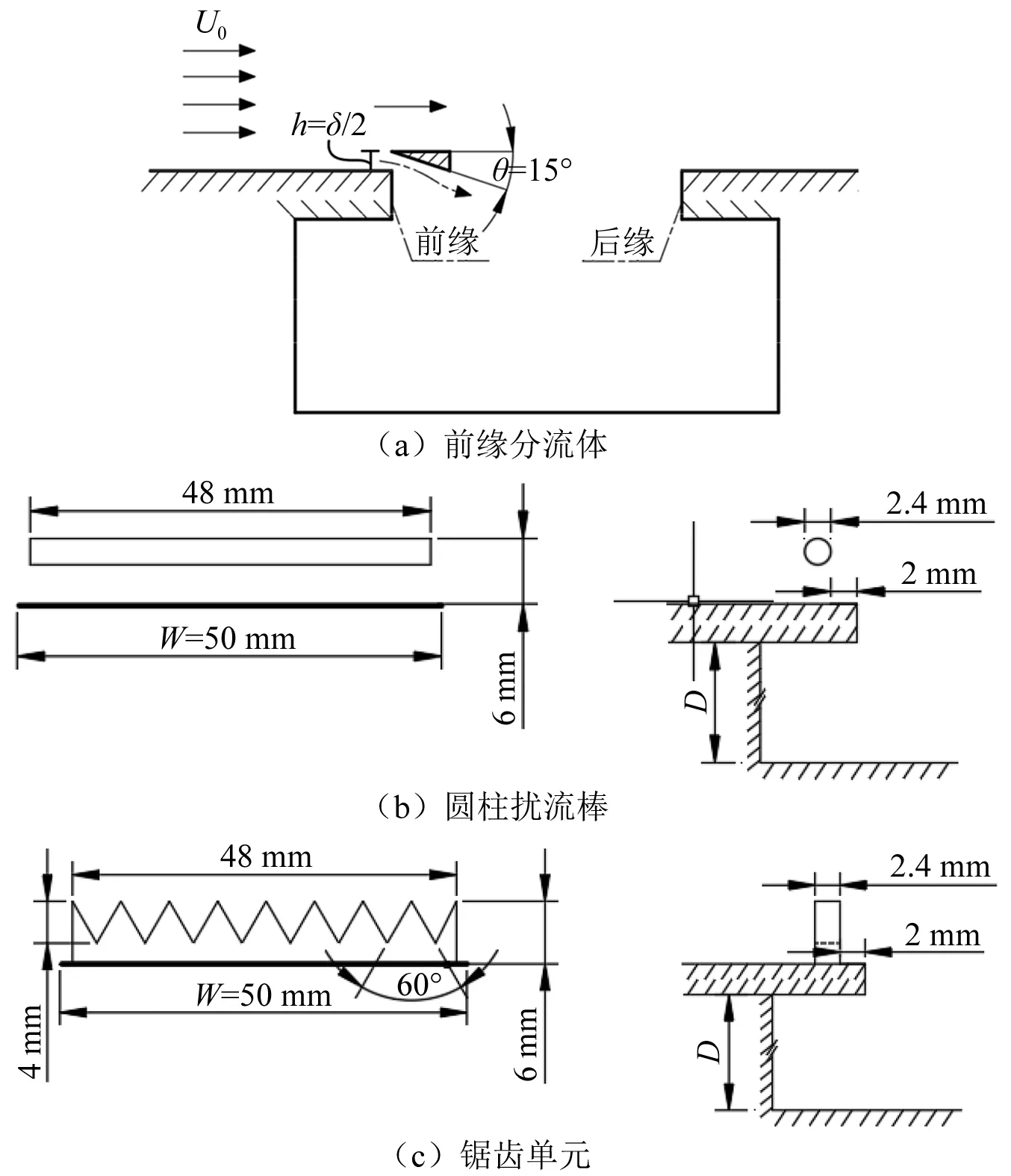
图4 三种不同前缘扰流体的尺寸参数

为对比分析前缘分流体对空腔振荡的抑制效果，本文同样对圆柱和锯齿形两种扰流体的空腔振荡抑制效果进行了分析。文献[21]指出，扰流体高度越接近边界层厚度控制效果越好，圆柱绕流棒直径为40%边界层厚度时噪声抑制效果最好，为对比三种扰流体的抑振效果，设置三种扰流体的尺寸参数见图4。

2.2 流场网格划分及边界条件

由于空腔流动的几何模型较为简单，本研究对整个流场计算域采用非均匀结构网格，在空腔开口和空腔内部网格划分较为细密，随着与腔口距离的增加网格逐渐稀疏。为准确捕捉绕流边界层和剪切层的流动信息，在绕流壁面和扰流体附近均采用边界层网格，壁面第一层网格尺度为5×10-3mm，相应无量纲高度y+≈1，沿壁面法向的网格节点外扩比例控制在1.1～1.2左右，各空腔模型的流场网格数量约为1.6×106～2.4×106左右(基准空腔网格数量最小，含锯齿单元空腔网格数量最大)。各模型的流场网格划分,如图5所示。

图5 网格划分示意图

边界条件设置如图6所示。来流边界设置为速度入口，速度定义为均匀法向速度；出流边界设置为自由出流，出口相对压力为零；空腔结构及扰流体表面均设置为无滑移固体边界，u=v=w=0;其余边界设置为自由滑移壁面边界，即流场边界法向的速度梯度和压力梯度为零，保证边界内外流体性质的一致性。

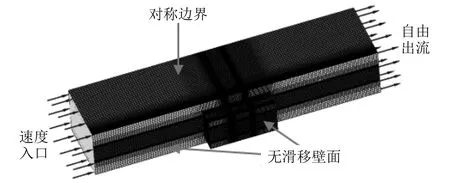
图6 空腔流场网格及边界条件

2.3 求解设置

本文采用Arunajatesan等[22]提到的一种RANS-LES混合计算方法,即先采用RANS模型进行定常模拟，流场稳定后，再紧接着采用LES模型进行非定常计算，该方法可以节省计算时间，且无需舍去LES计算过程中初始非稳定状态的部分结果。本文RANS定常计算收敛残差值设定为1×10-5，步数为1 000 步，计算结果表明在该计算步数内，空腔绕流场达到稳定的时均定常状态。

本文模拟的空腔流动介质为5 ℃的水，动力黏性系数为1.519×10-3kg/m·s-1，密度为1 000 kg/m3，流体介质声速为1 500 m/s，模拟来流速度为7 m/s。大涡模拟的时间步长Δt=5×10-5s，计算步数N=10 000，大涡模拟计算过程中记录每个时间步的空腔及扰流体结构表面的脉动压力数据，并将每个时间步的表面脉动压力数据作为声场计算的偶极子表面声源。根据快速傅里叶变换，可知求解的最高计算频率fmax=10 000 Hz和频率分辨率Δf=2 Hz。

流场计算中，为对比各扰流体对空腔流动的影响，分析空腔流动控制规律，在空腔流向中心平面的前缘、腔口中心、后缘和腔底中心分别设置三个压力脉动监测点，并分别标记为P1，P2和P3，压力监测点位置如图7所示。

图7 流场脉动压力监测点

3 结果与分析

水介质中的空腔往往为水面或水下航行器的流水孔结构，为保证流水孔足够的透水速度，通常对孔口出流面积有一定的要求，本文所研究圆柱扰流棒和锯齿单元均对孔口出流面积无影响，而前缘分流体则一定程度上会减小孔口的出流面积，为更为合理地分析前缘分流体的空腔噪声控制效果，本文同时也对等孔口面积的前缘分流体空腔模型进行了数值模拟，该空腔模型孔口流向长度l由50.0 mm增加为55.4 mm，保证孔口出流面积与基准空腔一致。

为简化计算结果分析过程的文字表示，本文以BC(basic cavity)表示基准空腔模型，以RS(rod spoiler)表示圆柱扰流棒空腔模型，以STS(saw-tooth spoiler)表示锯齿单元空腔模型，以LFD表示前缘分流体空腔模型，以EA-LFD(equal area-leading-flow division)表示等孔口面积的前缘分流体空腔模型。

3.1 脉动压力对比分析

本文在图7所示的三个监测点P1，P2和P3,分别监测空腔前缘、后缘和底部的脉动压力变化，其中底部监测点P3的脉动压力常被用来表示空腔噪声。为分析空腔脉动的频域特性，对仿真得到的各监测点的脉动压力信号做快速傅里叶变换，并按声压级的定义将脉动压力幅值表示为脉动压力级，以便于分析，脉动压力级计算公式为

(9)

式中：LSP(f)为脉动压力级，dB；pref为脉动压力参考值，取水声学声压基准值1×10-6Pa。

空腔振荡的主要特征表现为壁面脉动压力频谱的离散窄带峰，从图8给出的基准空腔在流速为7 m/s时的脉动压力频谱可以发现，基准空腔的前缘(P1点)、后缘(P2点)和腔底(P3点)的脉动压力频谱均在76 Hz处具有突出的线谱峰，根据张翰钦等[23]针对水中不可压缩流动特点修正的空腔自持振荡频率预报公式，如式(10)所示，本文研究的空腔模型在7 m/s流速激励下产生的一阶振荡频率理论计算结果为74.4 Hz，与本文仿真结果误差仅为2%，表明本文数值仿真结果可信。同时,图8中没有其他频率的线谱，这表明在该流速下，基准空腔只产生了一阶振荡模态。

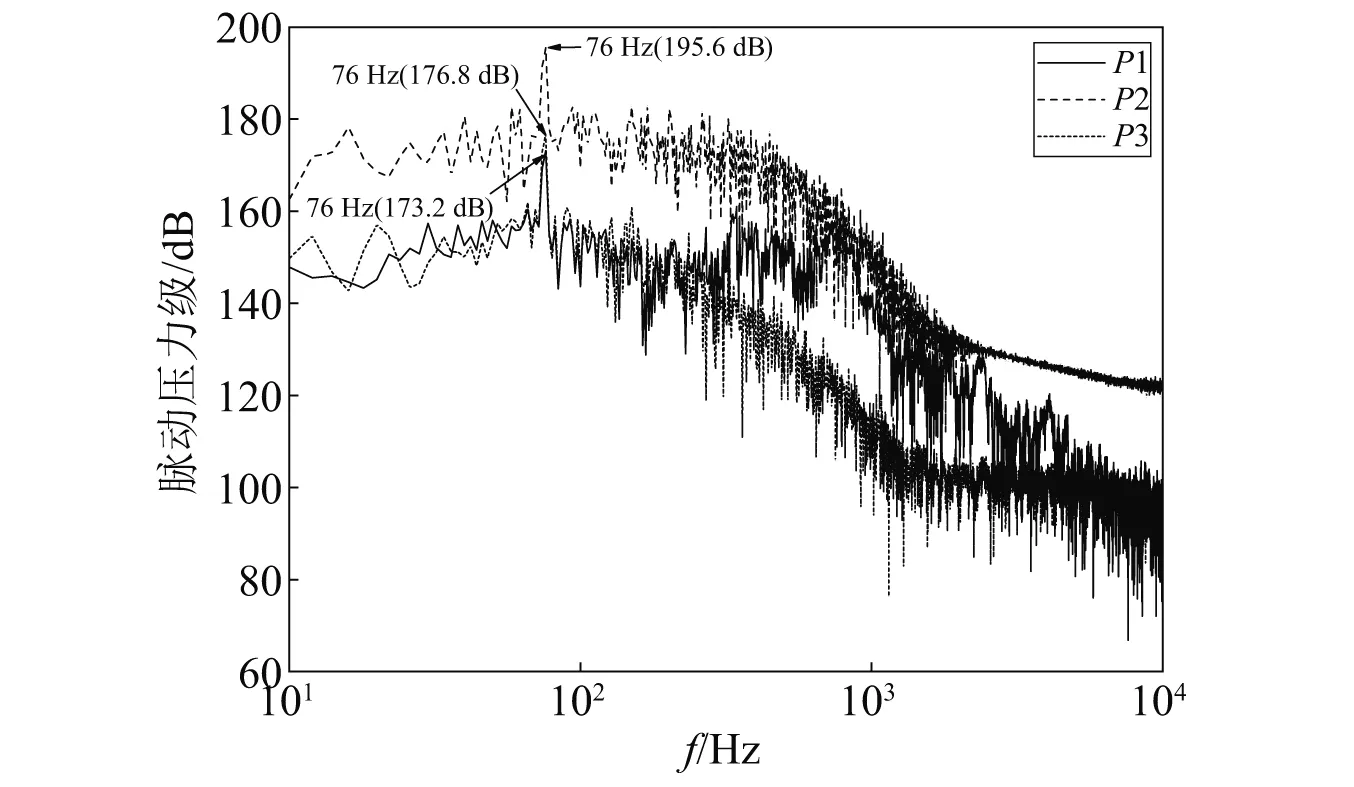
图8 基准空腔脉动压力频谱

(10)

式中：fn为流激空腔自持振荡频率；L为空腔开口在流动方向的长度；U为来流速度。

从基准空腔脉动压力频谱可以看出，后缘脉动压力要显著大于前缘以及腔底脉动压力，同时，最能表征空腔噪声辐射特性的腔底脉动压力谱线与后缘脉动压力谱线很相似，这一定程度上也印证了后缘是空腔噪声的主要声源部位；从脉动压力级的频率分布可以看出，脉动压力在10～1 000 Hz频段要远大于1 000 Hz以上频段，经计算，P1，P2和P3三个监测点在10～1 000 Hz频段内的脉动压力能量均超过了总计算频段内脉动压力能量的99%，与水动力噪声能量主要集中在低频段的实际情况相符，因而后续只在10～1 000 Hz频段内分析扰流体对空腔脉动压力的影响。

图9～图11分别给出了空腔前缘(P1点)、后缘(P2点)和腔底(P3点)三个位置处的脉动压力仿真计算结果，分别如图9～图11所示。为突出前缘扰流体对空腔脉动压力的影响，将安装不同前缘扰流体的空腔脉动压力频谱曲线与基准空腔脉动压力频谱曲线放置在同一频谱图中，以形成对比。

图9 空腔前缘脉动压力频谱对比

图10 空腔后缘脉动压力频谱对比

图11 空腔底部脉动压力频谱对比

图9为安装不同前缘扰流体的空腔在前缘监测点P1的脉动压力频谱。从图9中可发现，除圆柱扰流棒外，锯齿单元、前缘分流体和等开口面积前缘分流体均有效抑制了前缘脉动压力的线谱和连续谱分量，而圆柱扰流棒仅对其线谱分量有一定的抑制效果(由170.8 dB降低至164.9 dB)，但对连续谱分量却引起了较大幅度的增加，这可能是由于前缘上方的圆柱脱落的卡门涡旋引起的。同时，可以发现锯齿单元对前缘脉动压力的连续谱分量，特别是较高频段的连续谱，具有最为显著的抑制效果；此外，前缘分流体几乎消除了空腔前缘的脉动压力线谱，这表明前缘分流体有效破坏了腔口声反馈环。

图10给出了各空腔模型在后缘监测点P2处的脉动压力计算结果，从频谱分析可以发现，四种前缘扰流体均对后缘脉动压力的线谱分量有较为明显的抑制作用，其中，前缘分流体对线谱的抑制效果最好，和在前缘处的抑制效果相似，几乎消除了线谱分量；圆柱扰流棒、锯齿单元和等开口面积前缘分流体则分别将后缘脉动压力线谱分量由原来的193.1 dB降至183.8 dB，180.4 dB以及180.5 dB。同时可以发现，圆柱扰流棒、锯齿单元和前缘分流体三种前缘扰流体几乎使后缘脉动压力的频谱曲线在无扰流体的频谱曲线之下，而等开口面积的前缘分流体却使后缘脉动压力频谱曲线与无扰流体的频谱曲线在连续谱分量上大致相当，这表明空腔开口的流向尺度也是前缘分流体对空腔噪声控制效果的重要影响参数。

图11为空腔底部中心P3点在不同前缘扰流体作用下的脉动压力频谱图，由于腔底的脉动压力常用来表征流激空腔振荡和噪声特性[24]，因而，图11所示的脉动压力频谱更能反映前缘扰流体对流激空腔噪声的抑制效果。从图11中可以看出，四种前缘扰流体均显著降低了腔底脉动压力的线谱强度，其中，前缘分流体同样几乎消除了腔底脉动压力线谱，而圆柱扰流棒、锯齿单元和等开口面积前缘分流体虽然分别降低线谱幅值7.5 dB，11.5 dB和13.3 dB，但腔底脉动压力仍然还存在较为明显的主导峰值，且主导峰值频率向低频移动，相对于基准空腔的主模态频率分别减小8 Hz，4 Hz，4 Hz，这意味着空腔声共振可以在更低的流速下发生。此外，需要注意的是，在主导峰值频率前的低频段，圆柱扰流棒和锯齿单元引起了一定程度的腔底脉动压力的升高，而前缘分流体(无论是否改变腔口面积)则使腔底脉动压力几乎在所有频段都有所降低。从图11所示的计算结果不难发现，前缘分流体对流激空腔振荡具有相对最好的抑制效果，但在保持等开口面积的情况下，其对空腔振荡的抑制效果有所降低。

3.2 流场特性对比分析

3.2.1 速度特性

为分析不同前缘扰流体抑制空腔振荡的机理，本文对仿真计算所得到的速度分布和涡量等流场特性进行了对比分析。流动时间t=0.4 s时刻的各空腔模型在流向中间剖面的速度分布情况，如图12所示。从图12(a)所示基准空腔速度分布可以明显地看出，前缘前部平稳、细薄的边界层在经过腔口时，其厚度逐渐扩大，发展成具有振荡性质的剪切层，并最终与后缘碰撞，一部分剪切层流体向后缘后部流动；另一部分流体则沿后缘流入腔内，从速度矢量分布可以看出，腔口正下方形成较为明显的涡旋；在图12(b)中可以发现，来流在流经圆柱扰流棒时，其后方脱落的涡旋与剪切层相混合，增大了剪切层厚度，同时也衰减了腔口剪切层的振荡；在图12(c)中可以发现，锯齿单元抬升了腔口剪切层，使剪切层近乎跨过腔口进而与后缘后部发生碰撞，需要注意的是安装锯齿单元的空腔，其后缘后部的速度分布相较于基准空腔更为不均，且腔内的涡旋没有得到明显的改善；在图12(d)中可以发现，经过前缘分流体的来流所形成的剪切层沿腔口较为平稳的发展，振荡幅度较小，后缘后部的速度分布较为平稳，同时腔口正下方的涡旋也基本得到了消除，但当保证腔口面积不变而延长腔口长度时(见图12(e))，前缘分流体后的剪切层振荡幅度有所增加，且腔内的涡旋分布变得和基准空腔类似。

图12 空腔流向对称剖面的速度分布(白色箭头为归一化的速度矢量，t=0.4 s)

来流边界层流经腔口前缘时即发展为自由剪切层，剪切层是典型的不稳定流动，众多研究表明，剪切层振荡是空腔脉动压力以及空腔噪声的主要来源，为进一步探讨不同前缘扰流体对腔口剪切层的影响，本文对腔口x/L=1/4，x/L=1/2和x/L=3/4三个位置处的时均流向速度分布进行了计算，x为距腔口前缘的距离，L为腔口长度，如图13所示。

图13 腔口中间截面时均流向速度剖面

从图13可以看出，对于五种空腔模型，剪切层沿流向的发展具有相同的趋势，即剪切层随着流动向下游发展，其厚度逐渐增加，三种前缘扰流体均没有改变剪切层沿流向的发展规律，但在同一位置，不同前缘扰流体对剪切层的影响有较大差异。从图13中可以看出，锯齿单元对剪切层的影响主要是将其向空腔外部抬升，但对于剪切层厚度没有明显改变，而圆柱扰流棒相对于另外两种扰流体，则明显增大了腔口剪切层厚度；前缘分流体对腔口剪切层速度分布的影响较小，在一定程度上也增大了剪切层厚度，但其主要影响是使剪切层沿流向的发展变缓。由此从腔口剪切层的速度分布可以推知，锯齿单元主要通过将剪切层抬升来减小空腔振荡，圆柱扰流棒通过增大剪切层厚度来减弱空腔振荡，而前缘分流体则主要减缓了剪切层沿流向的发展，进而减弱空腔振荡。

3.2.2 涡结构特性

涡声理论指出，流致噪声和湍流脉动压力实际上与流体中的大尺度涡结构密切相关，因此，为从涡结构方面解释各前缘扰流体抑制空腔脉动压力(空腔噪声)的机理，本文采用Q判据对空腔流动中的涡结构进行识别，以此来反映各扰流体对涡结构的影响特点。Q判据中的Q值实际上是速度的二阶梯度张量，其数学表达为

(11)

式中：Ω为旋转运动的旋转率张量；S为应变率张量。

Q判据可以表示流体微元净转动相对于轴向变形的强弱，当某处Q值为很大的正值时，说明此处的旋转率占有绝对优势，即具有较强的涡结构，这样可以根据不同取值的Q识别不同强度涡的存在。当Q=1×105s-2时的涡分布情况，如图14所示，为便于观察空腔内部的高强度涡的分布特征，图14为沿流向对称面剖开的空腔半模。

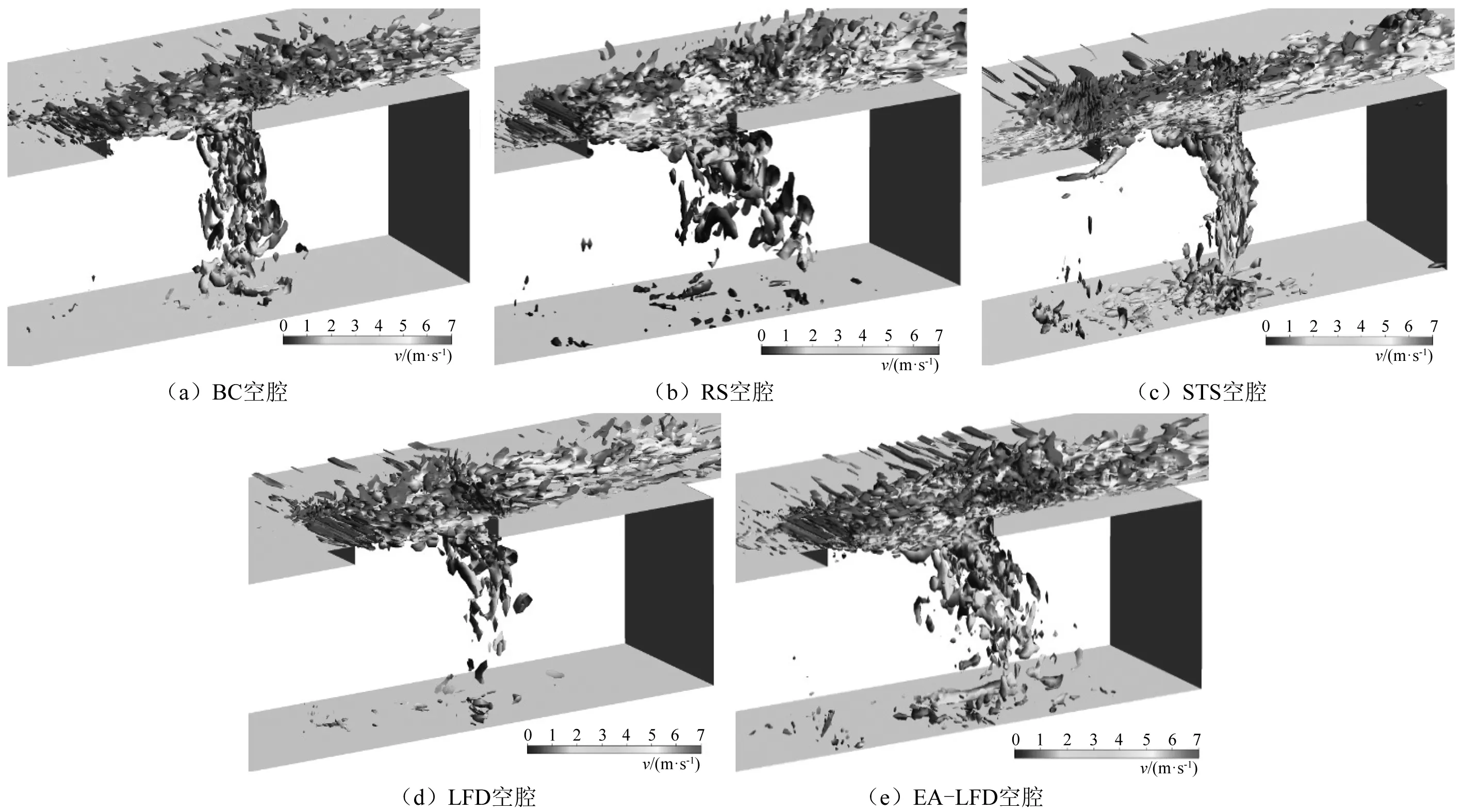
图14 空腔流动涡结构计算结果(Q=1×105 s-2)

从图14可以看出，空腔流动中的高强度涡结构主要分布在腔口剪切层、后缘下方以及后缘后部壁面附近。在图14(b)中可以发现，圆柱扰流棒产生的尾涡会与剪切层内的涡相混合，使腔口的涡层厚度有所增加，减小剪切层的速度梯度，这有利于腔口剪切层内的涡结构保持相对稳定，减弱大涡之间的配对、合并等相互作用，因而在腔口后缘未见有明显的碰撞涡结构；从图14(c)可以看出，锯齿单元将腔口的涡结构“打碎”成更多细小的涡结构，同时，腔口的涡团被向腔体外部抬升，可以推测正是由于这种对涡结构的“细化”和抬升作用，降低了剪切层与后缘的碰撞强度，从而显著减小了后缘处的脉动压力，但需要注意的是，在腔内以及后缘后方的高强度涡分布范围有较为明显的增大，这表明后缘后方的壁面脉动压力可能会有所升高；前缘分流体对空腔流场中的高强度涡的抑制效果最为明显，从图14(d)可以看出，前缘分流体减小了腔口涡层厚度，同时在腔内和后缘后方的高强度涡也明显减少，但随着腔口长度的增加，前缘分流体对这种高强度涡结构的抑制作用有所减弱(见图14(e))。

3.3 阻力计算结果分析

对于水下航行体而言，阻力通常是必须要考虑的性能参数之一，因而本文也对各空腔模型定常阻力进行了计算，定常流动的计算残差值设定为1×10-5，计算步数取为1 000 步，定常计算收敛后，各空腔模型的流动阻力(包括摩擦阻力和压差阻力)计算结果，如表1所示。

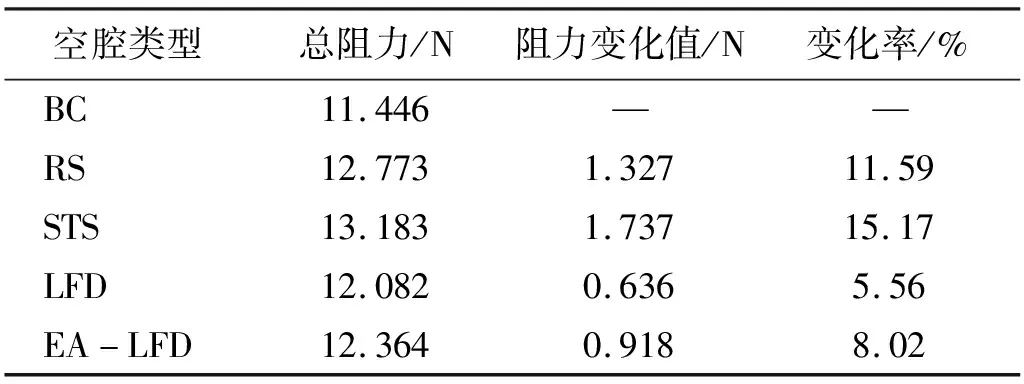
表1 各空腔模型阻力计算结果

从表1可以看出，圆柱扰流棒、锯齿单元和前缘分流体三种扰流体都会增加空腔受到的流动阻力，其中，锯齿单元对空腔流动阻力的影响最为明显，而前缘分流体对空腔流动阻力的影响最小，在保证空腔开孔出流面积不变的情况下，前缘分流体引起的附加阻力有所增加，但仍显著小于另外两种扰流体装置，这表明，从流动阻力方面考量，前缘分流体也是一种相对较为理想的空腔振荡被动控制装置。

4 结 论

本文采用大涡模拟方法研究了来流速度为7 m/s条件下，三种不同前缘扰流体对水中低速流激空腔振荡的影响，并对各前缘扰流体抑制空腔振荡的作用机理进行了讨论，通过综合分析得出以下结论：

(1)前缘分流体、圆柱扰流棒和锯齿单元均能有效抑制水中低速流激空腔振荡，相对而言，本文提出的前缘分流体对空腔振荡的抑制效果最为明显，几乎消除了空腔的自持振荡，降低腔底脉动压力线谱幅值达17.4 dB。

(2)不同前缘扰流体抑制空腔振荡的作用机理不同，前缘分流体主要是通过减弱腔口剪切层沿流向的发展，减少高强度涡分布，并消除腔内大尺度涡旋来抑制空腔振荡；圆柱扰流棒主要是通过其尾涡与腔口剪切层发生有益干涉，从而增大了剪切层厚度，减小速度梯度，有利于剪切层保持稳定，进而抑制空腔振荡；锯齿单元则主要是通过将前缘卷起的初生涡旋“打碎”成更多细小的涡结构，并将剪切层整体抬升，从而跨过腔口，避免与腔口后缘发生碰撞，进而抑制了空腔振荡。

(3)三种不同前缘扰流体都会引起空腔流动阻力的增加，但相对而言，本文提出的前缘分流体引起的附加流动阻力最小。

(4)随着腔口流向尺度的增加，前缘分流体对流激空腔振荡的抑制效果有所减弱。