基于吸振器控制的轧机辊系时滞反馈研究

刘 彬, 王营辉, 姜佳磊, 刘 爽

(燕山大学 电气工程学院,河北 秦皇岛 066004)

1 引 言

板带轧制产品在科研仪器、航天设备以及高精度仪表方面有着重要的应用,然而目前轧机生产过程中的振动问题严重制约了轧制水平的提高[1,2]。为了提高轧机设备运行的稳定性及轧制效率,对弹簧力非线性约束下加吸振器控制装置的轧机辊系稳定性及控制展开深入研究[3,4]。针对提高板带轧机的稳定运行的研究,提高轧机生产水平,刘彬等分析了轧件水平振动对轧制力和摩擦力动态特性的影响规律,仿真研究了轧件水平振动速度和轧机辊系振动位移随轧辊转速的变化规律[5];谢长贵等对工作辊周期内各阶段振动信号进行了分析研究,当轧制速度为中高速稳定轧制阶段时,工作辊对中间辊的相对运动形成工作辊表面振纹,该辊面振纹反作用于轧机,进而引起轧机强迫振动[6];侯东晓等研究了轧制过程中非线性条件约束下辊缝工作界面变摩擦力的影响规律,通过分析耦合系统幅频特性,得到轧机耦合系统随轧辊非线性刚度和外激励幅值变化规律[7];朱勇等研究了非线性弹簧力对轧机系统振动产生的影响,应用数值分析的方法得出轧机系统的分岔现象以及典型的非线性动力学行为[8];Tran等研究了液压缸的非线性特性,得到液压缸的非线性特性主要由液压缸内部摩擦系数非线性和液压缸等效刚度非线性共同导致的[9];范小彬等引入Duffing振子和参数激励的刚度函数,建立了一种轧机等效刚度非线性变化的轧机辊系振动模型,结合最大李雅普诺夫指数确定系统混沌运动状态,最后得到抑制轧机辊系振动的方法[10]。本文从轧机辊系机械结构进行考虑,利用吸振器装置的减振原理,通过在轧机系统上安装吸振器控制装置对轧机振动进行有效抑制,同时引入时滞反馈函数设计了系统的时滞反馈控制方程[11]。

本文以带吸振器控制装置的轧机辊系为研究对象,建立了非线性条件约束下的轧机辊系振动物理模型,引入时滞反馈控制函数,设计了带吸振器的轧机系统振动位移、振动速度的时滞反馈控制方程,通过仿真得到不同反馈增益参数和时滞量参数对轧机辊系主系统的影响规律,为抑制轧机振动提供了理论支持。

2 带吸振器控制装置的轧机辊系模型

轧机吸振器是通过弹性元件和阻尼元件把辅助质量连接到轧机主系统(轧机支架)上的减振装置,吸振器安装到轧机上辊系上后,二者构成一个两自由度系统,减振器在空间和结构上的安装情况如图1所示。轧机辊系和吸振器装置只做垂直方向的直线运动,在系统静止时轧机上辊系和吸振器装置的平衡位置为运动原点,轧机辊系和吸振器装置的振动位移的大小代表振动强度,为减小轧机辊系的振动,就需要减小振动位移;轧机辊系在简谐外激励作用下振动,轧机辊系的振动能量通过吸振器的弹性元件和阻尼元件转移到吸振器装置上,吸振器通过弹性元件和阻尼元件作用在轧机辊系上的作用力与外界对轧机辊系的作用力方向相反,从而把轧机辊系的振动能量转移到摩擦力中和吸振器装置的动能中,从而来减小轧机辊系的振动位移,达到抑制振动的效果。

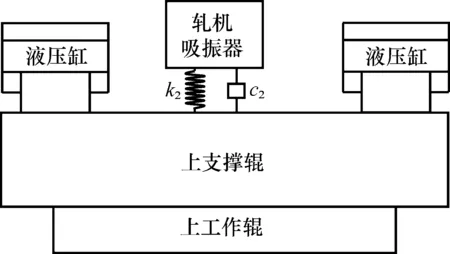
图1 安装减振器后的轧机辊系简图Fig.1 Rolling mill roll diagram after installing the damper

如图2所示,在轧机上辊系等效质量m1上安装一个动力吸振器m2,x1为轧机上辊系的绝对位移,x2为吸振器的绝对位移。图2中k1和c1分别为轧机上辊系和轧件之间的等效刚度和等效阻尼,k2和c2分别表示吸振器和轧机上辊系之间的等效刚度和等效阻尼。Fl(t)=Fsin (ωt)为等效负载力,其中F为外激励幅值,ω为外激励的角频率,Fs(x)为机械液压缸的弹簧力。

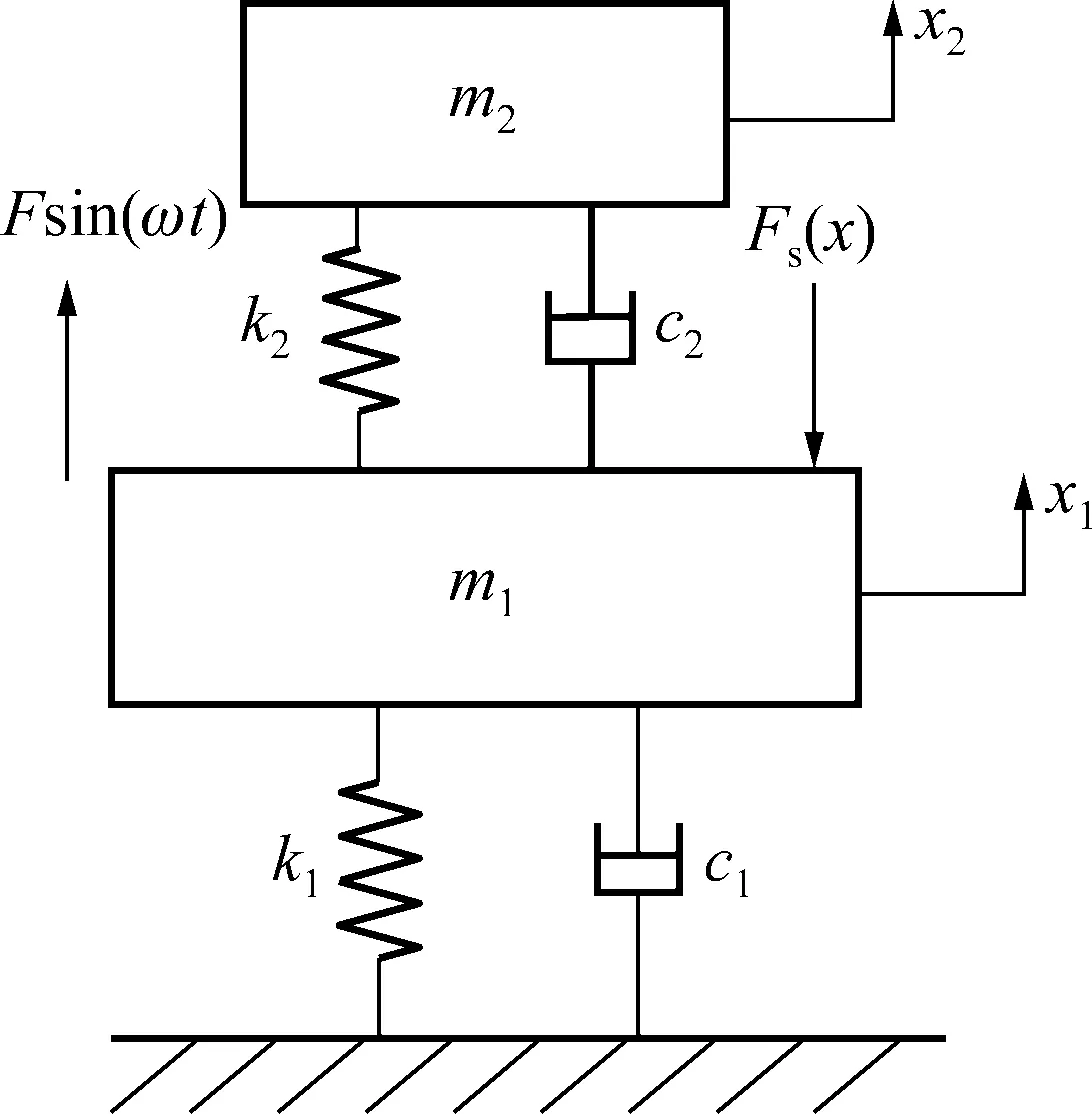
图2 带吸振器两自由度系统模型Fig.2 Two-degree-of-freedom system model with vibration absorber

轧机上辊系和吸振器以及轧机上辊系和轧件之间的等效刚度和等效阻尼为线性,液压缸的弹簧力是非线性的,系统模型的运动方程为:

(1)

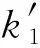
为了求得轧件轧辊耦合振动的幅频响应,近似认为轧机系统受到的外部激励具有周期性,通过移项和替换,将式(1)化成标准形式:

(2)

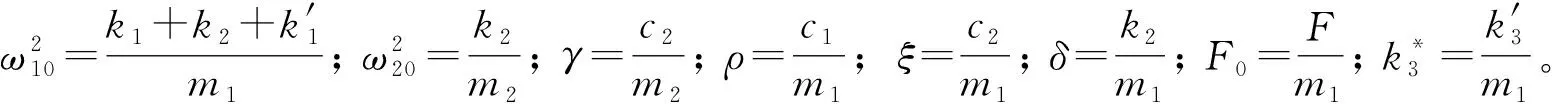
为了对轧机辊系垂直振动进行控制,引入振动位移和速度双时滞反馈函数,通过调节反馈增益系数和时滞参数,对带吸振器的轧机系统的不稳定振动控制效果进行分析,并且选择出最佳的参数组合,从而引入了时滞反馈控制函数:

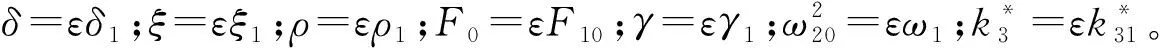
(3)

为了近似得到系统的计算结果,设立两种快变和慢变的时间尺度T0=t;T1=εt;对时间t的导数可写为采用多尺度法求解方程,只讨论一次近似解,设方程的解为:

(4)

将式(4)代入式(3),展开后令方程两端ε的同次幂系数相等,得到各阶近似方程:

(5)

(6)

将零次项方程组的解设为式(7)的形式,带入一次项方程组中得:

(7)

(8)

式中cc代表左边各项的共轭。

2.1 受控方程主共振响应求解

考虑系统主共振,ω10远离ω20,ω10无限接近θ,假设此时ω=ω10+εσ,其中σ为频率调谐因子。将ω=ω10+εσ代入式(8)中,消除久期项后得到:

(9)

为了求解方程,引入A1,A2的极坐标形式,A1=0.5aeiφ1,A2=0.5beiφ2,其中a,b,φ1,φ2都是时间T1的函数,引入中间变量θ=σT1-φ1,代入式(8)并分离实部和虚部得:

(10)

(11)

2.2 受控方程内共振响应求解

考虑内共振情况,假设ω=ω10+εσ,ω20=ω10+εσ1,其中σ、σ1为频率调谐因子,代入式(9),可得:

(12)

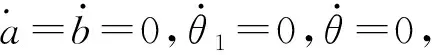
(13)

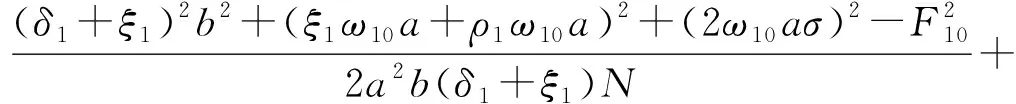
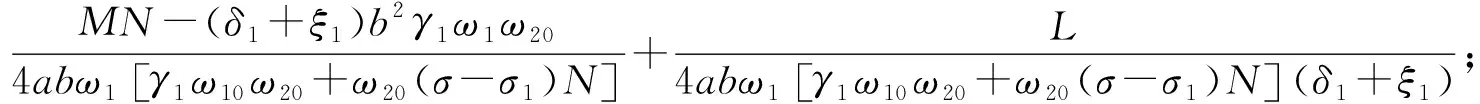
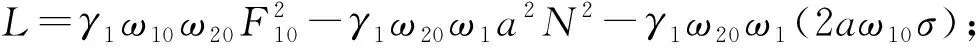
式(13)为引入时滞反馈控制函数之后的轧机辊系受控幅频方程。从幅频方程解的形式可以看出,轧机辊系的振动幅值受到外激励幅值和频率以及轧机参数等多种因素的影响,会造成系统的不稳定运行“跳跃现象”。引入时滞控制函数之后,可以通过调节控制参数,使得轧机辊系振动幅值的“跳跃现象”出现的频率区间变小,削弱轧机辊系低频振动幅值出现的“跳跃现象”,为提高轧机系统运行的稳定性提供了理论支持。

3 带吸振器的轧机辊系振动极限环幅值稳定性分析

时间历程曲线和相图是轧机辊系振动状态的直观体现,通过仿真图,可以判断轧机辊系振动的走势并做出适当的调整。轧机辊系的振动由于其自身具有的突发性和发散性特点,极有可能发生高频自激振动,对轧机系统的安全运行存在隐患。如果将轧机辊系的振动发散行为进行控制,使轧机辊系的极限环幅值收敛于一个较小的范围,这也就在一定程度上增强了系统的稳定性。因此,首先对轧机辊系振动的极限环幅值的稳定性控制效果进行检验,比较控制参数变化对轧机辊系稳定性的影响。图3和图4为非受控的轧机辊系振动特性仿真,图5和图6为g1=10 000,g2=50,τ1=0.75T,τ2=0时(工况1)的轧机辊系振动特性,图7和图8为g1=15 000,g2=50,τ1=0,τ2=0.75T时(工况2)的轧机辊系振动特性。时域图和相图如图3到图8所示。

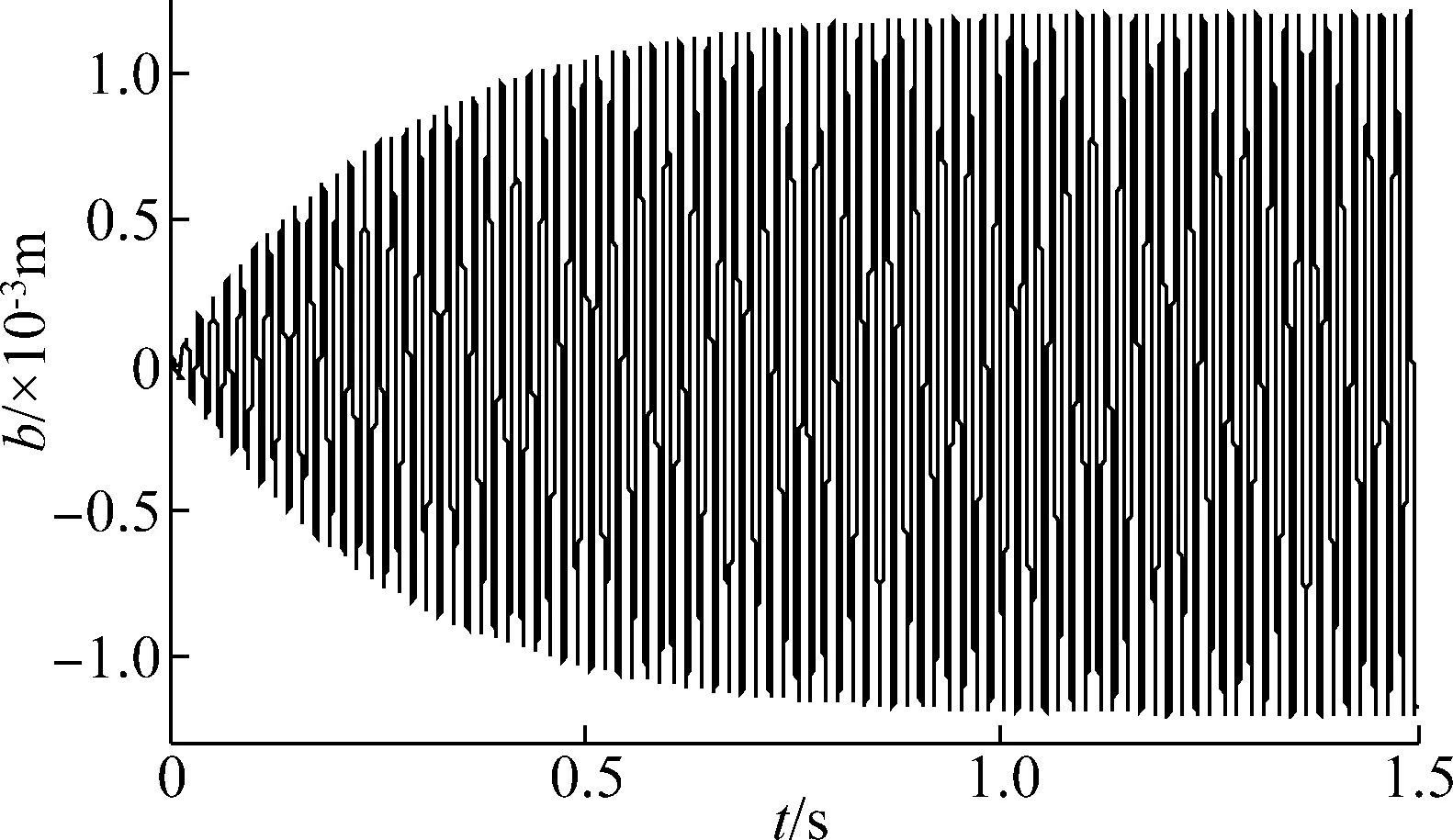
图3 非受控的时域图Fig.3 Uncontrolled time domain diagram

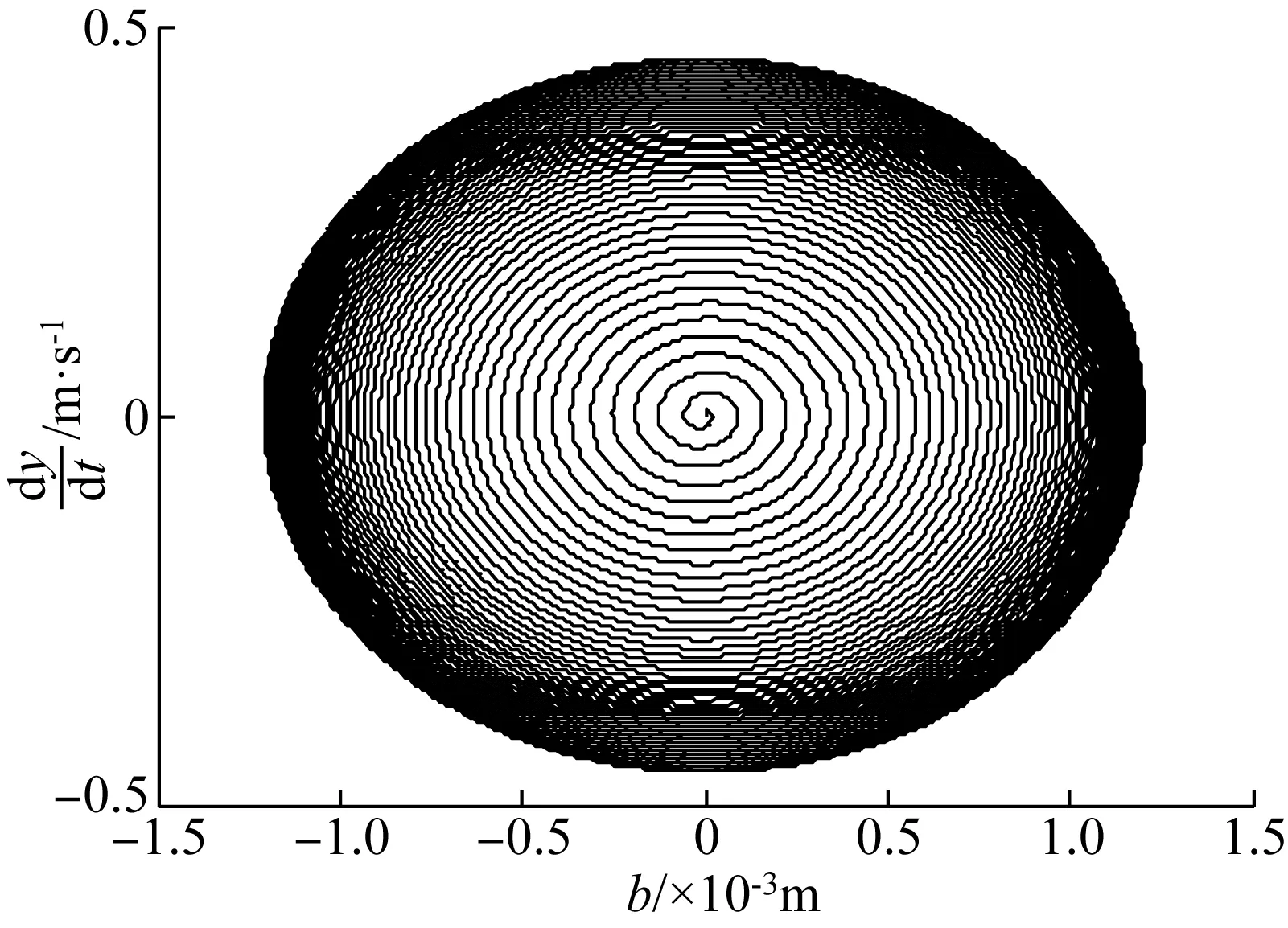
图4 非受控的相图Fig.4 Uncontrolled phase diagram

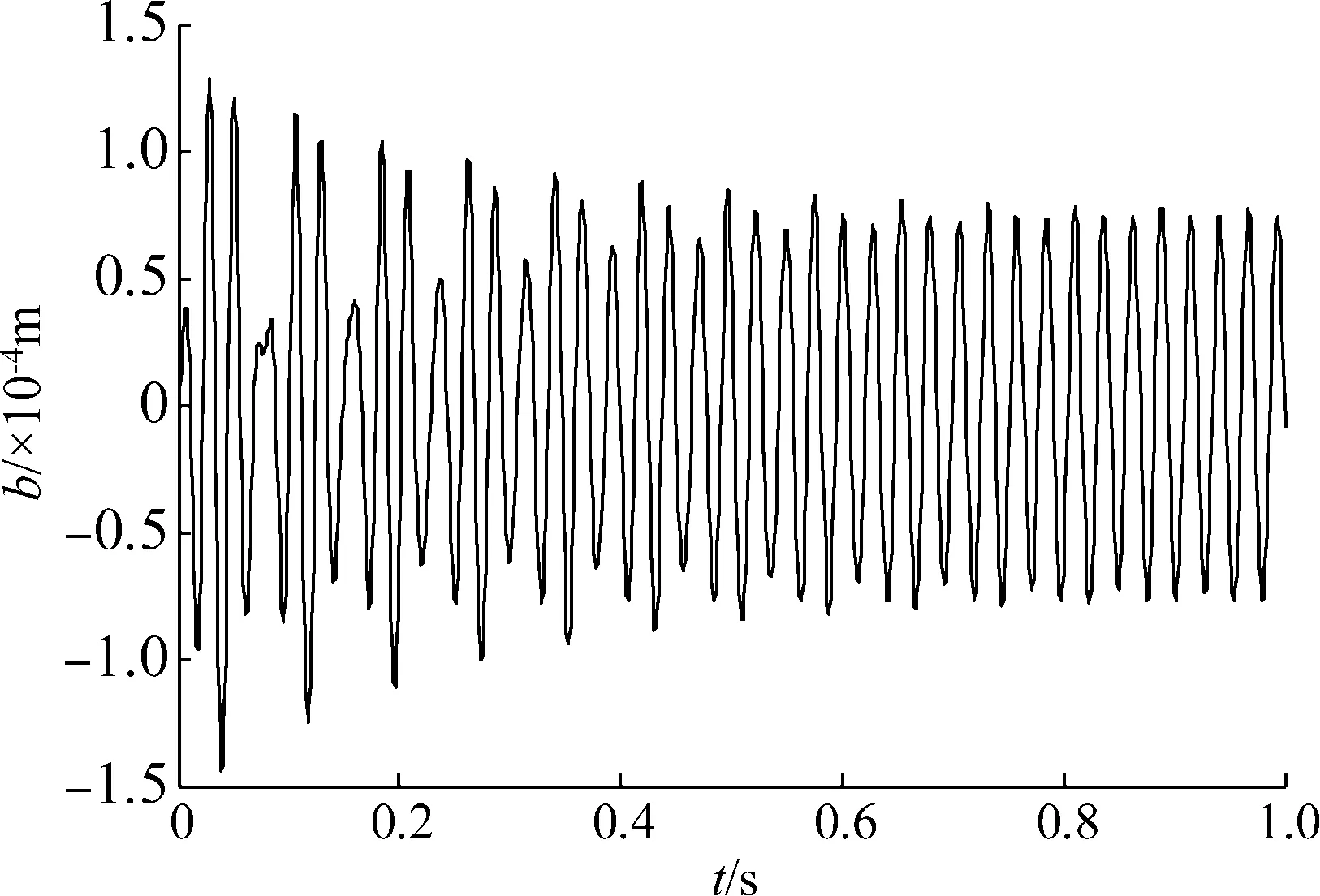
图5 工况1时域图Fig.5 Time domain diagram of case 1

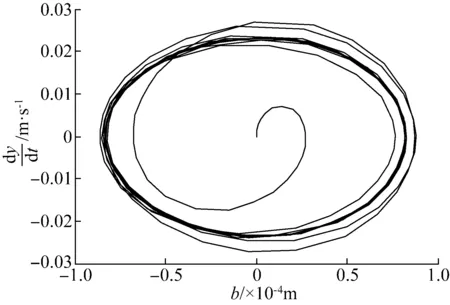
图6 工况1相图Fig.6 Phase diagram of case 1

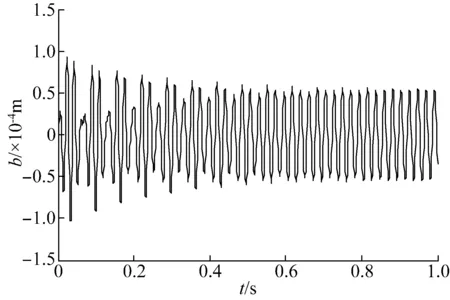
图7 工况2时域图Fig.7 Time domain diagram of case 2

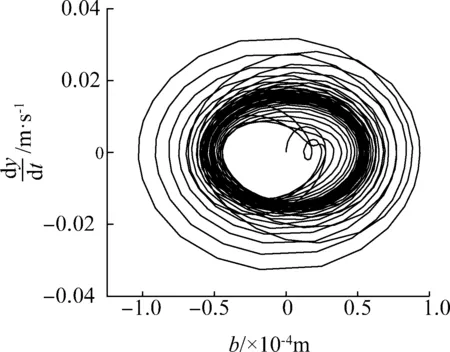
图8 工况2相图Fig.8 Phase diagram of case 2

从仿真结果的对比中可以看出,没有引入时滞反馈函数之前,带吸振器的轧机辊系主系统的振动幅值在起振瞬间缓慢的增大并最终达到稳定振荡。引入时滞反馈控制函数后,通过调整增益系数和时滞量,可以改善系统的振幅和收敛特性。当g1=10 000,g2=50,τ1=0.75T,τ2=0时,轧机辊系的振动幅值近似呈现等幅振荡的状态,系统的振动幅值相对减小并且极限环幅值趋于稳定。当g1=15 000,g2=50,τ1=0,τ2=0.75T时,轧机辊系的振动幅值出现收敛的情况并且极限环幅值很快达到稳定,同时轧机辊系的振动幅值进一步减小。

4 带吸振器的轧机辊系振动幅频特性稳定性分析

在轧机辊系的非线性动力学特性分析过程中,如果在幅频曲线中出现了幅值的“跳跃现象”,此时系统的振动幅值对应的出现一频多值的现象,不利于系统的稳定运行。为了避免轧机辊系振动幅频曲线出现跳跃现象,分别调整速度位移反馈增益系数和时滞量参数,消除轧机辊系振动幅值存在的多值振动。仿真结果如图9到图12所示。

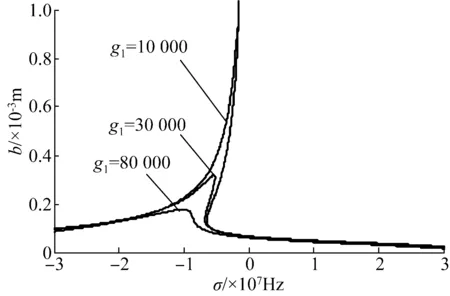
图9 随g1变化的幅频曲线Fig.9 Amplitude-frequency curves varying with g1

从图9到图12的仿真结果可以看出,随着反馈参数的变化,轧机辊系振动幅值的“跳跃现象”相应地出现一些不同程度的改变。

图9的仿真结果表明:随着位移反馈增益系数g1的增大,轧机辊系的振动幅值沿谷脊线减小,当g1的取值数量级大于 8×104时,轧机辊系振动幅值的“跳跃现象”逐渐消失。

图10的仿真结果表明:当g2的取值为200时,系统的“跳跃现象”消失;然而当g2在0到200之间取值时,轧机辊系的振动幅值减小,轧机辊系振动幅值出现“跳跃现象”的频率区段增大,系统的稳定性受到削弱。

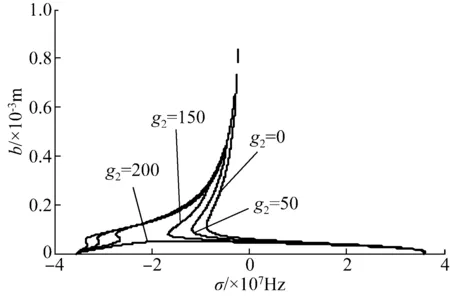
图10 随g2变化的幅频曲线Fig.10 Amplitude-frequency curves varying with g2

图11的仿真结果表明:时滞量参数τ1的变化不仅会改变轧机辊系振动的幅值,还会影响轧机辊系振动的固有频率以及“跳跃现象”出现的频率区间。

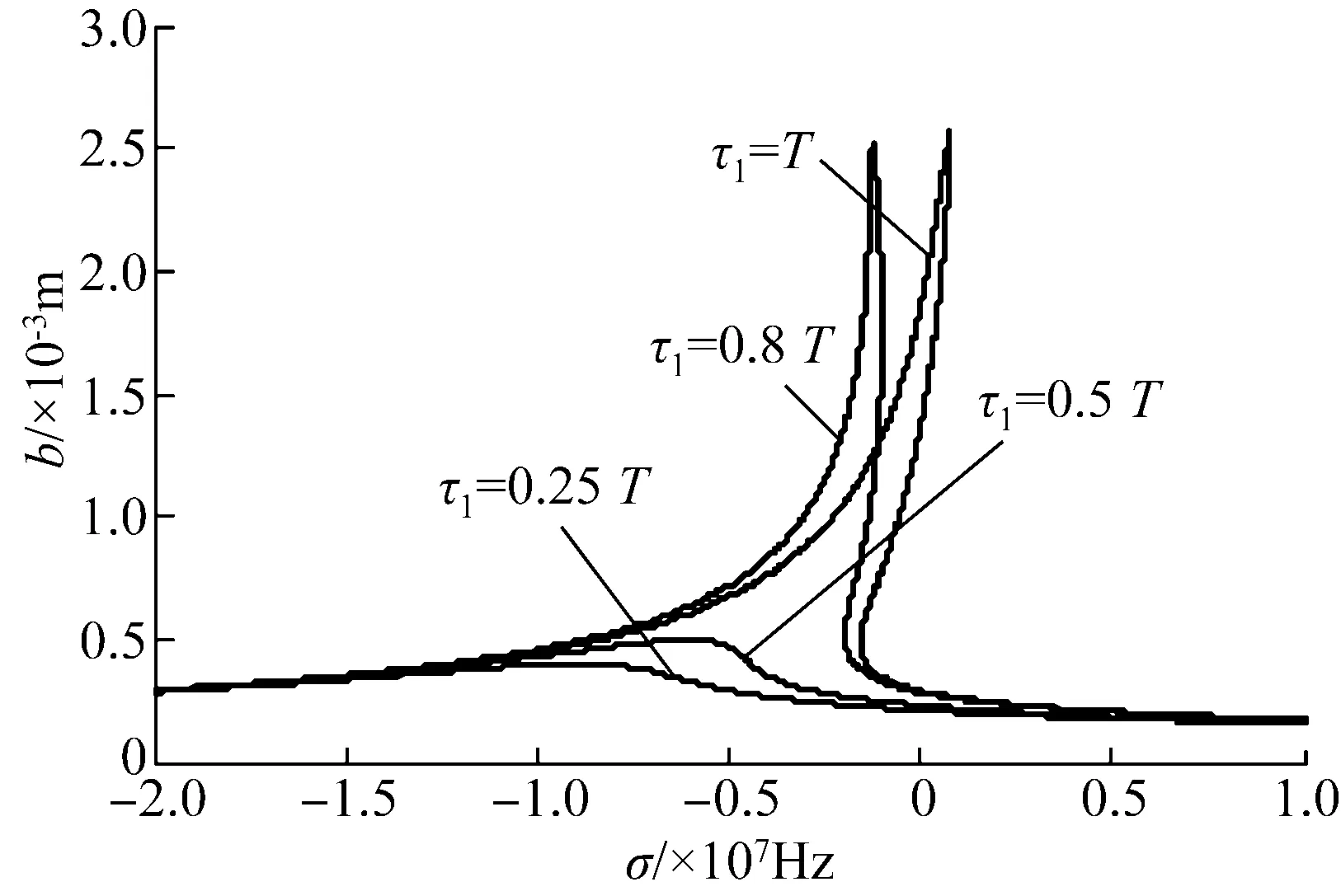
图11 随τ1变化的幅频曲线Fig.11 Amplitude-frequency curves varying with τ1

图12的仿真结果表明:相对于τ1的影响,时滞量参数τ2的变化没有改变轧机辊系振动的固有频率。随着τ2的变化,轧机辊系振动幅值沿着谷脊线变大或减小,当τ2=0.5T时,系统的“跳跃现象”消失,轧制系统恢复稳定。

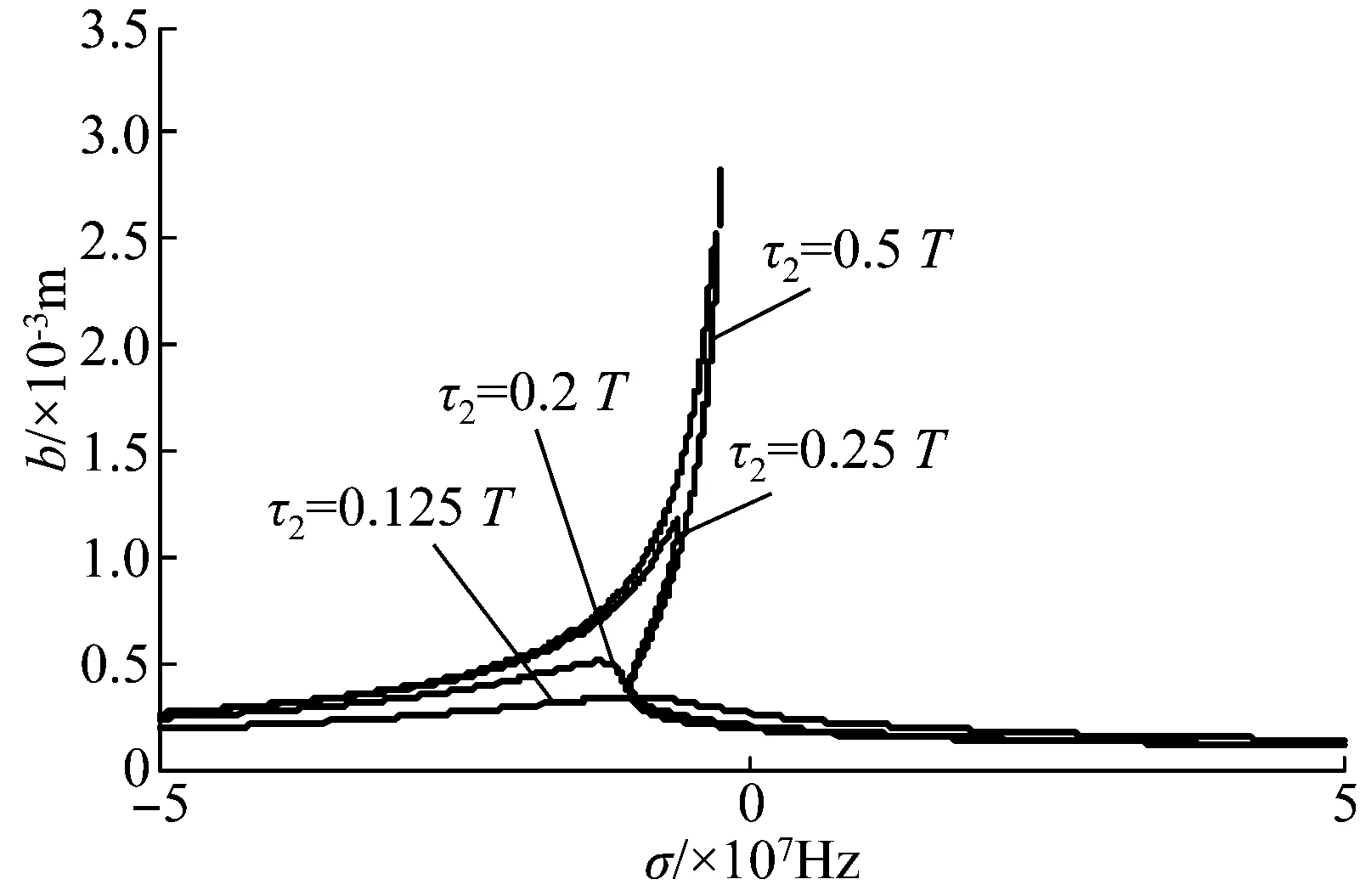
图12 随τ2变化的幅频曲线Fig.12 Amplitude-frequency curves varying with τ2

5 结 论

本文建立了一种带吸振器的轧机辊系振动模型,通过吸振器的弹性元件和阻尼元件将轧机辊系的振动能量转移到吸振器控制装置上,从而减小轧机辊系的振动位移,达到抑制振动的效果。引入时滞反馈控制函数,设计带吸振器的轧机辊系振动位移、振动速度的时滞反馈控制方程。采用多尺度法,求得轧机系统主共振和内共振情况下的幅频响应方程。分析了轧机辊系振动幅频特性的稳定性,得到不同反馈增益参数和时滞量参数对带吸振器的轧机辊系的影响规律,适当的增大反馈增益系数g1和g2,减小时滞量系数τ1和τ2可以改善系统稳定性和收敛性。