基于Adaboost算法结合DEGWO-SVM的财务困境预测
2022-01-04朱昶胜田慧星冯文芳
朱昶胜, 田慧星, 冯文芳
(1. 兰州理工大学 计算机与通信学院, 甘肃 兰州 730050; 2. 兰州理工大学 经济管理学院, 甘肃 兰州 730050)
由于世界各国的金融危机以及市场竞争日趋激烈,企业财务困境的预测引起金融机构的热切关注,建立一个准确、可靠的企业困境预警系统对于企业及时、有效地规避企业危机或破产风险有着极其重要的意义[1].金融领域大量的分析和实验表明,大部分企业破产都是由财务正常逐渐恶化,直到最后导致财务困境而破产,是一个动态发展的过程,是可以被有效预测的.我国证券市场将陷入财务困境的上市公司作特殊处理,定义其对应的股票为ST股[2].孙洁等[3]根据国家证监会的规定,将最近的两个会计年度的审计结果净利润率是否为负值(即一家上市公司持续两年亏损)作为该公司是否陷入困境的判断标准.本文对企业困境的界定同样以是否被ST为准,并采用上述的判断标准.
大量的模型和算法已被用于企业财务困境的预测研究.Fitzpatrick等[4]建立了单变量财务困境预测模型;Altman[5]提出了“ZETA”模型,以Z-SCORE作为判断企业困境的标准;Ohlson[6]运用了Logistic 算法并验证该模型在财务困境预测和分类的应用中有着不容小觑的作用;Sevim等[7]分析比较了Logistic、多元判断和单变量模型,实验得出Logistic在企业财务预警上有着更好的表现;Odom等[8]构建神经网络模型用来识别公司的财务风险状况,并取得了很好的预测效果;吴世农等[9]选用70家ST公司作为数据集,实验后发现,可利用财务指标来预测企业的财务状况;汤谷良等[10]提出基于大数据的财务困境预测模型;赵辰等[11]采用思维进化算法优化BP神经网络.
近年来,支持向量机(support vector machine, SVM)被广泛应用,并取得了良好的分类和预测效果.Shin等[12]利用SVM模型进行了企业财务困境预测,实验验证,该方法优于Logistic、神经网络模型.Jaekwon等[13]采用支持向量机与径向基函数结合进行研究,实验表明,该模型的预测性能优于神经网络模型.传统的SVM算法虽对小样本分类具有很强的泛化能力,然而,具有RBF核函数的SVM中有两个重要参数分别是惩罚系数c和核函数参数γ.惩罚系数c控制其模型复杂度和训练误差,核函数参数γ控制数据在向高维度投影后的缩放比例,影响模型的分类精度.一些研究表明,这两个参数对SVM的性能有着重要的影响,因此,在企业财务困境预测中这两个参数必须正确设置,才能保证预测模型的有效性.这两个参数在传统的SVM模型中是使用网格搜索方法寻优的,但其缺点是容易陷入局部最优.目前已有很多研究将元启发式算法(如粒子群算法、遗传算法以及人工蜂群算法等)运用在SVM参数寻优中,这些算法比网格搜索方法更有可能找寻到全局最优解.
灰狼优化算法(grey wolf optimizer,GWO)作为一种较新的元启发式算法,对SVM参数寻优也有着改进的潜能.Seyedali等[14]利用29个已知的测试函数,通过与PSO、GSA等五种优化算法进行对比研究,验证了GWO算法非常有竞争力.GWO具有较强的收敛性能、参数少、易实现等特点,但其存在收敛速度慢、优化精度低、容易陷入局部最优解的缺点,因此,本文将差分进化(difference evolutionary,DE)思想引入到GWO进行优化,以提高灰狼算法的全局探索能力,进一步提高对SVM参数的寻优能力.最早的Adaboost算法类型是由Freund和Schapire提出的一种用于二分类的Boosting集成学习方法.Adaboost算法具有调试参数少、不容易过拟合等优点,且Adaboost是一个框架,可以使用多种基学习器.Adaboost可将多个弱分类器有机地组合成强分类器[15],具有良好的提升分类准确率的能力.因此,本文采用Adaboost算法将DEGWO-SVM进行有机组合,以达到有效地提高分类准确率的目的.综上所述,本文旨在探讨并验证DEGWO解决SVM参数寻优以及Adaboost算法增强DEGWO-SVM的分类能力,并建立Adaboost-DEGWO-SVM组合模型,对78家ST公司和78家正常公司的数据集进行财务困境预测.
1 样本选取及预处理
1.1 样本选取
本文研究的样本数据来源于东方财务Choice金融终端,全部A股3 351家上市公司2015~2017年的财务数据.ST公司类用“-1”表示,正常公司类用“1”表示.同时,从现金流量、收益质量、盈利能力等类别中选取138个财务指标.
1.2 数据预处理
第一步,利用2015年和2016年的财务数据并以ST公司的判断标准,分析出2017年被ST处理的上市公司有78家.分析样本数据集,采用四分位图剔除异常值,并通过拉格朗日插值法补充缺失值.最后,选取78家正常公司与78家ST公司共同组成样本数据集.
第二步,通过皮尔森(Person)相关系数算法去除共线财务指标,初步得到一个36维的属性集.
第三步,利用主成分分析算法(PCA),设置累计贡献率为90%,筛选出13个重要财务指标作为建模属性.
第四步,数据归一化可让不同维度之间的财务数据在数值上有一定比较性,可以大大提高分类器的预测准确率,因此,每一维属性下所有数据都根据下面的公式归一化到区间[-1,1]:
(1)
式中:max和min分别代表属性中的最大值和最小值;a=-1;b=1.
2 算法分析
2.1 支持向量机
支持向量机(SVM)是目前较为主流的机器学习分类方法,由于其在小样本、非线性等方面存在优势并具有良好的预测表现,故实际应用非常广泛[16].
假设企业财务困境的样本集为:{xi,yi},yi∈(-1,1),其线性分类函数为
f(x)=ωx+b
(2)
yi[ωx+b-1]≥0 (i=1,2,…,n)
(3)
对最优的分类面的求解可转化为在式(3)条件约束下,求解式(4)函数的最小值:
(4)
导入拉格朗日乘子,即求解拉格朗日函数:
(5)
得到预测函数为
(6)
本文采用RBF作为SVM的核函数:
(7)
则最终将f(x)转化为
(8)
2.2 灰狼优化算法
Mirjalili等[17]提出的灰狼优化算法(GWO)是一种群智能优化算法,由于其具有较强的收敛性能、参数少、易实现等特点,近年来已被成功并广泛地应用到了参数优化、预测分类等领域中.该算法源于模仿自然界中狼群的狩猎过程,包括寻找、包围、攻击猎物等步骤.
1) 社会等级.灰狼社会等级分为4层,从高到低依次为α、β、δ和ω.每次迭代,由每代种群中的最好三个解α、β、δ来指导完成.α是最优解,β和δ是次优解,底层灰狼ω协助α、β和δ跟踪、包围、攻击猎物,以便找寻到最好的解决方案.
2) 寻找和包围猎物.灰狼在寻找、包围猎物时,灰狼与猎物的距离以及灰狼的位置更新公式如下:
(9)
式中:D表示灰狼个体与目标猎物的距离;A和C为系数向量;t为当前迭代的次数;X表示灰狼的位置;XP表示目标猎物的位置;a为距离控制参数,取值范围是[0,2];r1和r2为[0,1]中的随机向量.
每次的迭代过程,保存目前种群中最好的三只狼(α,β,δ),再根据它们的位置来更新其它狼群(包括ω)的位置:需要先预测猎物(潜在的最优解)的大致位置,其它候选灰狼再在目前最优α、β、δ三只狼的带领下,在猎物的附近展开搜索并更新其位置.候选灰狼的位置最终会处于α、β、δ所示的随机圆的位置内.
(10)
式中:Xα、Xβ、Xδ分别表示目前种群中α、β、δ的位置;Dα、Dβ、Dδ分别表示候选的灰狼与α、β、δ之间的距离.
图1是GWO算法的灰狼位置更新图.α、β、δ
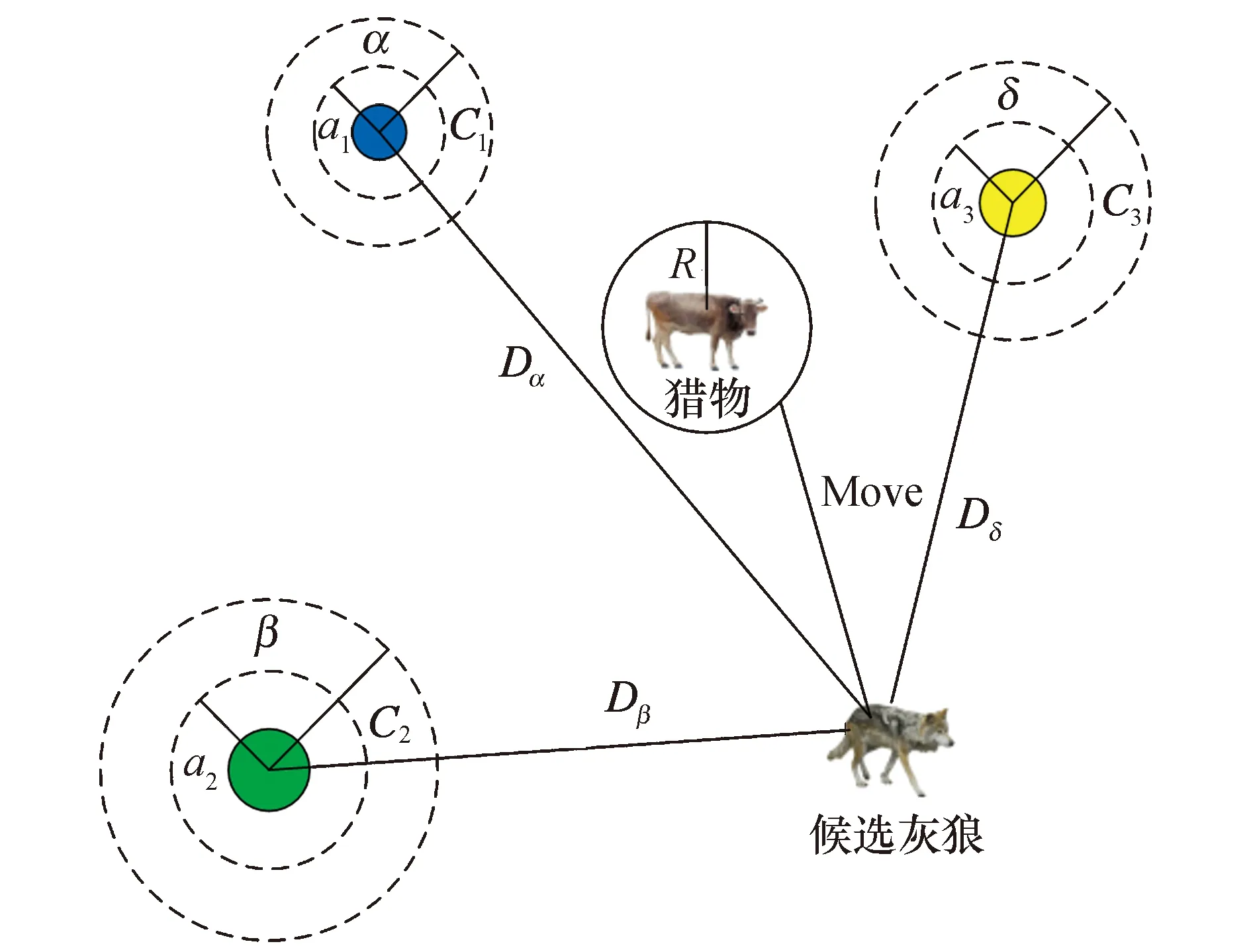
图1 灰狼优化算法位置更新图
3) 攻击猎物.当猎物停止移动时,灰狼通过攻击来结束捕猎.在迭代过程中,a值的减少会引起A的值也随之波动.当A>1时,灰狼分散在各区域搜寻猎物,即全局搜索寻优;当A<1时,灰狼集中在某些或某个区域内搜索猎物,即局部搜索寻优.
2.3 改进的灰狼优化算法
传统的灰狼算法收敛速度慢,优化精度低,且容易陷入局部最优.本文将差分进化思想(DE)引入到GWO进行优化,以提高灰狼算法的全局搜索能力.通过变异、交叉及选择三个步骤对狼群中的个体进化择优,引导搜索向最优解逼近.
1) 变异操作
求灰狼β、δ的向量差然后进行缩放,再与α狼合成,获得GWO变异因子:
(11)
式中:W是随机缩放因子,其取值范围为[0,2].在搜索初期,通过增大W提高GWO的全局搜索能力;在搜索后期,通过减小W提高GWO 算法的局部搜索能力.
2) 交叉操作
将狼群中经变异操作后产生的新个体与待变异的个体进行交叉产生中间个体.对于第i个个体的第j维,其公式为
(12)
其中:p表示交叉概率;rand表示[0,1]内的随机数.
3) 选择操作
经过变异和交叉产生的新个体与之前待变异的个体进行比较,计算每个个体的适应度,选择适应度好的个体作为新一代的狼群个体,其公式为
(13)
GWO算法改进后称为DEGWO.
算法1(DEGWO)的具体实现过程如下:
输入:nPop,MaxIt,nVar,pCR,lb,ub
(1) 初始化狼群位置;
(2) 计算每个灰狼个体的适应度,根据适应度值对狼群从大到小排序,依次为α狼、β狼、δ狼;
(3) fort=1 to MaxIt do
fori=1 tonPop do
forj=1 tonVar do
根据式(9,10)更新每个狼的位置
end for
end for
(4) fori=1 tonPop do
根据式(11~13)进行变异、交叉、选择操作
end for
(5) 计算每个灰狼个体在新位置上的适应度,更新α、β、δ狼的位置
end for
输出:α狼的位置(best_c,best_γ)
2.4 Adaboost算法
Adaboost是一种基于Boosting思想的提升算法,每次迭代后自适应地调整样本权重,分类错误的样本权重将增加,分类正确的样本权重将减少,每个弱分类训练结束后,加大分类误差小的弱分类器的权重,降低分类误差大的弱分类器的权重.
Adaboost算法实现过程如下:
1) 给定训练样本集:
T={(x1,y1),(x2,y2),…,(xN,yN)}
(14)
其中:i=1,…,N;yi∈{1,-1}.
初始化样本权重:
(15)
其中:N表示样本的个数;ωi表示每个样本的权重.
2) 进行迭代t=1,…,T.
选取一个当前误差率最低的弱分类器作为第t个基分类器Gt(x),并计算该弱分类器在Dt(i)上的分类错误率et:
(16)
计算该分类器在强分类器中所占的权重at:
(17)
更新样本权重:
(18)
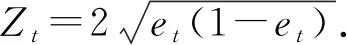
3) 将T个弱分类器按照各自权重at组合成一个强分类器:
(19)
3 Adaboost-DEGWO-SVM预测模型
本文提出Adaboost-DEGWO-SVM组合算法构建企业财务困境预测模型,集成了3种机器学习算法.Adaboost算法可将DEGWO-SVM作为弱分类器,有机地组成强分类器,有效提高分类准确率.
该算法流程可描述为:
Step1:导入企业财务困境建模数据集;
Step2:初始化样本的权重,设置弱分类器个数T为5,并开始迭代;
Step3:初始化DEGWO算法各参数,包括灰狼种群、最大迭代次数、交叉概率、参数下界和上界,以及灰狼个体的位置;
Step4:对全部灰狼个体进行遍历,计算出每个灰狼个体的适应度值,从大到小排序,依次为α狼、β狼、δ狼和ω狼群,采用分类准确率Accuracy作为该适应度函数;
Step5:根据式(9,10)进行全局寻优,更新a、A、C、D等参数值,更新狼群的位置;
Step6:根据式(11)进行变异操作产生变异中间体种群,通过式(12)进行交叉操作得到下个子代种群,计算子代个体的适应度值,再由式(13)进行选择操作,比较父代种群个体与子代种群个体的适应度值,选出更优的个体作为下一代种群;
Step7:计算每个灰狼个体在新位置上的适应度值,更新α狼、β狼、δ狼的位置;
Step8:判断,若达到最大迭代次数,循环退出,输出α狼的位置,即SVM的best_c和best_γ值;否则转到Step4继续运行;
Step9:采用步骤Step8的输出值进行SVM模型的训练和测试;
Step10:统计分类错误的样本数,设置弱分类器权重,更新样本集权重D;
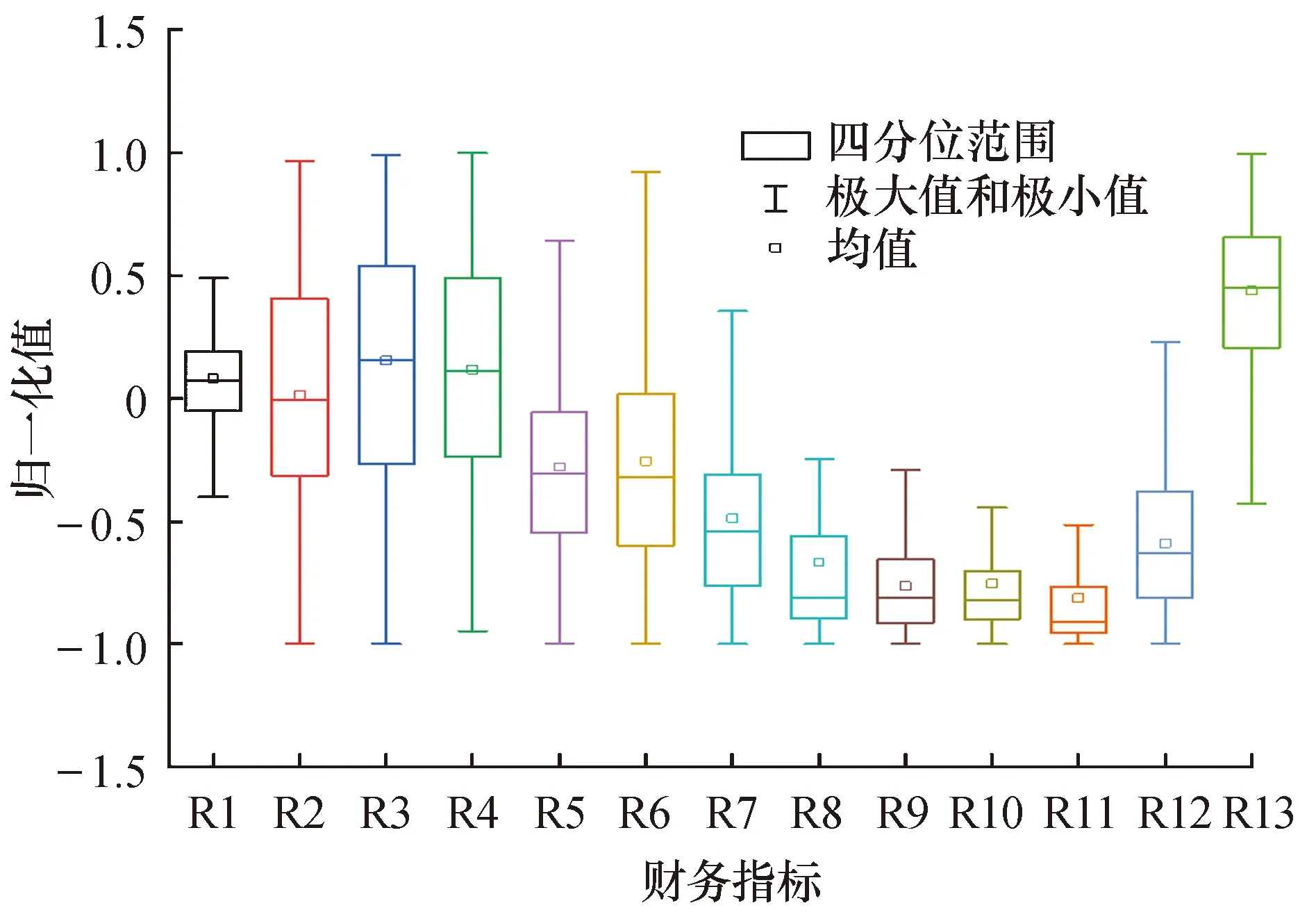
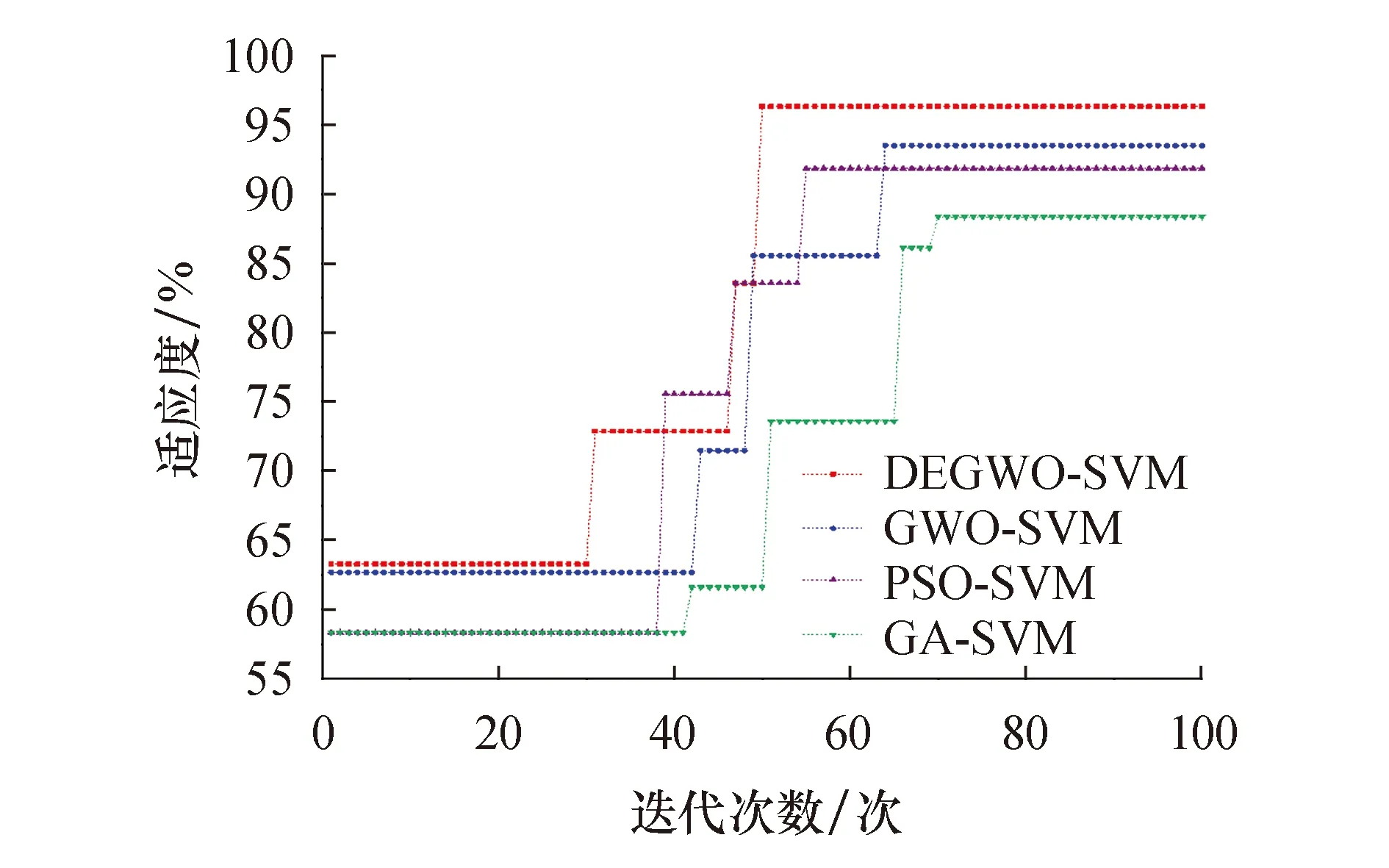
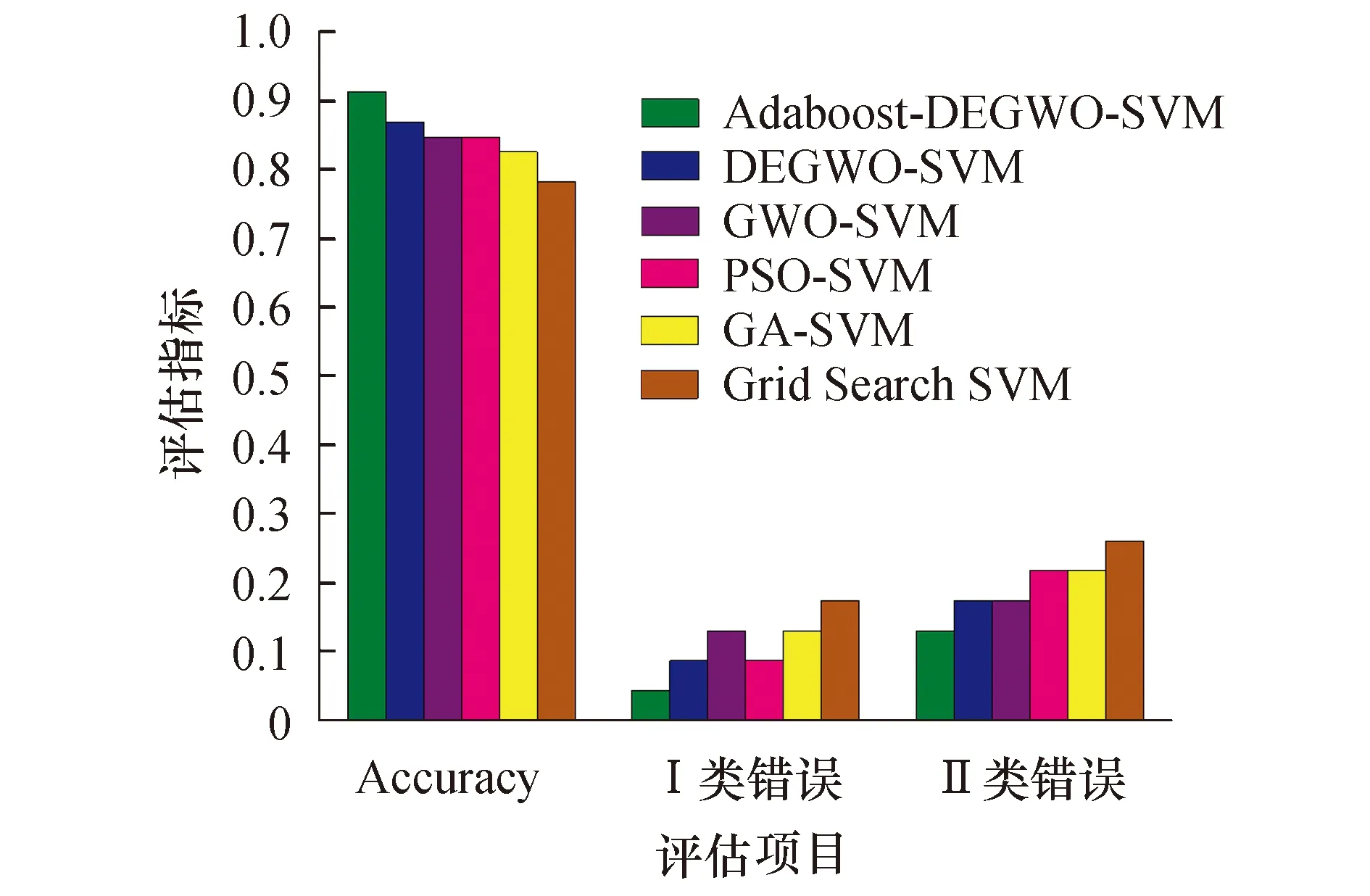
Step11:判断,若迭代次数t 图2为该预测模型的具体流程图. 图2 Adaboost-DEGWO-SVM流程图 本文在Windows 10 (64bit)操作系统的环境下,采用Matlab R2016b仿真软件,安装LIBSVM 3.24软件包进行实验.建模数据集共156组数据,属性指标13个,ST公司和正常公司的比例为1∶1,选取70%作为训练集,其余30%作为测试集. 本文采用分类准确率Accuracy、Ⅰ类错误、Ⅱ类错误作为算法的评估指标,定义如下: (20) (21) (22) 式中:TP是真正例,表示正常公司被正确分类的数量;TN是真负例,表示ST公司被正确分类的数量;FP是假正例,表示ST公司被分类为正常公司的数量;FN是假负例,表示正常公司被分类为ST公司的数量.Ⅰ类错误是指ST公司被分类为财务正常公司,Ⅱ类错误是指财务正常公司被分类为ST公司. 表1为经过数据预处理后选取的财务指标列表,包括财务指标名称及其计算公式. 表1 财务指标名称以及计算公式 图3是财务指标属性集归一化为-1到1范围后的每个属性的统计信息,包括极大值、极小值、均值、下四分位数(25%)和上四分位数(75%). 图3 属性集的数据特征 在Adaboost算法中,针对弱分类器个数的选取,分别尝试不同取值,每个取值分别做10次实验,可得强分类器的分类误差率在T=5时均值最小,因此,设置弱分类器的个数T为5.在DEGWO-SVM算法中,种群规模为50,最大迭代次数为100,自变量维数为2,缩放因子W∈[0.2,0.8],交叉概率为0.2,参数下界lb为0.01,上界ub为100. 本文选用Grid Search SVM、GA-SVM、PSO-SVM、GWO-SVM以及DEGWO-SVM作为对比算法.Grid Search SVM算法中,参数c和γ的选择采用网格搜索的方法,如c={2-2,2-1.5,2-1,…,24},γ={2-4,2-3.5,…,24}.GA-SVM算法中,最大进化代数为100,种群数量为50,参数c的取值范围为[0,100],参数γ的取值范围[0,1 000],交叉概率为0.7.PSO-SVM算法中,最大进化代数为100,种群数量为50,粒子维数为2,惯性权重因子为0.8,加速因子c1=1.6,c2=1.5.GWO-SVM算法中,种群规模为50,最大迭代次数为100,参数下界lb为0.01,上界ub为100. 在同一数据集上,采用网格搜索(GridSearch)、GA、PSO、GWO、DEGWO进行SVM的参数寻优,表2为各优化算法的参数寻优结果对比. 表2 各优化算法的寻优参数和性能对比 分析表2,SVM网格搜索方法耗费CPU时间最长,分类准确率也比GA、PSO、GWO及DEGWO都低,表明SVM网格搜索方法参数寻优能力较差.GA的参数寻优在CPU耗时及分类准确率方面与网格搜索方法相比都有进步.PSO与GWO的分类准确率都是84.78%,CPU时间相差不大,与GA和网格搜索方法相比,其CPU时间短且分类准确率有所提升.DEGWO的CPU时间为48.496 5 s,分类准确率可达到86.96%,是五种算法中参数寻优性能最好的.DEGWO与GWO相比,DEGWO所耗CPU时间减少了6.880 2 s,且分类准确率提高了2.18%,表明DEGWO有效地改进了GWO算法. 图4为GA、PSO、GWO、DEGWO优化SVM的适应度曲线对比图.经分析得出,GA算法在迭代到70次时开始收敛,适应度值为88.356 8%,与其他优化算法比较,其收敛速度最慢且收敛精度最低.PSO相对GA收敛速度较快,迭代到55次时收敛,迭代精度达到91.843 6%.GWO算法在迭代64次时收敛,适应度值达到93.489 8%,较GA和PSO算法收敛精度提高.DEGWO算法迭代到31次时精度开始提升,随后逐渐上升,迭代到50次时收敛,适应度值达到96.324 2%,与GWO比较而言,DEGWO算法收敛速度快,且收敛精度提高了2.834 4%.故DEGWO算法在优化SVM参数c和γ方面具有优势,同时也实现了对GWO的改进,解决了GWO收敛速度慢、优化精度低的问题. 图4 适应度曲线对比 为了验证本文所提模型的有效性,将本文所提算法与基于同一建模数据集上其他算法进行了比较.表3列出了本文所提算法与对比算法所产生的混淆矩阵的结果,包括46组测试数据分类后的详细情况.从表中可以看出,本文提出算法的分类准确率最高,可达到91.30%,其中只有1个ST公司被分类为正常公司,有3个正常公司被分类为ST公司.与本文所提算法相比,DEGWO-SVM、GWO-SVM、PSO-SVM、GA-SVM与GridSearch SVM在分类准确率方面较差,分别为2、3、2、3和4个ST公司被分类为正常公司,4、4、5、5和6个正常公司被分类为ST公司.实验表明,Adaboost-DEGWO-SVM算法在判别财务困境公司方面的能力优于其他算法. 表3 混淆矩阵 表4从分类准确率、Ⅰ类错误、Ⅱ类错误三个评估指标方面列出各算法的实验结果.Adaboost-DEGWO-SVM算法的分类准确率为0.913 0,Ⅰ类错误和Ⅱ类错误值分别为0.043 5和0.130 4,分类准确率最高,Ⅰ类错误和Ⅱ类错误值最小,表明本文提出的算法在财务困境分类应用中具备最佳的分类能力. 表4 评估指标对比 为了进一步直观比较各算法的分类结果,图5为各算法的评估指标对比图,包括分类准确率Accuracy、Ⅰ类错误、Ⅱ类错误.经分析得出,DEGWO-SVM比GWO-SVM分类准确率Accuracy提高了2.18%,且Ⅰ类错误降低了0.043 5,表明采用差分进化方法改进GWO有着较显著的效果.Adaboost-DEGWO-SVM算法与DEGWO-SVM相比,Adaboost-DEGWO-SVM的准确率Accuracy提高了4.34%,Ⅰ类错误、Ⅱ类错误分别降低了0.043 5;与单一SVM相比,分类准确率提高了13.04%,Ⅰ类错误、Ⅱ类错误分别降低了0.130 4、0.130 5,表明本文提出的算法在财务困境预测研究中是十分有效的. 图5 评估指标对比 本文构建了一种有效的组合方法Adaboost-DEGWO-SVM,准确地分类和预测了财务困境公司和正常公司.本文的创新点在于运用了新兴的群智能算法且协同3种机器学习算法构建组合模型,并利用DE改进GWO,通过探索DEGWO来优化SVM的参数选择,结合Adaboost算法最大程度地提高DEGWO-SVM的分类能力,以达到企业财务困境预测的目的.实验结果表明,本文所提模型在分类准确率、Ⅰ类错误、Ⅱ类错误方面优于其他五种模型.因此,可得出结论,Adaboost-DEGWO-SVM模型是一种潜在的企业财务困境预测模型,可为企业机构做出正确的决策提供帮助.
4 实验分析及对比
4.1 实验数据和评估指标
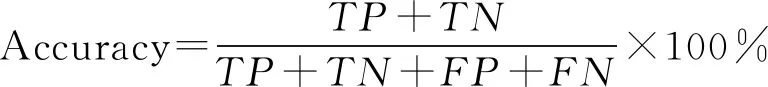

4.2 参数设计
4.3 实验结果及对比



5 结语
