知识本质解读视角下的数学课堂建构

刘小华

（晋安区教师进修学校，福建 福州 350005）

教师对知识本质的理解和把握是课堂建构的关键。从狭义上看，数学知识本质是指具体数学内容的本源意义。［1］它需要教师进入数学的具体内容进行挖掘，找到其背后的数学知识及其规律，了解其中蕴含的数学知识的本质属性和思想方法。数学知识本质是数学的灵魂，是数学教学的核心。小学数学课堂要关注和强调对数学知识本质的认识和理解，体现数学本身多角度多方位的影响。

一、把握本质，建构教学起点

知识学习是一个持续积累的过程。基于小学数学知识具有螺旋式上升的特点，教师在解读教材时，如能关注教材新旧知识之间的本质联系，在教学中便能够将学生的前后经验连接，建构教学起点，精准引导学生做指向明确的深入思考。

如在教学“小数的加减法”时，教师引导学生把握小数加减法的计算本质，进行深入的辨析与思考。

情境1：妈妈买了一件外套645 元，又买了一条裤子83 元，请问妈妈花了多少钱？

学生笔算得出645+83=728（元）

情境2：小明买了两本书，一本6.45 元，一本8.3元，小明花了多少钱？

学生中出现如下竖式：

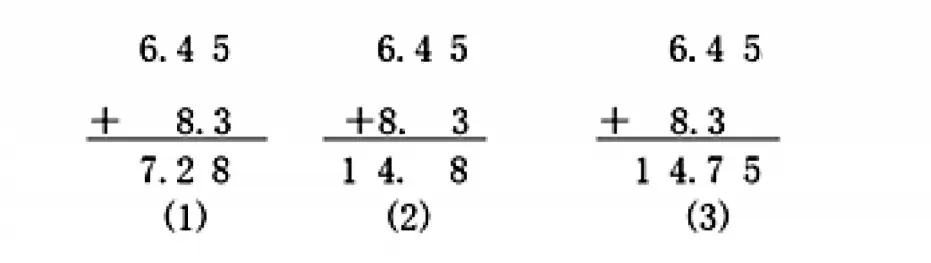
学生容易发现第一个竖式的错误，六元多加八元多不可能等于七元多，而对于第二个竖式产生疑惑：小数计算为什么不能像整数竖式那样末位对齐？由此聚焦小数加减法的本质，即对位值制的理解，并以此为起点展开教学。

在学习小数的加减法之前，学生已经具有丰富的整数加减法经验，但是通过前测，仍然发现很多学生把数位对齐浅层地理解为末位对齐。基于此，笔者深入研读教材，发现例题1（一位小数加减法）的教学无法让学生深刻理解小数点对齐的必要性。因此，大胆舍弃例题1，直接用例题2（一位小数加减两位小数）展开教学。因为对于大多数学生而言，没有合适的契机与前提，很难主动建构小数点对齐之“所以然”。教学中，教师合理引导学生暴露学情，从而产生学生原有认知系统与新知识之间的矛盾与冲突，引发学生在对比中主动思考：为什么小数加减法不能末位对齐？将学生的思维聚焦到第二个竖式，借助情境中“元、角、分”的单位载体、分数转化为整数、画图说理等多种办法，交流、辨析“3”表示3 个0.1，所以应该写在十分位，深刻理解“小数计算中小数点要对齐”的道理所在，即相同计数单位才能相加减，将位值原理内化，为学生自主建构提供良好的契机。

因此，教师要深入解读教材，不能就课备课，而要把握知识本质，思考加法是相同计数单位的累计，从一年级开始的整数加减、小数加减、分数加减等，无一不是如此。不但教授学生理解数学知识“是什么”，也教授学生洞察数学知识“为什么”，让学生感受其“源”和“流”。在此思想指导下，后一阶段的异分母分数加减法，小数乘除法的算理，会更加容易融会贯通。

二、厘清本质，建构思维阶梯

受思维方式、学习经历、生活经验的影响，学生的学习差异难免存在。但受教学现实条件制约，学生在学习相同主题时，必须要沿循相同的学习途径，抓住核心知识开展一系列学习活动。在这样的背景下，教师厘清知识本质，建构由简单到复杂、相互关联的学习阶梯，以满足全体学生的思维发展的需要，显得尤为重要。

例如，“长方形的面积”的学习，作为平面图形面积计算的起步课程，决定着学生对其他相同主题的后续学习。教学中应思考：其公式由来及教学意义何在？平面图形的面积计算为什么要从长方形开始，其教学阶梯如何搭建？［2］基于此，教师深度研读教材，厘清了面积计算的本质是度量，长方形的面积即是长方形中包含单位面积数的总和，即具有“可加性”。教学时，出示以下两张门票：

学生探究上述门票（图1）的面积，暴露出三个思维层面：1.画满格子；2.做记号平移格子，列出算式6×3；3.直接列算式。教师带领学生开展说理过程：“为什么要画格子？为什么他不画格子也知道面积是18cm²？他只用了算式6×3 表示，谁看懂了？”而对于没有格子的门票（图2）的面积，学生同样暴露出三个思维层面：1.画满格子（但是人数不多）；2.只画行、列各一排格子；3.直接写算式。学生思考的是：“他画的是多大的格子？为什么不画格子也知道面积是35cm²？他用了算式7×5 表示，谁看得懂了？”

图1

从以上教学实践可见，对于教材，除了整体把握，还要有深度的解读。对于一个知识点，力求用一个问题串来解决，并争取扩展为一个知识链，保证学习途径的连贯与递进。教师以格子为载体，在同一学习途径中，力求让不同思维层次的学生进行有差异性的探究，从画满格子到画行、列各一排再递进到直接计算，拾级而上，逐步完成长方形面积计算中行、列格子数与长、宽对应关系的探究活动。在步步推进的过程中，学生理解长方形面积为什么是“长乘宽”，感悟到平面图形面积的本质是“数”，可逐个数，也可逐行数，由“数”升华到“乘”，得到“数”的经验，产生“算”的需求。从直观到抽象，从数到算，思维差异慢慢得到弥补，有效建构螺旋上升的数学思维阶梯。［2］

三、凸显本质，建构知识体系

郑毓信教授说过：基础知识不应求全，而应求“联”。求“联”即将相关的知识建构成一定的知识体系，而牵动此“联”的脉络无非是知识的本质属性。应清晰了解知识体系编排的逻辑性，了解其螺旋式上升的特点，将每一节课的教学内容放到横向和纵向体系中认识和理解，引导学生知道其内在联系，找到知识的本质属性，建立知识的坐标轴，向相关的知识进行延伸和拓展，形成体系。

以“三位数乘两位数”为例，这是小学阶段整数乘法的最后一个学习内容，其中蕴含的算理算法可进行迁移。因此，本节课应该思考的是作为笔算终结课，该如何进一步凸显整数乘法的计算本质，以系统化知识结构，进一步提升学生的数学素养。基于此，教师在学生板演“145×12”的竖式后，着力把握知识脉络节点，沟通新旧数学知识和方法之间的联系，组织讨论：“今天的算式发生了什么变化？没有教，怎么都会？”“三位数乘两位数与两位数乘两位数有何不同？怎么解决？”两个问题的引导，成功搭建对“三位数乘两位数”的笔算方法的认知平台，并将竖式形式上的类推提升到对算理的内化。学生初步感受到数学知识的系统性，数学思维发展更上一层楼。［3］

作为课堂教学的主导者，教师在解读教材时，应努力尝试对教学内容进行系统化、条理化的归纳，力求让知识结构多元和关联。本课结尾，教师再次带领学生总结、回顾、反思乘法计算的算理、算法。

师：通过今天的学习，能够类推出什么？

生：四位数乘两位数，五位数乘两位数……

师：如果第二个因数也是三位数呢？

生：（）位数乘三位数。

师：如果两个因数都是多位数，我们的课题可以怎么写？

生：（）位数乘（）位数。

这三个问题，使学生再次沟通知识的内在本质联系，实现算理算法的和谐统一，进一步理解运算过程中的位值原则与运算律（乘法分配律）这一计算的本质所在，整数乘法的知识体系得以建构。本节课为小学阶段的整数乘法做了一个完美的收尾，也为下一阶段的小数乘法做好铺垫。［3］