在比较中实现概念的深度学习——以“周长”和“面积”的概念学习为例

宋晓春

（同安区第三实验小学，福建 厦门 361100）

马云鹏教授认为，深度学习是一种基于理解的学习，是学生以高阶思维的发展和实际问题的解决为目标，以整合的知识为内容，积极主动地、批判性地学习新知识和思想，并将它们融入原有的认知结构中，且能将已有知识迁移到新的情境中的一种学习。［1］小学数学教学中实现概念的深度学习，应着力引导学生经历概念的形成过程，促进学生对概念的本质理解，实现概念的灵活应用，并能将新概念纳入原有的概念结构。比较可以帮助人们把握事物的异同点，区别事物，达到对各个事物的深入了解认识，从而把握各个事物。

在小学数学概念教学中，“周长”和“面积”是跟平面图形有关的两个概念，分别安排在人教版三年级上下册中。学生在三年级下册学习面积相关知识后，对于周长和面积这两个概念总是很容易混淆。为了帮助学生更加准确、深刻地理解这两个概念，在学完“面积”这一单元后，教师应有意识地引导学生对“周长”和“面积”的含义及其计算方法进行比较分析。在不同概念异同点的对比中，开展深层次对话，实现概念的深度学习。

一、比较“线”与“面”，经历概念形成

数学概念具有抽象性，而小学生的思维特点是以具体形象思维为主，具体形象思维逐步向抽象逻辑思维过渡。纯粹的机械记忆并不能让学生真正理解概念，只有经历概念的形成过程，积累认知体验，学生对概念才能获得真正意义上的生动的理解。教材中对周长的定义是“封闭图形一周的长度”，对面积的定义是“封闭图形或物体表面的大小是面积”。比较“周长”和“面积”这两个概念的形成过程，可以发现“周长”计量的对象是“线”，而“面积”计量的对象是“面”。所以在概念教学中，首先要让学生感悟到“线”与“面”的不同，从而意识到“周长”与“面积”的不同。

1.动态感知，展示特征

小学生的思维以直观思维为主，动态地展现概念，有利于学生获得直观体验，印象更深刻。如用课件展示一个长方形，请学生上台比一比，说说长方形周长指的是什么？面积指的是什么？课件先呈现红色线绕长方形一圈，并且将这一圈展开，里面包含两条长和两条宽的过程，由此直观呈现“长方形的周长就是长方形一周的长度，也就是2 条长和2 条宽的长度总和”这一概念。接着，呈现“蓝色涂满整个长方形”的过程，引领学生直观感受，蓝色部分就是这个长方形的面积。动态展示，让学生对“线”与“面”的特征感受更加强烈。

2.操作体验，亲历实践

设计操作性的实践练习，让学生在动手中直观体验“线”与“面”和不同。如设计“摸一摸、说一说、找一找”的操作活动，让学生在多种操作中，直观感知周长和面积的不同，形成表象。或请学生先用红笔描出以下每个图形的一周，再涂蓝色，表示出它们的面积（见图1）。在“涂一涂”的活动中，在“红线”与“蓝块”的视觉对比冲击中，强化“线”与“面”的不同。

图1

3.观察对比，深化认知

设计两个图形的比较“周长”与比较“面积”的练习，让学生在观察对比中，不断深化“周长计量线、面积计量面”的认知。如请学生比较甲、乙两个图形，谁的周长更长？谁的面积更大？学生观察发现，图2 中，甲乙两个图形其实都包含两条长和两条宽，周长一样长；但甲面积小，因为它缺了一小块。图3 中，两个图形都是由两条直角边和一条曲线围成，直角边和曲线的长度相等，所以周长相等。但是曲线围绕直角边的方式不同，可以直观看出乙的面积更大。

图2

图3

二、比较“计量标准”，把握概念本质

概念的学习，不能仅仅停留“表面理解”“浅层理解”，而要实现“深度认知”“深层理解”。这就需要教师把握概念的本质。张奠宙教授说：“许多数学本质，只有从历史的发展（中）才能深刻体会。”教师要溯本求源，追问概念的前世今生，重视知识的来龙去脉，在历史的脉络中寻求概念的本质。测量图形的周长，测量的是“线”的长短；而“线”的长短，就是二年级时学过的线段的度量，就是一条线段里包含几个“单位长度”。测量图形的面积，测量的是“面”的大小，也就是一个“面”里包含几个“单位面积”。周长和面积本质是相同的，都是“度量”，也就是要先确定度量的标准单位，再算算图形中包含几个这样的标准单位。［2］测量周长使用的标准单位是“单位长度的线段”，测量面积使用的标准单位是“单位面积的小正方形”。

1.数一数，化形为数

教师引导学生加强“数一数”的练习，巧妙地化“形”为“数”，让学生深刻领悟“周长”和“面积”的本质——“数一数有几个标准单位”。同时，通过数“线段”还是数“小方格”，感悟“计量标准”的不同，进一步明晰“周长”和“面积”的不同。

如图4，比较面积，应该数“小方格”。甲有10 个小方格，乙也有10 个小方格。学生在数格子中发现，甲乙形状不同，但是面积一样。比较周长，应该数“线段”（小方格的边）。甲一周有14 段，乙一周有16 段，所以乙周长比较长。

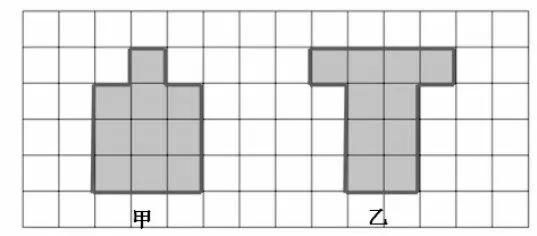
图4

2.画一画，逆向思考

教师引导学生在方格纸上“画一画”，在“画”的过程中，对比周长与面积在计量标准上的不同。设计教学活动如下：

（1）在方格纸上画几个长方形或正方形，使它们的周长都是12 厘米。（每个方格的边长表示1 厘米）

（2）在方格纸上画几个长方形或正方形，使它们的面积都是12 平方厘米。（每个方格的边长表示1厘米）

“画一画”比“数一数”难度有提升，蕴含着逆向思考的过程。面积是12 平方厘米，意味着画的图形里要包含12 个小方格，所以每排的个数（长）乘几排（宽）要等于12；周长12 厘米，意味着图形一圈的长度是12厘米，即“长+长+宽+宽＝12 厘米”，也就是“（长+宽）×2＝12”，所以长+宽＝6。学生在“画一画”的过程中，对周长和面积的本质进一步辨析理解，对长方形、正方形的面积公式进行逆运用，思维含量较高。会“画”，说明学生对周长和面积的计量单位已经具有清晰的认识。

三、比较“问题情境”，落实概念应用

概念的深度学习，一个重要表现在于能够正确、灵活地运用概念。因此，在概念教学后，教师应该把概念融合到数学问题中，引导学生积极地在比较分析中解决问题，进一步明晰概念、理解概念，实现概念应用。教师可以设计多种关于“周长”与“面积”的实际问题情境，引导学生比较分析，明晰概念，提升应用数学概念解决数学问题的能力。

1.设计具体情境

教师提供一些现实生活中的情境，让学生根据对概念的理解，直接判断是周长问题还是面积问题。如请学生想一想，以下情境，是跟周长有关，还是跟面积有关？①体育课上，同学们沿着操场的周边跑了2 圈。②工人叔叔粉刷房间的墙壁；③放学后，值日生把教室全部打扫一遍；④给草地围上围栏。学生在比较生活中应用周长和面积的情境中，生动理解周长和面积。

2.设计对比情境

教师直接呈现包含“周长”问题和“面积”问题的题组，让学生在同一题组中进行对比辨析。如三年级下册练习十三的第6 题：“墙报的面积是多少平方分米？花边的总长是多少分米？”同一题里有“周长问题”，也有“面积问题”，学生必须先对比做出判断后，才能选择对应的公式进行计算。

3.设计隐含情境

有些题目没有出现“周长”或“面积”的字眼，学生需要结合自己的生活经验判断，进一步促进概念的理解。如三年级下册练习十三的第8 题：“洒水车每分钟行驶200 米，洒水的宽度是8 米。洒水车行驶6 分钟，能给多大的地面洒上水？”学生联系洒水车洒水的场景，明白求多大的地面，相当于求洒水地面的面积，洒水车行驶的路程相当于洒水地面的长，洒水宽度相当于洒水地面的宽，所以运用长方形的面积公式进行计算。

四、比较“变与不变”，沟通概念关联

数学中每个概念的学习，呈点状结构，相对是零散的。但教师不能孤立地看待每个概念，而应站在整体的高度，寻找并沟通各个概念之间的关联，引导学生在系统和结构中认识概念，促使学生形成概念网络，完善概念的认知结构。

1.联系的视角

比如，正方形的边长、周长、面积三者之间，知道其中一个量，就可以推算出其他两个。教师设计练习：“一根16 分米的铁丝围成一个正方形，这个正方形的面积是多少平方分米？”学生需要分析，16 分米是铁丝的长度，也是这个正方形的周长，知道正方形的周长，就可以推出正方形的边长，进而算出正方形的面积。通过沟通边长、周长、面积三者之间的关联，使学生对边长、周长、面积等概念的认识更加清晰。

2.变化的视角

“周长”和“面积”两个单元，教材特别重视从“变化”的视角引领学生探究周长与面积的关联。如三年级下册练习十四第65 页第七小题“在方格纸上画几个长方形或正方形，使它们的周长都相等，然后比较一下它们的面积。你能发现什么？”练习十六第75 页的第11 题“在方格纸上画出面积是16 平方厘米的长方形，你能画几个？算出它们的周长，填入表中。”两道题目实质上是聚焦“变”与“不变”的两个问题探究：一是周长相等的图形，面积一定相等吗？二是面积相等的图形，周长一定相等吗？［3］

两道题目编排分散，不利于学生整体上比较把握“周长”与“面积”的变化特点。因此，有必要安排专门的一课时，组织学生针对这两个问题，同时开展对比性探究，并及时归纳、小结其中的规律。针对前述第一个问题，教师可提供学习单（见图5），引导学生探究。学生自主思考，画一画、算一算、填一填，完成学习单，在观察、思考中发现：“周长相等的长方形，它们面积不一定相等；周长相等时，长和宽越接近，面积就越大。”针对前述第二个问题，教师也提供给学生类似的学习单并组织学生开展类似的研究。两个研究完成后，再组织学生对比感悟“变与不变”的辩证关系。

图5

这样专门设计的聚焦“变”与“不变”的课，进一步关联了“周长”和“面积”的变化关系，促进学生深层次理解，为后续学习积累更多有价值的经验。