自平衡独轮滑板车的动力学分析

刘延柱

(上海交通大学工程力学系，上海 200240)

自2008 年北京奥运会上自平衡的赛格威车首次亮相以来[1]，2015 年出现了赛格威车缩小版的自平衡双轮滑板车[2]。与此同时，又有构造更简单的称为“Onewheel” 的自平衡独轮滑板车问世(图1)[3]。这种新型的代步工具只有一个轮子，仅依靠驾车人的身体动作就能实现加速、减速和转弯等各种功能。虽然操纵难度比双轮滑板车更大，需要掌握更多技巧才能熟练驾驶，但骑手能感受到自由飞翔般地飘浮感觉，因而备受年轻人的青睐。各种新设计和产品不断涌现，促使自平衡滑板车的技术和产业在国内快速发展。

图1 自平衡独轮滑板车和骑手

自平衡滑板车的出现为力学科普提供了一个有趣的课题。重心高高在上的骑手如同一只倒置的复摆，稳定的自平衡是如何实现的？根据经典力学的基本原理，任何系统的运动状态只能依靠外力的作用改变。自平衡滑板车仅靠驾车人扭动身体就能改变运动状态应如何解释？独轮车与地面只有一个点接触，约束力不能形成绕垂直轴的力矩，转弯的动力从何而来？就上述问题本文讨论自平衡独轮滑板车的动力学原理。忽略骑手肢体动作引起的质量变化，将车架加骑手视为刚体，与车轮组成双刚体系统。设车轮相对地面做纯滚动，滑板车的运动被归结为非完整约束条件下双刚体系统的动力学问题。

自平衡独轮滑板车的构造十分简单。在钢制框架的中心用轴承安装一只粗壮的橡胶轮，前后各装有一片木踏板(图2)。骑手跨立在车轮前后两侧，通过重心移动改变足底对前板或后板的压力。板内安装的加速度计将测出的信息通过控制系统传输至驱动电机，以控制车轮的加速或减速。

图2 自平衡独轮滑板车

需要转弯时，与驾驭滑雪板或冲浪板的方法类似，驾车人带动车体向要转弯的一侧倾斜。利用与自行车类似的“离心力效应”和“陀螺效应”，倾斜车体的重力与支承力构成力偶，使旋转中的车轮进动，出现绕垂直轴的转动。由此产生的陀螺力矩与重力矩平衡[4]。车体绕垂直轴的转动使直线轨道发生偏转，从而实现转弯动作。沿曲线轨道行进的车体和人体产生离心惯性力，使驾车人恢复直立姿态避免摔倒。独轮滑板车厚重车轮的动量矩明显大于自行车的前轮，陀螺效应也更为明显。

将车架和固定在车架上的骑手作为刚体B0，车轮作为刚体B1。独轮滑板车是由B0和B1以圆柱铰连接组成的双刚体系统{B}(图3)，其中，R为车轮半径，B1与地面的接触点记为P。将车轮不转时{B}固结成的刚体记作B*。以B*的质心Oc为原点，建立平动参考坐标系(Oc-XY Z)，X和Y轴与地面平行，Z轴为垂直轴。设(Oc-XY Z)绕垂直轴转过φ角的位置为(Oc-x0y0z0)，x0轴为车轮的前进方向。继续绕x0轴转过ψ角为(Oc-x1y1z1)，y1轴为车轮的旋转轴。最终(Oc-x1y1z1) 绕y1轴转过θ角为刚体B*的主轴坐标系(Oc-xyz)，z轴沿骑手身体的纵轴(图4)。

图3 双刚体系统

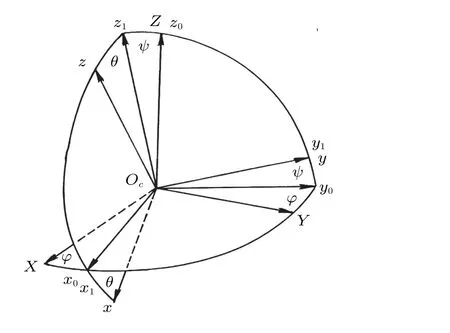
图4 参考坐标系

以骑手在车板上直立，滑板车匀速直线前行作为稳态运动。即φ=θ=ψ=0，Ω=Ω0，质心速度vcx=RΩ0，vcy= 0。其中Ω为转速，Ω0为稳态转速。骑手利用身体向前或向后的倾斜动作控制车速。当骑手向前倾斜时，因重力对前板的压力大于后板，使车板产生角加速度¨θ。安装在车板内的加速度计将测出的¨θ信息输入控制系统，积分后转换为转角θ和角速度˙θ信息，控制驱动力矩使车轮加速。如向后倾斜则控制力矩方向相反，车轮减速。即使在稳态行进过程中，若骑手因扰动向前倾斜，车体会自动加速，产生向后的惯性力使骑手恢复原位。向后倾斜则减速产生向前的惯性力。因此这种速度控制系统也是骑手站立稳定性的根本保证。

仅保留小量φ，θ，ψ及其导数的一次项，设i，j，k为x，y，z各轴的基矢量，B*的角速度为ω= ˙ψi+ ˙θj+ ˙φk。设B1相对B*的旋转速度为Ω=Ωj，从B1的质心即轮心O至B*的质心Oc引矢径l=lk，从B1与地面的接触点P至轮心O引矢径R=Rk(图3)。设Oc的速度为vc=vcxi+vcyj+vczk，则P点的速度为vP=vc+(R+l)×ω+R×Ω，导出

将参考坐标系的原点Oc移至轮心O，设{B}的质量为m，以(O-xyz)为参考坐标系，列写{B}在重力mg和约束力F作用下的质心运动方程

将式(8) 中的F以式(5) 代入，向(Oc-xyz) 各轴投影，得到

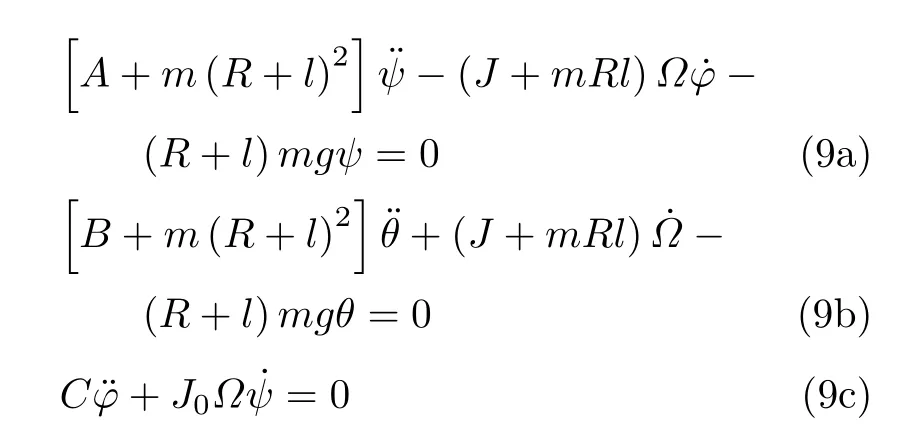
若不加控制，令式(9b) 中 ˙Ω= 0，则成为倒置的复摆方程，θ=0 为不稳定的直立状态。若施加控制，采用与θ成比例的最简单的控制方案

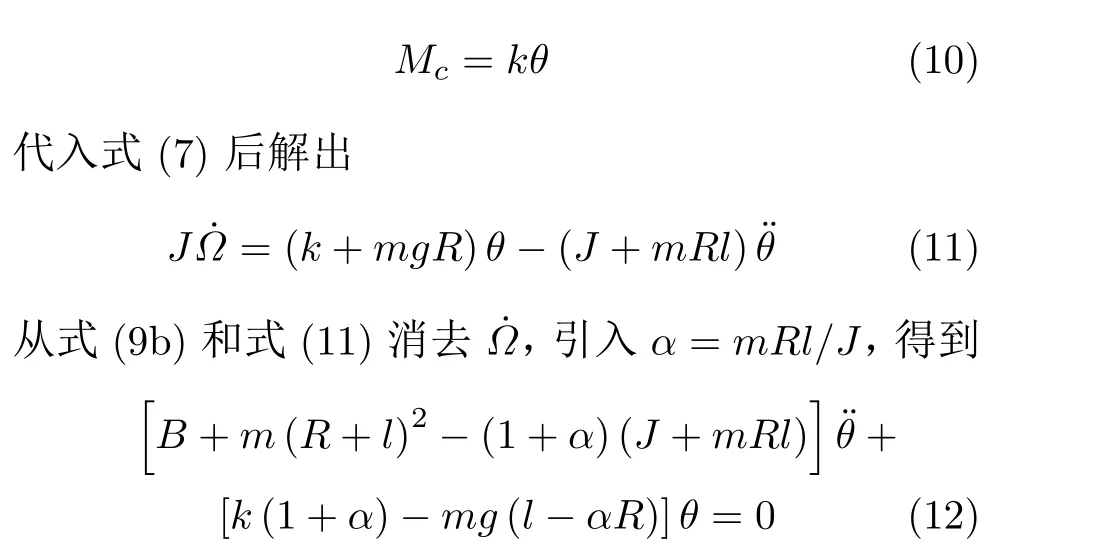
将车轮视为均质圆盘，令J0=m1R2/2，则J=m*R2，m*=m+(m1/2)，引入α=ml/(m*R)。将式(12) 中¨θ的系数中带负号部分化作

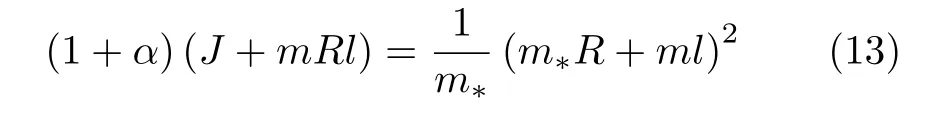
因m ＞＞m1，m*与m接近，若将式(13) 右项的分子和分母中的m*均以m近似代替，则化作m(R+l)2。可推知式(12) 中¨θ的系数近似等于B。方程(12) 的特征方程为

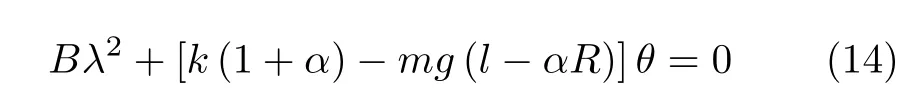
若令控制系数k满足

则特征根为纯虚数，θ=0 为稳定平衡，证明骑手的直立状态对前后侧扰动保持稳定。但根据运动稳定性的一次近似理论，线性系统的特征根实部为零属于临界情形，只能判定线性系统的零解稳定，而不能判断未经线性化的原系统的稳定性[5]。

为提高控制过程的灵敏性和稳定性，可在简单控制规律(10) 中增加随˙θ变化的因素，变为

则方程(12) 中应增加一项k1(1+α) ˙θ，特征方程变为

因特征根的实部均为负数，根据李雅普诺夫一次近似稳定性理论，此线性系统的零解变为渐近稳定，且能判定原系统的零解亦渐近稳定。

对滑板车变向和转弯的解释须利用方程 (9a)和(9c)。设车轮转速在转弯过程中维持常值Ω0不变。当骑手开始向右侧倾斜时，尚未变向的车体仍维持短暂的 ˙φ=0。方程(9a) 成为以ψ为变量的倒置复摆的动力学方程。重力导致的倾覆角加速度 ¨ψ从零开始按指数规律增长。当增长至有角速度 ˙ψ出现时，引起车轮的动量矩矢量L1进动，产生陀螺力矩JΩ0˙ψ。依据方程(9c)，车体出现绕z轴的角加速度¨φ，使前进方向发生改变趋势。所产生的惯性力矩C¨φ与车轮的陀螺力矩平衡。当角加速度¨φ随时间积累到有φ角出现时，转弯过程完成，直线运动变为曲线运动。所产生的离心惯性力推动骑手恢复原位，保证了骑手在侧向平面内的站立稳定性。

为分析此稳定过程，令方程(9a) 和(9c) 中Ω=Ω0，将ψ和φ视为扰动量，导出此线性方程组的特征方程

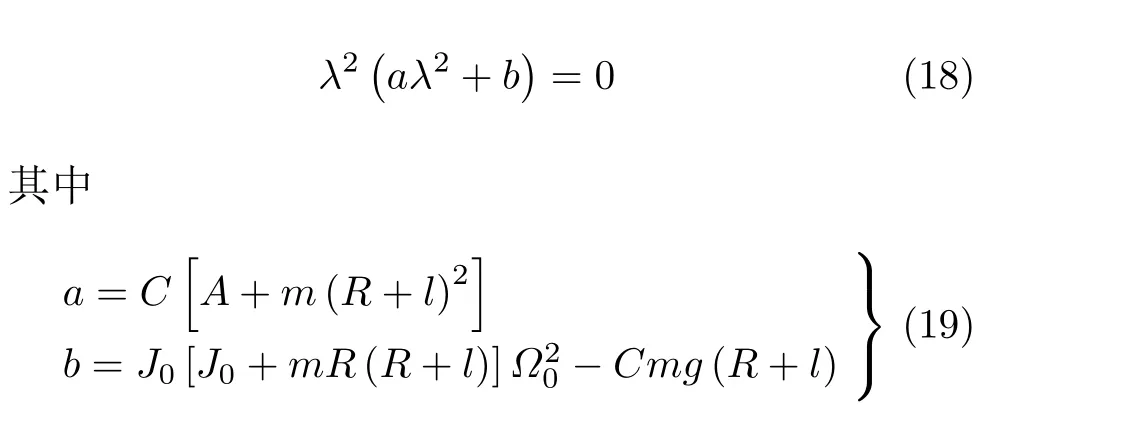
在方程(18) 确定的特征值中，λ= 0 的零特征值体现了变量φ因无恢复力导致的随遇性。另两个特征值的纯虚根条件为b ＞0，即ψ和φ耦合运动的零解稳定性条件。从中导出车轮的最低转速

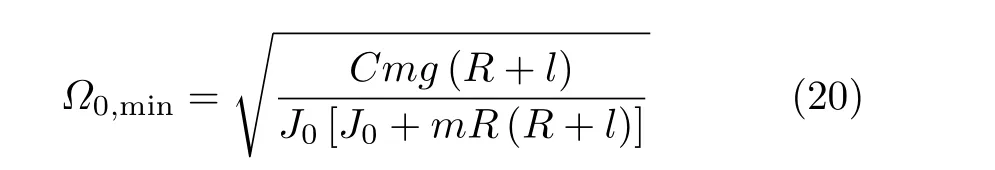
只要使车轮转速满足Ω0＞Ω0，min，骑手对左右侧扰动的站立稳定性就能得到保证。

与前文对前后侧扰动的稳定性分析类似，线性系统的零解稳定不能判断原系统的稳定性。但实际上任何机械系统均难以避免阻尼因素，若在系统中增加与角速度 ˙ψ成比例的阻尼项，则线性系统的零解即转为渐近稳定。根据李雅普诺夫一次近似稳定性理论，未经线性化的原系统的零解亦渐近稳定。

以上对滑板车运动过程的分析表明，骑手的肢体动作或控制电机的驱动制动，最终均转化为重力和地面摩擦力对车体和骑手的作用。滑板车运动状态的改变是重力和地面摩擦力的作用结果。任何系统都不可能依靠内力改变运动状态。