作旋转运动功能梯度材料矩形Mindlin 板的刚柔耦合动力学建模1)
2021-12-31杜超凡郑燕龙周晓婷章定国
杜超凡 郑燕龙 周晓婷 章定国
*(扬州大学建筑科学与工程学院,江苏扬州 225000)
†(南京理工大学理学院,南京 210094)
功能梯度材料 (functionally graded materials,FGM) 是由两种或两种以上性能各异的材料组合而成,通过改变其体积分数来改变结构沿某一方向的性能,以实现结构不同位置的功能需求[1]。由于FGM在材料界面处的力学性能过渡平滑,能消除不必要的界面应力,为解决热障问题提供了有力的帮助,因此其性能优于由两种离散材料粘结在一起的复合增强材料,被研究人员广泛关注。这种固有的材料性能不均匀性给力学分析带来了很大的困难,以往针对各向同性、均匀材料引入和发展的力学概念和建模理论等已不再适用,需要进行探索和创新。由FGM制成的旋转叶片,如太阳能帆板、风力发电机叶片及航空发动机叶片等,其动力学特性必然有别于传统均质材料。因此研究该类结构在不同材料组分和梯度分布规律下的动力学特性,将为工程应用设计出理想的功能梯度材料提供理论指导,具有重要的理论意义和广阔的应用前景。
旋转叶片是典型的刚柔耦合非线性系统,越来越多的学者关注柔性叶片的大范围运动与自身弹性变形的刚柔耦合机理以及柔性体变形场的离散方法,对这些问题的研究已成为柔性多体系统动力学领域的热点和难点。自从Kane 等[2]揭示“动力刚化”现象以来,国内外许多学者均对板的刚柔耦合机理进行了多方位研究。刘锦阳等[3]从连续介质力学出发,基于Jourdan 速度变分原理,采用有限元法和假设模态法对均质材料旋转矩形薄板动力学响应进行了仿真,并对两种方法的结果进行了对比。Yoo 等[4]基于Kirchhoff假设,采用Rayleigh–Ritz 方法描述三个维度的变形,考虑纵向和横向变形耦合及运动引起的动力刚化效应,研究了旋转复合材料悬臂板的不同纤维角对固有频率和模态的影响。Niu 等[5]运用哈密顿原理结合一阶剪切变形理论和冯·卡门几何非线性研究了受横向激励作用下的简支功能梯度石墨烯复合材料圆柱板的非线性振动问题。Javani 等[6]基于Mindlin 板理论,采用广义微分求积法(generalized differential quadrature method,GDQM) 研究了功能梯度环形薄板的热致振动问题。Alireza 等[7]通过Kirchhoff假设和一阶剪切变形理论确立非线性方程和边界条件,运用GDQM 和Newton–Raphson迭代法对方程离散和求解,基于Crank–Nicolson 方案获得温度场的函数,研究了FGM 薄板遭遇温度突兀冷却的非线性热弹性瞬时响应。Li 等[8]和黎亮等[9]基于假设模态法,考虑不同功能梯度系数对动力方程的影响,先后研究了FGM 矩形薄板自由振动响应及弯曲和扭转之间的耦合模态和频率转向现象。刘璟泽等[10]采用Kirchhoff–Mindlin 理论假设剪切应变场规避剪切闭锁,使用有限元三角形单元进行变形场描述,对曲线加筋Kirchhoff–Mindlin 板自由振动进行了分析。Moita 等[11]使用有限元法分析了复合板FGM 层、压电层和具有黏弹性的核心夹层之间主动-被动阻尼[12]的振动问题,FGM 层和压电层皆用经典薄板理论建模,核心夹层使用三阶剪切变形理论建模。Mantari 等[13]基于只包含四个未知量的新型一阶剪切变形理论,通过哈密顿原理推导控制方程,对FGM 板进行了自由振动分析。Zhang等[14]采用摄动法,将压电复合材料矩形薄板在横向和面内激励下的复杂偏微分非线性运动控制方程转化为等效的可解非线性方程,进而分析了矩形薄板的运动响应。Subodh 等[15]基于动态刚度法对功能梯度矩形薄板的自由振动行为进行了分析。吴根勇等[16]基于经典薄板理论,考虑二次耦合变形量,采用有限元法对复合材料板进行离散,建立了作大范围运动复合材料板的动力学方程,研究了材料铺层角度对复合材料变形的影响并和同性材料进行了差异对比。Li 等[17]和Akhras 等[18]均使用B 样条法对变形场离散,分别对压电层复合板进行了方法优越性分析和稳定性分析。杨兴等[19]从一阶剪切变形理论出发,使用有限元法对变形场进行离散,研究了作大范围运动功能梯度材料厚板的响应,并同经典薄板理论进行比较,验证了经典薄板理论的不足之处。然而,采用新的变形场离散方法,对考虑板剪切变形的旋转FGM 板动力学问题的研究比较少见。
本文采用无网格径向基点插值法[20-21]描述板的变形场,考虑材料非均匀性以及横向弯曲引起的纵向缩短,即非线性耦合项,利用浮动坐标系法[22],基于一阶剪切变形理论,运用第二类拉格朗日方程建立了作旋转运动FGM 矩形板的动力学方程。研究了作旋转运动功能梯度材料矩形板的动力学行为随功能梯度指数、转速、板纵横比的变化情况。同时对匀速转动的中心刚体与FGM 矩形板系统自由振动固有频率的频率转向问题进行了研究。
1 动力学建模
1.1 功能梯度材料
功能梯度材料通常是由两种材料混合而成,一种是陶瓷,一种是金属。对于FGM 矩形弹性板而言,假定其板上表面为陶瓷,下表面为金属,两表面的中间部分由这两种材料组合物构成。本文FGM 矩形板的材料表示如下:弹性模量E(z),材料的密度ρ(z),泊松比μ(z),可由下式表示[23]

式中P代表 FGM 矩形板某一位置的物理特性E(z),ρ(z),μ(z),Pc和Pm分别代表FGM 矩形板上表面z=h/2 和下表面z=-h/2 陶瓷材料和金属材料的物理特性,h为板厚度,V代表陶瓷材料的体积分数,N(N≥0) 为FGM 从上表面过渡到下表面的梯度指数。
1.2 运动学描述
图1 为在空间中作大范围运动的FGM 矩形板模型。其中O-XY Z为惯性坐标系,o-xyz为连体坐标系,且连体坐标系所在平面x-o-y与FGM 板未变形前中面重合,e1,e2,e3分别为连体坐标三个坐标轴的单位矢量。FGM 板长为L,宽为H,厚度为h,密度为ρ(z),弹性模量为E(z),泊松比为μ(z)=μc=μm=μ。
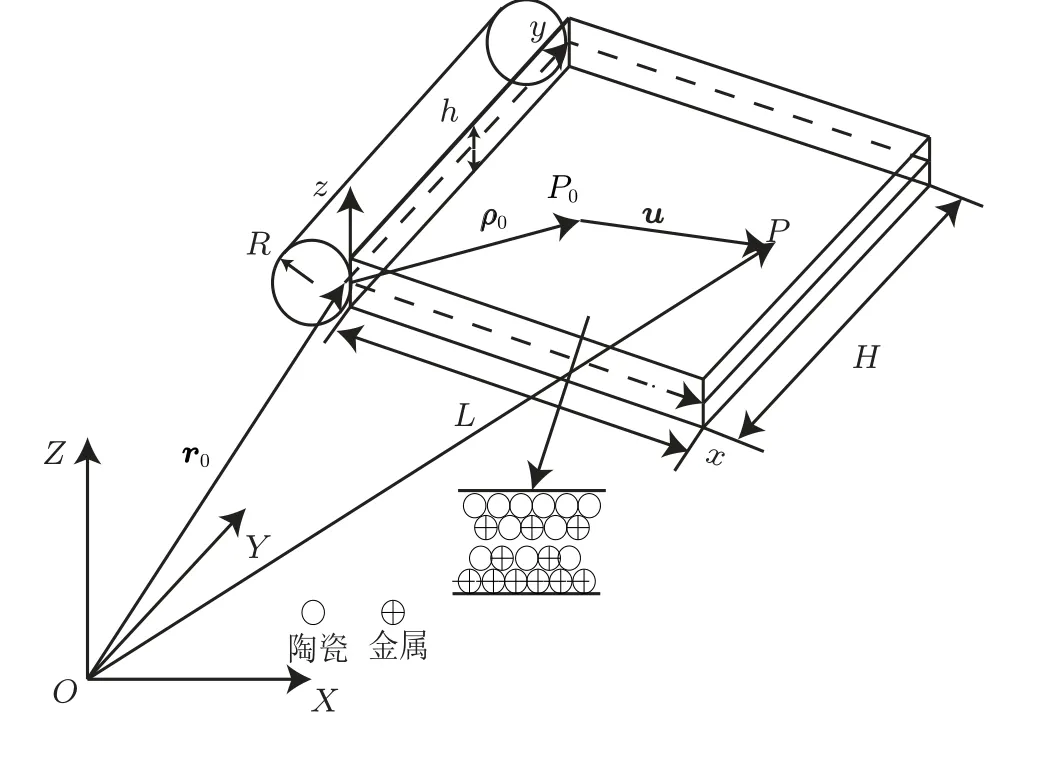
图1 作大范围运动FGM 矩形板
R为中心刚体半径,r0为连体坐标系原点在惯性坐标系中的矢径,ρ0为点P0在连体坐标系中的位置。现假定P0点为矩形板变形前板内任意一点,变形后为P,变形矢量为u,在连体坐标系下的分量为(u1,u2,u3)。其中纵向位移u1,u2可表示为

式中,VO和ωA分别为连体坐标系相对于惯性坐标O-XY Z的速度和角速度矢量,VP A为P点相对连体坐标系的速度矢量。则P点相对于惯性坐标系O-XY Z的速度矢量为


其中κ为剪切修正系数,取值为κ=5/6。
1.3 系统的动能和势能
FGM 矩形板的动能为

将式(5) 和式(6) 代入式(9) 得

1.4 FGM 矩形板变形场的离散
常用的矩形板变形场离散方法有假设模态法和有限元法,而本文采用无网格法中的径向基点插值法(radial point interpolation method, RPIM)。对于问题域Ω中的连续场函数u(x),可以用在该问题域中相关点的基函数表示如下
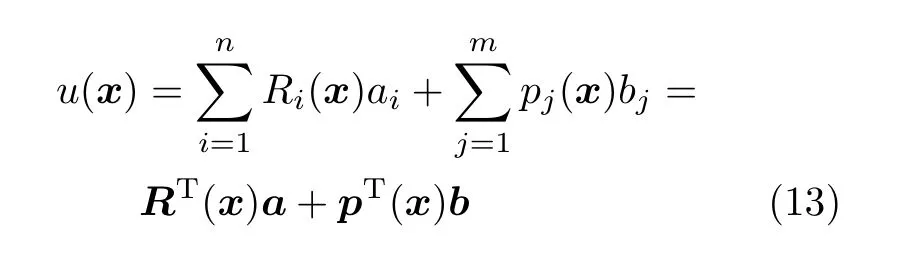


式中dc为计算点x同其局部支持域中的节点的间距的均值。
矩形板问题域中任意一点的变形可以表示为
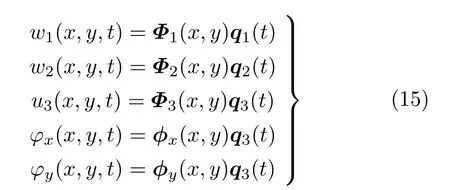

式中下标“,” 表示对坐标求偏导数。
1.5 FGM 矩形板刚柔耦合动力学方程
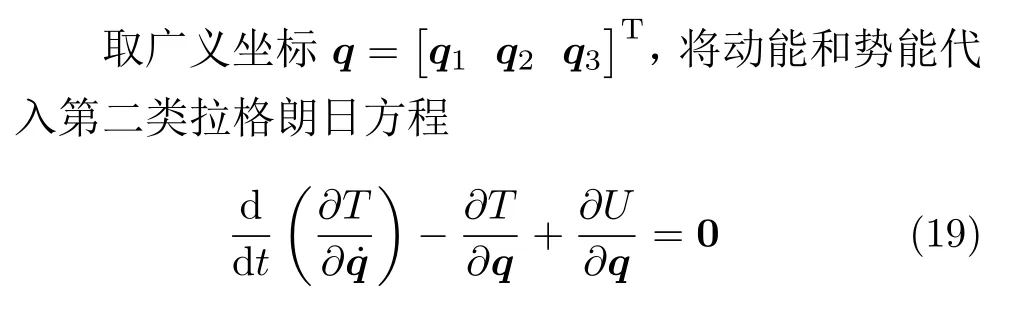
得到FGM 板的刚柔耦合动力学方程为
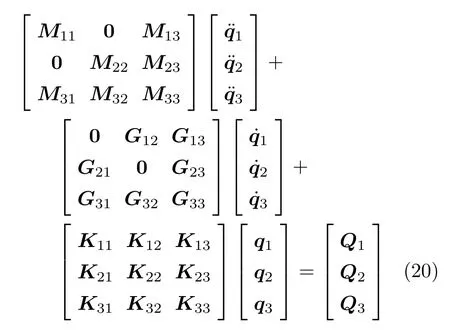
式中各分块矩阵为

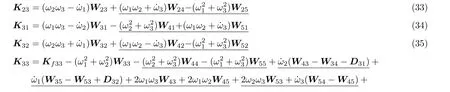
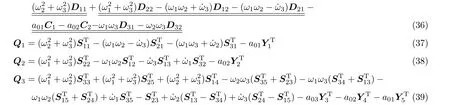
式中,a01,a02,a03为基点加速度在连体坐标系下的分量,表达式为


各分块式中双下划线项为考虑二次耦合变形量带来的附加动力刚度项。传统的零次近似模型建模时忽略了这些项,即这些项都为零。单下划线为考虑横向剪切变形所推导出的剪切变形项,若不考虑该项,则动力学方程退化为经典薄板理论。
2 数值仿真
2.1 功能梯度板“动力刚化” 研究
本节仿真一作大范围已知运动的悬臂FGM 矩形板, hub-FGM 板系统的材料参数: 长L=1.828 8 m,宽H=1.219 2 m,厚度h=0.02 m,ρc=3000 kg/m3,ρm=2707 kg/m3,Ec=151 GPa,Em=70 GPa,泊松比μ=0.3,中心刚体半径R=0。矩形板节点划分沿x和y轴分别以16 和8 个节点均匀分布,积分网格沿x和y轴分别均匀划分8 格和6 格,假设模态法(assumed mode method,AMM) 和三角形单元有限元法(triangle finite element method,TRFEM) 分别取5×7 阶模态和2×16×8 个单元。给定角速度规律为:ω1=ω3= ˙ω1= ˙ω3= 0,ω2=ω,˙ω2= ˙ω。其中

式中,时间T=30 s。
若只考虑FGM 板沿厚度方向上的横向振动,系统的动力学方程可简化为

图2 和图3 是角速度分别取Ω=3 Hz 和10 Hz,板功能梯度系数N分别取1 和2 的零次近似模型和一次近似模型计算得到的板外侧角点的横向变形图。从图2 中可以看出,本文模型的计算结果与文献[9] 基本吻合,但是在最大变形处,计算结果存在微小差异。这是因为文献[9] 是基于经典薄板理论,而本文是基于考虑剪切变形的Mindlin 板理论,因而系统更显柔性,所以最大变形处偏大。比较图3(a)和图3(b) 可以看出,Ω=3 Hz 低速运动时,不考虑附加刚度项的零次近似模型计算结果收敛,当运动为高速运动Ω= 10 Hz 时,零次近似模型的计算结果则发散,而一次近似模型的结果依然收敛。说明未考虑附加刚度项的零次近似模型只适用于低转速工况,而一次近似模型既适用于低速,又适用于高转速工况。
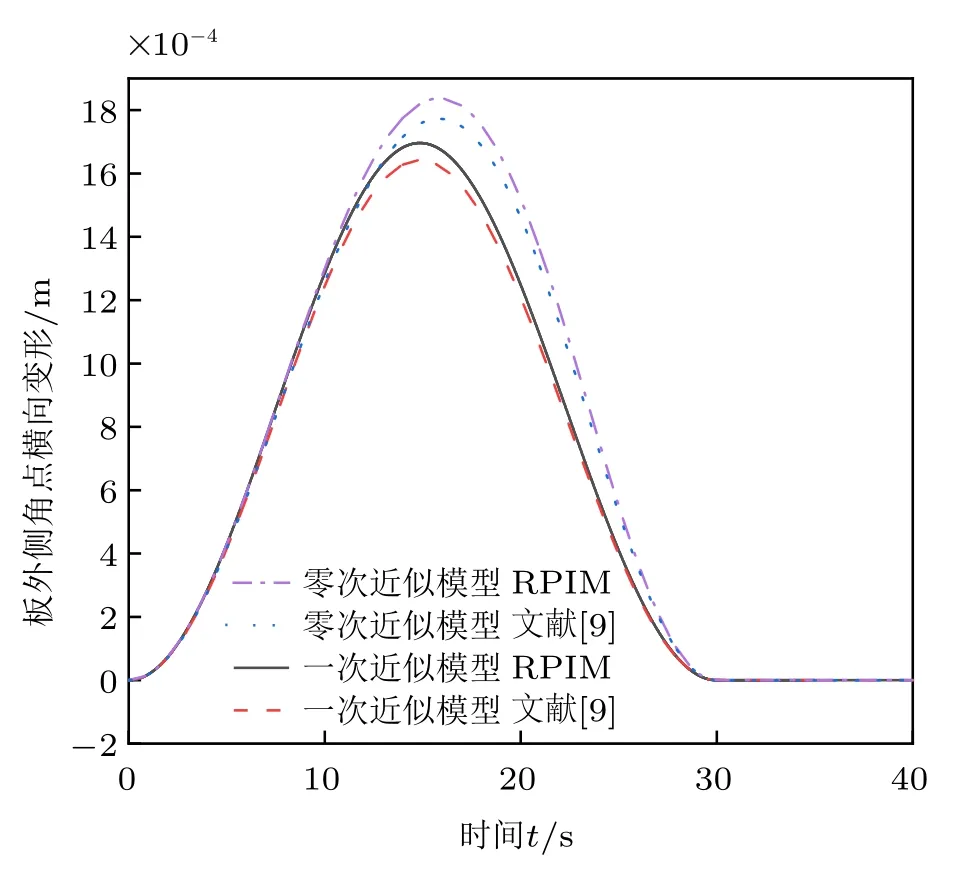
图2 N =1,Ω =3 Hz 时矩形板外侧角点横向变形

图3 N =2 时矩形板外侧角点横向变形
图4 和图5 是N= 2,角速度Ω= 3 Hz 和10 Hz 时一次近似模型得到板外侧角点横向变形速度。从两图中可以看出三种离散方法的仿真结果基本一致。进一步说明了本文所建模型的正确性。

图4 N =2,Ω =3 Hz 时板外侧角点横向变形速度
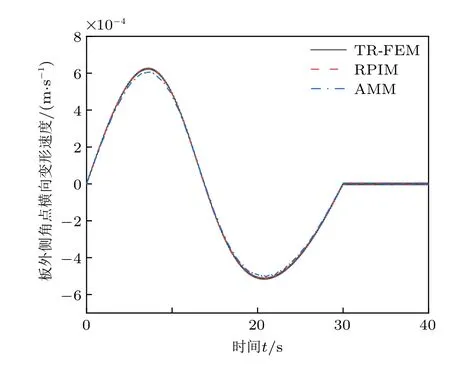
图5 N =2,Ω =10 Hz 时板外侧角点横向变形速度
图6 为Ω= 10 Hz,h= 0.002 m,Ec=15.1 GPa,N= 1,其余参数不变的FGM 矩形板外侧角点横向变形图。从图中可以看出,TR-FEM和RPIM 的结果在前10 s 基本一致,但随着时间的增大,TR-FEM 结果发散。而RPIM 的结果仍然收敛,说明了RPIM 有更好的计算稳定性,在同等计算条件下比TR-FEM 更有计算优势。
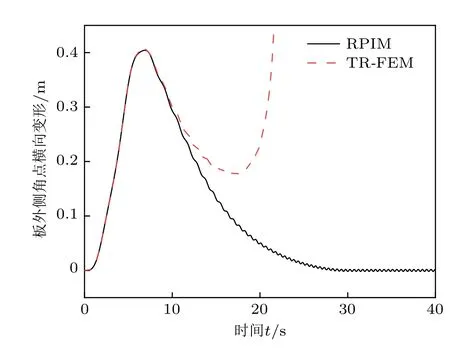
图6 矩形板外侧角点横向变形图
图7 分别给出了在Ω= 3 Hz 和Ω= 10 Hz 时板外侧角点的横向变形随功能梯度系数的变化情况。从图中可以看出,当N= 0 时,功能梯度板退化为均质板,板的最大变形最小,随着N的增大,板外侧角点变形也增大,说明功能梯度系数能影响板的柔性,功能梯度系数越大,板的柔性越大。
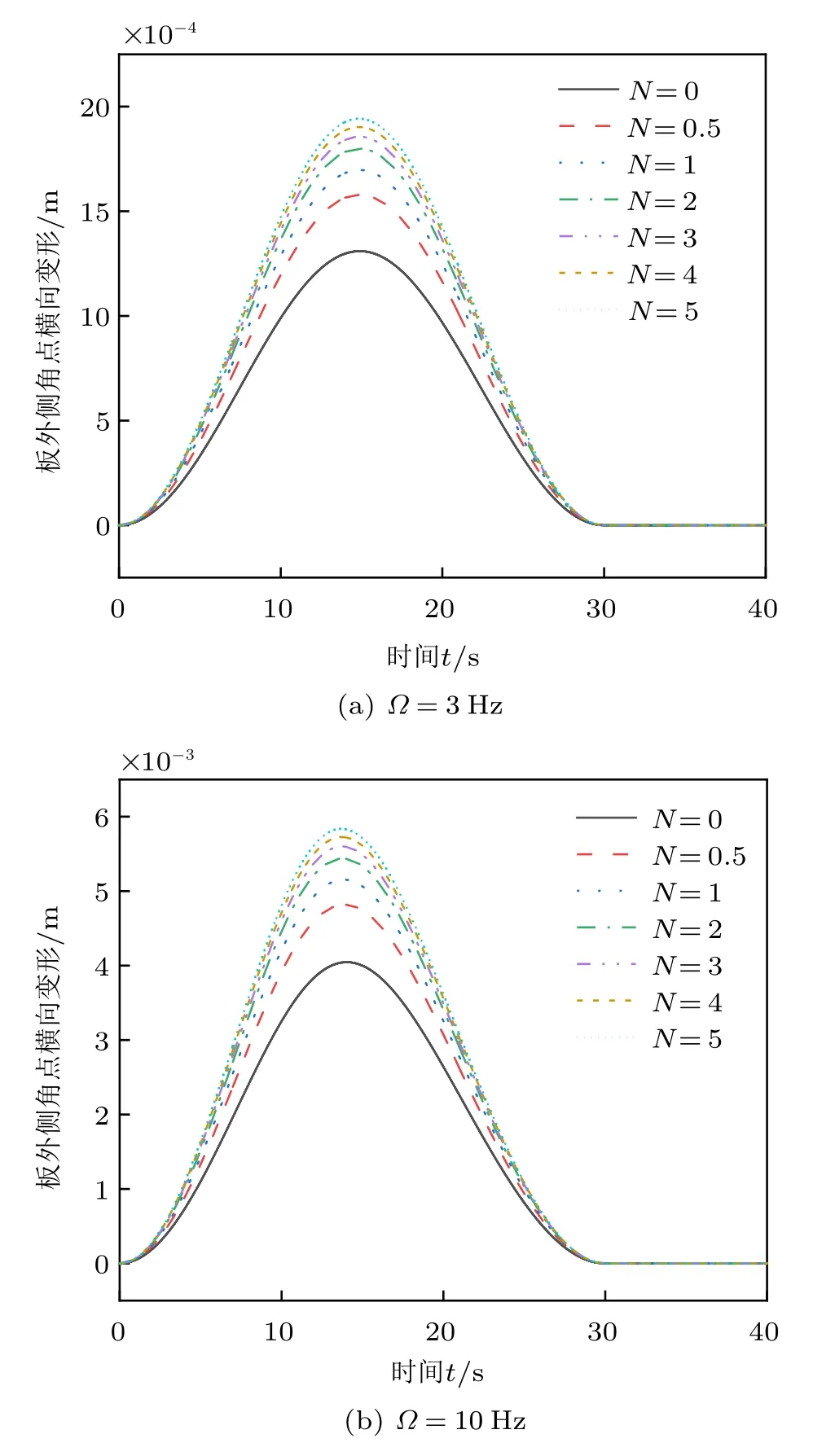
图7 不同功能梯度系数下矩形板外侧角点的横向变形
2.2 功能梯度板的固有频率研究
假设中心刚体半径为R,中心刚体以角速度Ω绕y轴匀速转动,则在连体坐标系下,原点O的速度矢量为:(v1,v2,v3) = (0,0,-RΩ),(ω1,ω2,ω3) =(0,Ω,0)。
若只考虑矩形板的横向振动,则基于Mindlin 板理论推导的作定轴转动矩形板的自由振动方程为
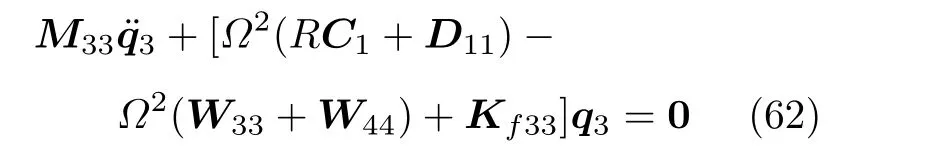
考虑到矩形板几何尺寸对固有频率的影响,定义如下无量纲变量:τ=t/T,χ=x/L,ζ=y/H,Z=q3/L,δ=L/H,η=h/L,σ=R/L,λ=Ec/Em,ϑ=ρc/ρm,ϖ=ωT,γ=ΩT。
将上述无量纲变量代入式(62) 得

为进一步验证本文所建模型的正确性,将功能梯度板退化为匀质薄板,同文献[25] 中的计算结果进行比较。表1 为δ=1,η=0.01,σ=0,中心刚体悬臂板无量纲角速度γ=1 的前五阶无量纲固有频率。由表1 可知,本文结果同文献[25]基本吻合,且由于考虑剪切变形,系统更偏柔性,固有频率比文献中的结果都偏小。表2 为δ=1,η=0.01,σ=0,N=2,不同无量纲角速度γ下中心刚体FGM 悬臂板前三阶无量纲固有频率。由该表知,随着无量纲角速度的增大,三种方法的无量纲固有频率皆增大,且基于一阶剪切变形理论的RPIM 结果总是比基于经典薄板理论的假设模态法的数值小,说明忽略剪切变形的经典薄板理论总是高估了系统的固有频率。表3 为δ= 1,η= 0.01,σ= 0,γ= 10,N取不同值时,中心刚体FGM 悬臂板前五阶无量纲固有频率。结果表明,随着N的增大,系统无量纲固有频率减小,进一步说明功能梯度系数越大,系统的柔性越大。

表1 作定轴转动中心刚体悬臂板的前五阶无量纲固有频率(δ =1,η =1,σ =0,γ =1)

表2 作定轴转动中心刚体FGM 悬臂板的前三阶无量纲固有频率(δ =1,η =0.01,σ =0,N =2)

表3 作定轴转动中心刚体FGM 悬臂板的前五阶无量纲固有频率(δ =1,η =0.01,σ =0,γ =10)
图8 所示为δ=5,η=0.01,σ=1 时,均质悬臂板前五阶无量纲固有频率随无量纲角速度的变化图。从图中可以看出,各阶无量纲固有频率皆随无量纲角速度的增大而增大,而且在第二阶和第三阶无量纲固有频率有频率转向现象。从放大图8(b) 可以看出,第二阶和第三阶固有频率没有发生交叉。

图8 均质悬臂板前五阶无量纲固有频率(δ =5,η =0.01,σ =1)
图9 为δ=5,η=0.01,σ=1,N=2 时,FGM悬臂板前八阶无量纲固有频率随无量纲角速度变化图。从图9(a)中能观察到随着无量纲角速度的增大,多阶无量纲固有频率发生了显著的频率转向现象,而从频率转向区域的局部放大图9(b)~9(d)中可知,发生频率转向的相邻两阶频率并没有交叉。

图9 FGM 悬臂板前八阶无量纲固有频率的变化情况(δ =5,η =0.01,σ =1,N =2)(续)
图10 为δ=1,η=0.01,σ=1,N=2 时,FGM悬臂板第六阶到第八阶无量纲固有频率随无量纲角速度变化图和局部放大图,从图10(a)看到第七阶固有频率同第六阶和第八阶固有频率发生了多次转向现象,说明板的纵横比对系统固有频率的频率转向影响较大。
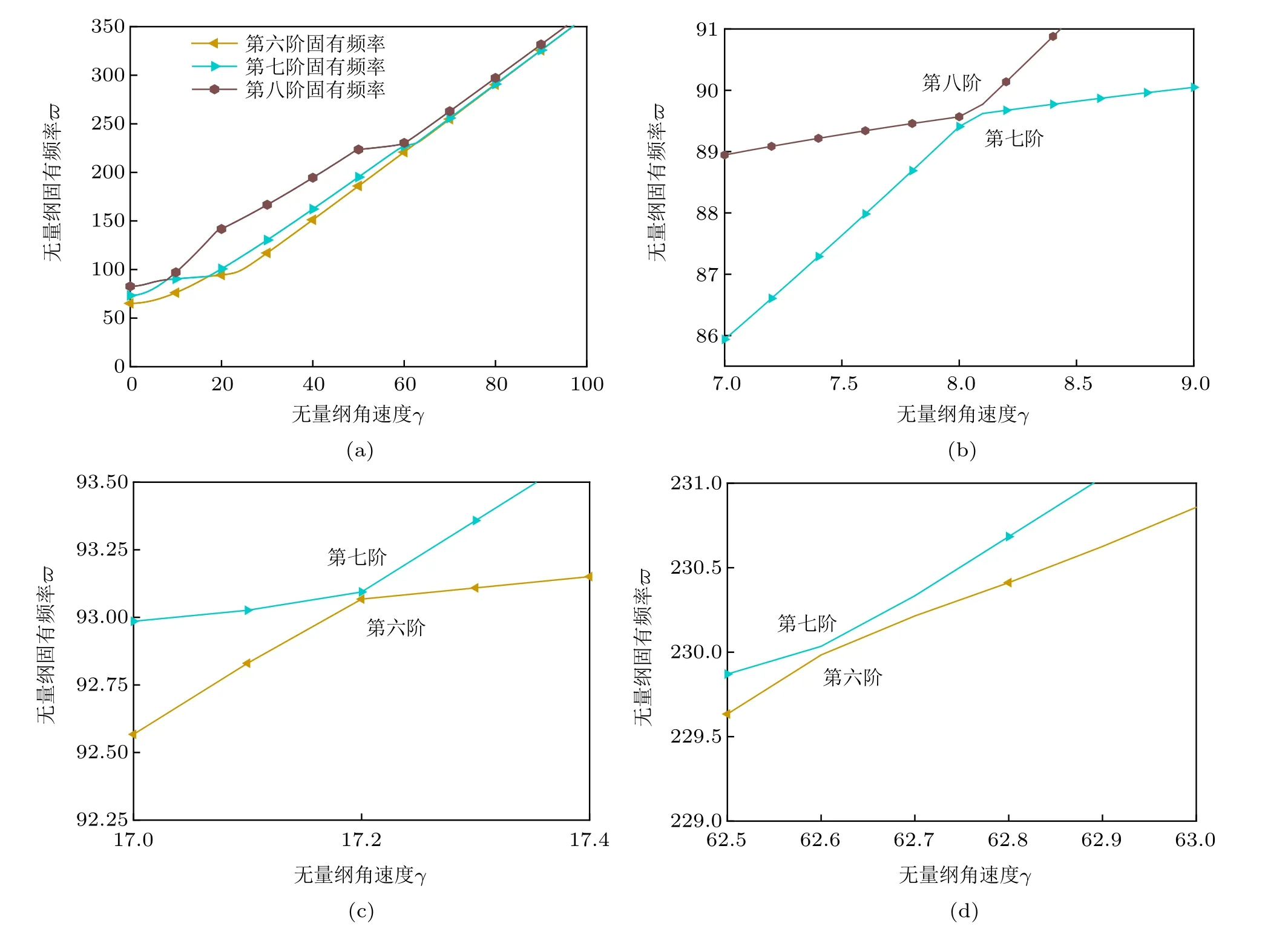
图10 FGM 悬臂板第六阶到第八阶无量纲固有频率的变化情况(δ =1,η =0.01,σ =1,N =2)
3 结论
(1)采用RPIM 描述柔性板的变形场,基于一阶剪切变形理论,建立了旋转FGM 矩形板的刚柔耦合一次近似模型。该模型既适用于低转速情况,又适用于高转速情况,既适用于薄板问题,又适用于中厚板问题。在同等计算条件下,RPIM 相比TR-FEM 更具有计算优越性。
(2) 随着功能梯度指数的增大,旋转FGM 矩形板的横向弯曲变形变大,固有频率减小,说明功能梯度指数的增大使系统的柔性增大,可通过改变功能梯度指数的取值范围以达到控制变形及频率的目的。
(3)基于经典薄板理论的无量纲固有频率总是大于基于一阶剪切变形理论的无量纲固有频率,说明忽略剪切变形的Kirchhoff假设使结构更偏刚性,总是高估了系统的固有频率。
(4)系统的无量纲固有频率会随着转速和板纵横比的变化而发生频率转向现象。不仅有单次转向,还有多次转向现象,且发生频率转向的相邻两阶频率并不相交。
