清末民初八闽数学家陈平瑛“积较开方新术”研究

高红成 霍云娟

(1.天津师范大学 数学科学学院，天津 300387； 2.内蒙古师范大学 科学技术史研究院，呼和浩特 010022； 3.天津市第六十三中学，天津 300190)

晚清，中国数学逐步走向近代化。一方面，诸如解析几何、微积分、符号代数、概率论等西方数学传入中国，逐渐被中算家承认、理解、吸收和运用；另一方面，中国传统数学受到西方数学概念、方法的影响，逐渐被“西化”，最终被取代，如天元术、垛积术等领域。[1]不过，这个近代化过程是复杂的，面对近代西方数学的“优势”，传统数学并非“一边倒”地立即被取代，有的甚至还有所发展，出现一些有特色的成果，如华蘅芳(1833—1902)所创造的积较术。本文要讨论的陈平瑛“积较开方新术”则是华蘅芳积较术的发展。

陈平瑛是清末民初福建数学家。郭金彬在《清代八闽数学家略论》[2]中对他做过简单介绍。笔者在《代数布式，天元开方——卡尔达诺公式在晚清的境遇》[3]中讨论了陈氏对卡尔达诺公式的理解和应用，在《〈中西算学题镜〉研究》[4]中对陈氏的数学著作《中西算学题镜》进行了较为全面的论述，对积较开方新术也有初步的解读。上述研究或没有论及陈氏积较开方新术，或是对其中蕴含的数学思想挖掘不够，特别是对这个方法与陈氏本人对垛积术的研究之间的关系揭示不够。本文先利用新史料考订陈平瑛的生平，其次讨论陈氏对垛积术与招差术的研究创见及其思想来源，然后考察陈氏“零边积较”的构造及其“简商之法”，接着讨论陈氏还原表以及“径求开方之法”，最后对这一成果的历史意义进行评述，以期对陈氏积较开方新术的数学意义和历史意义有更深入的认识。陈氏著作采用了晚清李善兰(1811—1882)、伟烈亚力(A. Wylie，1815—1887)共创的汉译代数符号(正文中有示例)，为了便于讨论，本文改用现代的数学符号进行表述。

1 陈平瑛生平考证

陈平瑛，字修常，号仲容，福建侯官(现属福州市闽侯县)人，清末民初数学家，数学著作有《中西算学题镜》(1901)8卷[注]光绪三十二年(1906)八月十二日，陈氏曾将《中西算学题镜》赠送给时任广州府中学堂监督的丘逢甲。[5][6]、《直乘法》(1916)[注]按陈平瑛序言记载，此书为他《算学观海》5种的第一种。《算学观海》1914在年德国柏林图书赛会、1915年在巴拿马图书赛会展出。另，1914年《广东教育公报》第5期报道了陈平瑛请德国驻广州领事代为转寄参会的新闻。[7][8]。关于陈氏的生平，以往的研究[2，4]只有一些简短的介绍，现基于部分新发现的史料做一些订正和补充。

首先是陈平瑛的生年。陈氏在其《直乘法》的序中称：“中华民国二年十一月闽侯陈平瑛仲容自序于广州，时年三十有五。”[8]又，卢朋著在光绪壬寅(1902)四月为《中西算学题镜》作序称赞陈氏“今年才二十四，大集彬彬，又成不朽盛业”。([6]，卢朋著序) 卢朋著(1876—1839)，名雄飞，广东新会(现江门市新会区)人，近代著名的中医教育理论家。早年好算学，著有《算学心得初集》、《算学讲义》。[9]卢氏与陈氏为世交，年少时“同习算”，“比长尝共事学堂”，二人给对方著作写序时互以“同谱兄弟”相称。[10]“中华民国二年”(1913)35岁，“光绪壬寅”24岁，两条史料相互印证，可以推定陈氏生于1879年。[注]我们曾认为陈氏生于1881年[4]，所据为网络资料，在此依据新发现的史料予以订正。

其次补充陈氏的一些生平信息。卢朋著曾介绍说：

仲容之家学渊源盛矣。遵甫谨庵先生斐然有作，既著《算珠》，近复成《天学题镜》，启诱来兹。令昆伯达、令弟怀祖俱深于形代。仲容幼即嗜算，七八岁时便日以白垩涂塾壁作几何图，长更博涉英文，孶孶不倦。([6]，卢朋著序)

卢氏还称陈氏“一门之内，父子兄弟孜孜为学，而于几何天算之艺治之尤专。”([11]，卢朋著序) 可见，陈家可谓数学世家。陈平瑛本人自幼喜好数学，有数学著作出版；其兄陈修龄，号伯达，有《公式演算》5卷(1905)[11]传世；其父有数学著作《算珠》、《天学题镜》；其弟怀祖对几何和代数有研究。

根据《福建乡试录(光绪丁酉科)》记载，陈平瑛参加福建省丁酉(1897)科乡试，中式第75名。[12]他第三场的天文算学策问优异，为世人称道。他的学生马麟书说他“生而颖悟，幼通算理，年未弱冠，以算学名天下，其丁酉科闱中所对天算策问，传诵于时。”([6]，马麟书后叙) 卢朋著也称“仲容丁酉举于乡，已以天算作惊人一鸣。”([6]，卢朋著序) 又，陈平瑛后来给黄启明(字佩星)的《微积通诠》一书作序称：“岁甲辰，余课算于广州府中学堂，花县黄君佩星惠然造访，谈论数理，彼此甚欢。”[13]在其自著的《直乘法》“又序”中称：“民国三年四月任职数学教员于广东高等师范学堂。”[8]从这两条史料可知，陈氏曾前后在广州府中学堂和广东高等师范学堂任数学教师。陈氏懂英语，《中西算学题镜》卷8“几何”就是其译作。

《中西算学题镜》(以下简称《题镜》)是陈平瑛的代表作，兼及“发明古义”和“独创新术”([6]，卢朋著序)。陈氏对传入的微积分、代数学都有很深刻的认识，如他对《代数术》中卡尔达诺公式的理解和把握是同时代中算家中的佼佼者。[3]他的“积较开方新术”是他对垛积术(卷3“论垛积之理”)和开方术(卷4“论开方之理”)综合研究的成果。

2 陈氏垛积公用表与朱世杰招差术的推广

2.1 朱世杰招差术的推广：“一切垛积之题皆以此法通之”

由于符号代数学和微积分学的传入及其影响，特别是符号代数在数学表示上的优越性，晚清数学家对垛积术、招差术的一般性的认识越发清晰。

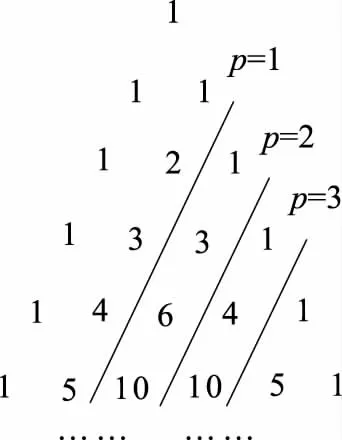
图1 p乘三角垛 (贾宪三角形)

(1)

式(1)是垛积术的基础。([1]，345页)

同时，晚清数学家逐渐认识到朱世杰招差术的一般性，即这个方法给出了解决一类垛积求和问题的算法：先将给定的垛积分解为若干“乘数递次增一，项数递次减一”的p乘三角垛(p=3，2，1，0)，然后再依据式(1)求和。根据其分解规律，各阶差分即为分解出的各p乘三角垛的个数，即“所招各差”，其中“初差(上差)”为垛积首项。[14]

陈平瑛《题镜》卷3“专论垛积之理”，所用垛积名称承续李善兰的《垛积比类》。他明确指出，朱世杰招差术可以推广到解“一切垛积之题”，而不仅仅局限于解“乘方垛招兵”一类的题。他说：

原术(指朱世杰招差术)专为解“乘方垛”、“招兵”一类题而设。今因《四元玉鉴》中“岚峰落一”门类颇多，学者每苦难于记忆，因为推广原术，一切垛积之题皆以此法通之。执简驭繁，无待探索，亦习是术者之一快事也。([6]，卷3: 2b页)

他的做法就是，先一律将所求垛积分解为若干p乘三角垛(即便是按p乘三角垛规律给出的垛积也如此)，再基于式(1)求和。以《题镜》卷3第4题为例，原题为：

今有茭草八千五百六十八束，欲令撒星更落一形垛之，问底子几何？([6]，卷3: 9b页)

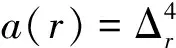
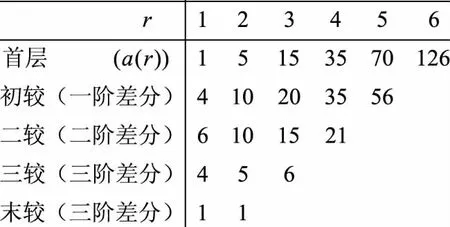
图2 朱世杰招差术求诸差(r从1开始)

(2)

两边对r求和，由式(1)有

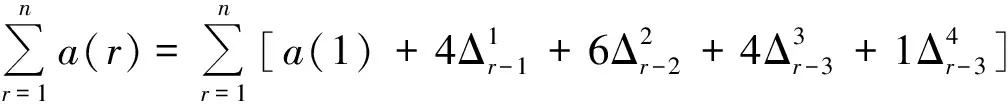
(3)

要求出“高”(n)，一般方法是，先得到关于n的开方式，最后运用开方术解出n。根据已知条件有

(4)

(5)

展开、合并，可得开方式:

n5+10n4+35n3+50n2+24n=120×8568

(6)

开五次方得n=14。原题得解。

陈平瑛何以看出招差术的一般性呢？他在《题镜》卷3第1题“注文”指出他思想的来源：“解题之理，则从嘉善陈氏‘垛积’、‘招差术’推出。”([6]，卷3: 2b页) 这里的“嘉善陈氏”指的是陈维祺，生卒年不详，曾从数学家刘彝程(约1840—？)学习算学。《中西算学大成》是陈维祺主持编纂的一部大型算学类书，较为全面地系统汇集了当时中西数学主要内容，共100卷，由刘彝程“鉴定”，1889年由上海同文书局石印刊行。

陈平瑛提到的“垛积”、“招差术”分别指的是《中西算学大成》卷43“天元术四”的两节内容：“朱氏垛积”和“垛积招差术解”。前者摘录《四元玉鉴》中的垛积术和招差术，共11题。后者是对招差术的解释。陈维祺解释道：“松庭朱氏《四元玉鉴》中‘如像招数’五问为垛积最精奥之理。……尝深思而得其理，不外求诸方积各层之较数，亦不外三角平立各垛之各层。洞悉其原，势如破竹。”[15]为说明“洞悉其源”，陈维祺运用晚清的代数符号，给出了一个“三乘方招兵”(即按自然数4次方规律招兵)的例题，仿照招差术思路进行解答并给出了算法分析。该题虽依然局限于招兵，但通项次数比朱氏“立方招兵”高了一次，从三次升到四次，朱氏招差术的一般性已昭然若揭了。显然，陈平瑛在陈维祺的基础上更进一步，将招差术大胆地推广到解“一切垛积之题”。

需要指出的是，陈平瑛以为“垛积招差术解”是陈维祺所作，并不确切。数学家周达(1879—1949)曾记载说“闻之沈君立民云”，这个术解“本于兴化刘省庵先生”。[16]沈立民(生卒年不详)，即沈善蒸，浙江桐乡人，也曾从刘彝程(字省庵)学习算学，后在上海广方言馆任副教习，为刘彝程的助手。[17]刘氏对垛积术很有研究，成果颇丰，沈善蒸、陈维祺都是刘彝程的学生，周达的记载应该可信。这样，可以画出朱世杰招差术被明确推广的研究路径：刘彝程→陈维祺→陈平瑛。

2.2 垛积公用表：多项式差分形式到幂和形式的过渡矩阵

从式(4)到式(6)的运算过程中，涉及多项式乘法、通分、同类项合并等运算，这在筹算和晚清汉译数学符号系统中，演算均有诸多不便。陈平瑛说：“各项连乘后复相加减，其法必甚繁重，而几至不能用。”([6]，卷3: 4a页)

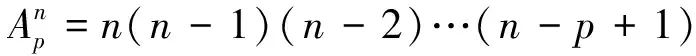
表1 垛积公用表(n从1起算)

图3 差分形式变形为幂和形式的表格算法

这个“横乘竖加”的过程用现今的矩阵乘法可以表示如下：

=24n+50n2+35n3+10n4+n5

(6′)

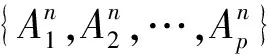
综上可知：第一，陈氏明确地把朱世杰招差术推广到任意的高阶等差数列求和，相当于求出多项式的差分形式(与牛顿向前插值公式相当)，最后基于(1)式求和。第二，构造了“垛积公用表”，基于此表进行“横乘竖加”，可以很快地将多项式的(弱)差分形式化为幂和形式。陈氏对此表颇为自得，认为它“以之推一切垛积之题，无不可通，诚可为垛积公用之表。”([6]，卷3: 5b页)

3 陈氏积较表以及“简商之法”

垛积“有积求高”题，若要用开方术求解，则最后的开方式须是从上到下降幂排列的幂和形式。这样做之前需通过多项式变形或者利用“垛积公用表”把差分形式的式(5)变形为式(6)。华蘅芳曾创造了积较术从另外一个角度解决这个问题。该术先给出一种求多项式在零点的差分表达式的方法，这个表达式相当于多项式的牛顿向后插值公式，其系数被称为“零边积较”；由“零边积较”可得到多项式对应方程的差分表，即所谓的“积较表”；该表具有减根变换的作用，华氏最终运用它求解方程的整数根。[18]华氏积较术是传统数学中的招差术和开方术在晚清的发展，很有影响，学界对此的研究颇多。[18- 22]陈平瑛洞悉华氏积较术用以“开方”的本意，但他认为华氏原法“太觉繁重，因变通其例，别演新术”，在《题镜》卷4也给出了一种通过方程的零边积较和积较表来解方程的算法，陈氏称其为“积较开方新术”。([6]，卷4: 16b页) 陈氏所用术语仿照华氏，不过数学意义有所不同。

3.1 陈平瑛的“零边积较”和“积较表”：“加减”求根

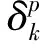
表2 陈氏积较表(n从0起算，原表略)

因为多项式是系列np的线性组合，运用积较表可以较快地得到多项式的零边积较，进而“依次加减”得到整个差分表。以陈氏解开方式(7)为例进行说明。

n3-8n2-13n+140=0

(7)

取表2的前4行，按图4所示程序进行“横乘竖加”，可以得到式(7)的零边积较(140，-20，-10，6)，对应的方程陈氏称为“积较式”，即式(8)。

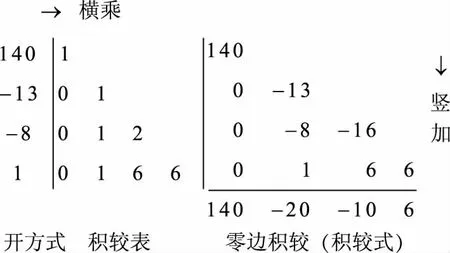
图4 多项式方程化成零边方程的表格算法

(8)

既得到零边积较，便可以递推出(8)“增率为一”(n=0，1，2，…)的整个差分表(积较表)，部分如表3。

表3 积较式的积较表

由表3可以看出n=5和n=7是开方式(7)的两个根。

同样地，图4“横乘竖加”的过程若用矩阵乘法可表示如下：

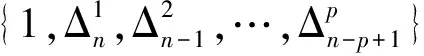
方程(7)的零边积较还可以直接通过朱世杰招差术得到，程序参考图2。零边积较无论是直接得到还是通过积较表获得，目的是通过“加减”求得整个差分表(积较表)，因为差分表具有减根变换的性质，这样就能得到方程的根。

陈氏零边积较与华氏零边积较没有本质区别。前者可以看成多项式的牛顿向前插值公式的系数，后者相当于是向后插值公式的系数；在求各阶差分的具体操作时，前者将差写在减项之下，后者将差写在被减项之下。方程的根是根据零边积较“加减”而成的“积较表”得到，而不再是通过传统的(正负)开方术。

3.2 求零边积较的“简商之法”：基于多项式的嵌套形式

陈氏认识到，求方程的零边积较是一个关键步骤。他设计了一个程序，“不用积较表以求积较”，称之为“简商之法”。下面以他求方程(9)的零边积较为例进行说明。

n4+2n3-41n2-42n+360=0

(9)

方程按降幂排列后，前4项以(n-1)除，所得商的前3项以(n-2)除，所得商的前2项以(n-3)除，由此得到余数列{1，8，-28，-80，360}，分别依次乘以4!、3!、2!、1!、1，得到数列{24，48，-56，-80，360}，即为零边积较，对应的零边方程(积较式)为

(10)

“简商之法”的程序如图5所示。其运算的代数意义如下：

图5 求零边积较的“简商之法”

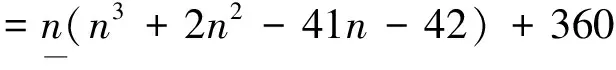
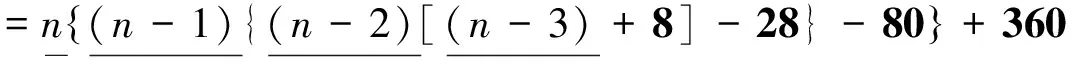
这个例子具有一般性。设多项式为p次，降幂排列，前p项用(n-1)除，所得商的前(p-1)项用(n-2)除，……，所得商的前(p-k)项用(n-k-1)除，……，所得商前2项用(n-p-1)除。各次除法后的余数列依次乘以p!、(p-1)!、…、1!、1，所得数列即为零边积较。

陈氏“简商之法”相当于先运用综合除法将多项式幂和形式逐步变形为嵌套形式，然后变形为差分形式，最终得到零边积较。相较于积较表的表格算法(图4)，“简商之法”更简捷，程序性更强，可操作性也很强。这是陈氏的一个创见。

4 积较还原表和“径求开方之法”

4.1 积较还原表：从差分形式到幂和形式

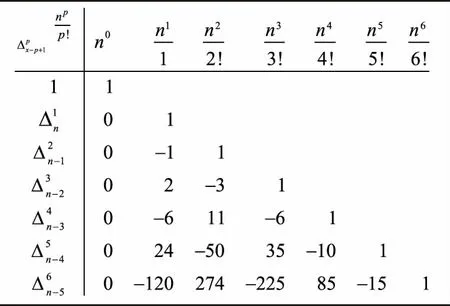
表4 陈氏积较还原表(n从0起算，原表略)

4.2 “径求方之法”：嵌套形式的展开

陈氏认为利用还原表求开方式还是比较麻烦，他设计了一个“径求开方之法”，更具有程序性。以前文的零边方程(10)为例进行说明，相应程序如图6所示。

图6 “径求开方之法”

陈氏先将零边积较24、48、-56、-80、360分别除以4!、3!、2!、1!、1，得到数列{1，8，-28，-80，360}，然后进行3次乘加运算：

第一次乘加：1乘以-3与8相加得5，5乘以-2与-28相加得-38，-38乘以-1与-80相加得-42，停止；

第二次乘加：1乘以-2与5相加得3，3乘以-1与-38相加得-41，停止；

第三次乘加：1乘以-1与3相加得2，结束。

最后得到数列{1，2，-41，-42，360}，即为开方式n4+2n3-41n2-42n+360=0各项的系数。

陈氏指出“径求开方之法”为“前法(简商之法)之还原”，实际上就是“简商之法”的逆操作，相当于将差分表达式按次数展开逐次合并同类项，最后得到幂和形式(开方式)，程序性强，省去了表格算法之繁。这也是陈氏的一个创新。

5 结 语

一般而言，传统数学中的垛积问题有两类：第一类，已知通项和项数(n)，求和，即所谓的“有高求积”。第二类，已知通项与和，求项数(n)，即所谓的“有积求高”。晚清垛积类的问题大多数是以第二类情形出现。中算家基本上都认识到贾宪三角形斜行(p乘三角垛，图1)的重要性质——式(1)，这是垛积术的基础。

第一类问题，是基于式(1)求和的，而式(1)左右两边多项式都是以差分形式表现出来的，所以这类问题需将通项化成差分形式才能求和，这是招差术的数理基础。第二类问题是第一类问题的逆问题，需要先按第一类问题求和，这时的和依然是差分形式，一般需要将这个差分形式转化为幂和形式(开方式)，最后运用开方术求解出“高”(n)。所以解决这类问题，要综合运用到垛积术、招差术、天元术、(积较)开方术，到晚清还需加上代数术。这也是陈平瑛“积较开方新术”虽然是开方方法，却要从垛积术谈起的原因。

陈平瑛从陈维祺的解读中将朱世杰招差术进行了推广。同时，他还深刻认识到了华蘅芳“零边积较”的来由和目的，故能用推广的朱世杰招差术来构造自己的“零边积较”，也给出了多项式幂和形式化成差分形式(积较式)的方法。

在陈平瑛(和华蘅芳)积较术中，“高”(n)不通过正负开方术得到，而是通过方程的差分表的减根变换的特性得到，理论上只要得到方程的差分表即可，但在实际操作时，方程根为多位数时，为节省计算，往往将方程按整十、整百做减根变换后，再将变化后的方程化成幂和形式的还原方程以求低位的根。这样也涉及多项式的两种形式的互化。 两种形式的互化从算法上讲是互逆的，这也导致了积较表与还原表(垛积公用表)之间的互逆关系。

陈平瑛“积较开方新术”是受到华蘅芳积较术启发得到的，两人的积较表和还原表数学意义一致，但陈氏有所变化和创新。第一，他设计的求零边积较的“简商之法”，程序性很强，省去了查积较表、进位退位之繁，简化了横乘竖加计算。第二，他设计的“径求开方式”的方法也很快捷，省去查还原表之繁。这两点可以看成多项式的差分形式与嵌套形式的互化算法和互逆程序。陈、华两种积较术都是源于中国传统数学中垛积问题引出的开方算法，目的是解方程。陈氏方法较之华氏的方法有更强的程序性。陈氏于垛积术和开方术的研究成果之间的关系可以用图7示意。卢朋著评价陈氏不仅能“发明古义”，还能“独创新术”，的确如此，也确属不易。

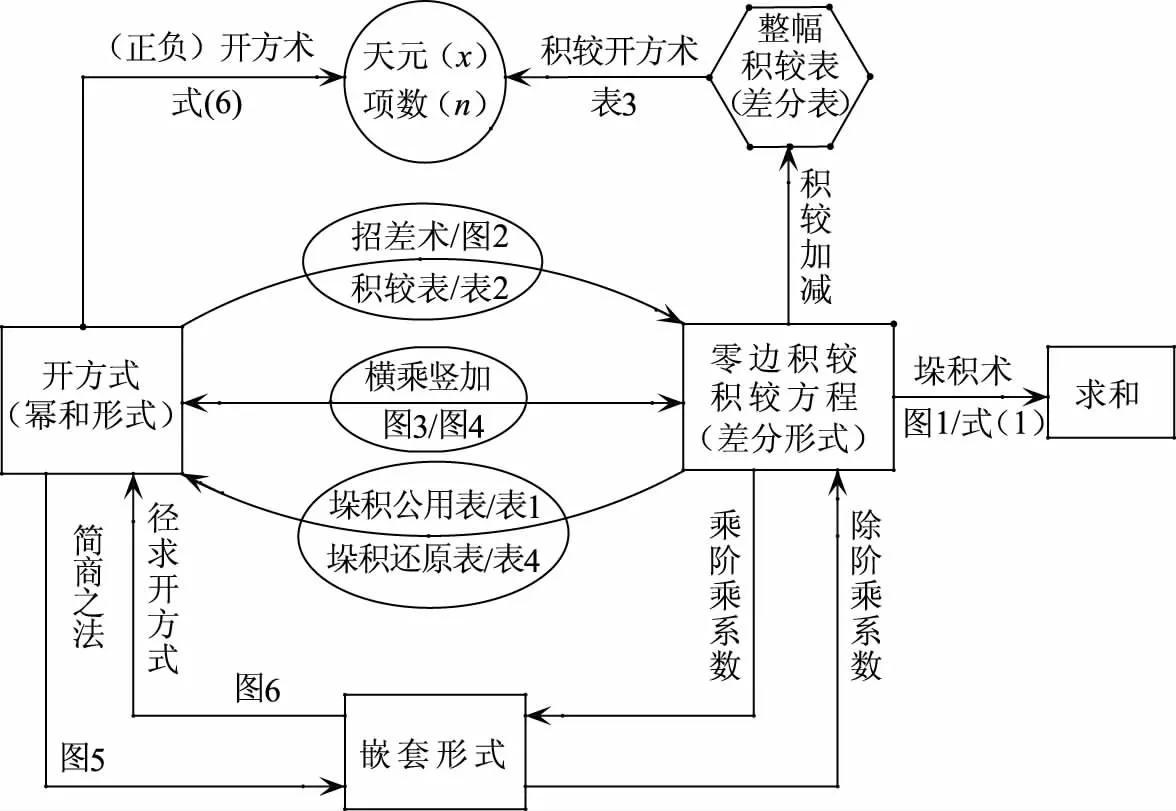
图7 陈平瑛垛积术、开方术研究成果关系图

我们注意到，及至晚清，传统数学逐渐“西化”，但开方术却还有较强的生命力，屡有发展。例如，三次方程的求根公式(卡尔达诺公式)和四次方程求根方法通过《代数术》的翻译而传入了中国。运用公式求解三次方程，遇到三个根均为实根的“不可约方程”时，虚数的三次开方运算就变得不可避免，这在西方数学传统中也是比较诡异的情形，并且五次及其以上次数方程没有一般的公式解。这时若用中国传统的开方术求解，反而“显得顺利”。因此晚清求解高次方程时，一般做法是，吸收了西方数学中方程的代数表示形式，中间的化简运算也是代数的，最后的开方却还是要求助于传统数学中的开方术(确切地说，是基于天元术的开方术)，即所谓的“代数列式，天元开方”。[3]因此，我们看到，传入的微积分、符号代数等西方数学虽然具有“优势”，但传统数学并没有立即被取代，甚至还有所发展，出现一些有特色的成果，华蘅芳积较术属此，陈平瑛的新术亦属此。

当然，陈平瑛这些有特色的成果，并不完全是传统数学的发展，他的表述方式、说理与推导过程均采用了传入的符号代数语言。这种语言很大程度上解决了传统数学中“言之甚繁，推之甚难”的问题，也有助于发现传统数学中算法的一般性和程序性，推动传统数学发展。这其实也是“西化”的表征。跨文化的科学传播有其复杂性，在传播过程中，科学知识本身的“优越性”并不起决定作用，传播者和接受者双方的特点决定了西方科学知识传播的特点和内容。([1]，371页) 长远来看，陈平瑛的成果虽富有特色，但依然是中国传统数学被取代的过程中一个过渡性成果，折射出传统数学近代化复杂的一面。

致 谢感谢中国科学院自然科学史研究所田淼研究员、邹大海研究员和匿名审稿专家提出的宝贵意见。