基于连续激光加热法测量金属材料的比热容

周 逸，林 鸿，冯晓娟，邱 萍，刘 薇，张金涛

(1.常州检验检测标准认证研究院，江苏常州213164；2.中国计量科学研究院，北京100029；3.郑州计量先进技术研究院，河南郑州450001)

1 引 言

随着工业化的快速发展，性能优质的金属材料如TC4钛合金、7075铝合金和T2紫铜等，在智能装备制造、航空航天等领域中被广泛应用。由于存在材料成分杂质等并非完全明确,新型合成材料并无参考数据等问题，研究者通过查阅文献和数据手册等获得的材料热性能参数[1,2]，常常与实际情况不匹配。因此，有必要通过实验测量获得待研究金属材料的热物性参数[3]。

比热容是对金属材料进行性能分析和结构设计时需要考虑的重要热物性参数之一，其测量方法主要有：量热计法[4]和比较法等，其中比较法主要有差示扫描量热计(differential scanning calorimeter, DSC)法和激光闪光法等，国际上普遍使用合成蓝宝石(α-Al2O3)作为比热容标准物质。DSC法是目前用途最广，测量精度较高的方法之一[5]；激光闪光法拥有测量速度快和样品尺寸小、非接触测量等优点，是测量热扩散系数的标准方法[6]。闪光法系列导热仪通常声称测量材料热扩散系数偏差为±(2%～3%)，比热容偏差为±5%，重复性为2%～3%。由于闪光法加热激光脉冲时间极短，通常为20～1 000 μs，脉冲能量又较大，且存在非理想均匀光束的问题，实际试样上热损失会导致后表面最大温升的测量出现较大偏差，同时由于缺乏相应的技术规范和标准样品对测量准确性进行有效评定，实际闪光法导热仪测量比热容的结果可能更差[7]。

1961年Parker[8]率先提出了使用短脉冲激光闪光法测量试样热扩散系数和比热容，经过几十年发展，闪光法已经成为了热扩散系数测量研究最主要的方法之一[9]。然而，对使用连续激光加热来测量热物性参数的报道却极少，未见相应的理论模型和实验验证，使得激光加热法测量热物性参数的模式略显单调。因此，有必要研究一种准确性较高且考虑激光非均匀光束和热损失等影响的测量法，进一步提升通过激光加热法测量材料比热容和导热系数的能力，同时进一步提升激光加热法在极端条件下的测量能力。

本文提出了一种采用连续激光加热来测量金属材料比热容的方法，建立了有限尺寸试样在连续加热条件下的传热模型和准稳态测量模型；通过COMSOL数值模拟对测量模型和热损失的修正模型进行了验证；搭建实验装置，使用T2紫铜参考值进行系统参数的标定，在常温下对TC4钛合金、316 L不锈钢、45钢和7075铝合金试样的比热容进行了测量，并对测量结果进行了不确定度的评定。

2 测量模型

2.1 传统闪光法测量比热容

Parker等构建激光闪光法的理想一维传热模型为：功率密度均匀的激光完全覆盖照射在柱型试样的前表面，脉冲时间t0→0，试样为绝热边界，后表面的温升随时间t的变化情况为：

(1)

式中：L为试样厚度，mm；Q为试样前表面吸收的脉冲激光的热能，J/mm2；ρ为试样密度，kg/m3；α为试样热扩散系数，m2/s；cp为试样比定压热容(以下简称比热容)，J/(kg·K)。通过测量试样后表面温升达到最大值一半所需时间和试样厚度可以较容易获得试样的热扩散系数。

如今，激光闪光法研究发展相对较为完善，但其理想的测量模型存在一定的缺陷，忽略了激光脉冲时间、激光非均匀光束和边界热损失等情况的影响，实际测量时需要进行大量的修正，测量结果的不确定度较大。闪光法测量试样比热容的相对法测量模型为：

(2)

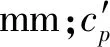
2.2 连续激光加热法测量比热容

激光闪光法测量试样的尺寸通常直径为10 mm或12.7 mm，厚度为2～5 mm，采用连续激光加热时热流很快就会达到热边界，对试样前表面加热可视为面热源加热，其三维瞬态导热微分方程为[10]：

(3)

式中：Φ为面热源，W/mm2；当Φ为定值，不考虑试样热物性参数随温度变化且试样边界绝热，温度在空间上的二次微分可以视为常数，且试样上的温升速率也可以视为常数。

假设加热激光光束均匀且光斑面积与试样前表面面积一致，试样为绝热边界，在试样厚度z轴方向上一维传热，根据Carslaw和Jaeger[11]建立恒定热流加热的温升模型，对式(3)积分可获得式(4)：

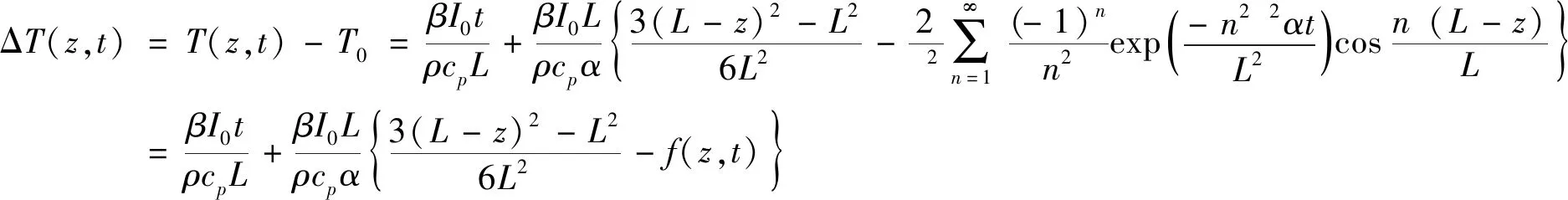
(4)

式中：z为试样上一点与前表面的距离，mm，L为试样的厚度，mm，其中z满足0≤z≤L；ΔT(z,t)为试样厚度方向上各点实时的温升，℃；β为试样前表面热吸收率，I0为激光功率密度，W/m2，βI0为试样前表面单位面积上实际吸收的热流；T0为试样初始温度，℃。对函数f(z,t)进行定值计算分析，当L=5 mm，α=10 mm2/s，f(z,t)随时间t的变化曲线见图1所示。

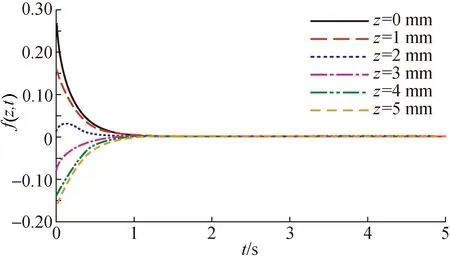
图1 f(z,t)随时间t的变化曲线Fig.1 The curves of function f(z,t) with time t

由图1可以看出，当时间t足够长时f(z,t)→0，且试样上任意0≤z≤L点都满足。因此，当t足够长时，试样上距离热源任意位置的温升可以表示为：

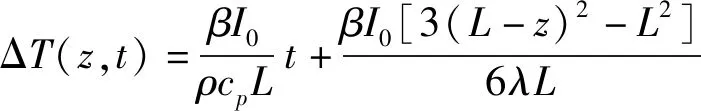
=mt+Td

(5)

式中：P0为激光输出功率，W;假设激光能量完全照射在试样前表面且照射光斑面积与试样前表面一致，则A为试样前表面面积，mm2；V为试样体积，mm3；M为试样质量，g；Td是与时间t无关，仅仅与空间相关的常数温度，℃；m为恒定激光功率加热足够长时间后试样上的温升速率；对有限尺寸且绝热边界的试样加热足够长时间时，试样上任意点都适用。

如此一来，可以认定在恒定激光热源连续加热足够长时间的情况下，试样上各点温升速率将趋于一致，并处于稳定状态。通过测量试样上任意一点的温升并进行线性拟合，可以获得连续激光加热法测量圆柱型试样比热容的解析公式：

(6)

根据式(6)，只需测量被测试样的质量和试样吸收激光的热功率，并通过测量试样上任意一点的温升随时间变化的情况就可以通过绝对法获得试样的比热容。然而，试样前表面实际吸收热功率βP0中热吸收率β较难直接获得，但可以通过已知比热容的试样进行标定，即其标定公式为：

(7)

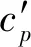
3 数值模拟和热损失修正

3.1 数值模拟

使用COMSOL Multiphysics 5.4多物理场仿真软件中固体传热物理场对上述通过连续激光加热来获得试样比热容的传热和测量模型进行验证。选取工业制造中较为常见的金属材料，常温下的导热系数、密度和比热容的参考数据[1,2]见表1，设定在20 ℃时各金属材料的物性参数进行仿真分析，且暂不考虑导热系数、密度和比热容随温度变化的情况。

表1 仿真金属材料参数Tab.1 Metal material parameters for simulation analysis

建立以坐标(0,0,0)为圆心直径为10 mm的试样受热面，试样厚度方向为z轴正方向；设置物理场控制网格，单元大小：细化；初始温度为293.15 K，固体传热方程设置为瞬态，其基本方程为：

(8)

式中：u为模型中平移运动子节点定义的速度场，m/s;T为温度的拉普拉斯算子；表示向量算子；k为材料导热系数，W/(m·K);Q为热源，W/m3；Qted为热弹性阻尼，W/m3。

设置边界热源为面加热源，热源公式为：

(9)

(10)

上述公式设置等效于加热激光为均匀光束，试样前表面吸收热功率密度为I1，W/mm2。当激光脉冲时间设置为20s时，试样上平均温升可以控制在10 ℃以内，且有足够长时间的温升曲线用于进一步的分析。

试样与样品架之间的接触热传导，试样表面产生的热辐射和空气对流均会对试样加热过程造成热损失，综合设置热损失的通量公式为：

q0=h(Text-Ts)

(11)

式中：h为试样表面综合传热系数，W/(m2·K)；Ts为试样表面平均温度，℃；Text为环境温度设置为293.15K。当h=0时，试样可以视为绝热边界；在气体强制对流情况下，固体表面传热系数h的范围一般为20～100W/(m2·K)[10]。当试样为圆柱型时，可将其简化为二维传热，见图2所示。

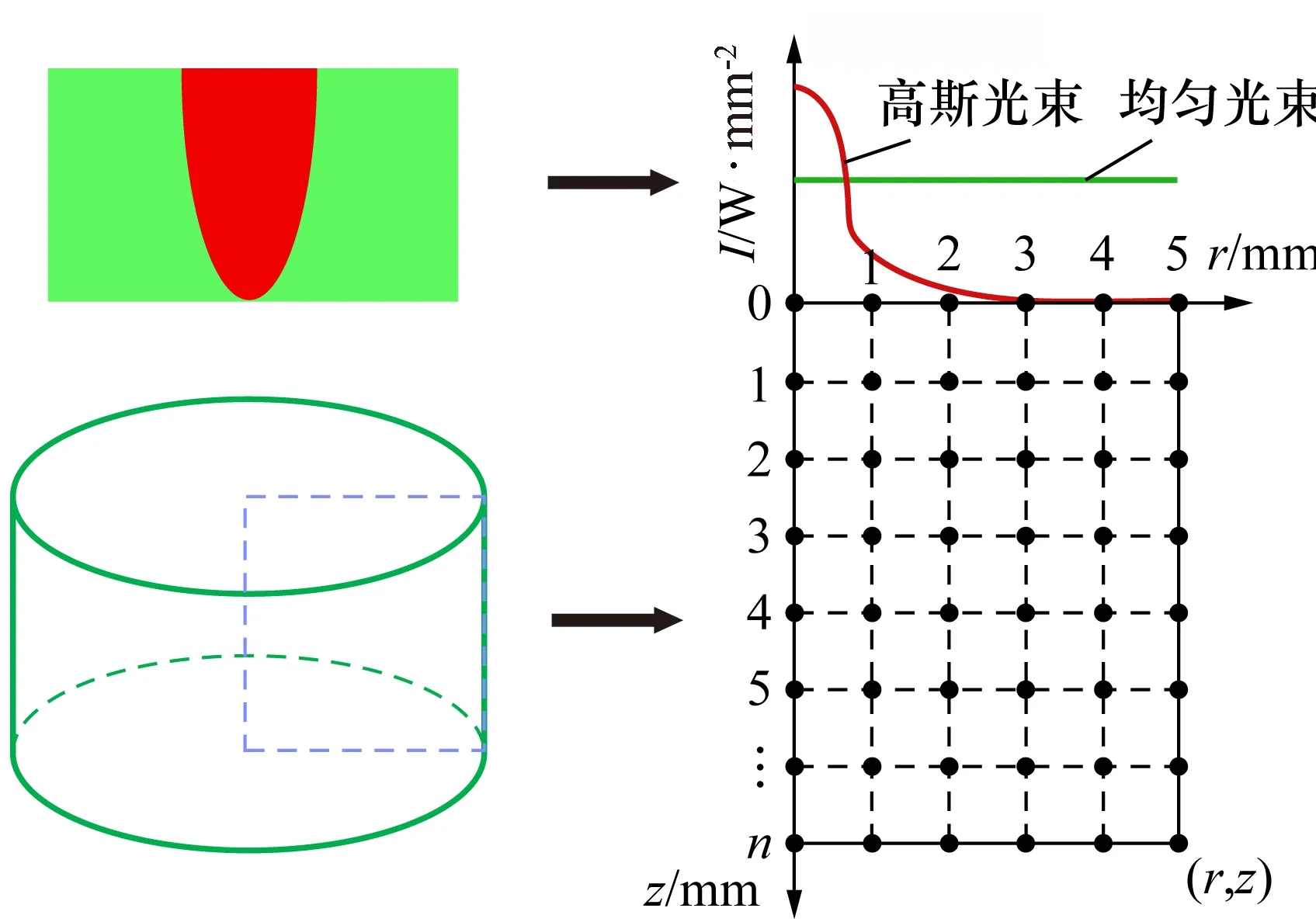
图2 简化二维传热分析示意图Fig.2 Simplified 2D heat transfer analysis diagram

当试样边界绝热，设置TC4钛合金试样厚度L=5 mm，7075铝合金试样厚度L=7 mm，在功率密度为I1的加热条件下可视为一维传热，各探针点仿真温升曲线见图3所示。

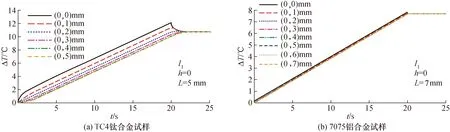
图3 绝热条件下均匀光束加热金属试样仿真温升曲线Fig.3 Simulated temperature rise curves of metal samples by uniform beam under adiabatic condition

由图3(a)TC4钛合金试样温升曲线可以看出，在连续加热一定时间后，各探针点的温升呈平行上升即温升速率趋于一致；图(b)中，7075铝合金试样上各探针点的温升几乎重合，即使试样厚度比TC4钛合金试样厚2 mm，但探针点之间温差更小。图3中金属试样的温升曲线验证了式(5)的合理性，当试样导热系数越大时，试样温升速率越快趋于稳定，试样上各探针点的温差也越小。

通常连续激光器输出激光并非理想的均匀光束，而是高斯光束，当试样前表面实际热吸收功率为0.5 W时，其光斑功率密度分布[12]式为：

(12)

式中：I2为试样前表面实际吸收功率密度分布，W/mm2；r为距离光斑中心的距离，mm；R为激光光斑半径，mm。高斯光束在r≤R范围内约占总能量的86.5%。设置高斯光束半径为R=1.25 mm，当r=3 mm时，功率密度为2.023 W/mm2，高斯光束在范围内占激光总能量的99.999%，即当试样直径大于6 mm时，可以保证激光的总能量均照射于试样前表面。

当试样边界绝热，设置316 L试样厚度L=5 mm，T2紫铜试样厚度L=7 mm，在功率密度I2的加热条件下各探针点仿真温升曲线见图4所示。由图4试样温升曲线可以看出，在连续加热一定时间后，各探针点的温升仍呈平行上升即温升速率趋于一致；由于高斯光束并非理想的均匀光束，其对试样前表面加热时中心功率较为集中，从而产生了径向上的温度梯度，此时试样上也并非理想的一维轴向传热，试样上各探针点的温差也更为明显。

图4 绝热条件下高斯光束加热金属试样仿真温升曲线Fig.4 Simulated temperature rise curves of metal samples by Gaussian beam under adiabatic condition

通过仿真结果可知，当连续高斯光束激光总能量均照射在有限厚度试样前表面，且边界绝热，加热时间足够长时，试样上各点的温升仍满足公式：

ΔT(r,z,t)=mt+Td(r,z)

(13)

式中：m为加热时间足够长时，试样上的温升速率；Td(r,z)是与空间坐标r，z相关的常数温度，℃。

设置TC4钛合金和316 L不锈钢试样上探针点(0,0,2) mm；7075铝合金和T2紫铜试样上探针点(0,0,4) mm，在不同综合传热系数下各探针点的仿真温升速率曲线见图5所示。在h=0即试样为绝热边界，设置功率密度I1和I2加热时，由于试样吸收热功率一致，稳定状态时温升速率曲线重叠，通过提取稳定状态时为定值的温升速率m，在已知试样实际热吸收功率的情况下，通过式(6)可以较为容易获得试样比热容。当h=20，50，80 W/(m2·K)即试样存在热损失时，探针点的仿真温升速率不为定值，但在一定时间后温升速率呈现为稳定趋势减小，未经修正的计算结果比理论值偏大2%甚至超过30%。

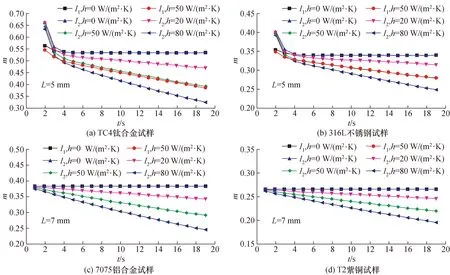
图5 各金属试样在不同传热系数下的温升速率仿真结果Fig.5 Simulation results of temperature rise rate of different metal samples under different heat transfer coefficients

3.2 热损失修正

考虑到仿真设置的综合热损失通量公式(11)，当试样表面综合传热系数h为定值，试样初始温度T0与环境温度Text一致，存在热损失情况下，试样上各点位的温升在加热足够长时间后可以表示为：

(14)

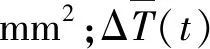
(15)

式中：A≤0，取决于试样表面综合传热系数h的大小；B≈βP0/(cpM)；C为较小量常数，且当t=0时，C→0，可以忽略。将式(15)代入式(14)，可以进一步表示为：

(16)

求导可以得到试样温升速率变化公式：

(17)

由图5不难发现，当h→0，m=βP0/(cpM)为恒定值，当h变大，仿真的温升速率近似线性地减小，热损失情况下的温升速率可以简化描述为：

m(t)=nt+mc

(18)

式中：n为温升速率随时间减小系数；mc为修正后的温升速率。选定合适的温升速率数据段是修正的关键，温升速率达到准稳定状态，并需要选取足够长的数据段进行处理，取如下时间数据段进行拟合修正：

(19)

对h=20，50，80 W/(m2·K)时，使用公式(18)对试样上各探针点温升速率进行修正后，通过式(6)计算获得的比热容与仿真设置值的偏差见图6所示。

由图6可以看出，在设置功率密度I2加热时，当金属试样表面综合传热系数h越大，各试样修正后计算结果与仿真设置值的偏差也就越大，同时试样导热系数越大，所受到表面综合传热系数h的影响也就越小；由图6(a)和图6(b)不难发现，当金属试样导热系数越小，试样上各探针点温升经修正后计算结果差异也越大，试样边界温升受热损失影响较大，试样中心位置受热损失影响较小。

图6 各金属试样修正计算的比热容与理论值的偏差Fig.6 Deviation between calculated specific heat capacity and theoretical value after correction for each metal sample

当探针点满足r≤2 mm和2 mm≤z≤L-2 mm时，各探针点的温升速率通过式(18)进行修正，并使用修正后的温升速率mc代入式(6)计算比热容，计算结果与表1中理论值偏差见表2。

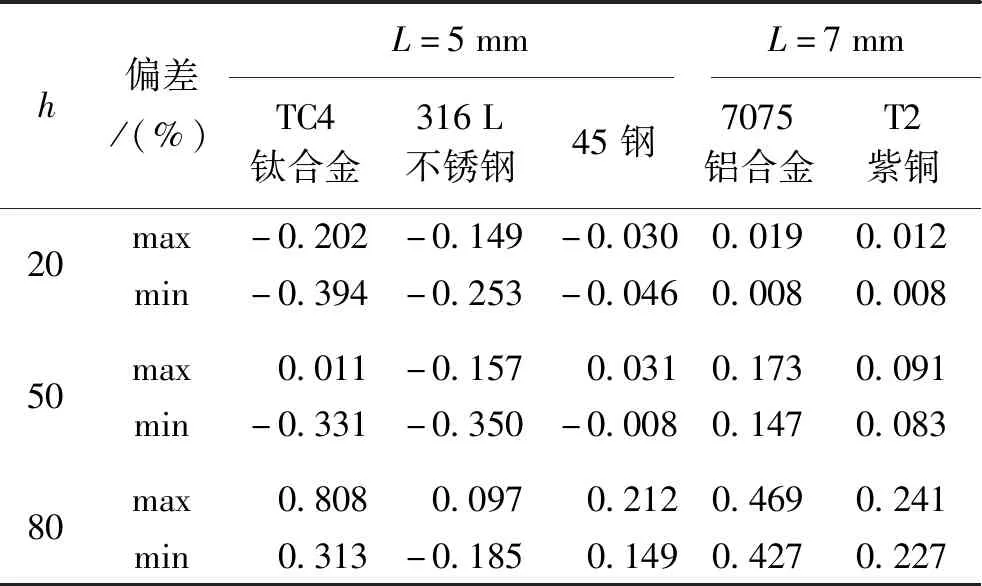
表2 修正后计算比热容与理论值偏差Tab.2 Deviation between calculated specific heat capacity and theoretical value after correction

由计算结果可以看出，经修正后计算结果与表1所提供的理论值偏差小于±0.81%，当h≤50 W/(m2·K)时，经修正后的计算结果与理论值偏差小于±0.39%。通过仿真验证了本文所提出的热损失修正公式(18)及数据段选择范围(式(19))的合理性；但修正模型需要尽可能测量试样内部的温升来减小边界热损失造成的影响，这对实际测量提出了较高的要求，尚需要通过实验来进一步验证所提出热损失修正模型的可靠性和实用性。

4 实验系统及样品处理

4.1 实验系统

实验系统主要分为激光热源、被测试样、测温设备和控制、测量和分析软件等，主要装置见图7所示。热源激光使用的是型号Millennia Prime Laser 10sJ波长为532 nm的连续激光器，同激光闪光法所使用的极短脉冲激光器存在本质差异，其最大输出功率可达10 W，稳定性优于±1%，自带输出功率显示器；其高斯光束直径标称为2.3 mm±10%，使用光束质量分析仪BP209-VIS/M对其光束直径进行测量，x、y轴方向宽度分别为2 402.4 μm和 2 433.0 μm。

图7 实验装置示意图Fig.7 Diagram of experimental equipment

测控程序基于LabVIEW编写，主要实现功能有：控制激光器快门开关，设置保持时间，实验测量中激光加热脉冲时间通常设置为20 s；实时读取34420A对Pt100测量的阻值并换算成温度，实现对有机玻璃罩中温度的监控；实时读取3458A测量极细K型热电偶的输出电压随时间的变化曲线，使用Pt100所测环境温度进行冷端补偿；并在激光器快门打开同时进行数据记录，待1次加热测量结束后换算成温升曲线并进行数据处理和分析；通过对已知比热容试样测量曲线分析处理，实现对系统参数进行标定等。

4.2 样品处理

为测量金属试样内部温升，采用打微孔的方式在金属试样上进行打孔，打孔位置示意图见图8所示，其中微孔直径d1,2=(0.22±0.02) mm，图8(a)中微孔深l1=(5±0.2) mm，图8(b)中微孔深h2=(3±0.2) mm。使用铠装后直径为0.15 mm的K型热电偶直接对试样内部进行测温，可以有效减小因表面接触测温存在热阻和空气对流导致温度测量的偏差。

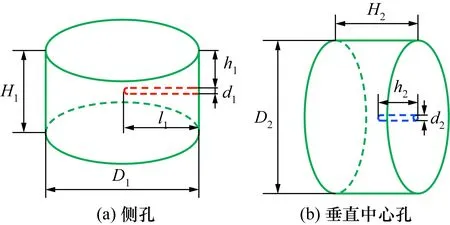
图8 试样打孔位置示意图Fig.8 Diagrams of punching position of samples

使用0.1 mg精度的FA100B型电子天平和分辨率为0.01 mm的游标卡尺对待测金属试样的质量和规格进行测量；并使用ZB603C型珠宝天平和密度测量组件，以无水乙醇作为辅助液体，通过浮力法对各试样密度进行测量，各试样密度与表1中参考密度的相对偏差详见表3。各金属试样密度的测量结果与参考数据相对偏差为 -0.78%～0.09%，实际加工的金属试样材质、状态和热处理等与数据手册上的材质存在一定的差异，且浮力法测量过程中因操作不当，液体温度变化，试样打孔等都会导致密度测量结果存在一定偏差。

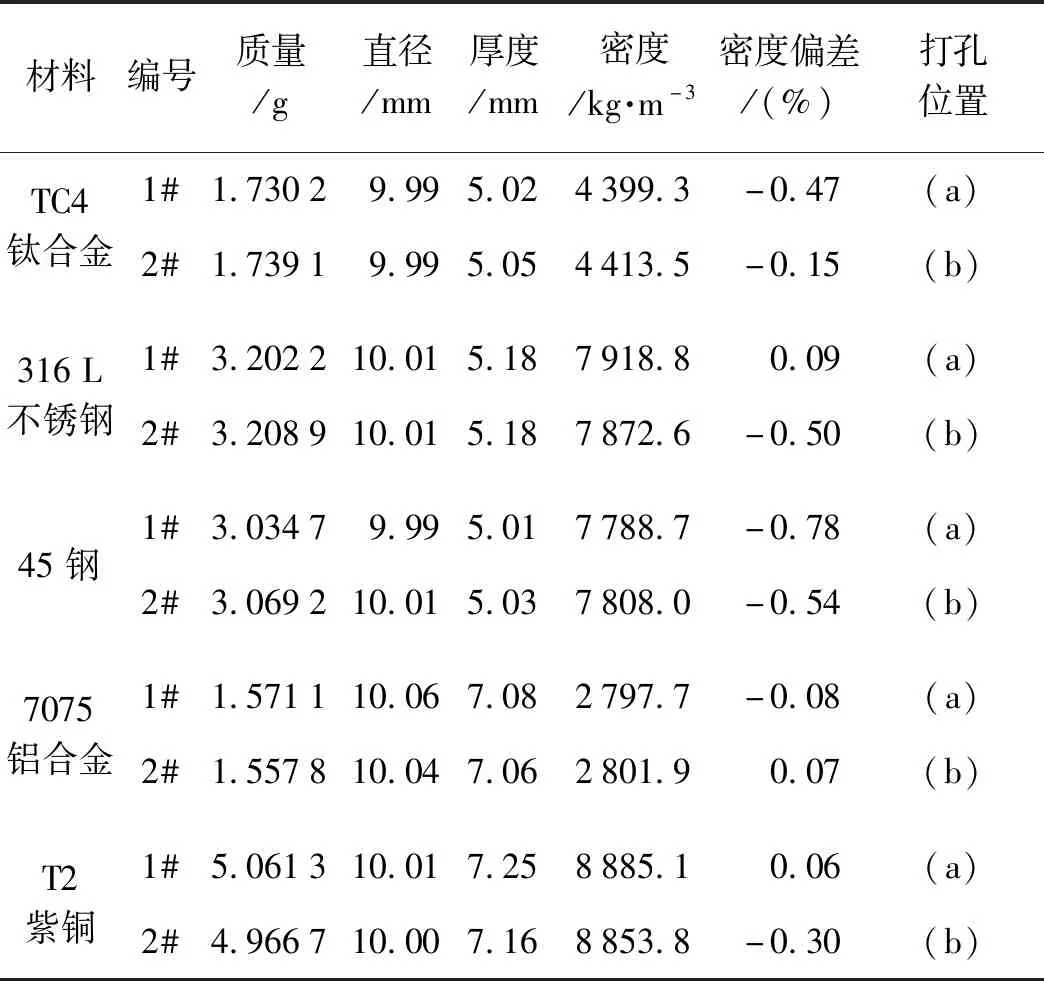
表3 待测金属试样尺寸、质量参数Tab.3 Size and quality parameters of metal samples

对待测金属试样受热面使用GRAPHIT 33石墨涂层剂进行均匀喷涂，重复喷涂2次，干燥后观察表面是否较为均匀、表面无明显反射和折射，喷涂石墨涂层后各试样质量仅增加0.9～1.7 mg，对金属试样质量测量的影响小于0.10%，在测量计算时可以忽略不计并认定为是系统偏差，在不确定度评定中增大质量测量引入的不确定度。试样喷涂石墨前、后实物见图9所示，从左往右分别为T2紫铜、7075铝合金、45钢、316 L不锈钢和TC4钛合金。

图9 试样喷涂石墨前、后实物图Fig.9 Photographs of samples before and after spraying graphite

5 测量结果及其不确定度评定

5.1 系统标定

当设置激光器输出功率为0.5 W时，功率显示器所显示功率为0.52 W，而使用S425C-L型功率计测量的功率为0.58 W，重复测量6次的曲线见图10所示。

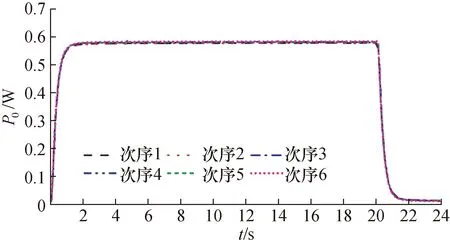
图10 功率计测量激光功率曲线Fig.10 Laser power curve measured by power meter

由于S425C-L型功率计测量不确定度为±5%，直接使用功率计测量值会引入较大的不确定度，同时试样前表面热吸率β无法直接获得，导致式(6)无法直接用于对试样比热容进行测量。对此，采用图9所示方法，在相同条件下对试样前表面喷涂石墨涂层剂，确保各试样前表面热吸率β尽可能一致；由图10激光功率重复测量曲线可知，待激光功率稳定后波动小于±1%，重复性也优于1%，其稳定性可以直接表征于测量结果的重复性；在测量各试样时激光器输出功率P0恒定，则可通过式(7)对试样前表面实际吸收功率βP0进行标定，避免直接测量获得各参数引入较大的不确定度。

国际上通常使用蓝宝石和高纯铜作为比热容的标准物质[13]，有关纯铜的比热容测量报道较多[14～18]，测量结果可靠性也较高；由仿真结果可知，紫铜样品经热损失修正后偏差较小，当h≤80 W/(m2·K)时，经修正后偏差小于±0.25%。本文使用T2紫铜(工业纯铜，含铜量≥99.90%)作为标定样品，部分文献及数据手册报道纯铜样品的比热容结果见图11所示。

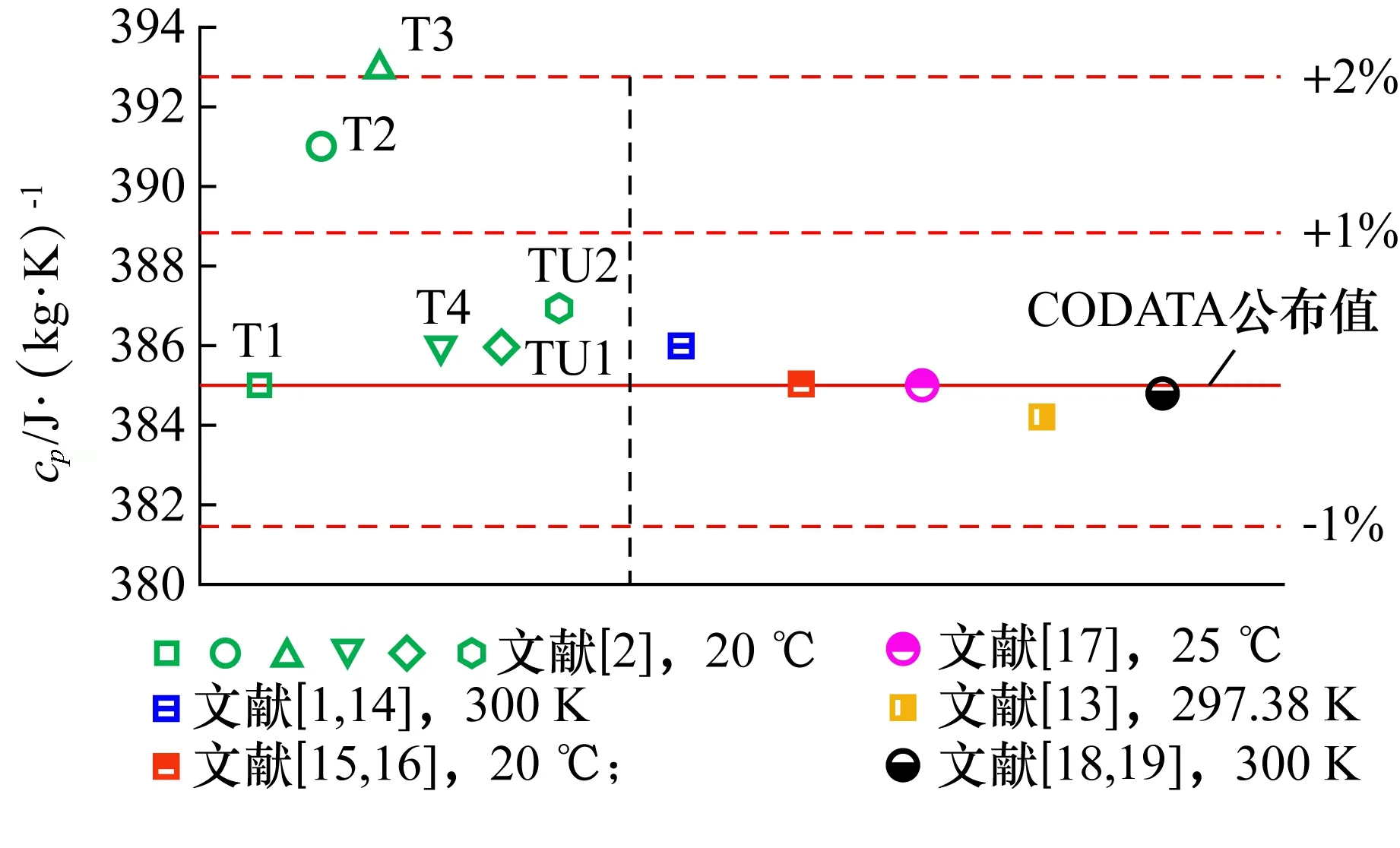
图11 文献报道的紫铜比热容Fig.11 Specific heat capacity of copper reported in literature

文献[2]中报道T2紫铜比热容与其它文献报道纯铜偏差约为1.56%；文献[15,16]报道不同牌号纯铜的比热容基本一致，牌号为T2/C11000紫铜在20 ℃时的比热容为385 J/(kg·K)，与文献[13]中报道CODATA公布的纯铜比热容数据较为接近；基本可以认定标定所用T2紫铜试样在20 ℃时的比热容为385 J/(kg·K)，偏差在±2%以内，远小于直接测量激光功率和试样表面热吸收率引入的不确定度。使用表3中T2紫铜1#、2#试样测量结果进行系统标定，温升速率拟合修正处理见图12，重复测量的修正结果见表4所示。

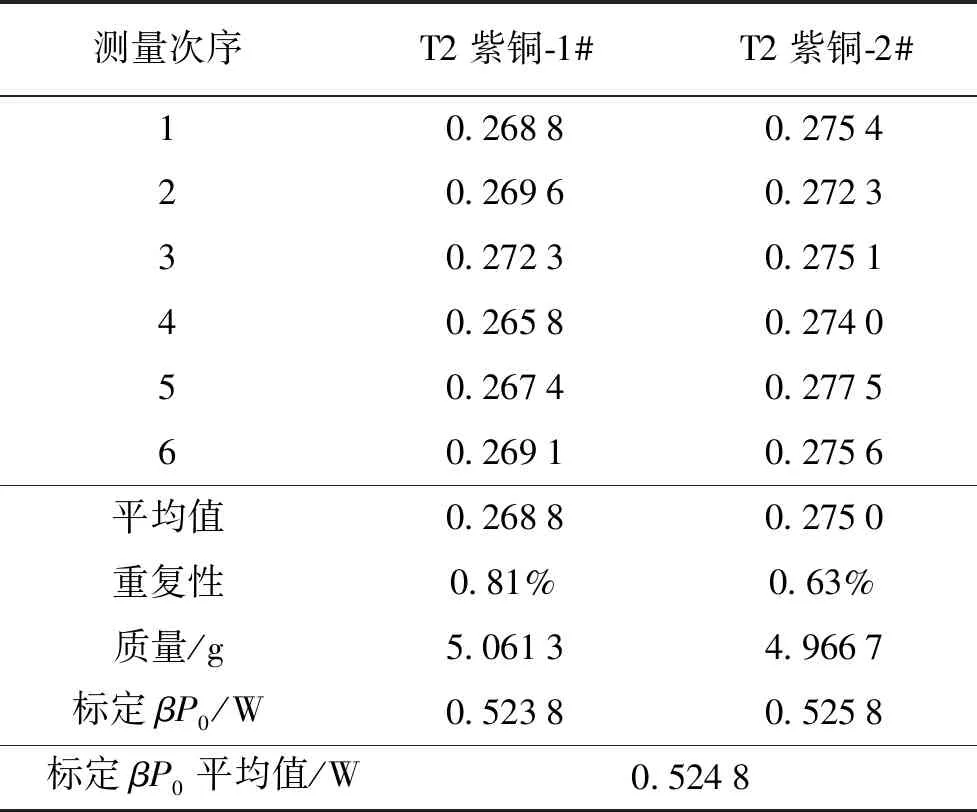
表4 T2紫铜试样测量温升速率mc的修正结果Tab.4 Correction results of temperature rise rate mc of copper T2 samples

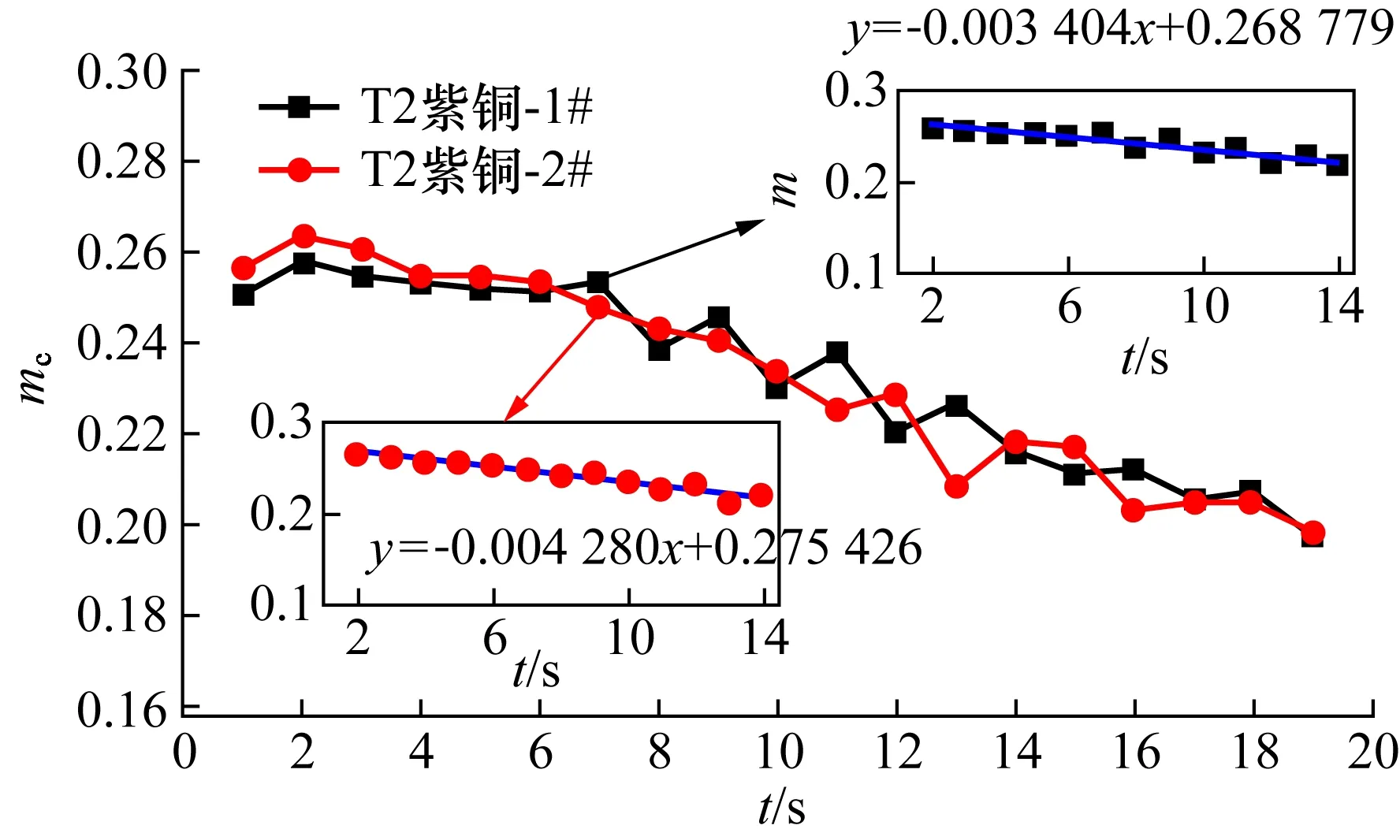
图12 T2紫铜样品温升速率拟合修正Fig.12 Correction of temperature rise rate of copper T2 samples

对T2紫铜1#、2#样品分别重复测量6次，取修正后温升速率的平均值进行系统标定，测量重复性分别为0.81%和0.63%，两者平均值偏差为0.38%，有较好的重复性，标定βP0平均值为0.524 8 W，高于激光器设置和显示功率，与功率计显示功率比值约为0.9，即经喷涂石墨后金属试样表面热吸收率β≈0.9。

5.2 测量结果

使用T2紫铜试样对图7所示实验室搭建的测量系统进行试样前表面实际吸收功率βP0参数标定后，在相同条件下，对图9中喷涂石墨后的其余各金属试样在(20±2) ℃环境温度下，进行比热容的测量，并重复测量6次，测量结果见表5所示。由表5可知各金属试样比热容测量重复性优于0.91%；同一材质不同编号试样测量结果平均值的偏差小于0.43%，说明试样打孔位置不同对测量结果无较明显影响。

各金属试样测量结果平均值与文献参考值比较情况见图13所示，与表1中参考数据偏差小于±1.5%，与数据手册报道值偏差均在±3.1%以内。通过实验测量结果验证了连续激光加热法对金属材料的比热容测量具有较高的准确性和重复性，测量和修正模型有较好的可靠性。

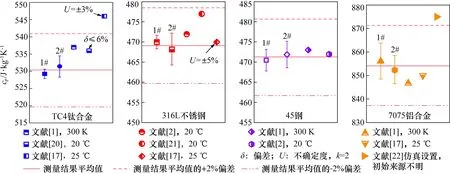
图13 各金属试样比热容测量结果与文献报道值比较情况Fig.13 Comparison of specific heat capacity of each metal sample with that reported in literature

5.3 测量不确定度评定

实验搭建的金属试样比热容的测量装置，采用的是相对法测量模型，结合式(6)、式(7)其测量模型为：

(20)

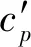
A类不确定度由实验测量重复性引入[23]，由表5重复测量6次实验结果可知，标定样品最大相对标准偏差为0.81%，被测样品最大相对标准偏差为0.91%，按3次测量的平均值作为测量结果，则由标定和被测样品测量重复性引入的标准不确定度分别为：

表5 金属试样比热容的测量结果Tab.5 Measurement results of specific heat capacity of metal samples J·(kg·K)-1

u11=0.81%/1.732=0.468%，

u21=0.91%/1.732=0.525%。

B类评定中，根据图11中比较认定结果可知，标定所使用的T2紫铜试样比热容偏差在±2%以内，按均匀分布，则标定样品定值偏差引入的标准不确定度为u12=2%÷1.732=1.155%。试样质量测量偏差主要由电子天平的不确定度、打孔损失质量以及喷涂石墨层导致，其中打孔和喷涂石墨层导致试样质量最大偏差分别为0.05%和0.10%，总体引入的标准不确定度为0.25%，即由标定和被测样品质量测量偏差引入的标准不确定度为u13=u22=0.25%。温升测量偏差主要由热电偶以及3458A等测量仪器不确定度导致，综合评估，由标定和被测样品测量温升引入标准不确定度为u14=u23=0.3%。根据仿真分析结果可知，标定样品经热损失修正后的最大偏差为0.241%，被测样品经热损失修正后的最大偏差为0.808%，按均匀分布，由标定和被测样品热损失修正模型引入标准不确定度为u15=0.241%÷1.732=0.139%，u24=0.808%÷1.732=0.467%。温升速率修正拟合偏差主要由选取拟合数据时间段和拟合间隔导致，同时受测量环境干扰造成的随机误差所影响，评估综合偏差在±1%以内，按均匀分布，由标定和被测样品温升速率修正拟合偏差引入标准不确定度为u16=u25=0.577%。根据文献数据手册参考值比热容与温度线性拟合，10 ℃以内比热容偏差在0.2%以内，则由标定和被测样品比热容与温度线性拟合偏差引入标准不确定度为u17=u26=0.2%。评估由被测样品与标定样品表面喷涂石墨差异引入标准不确定度u27=0.5%。各相对标准不确定度分量ui见表6所示。

表6 测量不确定度评定表Tab.6 Evaluation table of measurement uncertainty

综合评定本文所搭建实验装置测量金属材料比热容的相对扩展不确定度U=2uc=3.66%(k=2)。

6 结 论

通过使用COMSOL数值模拟和实验验证了所提出基于连续激光加热法可以通过系统标定来测量获得金属材料的比热容，建立的有限尺寸试样在连续加热条件下的传热和测量模型以及热损失修正模型具有较好的可靠性。搭建实验系统，在常温下，使用T2紫铜对参数进行标定后测量了TC4钛合金等4种金属材料，各金属试样测量结果平均值与表1中参考值偏差小于±1.5%，与数据手册报道值偏差均在±3.1%以内，测量相对扩展不确定为3.66%，获得了较好的测量结果。

同激光闪光法相比，连续激光加热法的传热模型属于准稳态，准确性更高，热损失修正较为简单可靠；对于测温设备响应速度和采样速率的要求相对较低，可以大大减小测温端的设置成本。然而，由于本文所使用实验装置需要对金属试样打孔并不适用于大批量的实际测量需求，因此，仍需进一步研究采用辐射测温法对加热试样进行非接触测量的实验验证，研究适用于连续激光加热条件下导热系数的测量解析和修正模型，从而获得更加完善的热性能测量能力。