基于深度迁移学习的时变拓扑下电力系统状态估计
2021-12-29臧海祥郭镜玮黄蔓云卫志农孙国强俞文帅
臧海祥,郭镜玮,黄蔓云,卫志农,孙国强,俞文帅
(河海大学能源与电气学院,江苏省南京市 211100)
0 引言
电力系统状态估计在电力系统规划和运行中具有重要的意义[1-2],可以为实时调度以及后续一系列电力系统高级应用和分析提供可靠的数据库[3]。目前,基于加权最小二乘(weighted least square,WLS)的状态估计已被广泛应用于实际电力系统中,WLS的估计结果具有方差最小且无偏的统计特性。在理想条件下,该算法是最优的状态估计方法[4]。由于电网结构、运行工况和现场环境等因素的影响,量测系统中不可避免地存在一定比例的坏数据,但WLS属于L2 范数估计,该方法会将残差放大,当量测系统存在一定比例坏数据时,WLS 易出现不收敛的情况[5-6]。
针对上述问题,人们将研究重心聚焦到抗差估计算法中,其中最常见的是基于加权最小绝对值(weighted least absolute value,WLAV)状态估计[7]。WLAV 属于L1 范数估计,利用非二次估计准则的优势,解决了因加权平方和导致残差放大的问题,将估计精度控制在既定范围之内。该算法通常利用原对偶内点法进行求解。除此之外,文献[8-9]提出的M估计通过降权措施,在计算速度、收敛性以及鲁棒性上得到了进一步提升。文献[10]提出的指数型目标函数估计适用于任何概率分布形式的量测系统,能够自动排除坏数据对估计性能的影响,但是该方法会使状态量陷入局部最优。
然而,上述传统状态估计算法受系统规模和硬件水平影响较大,尤其在大系统中估计时间较长,不满足状态估计实时性的要求[11-12]。针对该问题,文献[13]采用粒子群算法优化极限学习机方法对锂电池荷电状态进行估算,提高了荷电状态估算的精度和效率。文献[14]采用神经网络进行大电网状态估计,提高了状态估计的鲁棒性和实时性。文献[15]将脉冲神经网络应用于配电网状态估计的伪量测建模。但是在实际电网运行过程中,系统拓扑是时变的[16],而且历史数据库中难以包含所有拓扑的海量数据。因此,经常出现过拟合的情况,从而导致状态估计结果不准确[17-18]。鉴于此,可以利用原拓扑下海量的历史数据来弥补新拓扑样本少的问题[19]。
迁移学习(transfer learning,TL)作为联系2 个不同域之间的重要方法,其核心是通过源域海量的数据学习相关知识并将其迁移到目标域以改善目标任务的学习性能[20-21]。利用迁移学习可有效挖掘2 种域之间的潜在联系以及提高数据驱动状态估计模型的泛化性能。同时,离线阶段中仅需要对模型全连接层微调,使离线训练效率也有明显提升。
本文基于深度迁移学习提出一种针对拓扑时变情况的状态估计方法。该方法分为离线训练和在线应用2 个阶段。对于离线训练阶段,首先,合理选择一种拓扑作为基准拓扑(源域);其次,利用源域历史量测和状态量作为预训练模型的输入和输出并进行离线训练;最后,以预训练模型为基础,通过历史数据库中少量新拓扑的样本进行模型微调。对于在线应用阶段,首先,采集新拓扑下当前断面的量测生数据;其次,将该数据输入离线训练阶段得到的模型;最后,获取该断面最接近系统真实状态的估计值。通过在IEEE 标准系统和某实际省网进行的试验表明,本文方法较传统的WLS 和WLAV 以及深度神经网络(deep neural network,DNN)进行小样本训练有2 个方面的优势:①该方法的估计性能优于对比方法;②估计时间小于WLS 和WLAV。
1 深度迁移学习算法基本原理
1.1 深度学习基本原理
深度学习核心功能是根据输入的数据进行分类或者回归[22]。与浅层学习相比,深度学习组合若干低层次特征,从而挖掘高维数据的分布形式,这种组合方式可以让深度学习更好地适应较为复杂的函数表达[23]。与传统机器学习算法相比,深度学习最大的特点是端到端(end-to-end)的学习,在进行学习之前,无须进行特征提取等操作,可以通过深层次的网络模型自动从原始数据中提取有用的特征[22]。将深度学习应用在电力系统中可以有效挖掘历史数据特征,并且可以弥补传统机器学习中存在的函数表达能力不足的缺陷[23-24]。
1.2 迁移学习基本原理
迁移学习的核心是对一组数据集特征的深层挖掘,提取其相关知识并将其运用到其他未知且相似的领域中[25]。迁移学习具有较强的自适应性,与其他机器学习相比,迁移学习有3 点优势:①训练和测试数据可以服从不同分布;②无须大量带标签数据;③模型可以在不同任务之间迁移[26]。
在迁移学习中,设下标S 和T 分别代表源任务和目标任务,DS和DT分别为源域和目标域,利用特征向量空间X和概率分布函数P(X)构成对应的领域,即[25-26]:

设Ys和Yt分别为源域和目标域的标签向量空间,fs和ft分别为源域和目标域的映射函数,则源域和目标域内的任务Ts和Tt可分别描述为:

假设源域与目标域的特征分布相同,但标签空间不同,则迁移学习的目标是使学习映射函数ft:Xt→Xs在DT上的期望误差最小,并满足Xt=Xs、Yt=Ys和P(Yt|Xt)≠P(Ys|Xs)。
本文在源域模型训练中使用卷积神经网络(convolutional neural network,CNN),利用网络的特征学习能力,进行2 个领域的知识迁移。具体知识迁移流程示意图如附录A 图A1 所示。
2 基于迁移学习的状态估计
2.1 预训练模型
在一个系统主体结构不变的情况下,增加或减少某几条支路在数据的表现上依然有极大的相似性,因此,可以将原拓扑的数据迁移到新拓扑中。具体迁移过程如图1 所示。
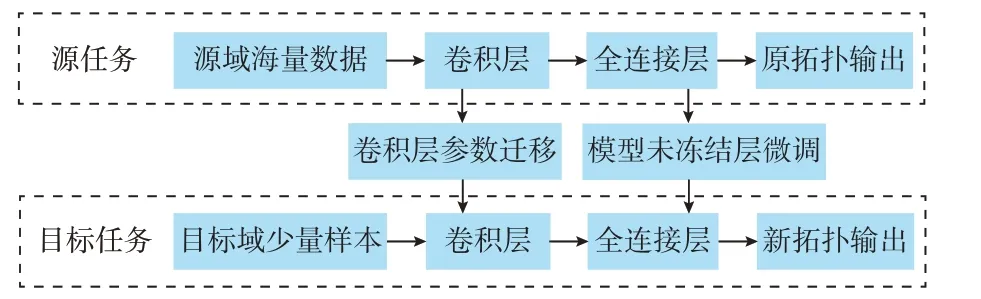
图1 模型迁移过程Fig.1 Model migration process
本文预训练模型使用CNN。其结构图如附录A 图A2 所示。CNN 包括卷积层、激活层和池化层[27]。卷积层采用局部连接和权重共享的方式,使得卷积层与下一层的连接数显著减少。CNN 输出的结果是数据的特征向量,因此在最后一层池化层后要接入全连接层。
在前向传导阶段,第l层第p个的净输入(指没有经过非线性激活函数的净活性值)z(l,p)为第l-1 层第p个活性值a(l-1,p)与卷积核ω(l,p)∈RK的卷积,即[27]:

式中:卷积核ω(l,p)∈RK为可学习的权重向量,其中RK为K维实数向量空间;b(l,p)为可学习的偏置;y(l,p)为第l层第p个神经元激活后的输出;f(·)为非线性激活函数,设x为来自上一层神经网络的输入向量,一般用ReLU 函数表示,如式(4)所示。

在反向传播过程中,首先,将实际结果与预期结果的误差按前向传播路径逐层返回,计算出每一层的误差。然后,进行权值更新。最后,得出满足要求的结果。
本文选用CNN 作为基础拓扑数据的特征提取器,再将预训练模型卷积层冻结,保存和加载其权重和参数,利用历史数据库中新拓扑的少量样本微调模型未冻结部分得到新拓扑的神经网络。此方法既可以解决新拓扑下出现的小样本问题,也可以提高估计效率以及数据驱动状态估计模型的泛化能力。
2.2 模型训练与数据预处理
本文采用电压幅值和相角并行估计的方式进行模型离线训练。在源域中,通过分析数据的时序特性,利用原拓扑海量历史数据进行基础模型的预训练并将其作为特征提取器。在拓扑变化时,分析2 种拓扑之间的潜在联系,在基础拓扑进行模型微调,最终得到新拓扑下的数据驱动状态估计模型。
通常,状态估计方法得到的估计结果是节点复电压。但从数据本身出发,节点相角是一个相对值,因此,利用数据驱动对节点电压相角进行状态估计时,会因数据之间缺少物理联系而导致估计精度不高,但对于潮流断面的计算,相角差的准确估计更有意义。为了能够体现数据之间的电气联系,并更好地体现出最终潮流计算的准确性,本文将支路相角差代替节点相角作为待估计量。这样可以加强数据之间的关联性,从而提高数据驱动状态估计的估计性能。具体转换公式为:

式中:φ为节点电压相角估计向量;Δφ为支路相角差估计向量;D为关联矩阵。
本文量测与状态变量之间的函数关系为:

式中:kij为支路ij变压器非标准变比;φij为支路ij的相角差向量;Gij和Bij分别为节点i至节点j导纳矩阵中的实部和虚部所形成的矩阵。
为了减少数据量纲对预训练网络的影响以及避免网络训练时出现过拟合现象,源域模型进行训练前将数据进行归一化处理。具体公式为:
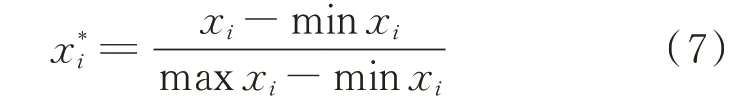
为了使数据驱动状态估计模型适应实际系统的各种工况,提升其抗差性,本文在训练集中加入随机混合高斯误差,使数据驱动状态估计模型具有良好的鲁棒性。
2.3 算法流程
本文提出的基于深度迁移学习状态估计方法,能够有效挖掘和提取历史数据以及2 种不同域之间的潜在关联。在离线训练阶段,首先,通过原拓扑的历史数据以及添加随机噪声训练基础神经网络;其次,利用少量新拓扑历史数据对基础网络进行微调。在线估计阶段,采集新拓扑的实时量测,输入新拓扑模型即可获取当前断面的快速状态估计结果。具体流程图如图2 所示。
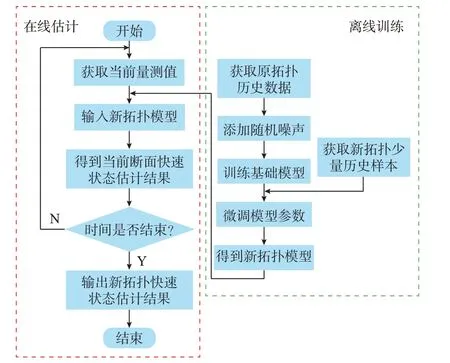
图2 深度迁移学习状态估计流程图Fig.2 Flow chart of state estimation for deep transfer learning
3 算例测试分析
3.1 测试系统与模型调优
为验证本文方法的有效性,将所提方法在IEEE 118 节点系统和某实际省级电网中进行试验。
在源域中,首先,利用省级电网实际运行数据得到负荷曲线,并得到原拓扑下的多断面量测。其次,利用WLAV 进行多断面状态估计获取相应的状态量,将得到的量测与对应状态量按照训练集与测试集数量的比例为15∶1 的原则进行数据分配并进行网络训练。
在目标域中,假设拓扑变化后的数据量只有5 个断面,那么可以在源域模型的基础上进行微调,从而得到适应于新拓扑下的状态估计模型。
本文算法基于Python 中的Keras 模块实现。模型调优主要包括网络层数和神经元个数等。模型迁移的调优主要包括冻结层个数。本文仅展示部分模型估计过程以及模型迁移估计结果。不同卷积层数和冻结层数的估计结果如表1 和表2 所示。
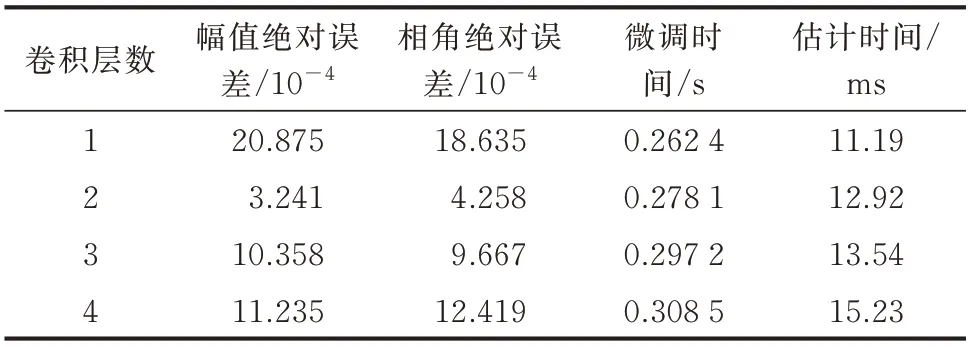
表1 不同卷积层数的估计结果Table 1 Estimation results for different number of convolution layers

表2 不同冻结层数的估计结果Table 2 Estimation results for different number of frozen layers
由表1 和表2 可以看出,CNN 的层数为2,冻结层数为4,即冻结全部的卷积层,微调模型剩余的全连接层。此时的估计精度和估计效率达到最优。其余估计过程、整体基础模型参数以及各层含义见附录B。
3.2 IEEE 118 节点系统测试
3.2.1 估计精度测试
本文在理想条件下测试该方法在IEEE 118 节点系统的估计精度,其中,训练集和测试集的收敛曲线见附录B 图B1 和图B2。为了更好地表现出拓扑前后各个电气量的变化,本文利用支路1 拓扑变化前后的首端有功功率和首端无功功率进行展示,具体如附录C 图C1 所示。
从附录C 图C1 可以看出,经过模型迁移后,本文方法在仅含高斯白噪声情况下能够准确估计系统状态。在经过一定的数据积累进行模型微调后,新拓扑模型依然适用。
为了能让各个算法之间的估计结果更直观地表现出来,对测试集数据进行状态估计计算并与真值进行比较得到最大绝对误差值。因为小样本直接训练的DNN 估计精度与其他方法有数量级的差距,所以本文采用对数形式进行成果展示,状态估计的估计精度合格线εk,max在对数值为3 的位置。其计算公式为:

表3 为不同算法下节点电压幅值、支路相角差、支路首端有功功率和支路首端无功功率的最大绝对误差的标幺值。从表3 可以看出,本文方法所得的支路相角差和节点电压幅值误差较WLS 分别降低了48.17% 和41.36%,与WLAV 相比降低了52.71%和43.6%,其估计误差低于上述2 种传统的物理模型驱动状态估计。而由小样本直接训练得到的DNN 估计精度明显达不到状态估计的精度要求。

表3 IEEE 118 节点系统的状态估计误差对比Table 3 Comparison of state estimation errors for IEEE118-bus system
3.2.2 鲁棒性测试
为了让该估计方法能更好地适应电力系统各种工况。本节在历史样本中随机选择部分量测添加混合高斯误差构成含噪声的训练样本,以此测试该算法的鲁棒性,添加的坏数据包括功率量测和电压幅值量测。
图3 为不同方法在添加20%混合高斯误差后的支路首端功率误差。

图3 IEEE 118 节点系统含坏数据状态估计精度Fig.3 Accuracy of state estimation for IEEE 118-bus system with bad data
从图3 可以看出,当量测系统存在不良数据时,本文方法计算出的支路潮流精度较其他方法有所提高,其中,由小样本直接训练得到的DNN 估计精度明显达不到状态估计既定要求。因此,本文方法与其他方法相比具有良好的抗差性。
3.3 某实际省网系统测试
3.3.1 实际电网估计精度测试
为了能进一步验证本文算法在实际电网中的估计性能,本文对实际电网运行数据进行试验。其基础拓扑的等效拓扑信息为1 389 个节点和2 419 条支路。本文输入的量测值包括节点电压幅值量测以及首末端支路功率量测,其量测冗余m=3.67。
为了能直观地表现出某一断面全网估计误差情况,图4 为整个省级电网某一断面的节点电压幅值和支路相角差最大绝对误差区间分布图。
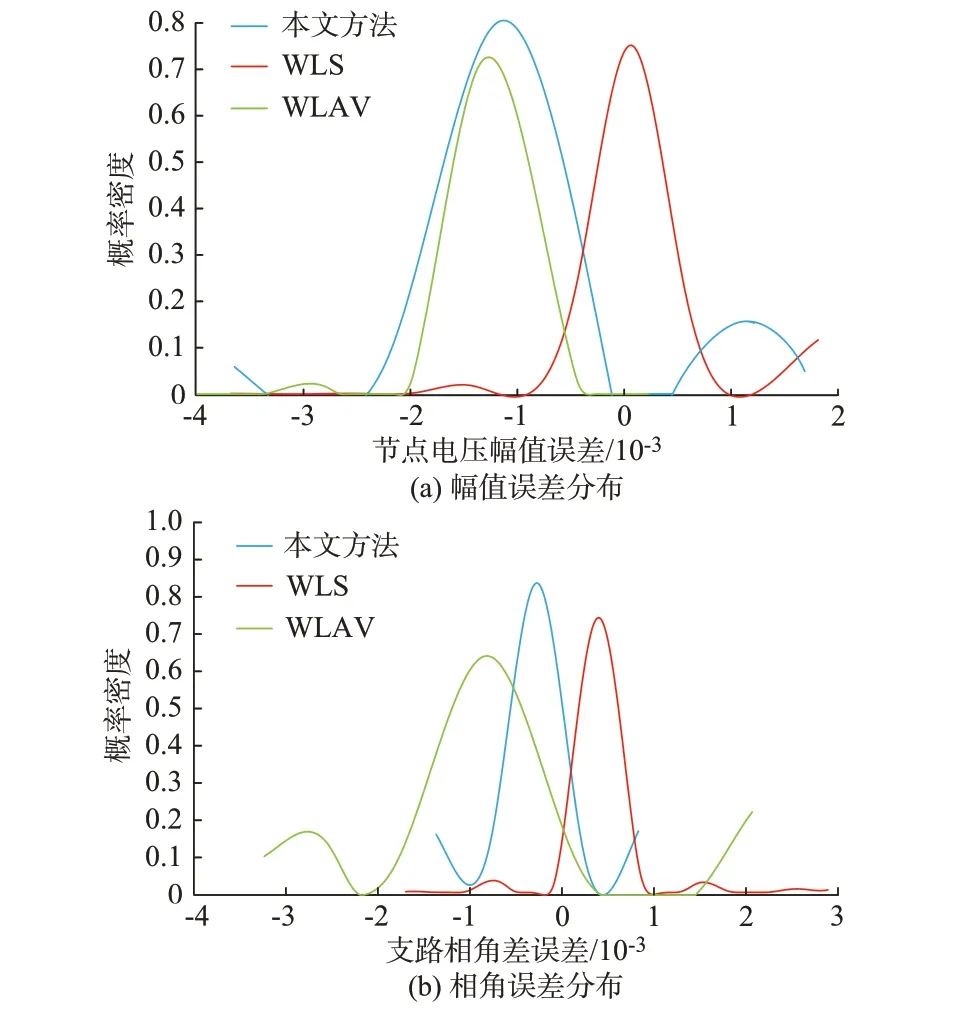
图4 实际省级电网状态估计误差分布图Fig.4 Error distribution curves of State estimation for actual provincial grid
从图4 可以看出,在仅含高斯白噪声的情况下,本文方法的估计误差主要集中在(-10-3,10-3)内,而WLS 和WLAV 误差基本在(-10-3,10-3)及该区间外。DNN 估计精度基本达不到状态估计要求,不予展示。因此,本文方法在实际电网中同样能有较传统方法更好的估计性能。
3.3.2 实际电网鲁棒性测试
本节在实际电网的量测数据中加入混合坏数据,测试本文方法在实际系统中的鲁棒性。
附录C 图C2 为该省级电网支路1 的首端功率在本文方法、WLS、WLAV 和DNN 的估计结果与潮流真值进行比较得到的最大绝对误差。
从附录C 图C2 和表4 可以看出,在添加混合坏数据情况下,本文提出的方法在绝大部分支路和节点的估计精度都比传统方法要高。节点电压幅值的最大绝对值误差较WLS 和WLAV 分别提高了62.8%和41.2%;支路相角差的最大绝对值误差较WLS 和WLAV 分别提高了68.6% 和65.6%。因此,本文方法在实际系统中具有较好的鲁棒性。

表4 实际省级电网不同方法状态估计精度对比Table 4 Comparison of state estimation accuracy of actual provincial grid in different methods
为了能直观地看出实际电网拓扑变化前后各个电气量的变化,本文采用支路1 首端功率进行结果展示。
图5 为某省级电网在加入坏数据时拓扑变化前后的首端功率变化图。从图中可以看出,在系统中存在坏数据时,其支路功率的估计精度仍在既定的要求范围内。
在量测数据中分别加入10%~70%的坏数据,状态估计精度见附录C 图C3。
3.4 估计效率对比
传统状态估计算法的基本原理是基于雅可比矩阵迭代来寻找最优解。该方法受系统规模影响较大,尤其是在大电网下,状态估计的计算效率明显下降。而数据驱动状态估计只有离线训练阶段受系统规模影响较大,在线应用阶段受系统规模影响较小。因此,本文提出的基于深度迁移学习的状态估计方法不仅能满足状态估计鲁棒性的要求,也可以满足其实时性的要求。
由表5 可以看出,随着系统规模增大,传统的模型驱动状态估计算法所用时间受系统规模影响较为明显。尤其是在大系统下运行WLAV 时,估计方法已经很难满足状态估计在线应用的实时性要求,但从不同规模的系统测试结果来看,本文算法的在线估计效率可以保持在一定范围内,基本不受系统规模影响。在某实际省级电网的算例仿真测试中,本文方法的计算效率较传统的WLS 和WLAV 分别提升了6.23%和71.05%。
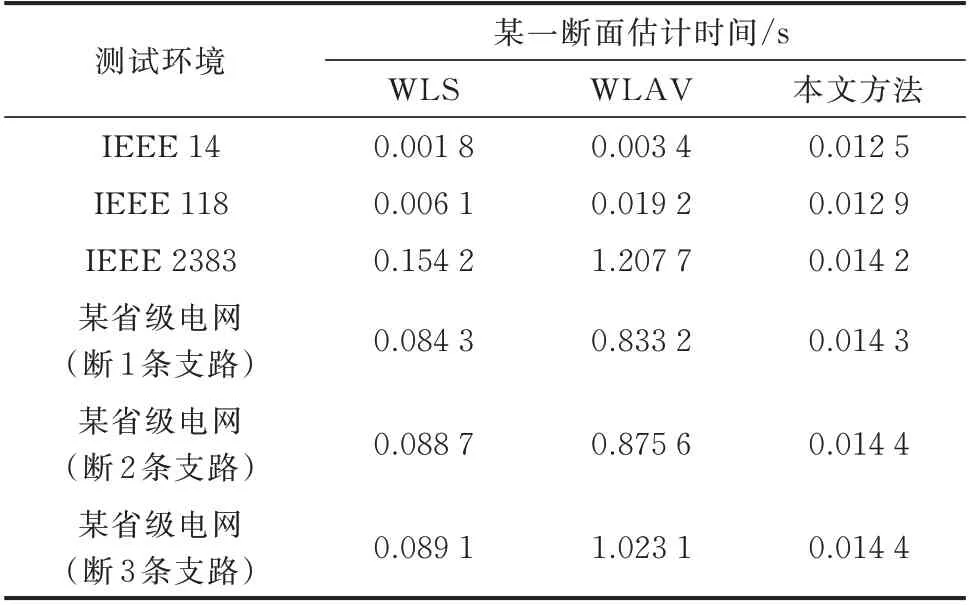
表5 各种算法的状态估计效率Table 5 Efficiency of state estimation for various algorithms
4 结语
面对拓扑时变导致数据驱动状态估计模型估计性能较差的缺陷,本文提出了基于深度迁移学习的状态估计方法,解决了因电网实际运行过程中拓扑变化导致的数据驱动估计器不可用的问题。通过IEEE 标准系统和某实际省网的算例测试,得出以下结论。
1)基于深度迁移学习进行原拓扑和新拓扑之间模型迁移,提高了数据驱动状态估计模型的泛化性能。
2)本文通过含噪声的增广网络以及数据驱动方式,可以同时满足大电网状态估计的鲁棒性和实时性要求。
3)本文方法建立在新拓扑样本有一定积累或历史数据库中含有新拓扑少量样本的情况下进行模型迁移,后续可以研究该方法在无数据积累情况下新拓扑的状态估计。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
