基于升维线性规划的主动配电网故障区段定位方法

2021-12-29李振钊王增平张玉玺

电力系统自动化 2021年24期

李振钊，王增平，张玉玺，乔鑫

（新能源电力系统国家重点实验室（华北电力大学），北京市 102206）

0 引言

配电网故障定位作为故障隔离和自愈的前提，对提高供电可靠性有着重要作用［1-2］。随着碳达峰、碳中和目标的提出，光伏、风电等分布式电源（DG）将大规模接入配电网，构成主动配电网。与传统配电网相比，主动配电网的DG 渗透率较高，拥有主动控制和管理模式（包括DG 优化调度、配电网重构、需求侧管理等），运行方式更加灵活［3］。DG 的接入和复杂多变的运行方式使配电网故障时的电流分布特征发生改变，传统配电网三段式电流保护的各段之间难以配合，选择性和可靠性不能得到保证［4-5］。

目前，国内外学者针对主动配电网保护方法进行了多方面探讨。文献［5］提出基于故障分量的纵联保护原理，消除了负荷电流的影响。文献［6］提出通过实时检测线路两端的故障暂态波形，构造时频矩阵进行故障定位。文献［7］利用斯皮尔曼等级相关系数量度两侧暂态电流波形的差异，构造了纵联保护新原理。

配电网自动化技术的快速发展使基于馈线终端单元（FTU）的故障区段定位方法成为当前的研究热点，配电网自动化与继电保护一体化是未来的必然趋势。文献［8］指出利用主站接收的多点FTU 遥信信息进行故障区段定位的数据通信量小、定位速度快。FTU 装配故障电流检测元件和方向元件之后既可以判断是否流过故障电流，也可以判断故障电流方向。文献［9］以实现主站集中式和分布式故障区段定位为目标，综合考虑高渗透率DG 并网、各种主动控制和管理模式、孤岛运行模式及多元负荷接入，提出适用于主动配电网的过流整定方法，为本文方法提供了良好的过流信息来源。

通过FTU 遥信数据进行定位主要经历如下阶段。第1 阶段：基于矩阵思想的故障区段定位［10-11］，矩阵法定位速度快、原理简单，但当FTU 上传的故障信息发生畸变时，矩阵法易发生误判或者漏判。文献［10］使用遥测信息对关键节点信息进行校正，以提高矩阵法的容错性。与矩阵法思想类似，文献［11］通过链表的形式与配电网的拓扑结构建立联系，但仅对于出现矛盾信息的部分信息畸变有容错能力。第2 阶段：利用人工智能技术进行故障区段定位，找到最能解释FTU 上报信息的故障馈线［12］，如神经网络［13］、贝叶斯网络［14］和智能优化算法［15-19］。智能优化算法具有容错性高、适用性强的优点，但存在“未成熟收敛”和数值稳定问题。第3 阶段：使用整数线性规划进行故障区段定位。文献［20-21］使用0-1 整数线性规划对传统配电网进行故障区段定位，提高了定位速度。但是针对主动配电网故障区段定位的整数线性规划方法［22-23］不能对畸变发生的所有情况具有容错性，且均是以单点故障假设为前提。

综上，虽然利用FTU 遥信信息进行故障区段定位取得了很大进展，但仍存在以下问题：①主动配电网故障区段定位的整数线性规划方法容错性能有限，当FTU 信息发生畸变时故障区段定位可靠性不高；②主动配电网故障区段定位速度有待提高；③极端天气或突发情况下，配电网可能发生多点故障［24］，利用整数线性规划的故障区段定位方法尚未解决此问题。

本文从主动配电网故障区段定位的需求出发，针对上述主动配电网故障区段定位面临的问题，提出基于升维线性规划的主动配电网故障区段定位方法。首先，建立相关拓扑信息矩阵用于描述含DG的配电网拓扑结构。然后，以最小故障集理论和状态逼近思想为基础，构建适用于整数线性规划、具有高容错性的目标函数。在此基础上，通过升维将适用于多点故障的开关函数线性化，将原问题转化为系数矩阵高度稀疏且只含0-1 变量的整数线性规划问题。最后，通过配电网故障区段定位仿真测试验证了所提算法的有效性和容错性。

1 配电网故障区段定位原理

1.1 故障电流编码方式

当配电网发生故障后，自动化开关处的FTU 会检测到电流越限并将过流信息上传至数据采集与监控（SCADA）系统。传统配电网发生故障后，故障电流由系统主电源流向故障点，仅用0、1 就可以表示故障电流的信息特征。然而，DG 的接入使得故障电流呈现双向流动的特点，传统的过流编码方式不再适用。因此，本文规定从系统主电源到各分支线路末端的方向为电流正方向，用Ii表示主动配电网的故障电流信息。

对于馈线总数为D的配电网，本文使用si(i=1，2，…，D)表示馈线是否发生故障，即

1.2 开关函数

根据配电网的功率传输机制，自动化开关在馈线状态的联系下形成了一个具有因果关系的整体。典型辐射状单电源配电网如图1 所示。图中：黑色方点为自动化开关（包括断路器和自动化装置等）；2 个黑色方点之间的区域为该自动化开关管理的馈线，馈线编号与相邻上游开关编号一致；L为负荷。假设馈线6 发生故障，自动化开关S1至S2、S5至S6处的FTU 检测到电流越限，此时称馈线6 是自动化开关S1至S2、S5至S6的因果设备。图1 中各自动化开关对应的因果设备集如表1 所示。

图1 典型辐射状单电源配电网Fig.1 Typical radial distribution network with single power source

表1 配电网中自动化开关对应的因果设备Table 1 Causal equipment corresponding to automatic switches in distribution network

采用状态逼近思想进行故障区段定位时，将配电网中故障电流信息与馈线故障状态联系起来的函数称为开关函数，开关函数以馈线状态si为自变量。以图1 所示的单电源T 形配电网为例，开关函数可以表示为自动化开关所有因果设备的“或”运算值，其表达式如式（3）所示。

式中：Ii(s)为节点期望值；sk为自动化开关因果设备k的状态，k=1，2，…，W，其中W为自动化开关的因果设备总数；∏表示逻辑“或”运算。

对于含DG 的配电网，规定节点i与主电源之间所有线路构成的集合称为节点i的上游区域，其他线路集合为节点i的下游区域，并构建适用于多点故障的开关函数［15］如式（4）和式（5）所示。

式中：Ii，u(s)和Ii，d(s)分别为以开关i为界限的上游线路开关函数和下游线路开关函数；Ku和Kd分别为上、下游电源投切系数，电源接入时取值为1，反之为0；si，Su和si，Sd分别为从节点i到上游线路所连接的电源Su和到下游线路所连接的电源Sd所经过的馈线状态值；si，u和si，d分别为节点i的上、下游馈线的状态值。

1.3 目标函数

利用整数线性规划进行故障区段定位的本质是基于状态逼近的思想，找出最能解释所有故障电流信息的馈线。在此过程中，目标函数的构建极为重要，多数学者普遍采用类似于式（7）的目标函数［23］。

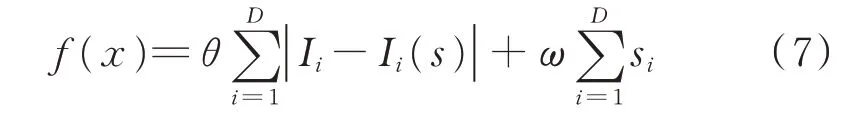
式中：θ和ω为权重系数，取值范围为[0，1]。|Ii-Ii(s)|反映了故障馈线状态值与真实值的接近情况，绝对值越小，说明此馈线故障的可能性越大。同时，式（7）等号右边的最后一项考虑了“最小故障集”理论，增加这部分有利于避免漏判、误判现象的发生。在不发生故障、没有畸变的情况下，f(x)的值为0。

然而，FTU 不同类型的信息畸变对式（7）中目标函数的影响不同。例如：当主站接收的FTU 信息为1 而实际故障信息为-1 或主站接收的FTU 信息为-1 而实际故障信息为1 时，目标函数值增加2；对于其他种类的FTU 信息畸变，目标函数值增加1。因此，为保证各种信息形式的畸变对目标函数的影响一致，本文提出基于“广义异或”形式的新型目标函数。式中：∨表示逻辑“或”；∧表示逻辑“与”；⊕表示逻辑“异或”；λ和μ为权重系数，取值范围为［0，1］；Ii，u1和Ii，d1分别为FTU 上传真实值所对应的上、下游线路开关函数的第1 种取值可能；Ii，u2和Ii，d2分别为FTU 上传真实值所对应的上、下游线路开关函数的第2 种取值可能，对应情况如表2 所示。

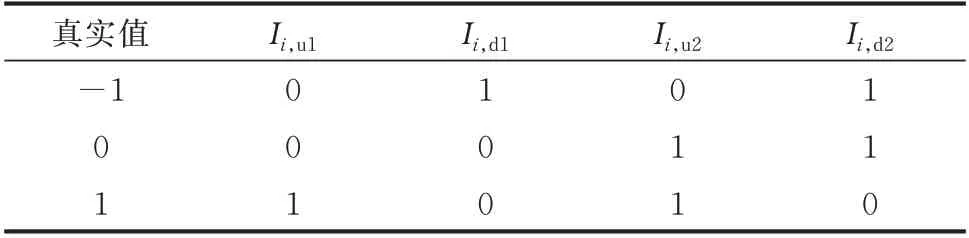
表2 FTU 真实值和Ii，u、Ii，d的关系Table 2 Relationship between real value of FTU and Ii，u or Ii，d

Ii，u1⊕Ii，u(s)是比较FTU 真实值推测的第1 种可能的开关函数和上游线路开关函数，相同时取值为0，不同为1；Ii，d1⊕Ii，d(s)是比较FTU 真实值推测的第1 种可能的开关函数与下游线路开关函数，如果Ii，u1、Ii，u(s)和Ii，d1、Ii，d(s)都相同，说明FTU 真实值属于第1 种情况，即(Ii，u1⊕Ii，u(s))∨(Ii，d1⊕Ii，d(s))取值为0。如果Ii，u1、Ii，u(s)和Ii，d1、Ii，d(s)有任何一个不相同，说明FTU 真实值与第1 种可能不同，此时(Ii，u1⊕Ii，u(s))和(Ii，d1⊕Ii，d(s))中不相同的部分为1，(Ii，u1⊕Ii，u(s))∨(Ii，d1⊕Ii，d(s)) 取值为1，所以使用“或”运算连接这两部分。只要FTU 真实值推测的任何一种可能的开关函数取值与Ii，u(s)、Ii，d(s)相同即可，因此使用“与”运算将这2 种可能连接，式（8）的具体说明见附录A。

2 主动配电网故障区段定位方法

本章通过升维的方式将配电网故障区段定位问题转换为0-1 整数线性规划问题，具体形式如式（9）所示。

式中：A为约束条件的系数矩阵；b为资源向量；s为由si组成的向量；ci为价值系数；n为馈线数量。

2.1 拓扑信息矩阵的建立

为了便于表示开关函数，首先建立拓扑信息矩阵，以图2 所示的双电源T 形配电网为例，说明拓扑信息矩阵的建立过程。

图2 双电源T 形配电网Fig.2 T-type distribution network with dual power sources

步骤1：建立各节点与系统主电源及所有DG 的连接关系矩阵。由于图2 只含有一个系统主电源和一个DG，因此只需建立2 个电源连接关系矩阵，分别记为E1和E2，E1表示各节点与系统主电源的连接关系，E2表示各节点与DG 的连接关系。以E1为例说明矩阵的建立过程，矩阵中的元素E1(i，j)表示第i个节点到主电源所经过的馈线是否包含馈线j，如果包含馈线j，则E1(i，j)取1；反之，取0。

步骤2：建立各节点的下游矩阵Pd和上游矩阵Pu，矩阵为方阵，维数取决于配电网节点的总数。以下游矩阵Pd为例，矩阵中的元素Pd(i，j)表示节点i的下游是否有馈线j，如果有馈线j，则Pd(i，j)取值为1；反之，取0。

步骤3：建立各节点与系统主电源及所有DG 的上游、下游矩阵Hu和Hd。将系统主电源视为电源1，DG 视为电源2。以上游矩阵Hu为例，矩阵中的元素Hu(i，j)表示电源j是否可以使节点i产生正方向的过电流，如果是则Hu(i，j)取值为1；反之，取0。

步骤4：计及DG 投切，当DG 接入配电网时，Hu和Hd按步骤3 建立；当DG 未投入时，Hu和Hd中该DG 对应列的所有元素置0。文献［22］介绍了联络开关开合状态对故障区段定位方法的影响，当只有联络开关断开、原有配电网形成2 个分裂的配电子网时，可以分别针对2 个子网建立故障区段定位模型。当一个联络开关断开、另一个联络开关闭合，但配电网依然保持辐射状时，故障区段定位方法可以通过改变系数矩阵中的相关元素以适应拓扑结构的变化。本文所提故障区段定位对拓扑结构变化时的应对方案与文献［22］相似，通过改变系数矩阵的部分元素来适应拓扑结构的变化。

2.2 逻辑关系运算线性化

使用智能优化算法进行故障区段定位的原因是故障区段定位问题的目标函数和开关函数是非线性的，本节通过升维将低维空间中采用智能优化算法求解的非线性规划问题转变为高维空间中可以利用整数线性规划求解的问题。根据上文建立的6 个拓扑信息矩阵，构建整数线性规划的系数矩阵A。

1）根据矩阵E1计算各节点到系统主电源路径上所有馈线状态的逻辑运算值，分别利用虚拟开关变量s7至s12表示节点1 至6 的逻辑“或”运算结果，具体形式如式（13）所示。

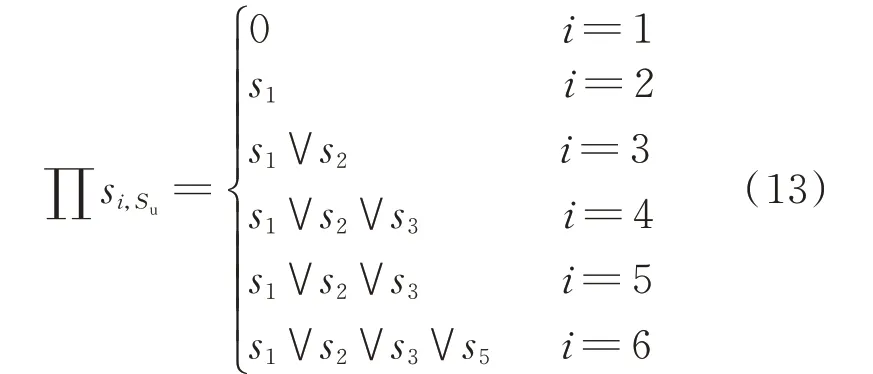
借助逻辑“或”运算的线性化思想，对式（13）中的各表达式进行线性化处理。以节点6 为例，借助虚拟开关变量s12进行转化，具体转化结果如式（14）所示。

为了表示方便，将式（14）表示成系数矩阵的形式，如式（15）所示。

依照上述变换原则，分别利用虚拟开关变量s7至s12对式（14）中节点1 至6 的逻辑运算结果进行替换。然后，依次对其进行线性化处理，得到对应的不等式约束条件组。最后，形成6 个节点各自对应的7×6 系数矩阵A′i(i=1，2，…，6)，并将其重新组合成42×12 的系数矩阵A′。

式中：E′1和E″1均为42×6 的矩阵。

同理，引入虚拟开关变量s13至s18，并根据步骤1至4 对基于矩阵E1形成的所有逻辑运算表达式进行线性化处理，最终得到2 个42×6 的系数矩阵E′2和E″2。引入虚拟开关变量s19至s24，对基于下游矩阵Pd而形成的所有逻辑运算表达式进行线性化处理，最终得到2 个42×6 的系数矩阵P′d和P″d。引入虚拟开关变量s25至s30，对基于上游矩阵Pu而形成的所有逻辑运算表达式进行线性化处理，最终得到2 个42×6 的系数矩阵P′u和P″u，将上述矩阵进行合并，得到矩阵B，如式（17）所示。

2）引入虚拟开关变量s31至s42，使其分别等于s7至s18的逻辑“非”，即s31至s42是s7至s18的互补运算结果。

以s31=1-s7为例，其对应的不等式关系如式（19）所示。

3）引入虚拟开关变量s43至s48，结合上游电源矩阵Hu，对由各节点所有上游电源作用下形成的式（18）进行逻辑“或”运算。引入虚拟开关变量s49至s54，结合下游电源矩阵Hd，对由各节点所有下游电源作用下形成的公式进行逻辑“或”运算。

以式（20）中第6 个节点为例，说明变量s48的等价约束条件。

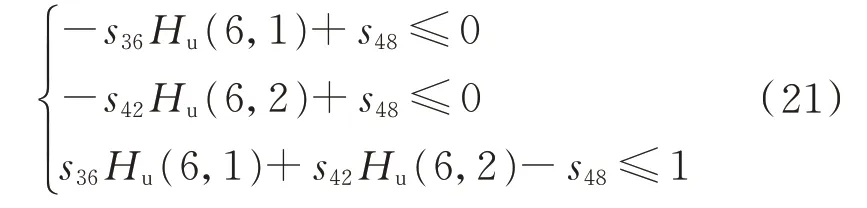
4）引入虚拟开关变量s55至s60分别作为6 个节点的上游线路开关函数Ii，u(s)，对节点i所有上游电源的逻辑“或”运算结果和下游馈线的逻辑“或”运算结果进行逻辑“与”运算。引入虚拟开关变量s61至s66作为6 个节点的下游线路开关函数Ii，d(s)的值，对节点i所有下游电源的逻辑“或”运算结果和上游馈线的逻辑“或”运算结果进行逻辑“与”运算。

以s55=s19∧s43为例，其对应的不等式关系如式（23）所示。

5）根据表2 并结合SCADA 系统实际接收到的过流信息推测出Ii，u1、Ii，d1、Ii，u2、Ii，d2，根据式（8）比较真实值推测的上游线路开关函数和下游线路开关函数与状态值计算的开关函数是否相同。使用虚拟开关变量s67至s78表征Ii，u1和Ii，u(s)的异同，其中，s67至s72是辅助变量。以s73为例，说明逻辑“异或”的线性化表示形式。

利用虚拟开关变量s79至s90比较Ii，d1与Ii，d(s)是否相同，逻辑“异或”的结果为s85至s90。引入虚拟开关变量s91至s102比较Ii，u2与Ii，u(s)是否相同，s103至s114表示Ii，d2和Ii，d(s)的异同。使用s115至s120分别对s73至s78和s85至s90进行逻辑“或”运算，利用s121至s126分别对s97至s102和s109至s114进行逻辑“或”运算。最终，开关函数的上游线路开关函数和下游线路开关函数表达形式为：

6）引入s127至s132分别表示s115至s126和s127至s132的逻辑“与”运算结果，即6 个节点的FTU 上传电流信息与状态值的“广义异或”运算结果。

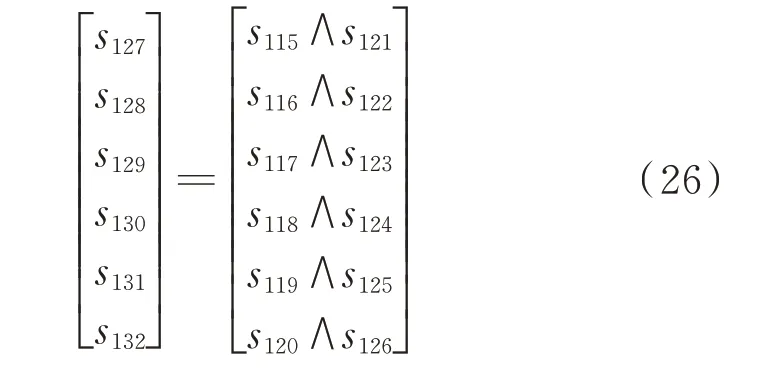
综上，基于整数线性规划的主动配电网故障区段定位方法的数学表达形式如式（27）所示。

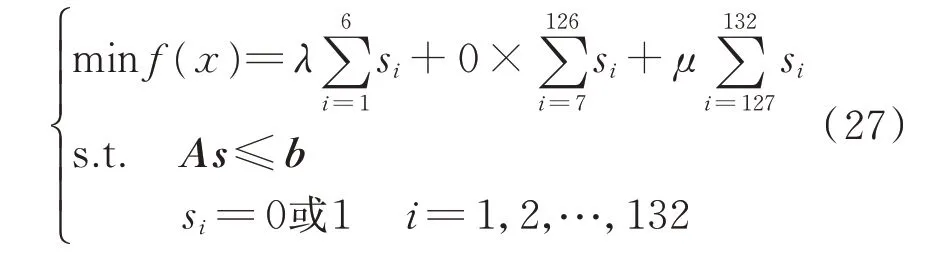
3 求解策略与求解步骤

对于节点数为m、系统主电源和DG 总数为l的配电网，形成矩阵A的行数（约束条件个数）为m2l+2m2+5ml+39m，列数（变量个数）为2ml+18m，证明过程见附录B，且矩阵A高度稀疏。求解整数线性规划的方法有很多，如：分支定界法、割平面法、隐枚举法、匈牙利法等。本文算例使用MATLAB 调用Cplex 工具箱求解，主动配电网故障区段定位的流程图见附录B 图B1，具体步骤如下。

1）对主动配电网中的馈线、自动化开关、DG 进行编号，规定网络的唯一正方向。

2）根据主动配电网的拓扑结构，建立拓扑信息矩阵。

3）通过升维形成系数矩阵A、资源向量b和目标函数。

4）使用MATLAB 求解整数线性规划问题。

5）输出故障馈线对应的编号。

4 算例仿真

使用MATLAB 2018a 以图3 所示的含3 个DG的IEEE 33 节点系统为例进行仿真测试。图3 中，最左侧电源为系统主电源。经过多次调试，式（8）中的权重系数λ和μ分别取1.0 和0.5。为验证本文所提方法在不同情况的适应能力，本章首先以IEEE 33 节点系统为基础从多个角度进行故障区段定位仿真。为进一步验证所提方法在更大规模配电网的适用性，对以IEEE 69 节点系统为基础的配电网进行故障区段定位仿真测试。

图3 IEEE 33 节点馈线配电系统Fig.3 IEEE 33-bus feeder distribution system

4.1 有效性测试

在考虑DG 的动态投切的情况下，分别设置单点故障、两点故障、三点故障（FTU 上传信息无畸变）来验证本文所提算法的有效性和准确性。表3中［K1，K2，K3］分别为DG1、DG2、DG3 的投切系数，DG 接入配电网，则其对应的值为1；反之，取0。

表3 的结果说明在FTU 上传信息不发生畸变的情况下，故障区段定位算法可以适应DG 的动态投切。该算法可以准确定位出多点故障，且目标函数值是故障馈线数量的50%。当所有DG 退出运行时，该方法也能准确定位故障馈线，说明该算法可以适用于含DG 和不含DG 的配电网。

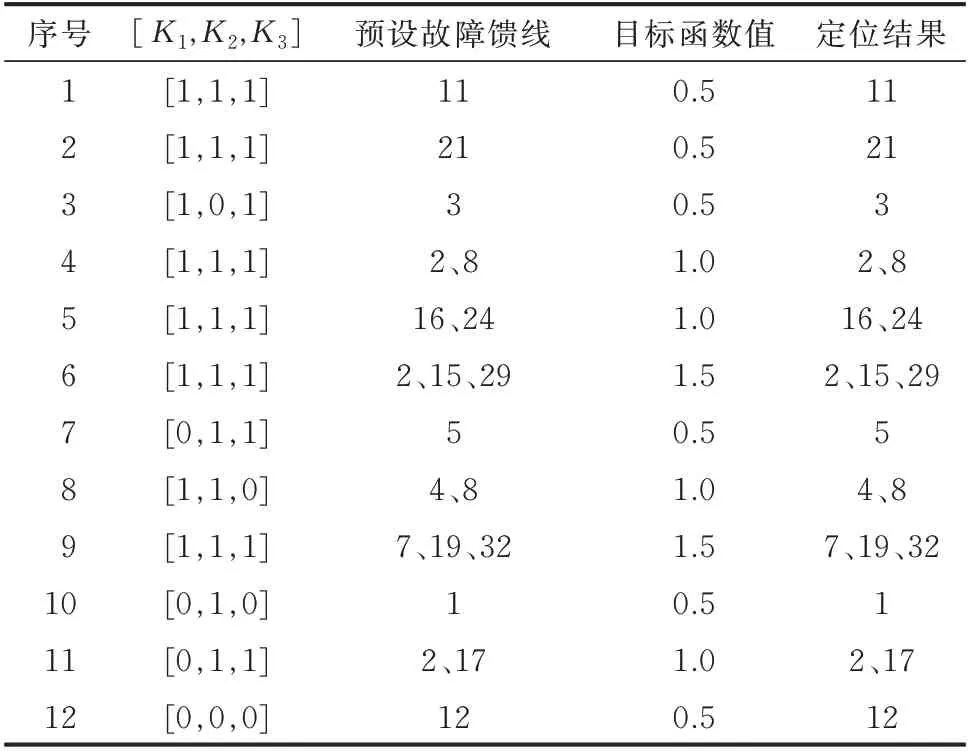
表3 算法有效性测试Table 3 Validity test of proposed algorithm

4.2 容错性分析

FTU 电流信息畸变分为漏报、误报2 种情况，漏报是指电流信息越限而FTU 未上报至SCADA系统。误报是指SCADA 系统接收到了越限信息，但实际情况与之不符。FTU 信息畸变的情况见附录C 图C1。

为验证在FTU 上传信息畸变的情况下该方法的准确性，本文在Intel Core i7-7500U CPU 2.70 GHz 平台上的MATALB 环境中采用整数线性规划的方法对单点故障、两点故障、三点故障情况下不同数量和位置的信息畸变情况进行仿真计算，定位结果以及求解时间如表4 所示。

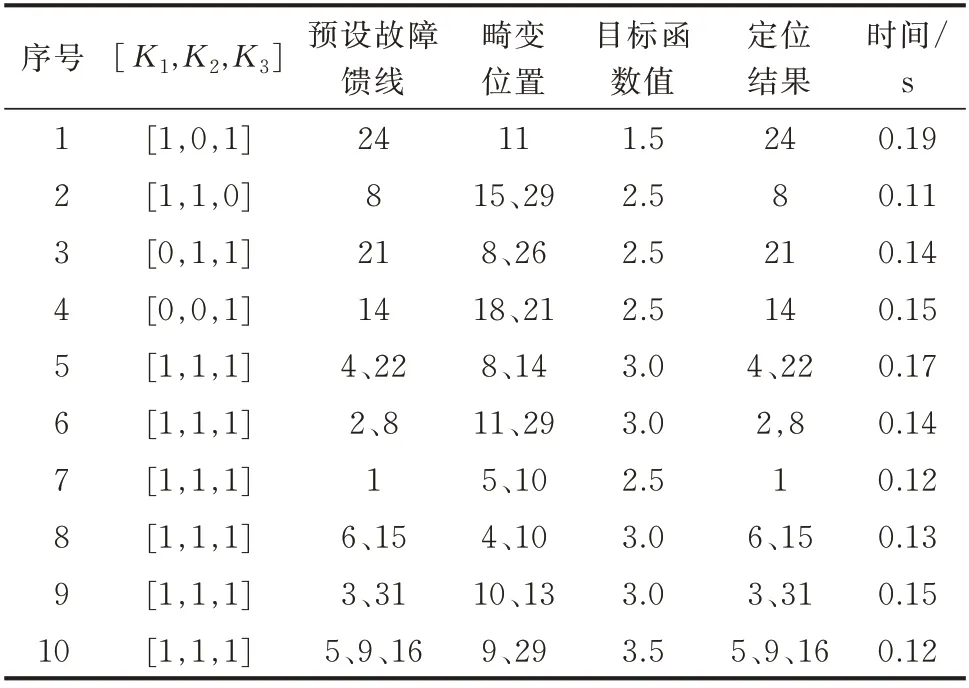
表4 算法容错性测试Table 4 Fault tolerance test of proposed algorithm

从表4 的仿真计算结果可以看出，本文提出的故障区段定位方法对IEEE 33 节点配电网进行故障区段定位时，在畸变数量为0～2 个的情况下均可以实现准确定位，且定位时间在0.2 s 以内，可以满足继电保护定位的速动性要求。

4.3 性能比较

为表明本文所提方法的性能优势，以图3 所示的配电网为例，分别使用本文方法、文献［18］提出的蝙蝠算法（BA）以及文献［15］提出的基于二进制粒子群优化（BPSO）和遗传算法（GA）的混合算法（简称BPSOGA）进行故障区段定位效果对比，以式（7）作为目标函数，θ和ω分别取1.0 和0.5。本文沿用文献［18］和文献［15］的初始化参数设置：二进制粒子种群规模N1=50；学习因子为1.5；遗传种群规模N2=50；交叉概率为0.7；变异概率为0.2/30；最大迭代次数限制为100；蝙蝠种群的初始脉冲响度A=0.6；初始脉冲率R=0.5；脉冲频率范围为[0，2]；最大迭代次数为100。本文所提方法与BA、BPSOGA的对比见附录C 表C1。智能优化算法在进行故障区段定位时一般采用设置最大迭代次数的方法停止迭代，容易产生“未成熟收敛”现象，导致故障区段定位的误判或漏判。

智能优化算法初始化的过程是随机的，同样条件下故障区段定位的结果可能不同。因此在表5 所示的故障及畸变的情况下，使用本文方法、BA 和BPSOGA 重复仿真运行50 次，并统计故障区段定位的正确率，如图4 所示。

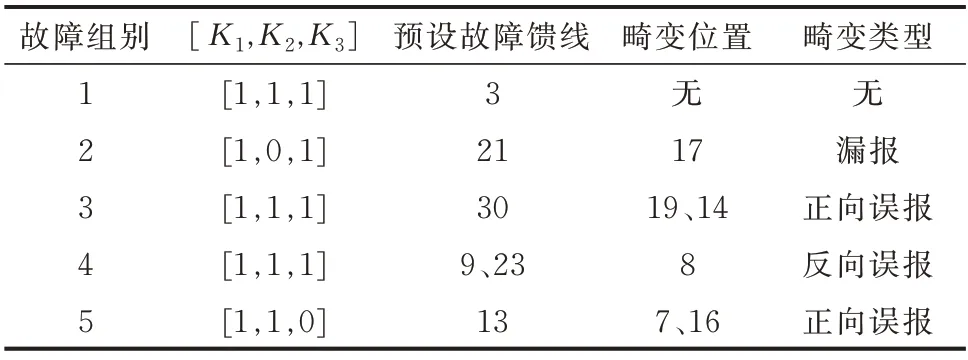
表5 故障情形的设定Table 5 Setting of fault situation

图4 不同故障情形下各方法的定位准确率对比Fig.4 Comparison of location accuracy with eachmethod in different fault situations

由图4 可以发现，在故障位置相同、畸变相同的情况下，本文提出的基于升维线性规划的故障区段定位方法准确率高于其他算法，且50 次仿真结果都能准确定位出故障。智能优化算法实现简单、具有一定容错能力的优点，但算法的稳定性不好，容易发生“未成熟收敛”的现象，从而导致故障误判或漏判。BPSOGA 通过双种群进化和信息交换的策略降低了“未成熟收敛”的概率，但不能完全根除此现象。此外，智能优化算法的收敛速度较慢，以表5 中的第2 组故障情形为例，附录C 图C2 为本文所提方法与BA、BPSOGA 的时间对比结果，优化算法的平均求解时间超过2 s，本文方法求解速度优于优化算法。

文献［20-23］利用整数线性规划方法进行故障区段定位，文献［20-21］以不含DG 的传统配电网为研究对象，因此本文与文献［22］及文献［23］进行对比。文献［22］和文献［23］均是通过增加2 个辅助变量Ui(s)和Vi(s)将故障区段定位问题转变为线性规划问题。然而，即使在单点故障假设的前提下，这种方法的容错性也是有限的。畸变类型有附录C 图C1 所示的6 种情况，即、、、、、，文献［22］和文献［23］均不能对（从1 畸变为-1）和（从-1 畸变为1）的情况进行故障区段定位。以文献［22］为例，选取式（7）为目标函数，且θ=1，ω=0，则目标函数和约束条件为：

根据式（29）画出可行域如图5（a）所示，Ui(s)和Vi(s)取整数。同理，当畸变类型为时，可行域如图5（b）所示。由图可见，当畸变类型为和时，约束条件互相矛盾，不能求解出故障区段。通过附录A 表A1 及附录C 表C1 可知，本文所提方法可以对所有畸变类型进行故障区段定位。

图5 不同畸变情形下的可行域示意图Fig.5 Schematic diagram of feasible region in different distortion situations

4.4 DG 以“T”接方式接入时算法的适用性分析

根据DG 接入配电网的运行规程，DG 不仅可以通过母线并网，还可以“T”接方式接入馈线。在图3的基础上，DG 以“T”接方式分别接入馈线12 和馈线30，拓扑结构见附录C 图C3。为验证本文所提算法在DG 以“T”接方式接入时的有效性，对附录C 图C3 所示配电网进行故障区段定位仿真测试。

通过表6 仿真结果可以看出，所提方法不受“T”接的影响。此外，在DG 以“T”接方式接入配电网时，配电网DG 的渗透率提高，说明本文所提方法在高DG 渗透率的情况下仍然适用。

表6 DG 以“T”接方式接入配电网时故障区段定位结果Table 6 Fault section location results when DG is connected to distribution network through“T”connection

4.5 IEEE 69 节点主动配电网的适应性分析

为验证本文所提方法在更大规模主动配电网的适用性和实时性，以附录C 图C4 所示的IEEE 69 节点配电网为例进行故障区段定位仿真测试，每种情况分别仿真50 次，故障区段定位的平均时间和准确定位的次数如表7 所示。

由表7 可知，在IEEE 69 节点配电网中，本文所提方法准确可靠，求解时间均在1 s 以内。当主动配电网节点过多时，可以使用文献［25］提出的分层故障区段定位策略先对配电网进行分层以提高故障区段定位的效率。同时，文献［26］指出将全部故障信息上传至主站层会使运算量加大。因此，可在配电网环网柜、开闭所、配电所或箱变等出线的智能开关处增加站域层以减少故障处理时间。