考虑发电机阀点效应的改进拉格朗日松弛有功调度策略

陈建华，丁 冬，于希娟，丁 红，忻 煜

（1. 国网冀北电力有限公司，北京市 100053；2. 国网北京市电力公司，北京市 100031；3. 国网北京市电力公司电力科学研究院，北京市 100075）

0 引言

经济调度问题是电力系统运行中最重要的优化问题之一［1-2］，其目的是在保证电力系统安全运行的前提下，通过优化调整机组出力实现系统运行经济性最优的目的［3-4］。目前，经济调度运行中，一般认为机组运行成本与机组出力之间为简单的二次多项式关系。但实际上，对大型发电机组来说，其进气阀突然开启时出现的拔丝现象会在机组耗量曲线上叠加一个脉动效果，产生阀点效应，从而导致经济调度问题呈现非光滑和非凸特性，增加了模型的复杂度，给优化求解带来较大难度［5］。

以往对于考虑阀点效应的有功调度问题的研究主要以启发式算法为主，包括粒子群优化算法［6-7］、自组织迁移算法、人工蜂群算法、人工免疫算法、共生生物搜索算法、和声搜索算法［8-14］等。部分研究将2 种或多种算法进行混合求解［15-19］，其中先由一种方法进行初步搜索，以缩小搜索范围，然后用另外一种方法进行精细搜索，以达到最优。启发式算法的优点在于对优化问题的形状要求较少，对于非凸非光滑优化问题也能获得优化解。但启发式算法每一次优化结果均不相同，存在前后两次结果差别较大的情况，且结果不能复现，因此，目前尚难以在实际现场应用。

在数学优化领域，对于此类非凸非光滑优化问题，一般采用分段线性化方法进行求解，但由此会产生2 个问题：一是优化模型中引入了整数变量，从而变为混合整数规划问题，降低了求解效率；二是对于存在多个局部最优点的优化问题，可能会出现最优解来回跳变，从而导致优化过程不收敛问题。

本文提出一种改进的拉格朗日松弛有功调度算法，以考虑发电机阀点效应影响。提出一种二次多项式分段拟合算法及基于近端梯度法的增广求解策略，能够在确保结果最优性的基础上加快收敛速度。

1 考虑阀点效应的有功经济调度问题模型

有功经济调度问题模型的目标函数和约束条件分析如下。

1）目标函数

一般以火电机组煤耗最小作为有功经济调度问题的优化目标函数，如式（1）所示。

式中：f(pi)为火电机组i的煤耗成本，pi为机组i的有功出力；ai，bi，ci为机组i的煤耗成本系数。

当考虑阀点效应时，式（1）将转变为式（2）。

式中：n为系统中所有火电机组数量；ei和fi为常数；为第i台机组的有功出力下限。

2）约束条件

发电负荷平衡约束为：

式中：D为系统负荷需求预测值。

发电机出力限值约束为：

输电断面容量约束为：

可以看出，当考虑常规机组阀点效应时，优化目标将由传统的凸优化问题转变为非凸非光滑优化问题。由于目前未有针对这一问题的有效求解策略，使得经济调度问题优化求解困难。

2 改进拉格朗日松弛法求解算法

2.1 整体求解流程

对第1 章中的有功经济调度模型，采用拉格朗日松弛法进行求解，对应的拉格朗日对偶问题如式（6）所示。

式中：C为常数项。

可以看出，式（7）可以看成是多个单机约束的优化子问题之和。因此，原优化问题可以表示为多个并行的单机优化子问题，每个子问题中的变量及约束仅与一台机组相关，而与其他机组无关。子问题的表达式如式（8）所示。

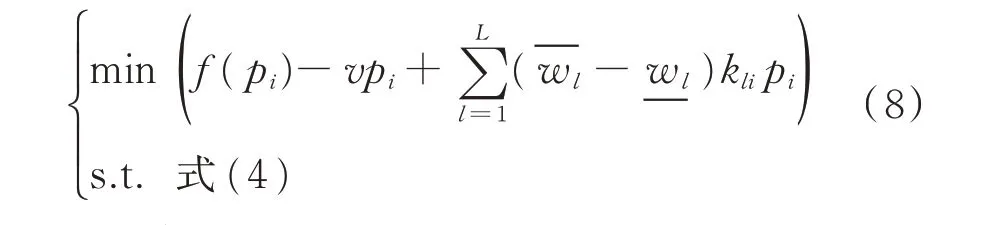
对于传统有功调度问题而言，f(pi)为二次多项式函数，因此，子问题为二次规划问题，最优解可以较容易获得。

在子问题获得最优解后，通过次梯度法更新主问题的拉格朗日乘子，并不断对主问题、子问题进行迭代，即可逐渐逼近最优解。

2.2 考虑阀点效应的改进拉格朗日松弛算法

当考虑阀点效应时，f(pi)转变为式（2）的非凸非光滑函数形式，如图1 所示，导致传统的数值优化算法不再适用。

图1 考虑阀点效应的机组煤耗成本与有功出力关系Fig.1 Relationship between coal consumption cost and active power output of generator considering valve-point effect

式中：αi，k、βi，k、γi，k为第i台机组第k分段二次拟合多项式系数。

以图1 所示的发电机有功出力曲线为例，二次多项式拟合的误差曲线如图2 所示。其中，拟合误差=|拟合值- 真实值|/机组额定出力下的煤耗成本。

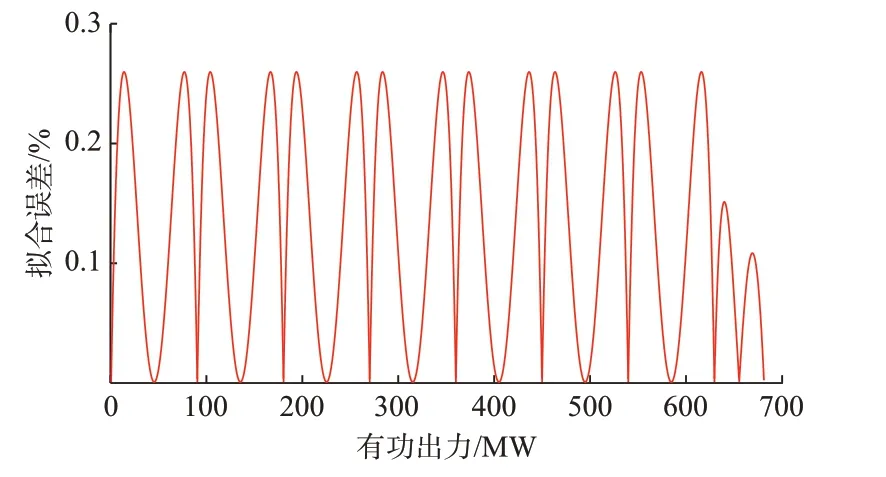
图2 拟合误差曲线Fig.2 Fitting error curve

由图2 可知，二次拟合最大误差为0.25%左右，能够满足实际应用需要。

将拟合后的二次多项式（9）代入式（2）可以得到火电机组煤耗成本为：

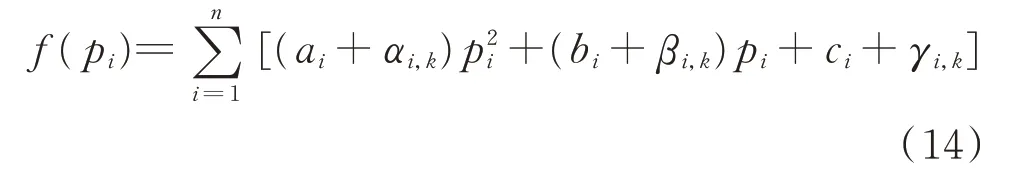
将式（14）代入式（8），可以得到此时拉格朗日子问题的表达式为：

式（15）为分段函数形式，其中，对第k分段来说，其优化目标函数为二次函数，开口方向取决于二次项系数大小，对应的二次项系数为：

因此，当ai＞4ei f2i/π2时，最优输出功率为：

当ai＜4ei f2i/π2时，最优输出功率为：

实际上，对绝大多数火电机组来说，ai取值一般在10-4～10-3之间，而ei的取值一般为102量级、fi的取值一般为10-2量级，因此，ai＜4ei f2i/π2总是成立，优化过程中一般只需要考虑式（18）一种情况即可。式（18）表明，对于开口向下的二次函数，其最小值将在某一边界处取得。因此，优化问题简化为只考虑每台机组少数几个阀点即可，此时需要松弛发电负荷平衡约束（v≥0），确保问题能够收敛。

2.3 基于近端梯度法的改进子问题求解策略

拉格朗日松弛法对原问题进行对偶求解做法的一个主要缺点是要求原问题具有凸结构，否则对偶问题的最优解与原问题之间不仅存在对偶间隙，而且导致对偶问题收敛性较差，容易出现振荡不收敛情况。

针对子问题的非连续可微特性，本文提出一种基于近端梯度法的改进子问题求解方法。近端梯度法是一种特殊的梯度下降算法，主要用于求解目标函数不可微的最优化问题。如果目标函数在某些点是不可微的，那么该点的梯度无法求解，传统的梯度下降法也就无法使用。

近端梯度法的核心思想是通过proximal 映射，将不可微函数转化为易求解的proximal 映射函数，从而实现近似求解。假设约束函数f（x）的定义域为U，则自变量x的proximal 映射为：

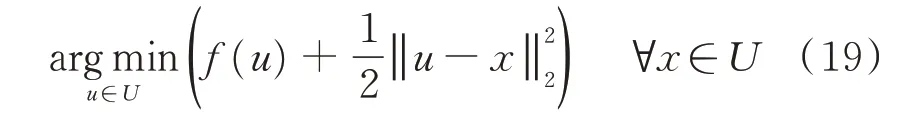
本文在上式基础上，通过在目标函数中引入惩罚因子ς，在不影响原优化问题的优化结果的基础上，加快问题收敛速度。

式中：ς为惩罚项系数；y为辅助变量。为加快收敛速度，在第λ次迭代时，本文令y取为第λ-1 次迭代时对应的有功出力。

可以看出，式（20）优化问题的最优解p*i与式（15）优化问题最优解相同，且在最优解处，有y=p*i。因此，二次惩罚项的加入不影响原优化问题的优化结果。

对于式（20）的优化问题，其目标函数的Hessian矩阵为：

当ς取值过小时，将导致优化问题Hesssian 矩阵条件数过大，从而导致优化问题病态；而当ς取值过大时，优化问题凸性不足，将导致优化问题难以收敛。因此，合适的惩罚项系数选取对于保证优化问题的最优性及高效性具有重要意义。一般来说，为保证问题的收敛性，一般要求Hessian 矩阵为正定矩阵，即：

由式（22）、式（23）可知，ς的取值区间建议为：

以2.2 节中发电负荷平衡约束松弛后获得的解作为优化初值，用式（20）替换式（15），通过对每一分段分别求解并比较各分段区间优化解的经济性即可得到最优煤耗及对应的发电机组出力。

3 算例分析

3.1 40 机测试系统仿真结果

选取文献［20］中的40 机测试系统作为研究对象，系统负荷需求为10 500 MW，惩罚项系数ς取0.01。

不考虑阀点效应时，有功调度问题转化为传统的二次规划问题，可以采用传统的拉格朗日松弛法快速求解，得到最小运行成本为118 660.2 美元。

考虑阀点效应时，采用本文方法及与其他方法优化结果比较如表1 所示。

表1 几种方法优化结果比较（40 机测试系统）Table 1 Comparison of optimization results of several methods（40-machine test system）

由表1 可见，当考虑阀点效应时，系统运行成本由118 660.2 美元至少增加到121 412.5 美元，升高了2.32%，可见发电机阀点效应特性对系统调度运行的经济性具有明显影响。

同时，本文方法计算结果为121 459.6 美元，仅比全局最优解（121 412.5 美元）高0.03%左右，但计算时间仅为1.34 s，计算效率明显高于混合整数规划法。同时，本文方法计算结果也明显优于其他6 种计算方法，且计算所需时间最短、效率最高。本文方法的收敛特性曲线如图3 所示，经过200 次左右迭代，本文方法能够快速逼近最优点。

图3 所提算法收敛特性Fig.3 Convergence characteristic of proposed algorithm

3.2 48 机测试系统仿真结果

以文献［24］中的48 机测试系统为研究对象，系统包括26 台传统火力发电机组、12 台热电联产机组及10 台供热机组。系统负荷需求为4 700 MW，供热需求为2 500 MWth，惩罚项系数ς取值为0.9。

采用本文方法与其他方法的优化结果比较如表2 所示，每一台机组的优化结果比较如附录A 表A1所示。

表2 几种方法优化结果比较（48 机测试系统）Table 2 Comparison of optimization results of several methods（48-machine test system）

由表2 可见，受优化模型目标函数、约束条件均存在强非凸性的影响，传统拉格朗日松弛法无法收敛，采用混合整数规划法可以得到最优的优化结果，但算法运行时间较长，为84.82 s，效率较低。本文方法煤耗成本仅为115 806.55 美元，仅高于全局最优解0.12%。与其他几种方法相比，本文方法煤耗成本也最低。同时，本文方法运行时间仅为6.29 s，远小于其他几种方法，计算效率高。同时，对于现场实际应用来说，本文方法具有可重复性，且只需要运行一次即可获得最优解，而启发式算法需要反复运行多次，且一般不能复现结果。

本文方法的收敛特性曲线如附录B 图B1和图B2所示。可见，经过600 次左右迭代，本文方法能够逐渐逼近最优点。根据式（23）可知，要保证结果的收敛性，惩罚项系数ς的取值范围应为[0，1.749]。对不同ς取值下的优化结果进行分析，如表3 所示。

表3 不同惩罚项系数时的优化结果比较Table 3 Comparison of optimization results with different penalty term coefficients

由表3 可见，当ς在允许区间范围内取值时，优化结果及计算效率差别不大；当ς取值超出允许区间时，优化过程不收敛。特别的，当ς取为∞时，优化模型转变为传统的拉格朗日松弛算法，此时，优化过程不收敛。

进一步，考虑不同负荷需求水平及供热需求水平，本文方法的收敛性如附录B 图B3 所示。由图B3 可见，在不同负荷需求及供热需求水平下，本文方法均能够快速收敛，证明了本文方法的鲁棒性。同时可以看出，负荷水平变化时的收敛曲线具有一定的振荡性，与不同供热需求水平下的收敛曲线具有较大差异，这是由于考虑常规机组阀点效应时优化目标函数的非凸非光滑特性导致的。

4 结语

考虑阀点效应的有功调度问题，以往的研究主要集中于启发式算法。本文提出一种基于数学规划方法的求解策略，通过对拉格朗日松弛法进行改进，并结合近端梯度算法，消除了发电机阀点效应导致的非凸非光滑特性的影响。同时，提出一种二次多项式分段拟合及基于近端梯度法的增广优化求解策略。40 机及48 机两个测试系统上的优化结果表明：本文方法收敛性好、运行效率较高，较为适合在现场实际应用。

同时，需要指出的是，考虑阀点效应的有功调度问题为非凸优化问题，由于对偶间隙的存在，拉格朗日松弛法在求解此类问题时，只能得到局部最优解。下一步需要对此进行改进，结合其他数学规划算法的优点，寻求能够快速获得全局最优解的高效算法。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。