基于改进蚁群算法的物料配送方法
2021-12-29涂海宁
涂海宁,刘 佩,黄 剑
(1.南昌大学机电工程学院,南昌 330031; 2.温州静音汽车轴承有限公司,浙江 温州 325000)
0 引言
制造业的整个生产过程都是围绕着物料进行的,物料的准时准点配送是车间正常作业的前提。Yi C F提出的准时化生产系统指出,提高物料运输效率、降低库存可以有效地降低物流成本、加快生产节奏[1]。因此,在竞争日益激烈的市场环境下,企业要想以更低的成本快速响应市场和客户的生产需求,对物料配送这一环节进行优化研究尤为必要。
物料配送优化的核心是配送路径的规划,属于带容量限制的车辆寻迹问题,该问题的研究目的可以描述为在满足约束条件的情况下,找到一条最优路径,从而实现如配送路程短、配送速度快和配送成本低等目标。目前用来解决路径优化问题的有以人工势场法[2]和A~*算法[3]为代表的经典算法,以及时下比较流行的遗传算法[4]、蚁群算法[5]、神经网络算法[6]、粒子群算法[7]和模拟退火算法[8]等智能算法。其中蚁群算法非常适合解决路径优化问题,因其具有并行性、收敛速度快等特点,并且与其他启发式算法结合程度高,但是在求解过程中,迭代一定次数后,算法容易陷入停滞状态,同时求解过程中参数的确定也多凭经验而定,主观性较强,因此,本文在针对物料配送路径优化问题进行研究的同时,提出了一种基于粒子群算法调参的混合蚁群算法:首先,引入动态调整惯性因子的粒子群算法以确定蚁群算法的初始参数,代替传统依靠经验取参的方法;其次,针对蚁群算法在算法中期容易停滞的现象,改进了蚁群算法的状态转移方程,增大探索新解的概率;最后,利用狼群分食原则对信息素更新规则进行改进,提高收敛速度。比较有效的解决了上述问题。
1 问题描述及其数学模型的构建
某电器公司以生产中大型开关柜为主,客户需求总的来说呈现出小批量、多品种的特点,使得生产工艺比较复杂,生产装配过程中需要大量的零部件供应。但是在实际生产中,由于生产工艺仍沿用着传统的物料配送方式,补充零部件不及时,导致生产效率低下,因此亟需优化物料配送方式。
车间物料配送需要满足各工位对时间窗的需求,时间窗即时间段,表示物料只能在规定的时间段内送达,太早导致线边库存积压,太晚则不能满足及时生产的需求。由于每个工位的生产节拍不同,同一时间需要的物料也不尽相同,同时由于送料车本身有容量限制,不能一次性满足所有工位的物料需求,就需要在尽可能满载的情况下准时给多个有需求的工位提供物料,并满足最短送料总路径、最少送料车的条件。
假设生产车间有N个工位,物料配送部门有V辆载重均为C的物料配送车,目标函数:
(1)
s.t.
(2)
(3)
(4)
(5)
(6)
tei≤ti≤tli(i=1,2,…,N)
(7)
其中,i,j为工位节点,为0时表示仓库;v为送料车代号;dij为工位i到工位j的距离;xijv为决策变量,当送料车v从工位i到工位j依次送料时为1,否则为0;yiv为决策变量,当送料车v完成工位i的送料时为1,否则为0;ci表示第i个工位的物料需求量;ti为送料车到达工位i的时间,tei和tli分别为允许送料车到达工位i的最早时间和最晚时间。
式(1)为目标函数,表示物料配送路径的最小值;式(2)表示每次由一辆送料车完成各个需求点的物料配送;式(3)表示送料车单次配送量不得超过其核载;式(4)表示所有送料车均从仓库出发;式(5)表示送料车完成送料后返回仓库;式(6)表示到达每个工位的送料车数与离开的相等,即网络流平衡;式(7)为时间窗限制。
2 改进的蚁群算法
蚁群算法是模拟自然界中蚁群找寻最短路径觅食的过程,蚂蚁通过分泌信息素来实现蚁群内的合作,其他蚂蚁受其附近的信息素影响,倾向于沿着浓度更高的路径觅食,从而影响到本身的行进路线。较短路径上的蚂蚁越来越多,该路径上的信息素越来越浓,增大了其他蚂蚁选择该路线的可能性,如此反复,最终实现蚁群统一在最短路线上采食。
可以看出,影响蚂蚁走向的是信息素和蚂蚁自身决策,这种决策称为启发式信息,信息素使群体的结果收敛,启发式信息作为个体对其他可能路径的探索。蚂蚁v从节点i移动到j的可能性称为状态转移概率,在基本蚁群算法中,表示如下:
(8)
式中,t表示算法迭代次数,τij(t)表示路径i到j上的信息素浓度,ηij(t)表示启发式函数,α为信息素启发因子,β是期望启发因子;allowedv表示蚂蚁可以选择的节点集合,allowedv=N-tabuv,N为所有节点的集合,tabuv表示蚂蚁已经访问过的节点。启发式函数η和信息素浓度τ更新函数分别如下:
(9)
τij(t+1)=ρτij(t)+Δτij
(10)
式中,dij表示节点i到j的距离;ρ∈[0,1]表示信息素挥发系数,通常设τij(0)为常数,Δτij表示遍历完所有节点后,所有蚂蚁在节点i到j的路径上所释放信息素的剩余总量,即:
其中,Δτij表示第v只蚂蚁在经过路径i到j时释放的信息素,有蚁周模型、蚁量模型和蚁密模型三种更新方式:
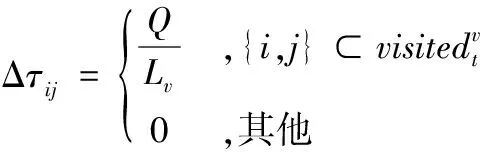

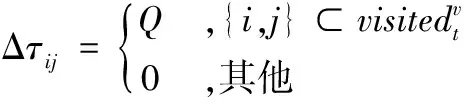
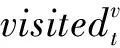
2.1 选择概率的改进
按照式(8)状态转移概率方程可以发现,整个蚁群搜索过程稳定在一个比较大的范围,这有利于算法迭代初期增大蚁群选择较优解的概率、加快算法的收敛速度,但是在算法的中期,搜索进入了停滞状态,因为算法陷入了局部最优的困境。因此,有必要增加蚂蚁探索新解的可能性,从而逃离困境。
在蚂蚁进行下一步路径更新之前,进行一次随机选择,这个选择决定蚂蚁是按照状态转移概率来实现对已知信息的利用,还是无视信息进行新路径的探索。引入概率阈值q0∈(0,1),以此来决定利用和探索的占比,蚂蚁选择的下一节点则可以表示为:
式中,随机变量q∈[0,1],J表示按照基本蚁群算法的选择概率蚂蚁将要移动的下一节点。显然,通过控制q0的值即可决定是利用累积信息还是搜索新路径。在算法初期需要蚁群积累有效信息,实现较快的收敛速度,故可将q0的值调大;到了算法中期,通过将q0值设置为较小值来扩大搜索空间;到了后期,恢复q0为初始值,再次加快收敛速度。具体实现如下:
其中,NCmax为最大迭代次数。
2.2 基于狼群分食原则改进信息素更新
狼群捉住猎物之后,首先由强壮的狼分食,然后才轮到瘦弱的狼,这样才能保证狼群拥有持续捕杀新猎物的能力。基于这样一种“先强后弱”的原则,对信息素更新模型进行优化,在每次循环中选出局部最优、最差路径上的蚂蚁,并确定其数量,增大最优蚂蚁的影响力,淘汰最差蚂蚁释放的信息素,以此来提高算法的收敛速度。得出的信息素浓度更新公式如下:
(11)
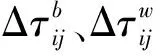
2.3 基于粒子群算法的参数优化
蚁群算法模型中,参数的选择对算法的收敛性和全局寻优影响明显,本文针对式(8)状态转移概率方程中的参数信息素启发因子α和期望启发因子β、式(10)信息素浓度更新模型中的信息素挥发系数ρ和蚁周模型中的信息素常量Q这4个参数进行选择方法的优化。在传统蚁群算法中,参数组的确定多为依据实验,而这四个参数联系紧密,难以用数学模型进行统一描述,本文采用粒子群算法(Particle Swarm Optimization,PSO)进行参数组的最终确定。
粒子群算法是由埃伯哈特和肯尼迪在1995年提出的一种进化计算技术,具有易于实现、精度高、收敛速度快的特点[9]。粒子群算法通过观察动物群体行为,共享群体中的个体信息,使整个集群的无序运动在问题解空间中逐渐演变为有序,从而得到较好的结果。PSO通过迭代在随机解中进行寻优,根据适应度评估解的质量,它通过遵循当前最优值来找到全局最优解[10]。PSO速度和位置的更新公式如下:
(12)
(13)
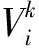
在蚁群算法的参数优化中,将粒子定义为四维坐标,初始坐标值分别对应蚁群算法的待优化参数α、β、ρ、Q,然后将寻优后的坐标反馈给蚁群算法进行路径规划,将得到的最短路径长度作为粒子群算法的评价函数。改进蚁群算法的详细步骤如下:
步骤1:初始化全局参数,如迭代次数k、粒子的数量N、位置X、粒子速度Vi和上述其他系数;
步骤2:将蚁群算法的4个待确定参数α、β、ρ、Q粒子作为位置向量的4个维度,运行蚁群算法开始路径规划;
步骤3:将步骤2得到的最短路径的倒数作为粒子群算法的评价函数,更新个体最优值Pib和全局最优值G;
步骤4:根据式(12)和式(13)更新粒子的位置和速度,其中惯性因子采用动态调整的方法,从而提高运行速度,调整方法如下:
式中,f为目标函数值,fmin表示粒子群的最小值,favg则为平均数;
步骤5:if迭代次数未完成,跳至步骤2;else,算法结束,全局最优粒子的坐标即最佳参数。算法流程图如图1所示。
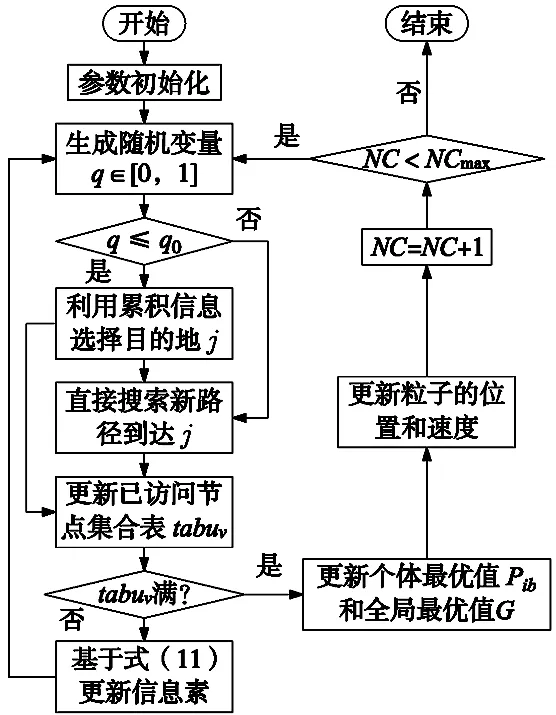
图1 改进蚁群算法流程图
3 实例验证
以某电气柜装配车间的物料配送为例,采用第二章所述数学模型,利用第三章改进的蚁群算法,结合车间的现场数据进行配送路径优化,实验数据见表1、表2。本次实验基于MATLAB-R2014a进行编程,运行环境为:Windows 10(64位OS),内存8 GB,处理器为英特尔酷睿i5-6300HQ @2.30 GHz。
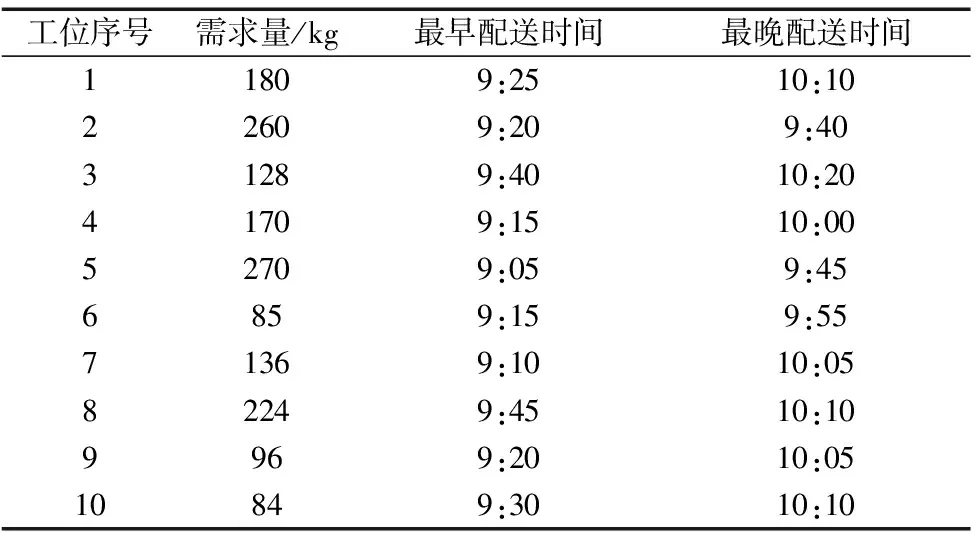
表1 物料需求表

表2 工位距离表
首先设置实验参数。蚁群算法的循环次数取NCmax=100,蚂蚁数量设置为节点的1.5倍,即15,α、β、ρ、Q由粒子群算法确定最终值,此次试验设定范围为:α∈[1,4],β∈[3,4.5],ρ∈[0.4,0.8],Q∈[10,100];粒子群算法中,粒子越多,搜索范围越广,越容易找到全局最优解,但也会导致计算时间更长,本次实验取25,c1、c2均取1.496 1,ωmax=0.95,ωmin=0.4。
粒子群算法迭代10次得出的蚁群算法最佳参数组合基本稳定在一个范围内,最终取值为:α=1.15、β=3.46、ρ=0.87、Q=74.65。作为对比,将参数组分别应用到改进蚁群算法和传统蚁群算法中,运行10次,求出的结果见表3。
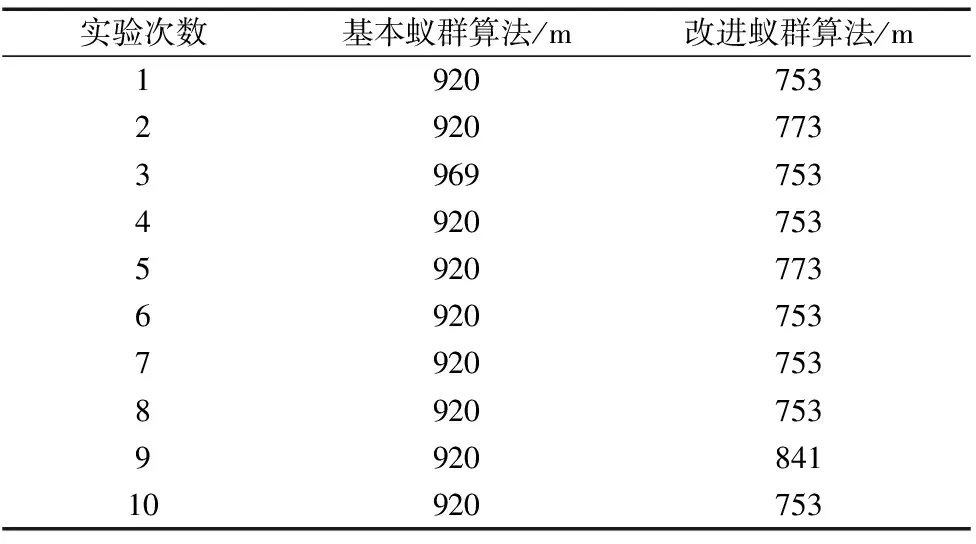
表3 两种算法的最优结果
10次试验中,基本蚁群算法的最优解有9次稳定在920 m,最优路径为0-2-1-3-0-7-6-4-9-10-0-5-8-0,三次运输的装载率分别为94.67%、95.17%、82.3%;改进蚁群算法的最优解有7次稳定在753 m,最优路径为0-2-1-3-0-5-6-4-0-7-9-10-8-0,三次运输的装载率分别为94.67%、87.5%、90%,可以看出,改进的蚁群算法具有比基本算法更好的优化能力。取第7次试验的结果作为对比,改进算法和基本算法的收敛轨迹对比图如图2所示。
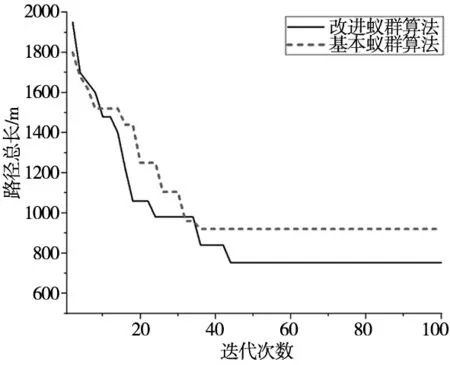
图2 两种算法的收敛轨迹
可以看出,迭代前期改进算法的收敛速度大于基本蚁群算法,在迭代到前中期后,基本蚁群算法结束了寻优,而改进算法在陷入了一段停滞后搜索到了更优的解。通过动态调整粒子群算法的惯性因子,改进算法运行的总时间减少至稍大于基本算法,符合工厂的实际生产需求。
4 结束语
本文基于多品种、小批量的生产特点建立了物料配送路径优化的数学模型,根据模型的特点提出一种改进的蚁群算法进行求解,算法改进了状态转移概率,并基于狼群分食的原则进行信息素的更新。结尾通过一个实例对模型和算法进行仿真,结果表明模型对解决实际路径优化问题是可行的,改进蚁群算法在实际工程应用允许的时间延迟下,寻优效果提升明显,整体性能优于传统蚁群算法,具有一定的理论和实践价值。
