蚁狮算法在第二类多目标装配线平衡问题中的应用*

陈 帅，晁永生，江 韩

(新疆大学机械工程学院，乌鲁木齐 830047)

0 引言

装配线平衡研究主要被分为两大类：一种是给定生产线节拍，以最小工作站数目为优化目标的第一类装配线平衡问题[1]；另一种是给定装配线工作站数，以最小生产节拍为优化目标的第二类装配线平衡问题[2]。第一类装配线平衡问题只产生在设计一条新的装配线时，而每当现有的装配线做出调整需要重新达到平衡时，第二类装配线平衡问题就会随之产生[3]，而且随着企业装配环境的复杂化，往往需要对第二类装配线平衡问题的多个目标进行优化。

在实际装配生产中、每个任务完成装配所需的零部件存储在对应工位的零部件放置区，由于不同任务所需的零部件尺寸范围跨度大，造成不同工位的占地面积具有很大差异，不便于物流运输与人员行走，导致物流运输效率低下增加不必要的时间成本，因此应考虑任务所需的占地面积，合理分配任务到工位上使得每个工位的占地面积相对均匀。同时在重新规划装配线时，某些工位会增加新的任务因此工人需要学习如何装配新的任务，而不同的任务，装配难度是不同的，因此对应所需要花费的学习成本也不同，所以当工位增加新的任务时会带来学习成本的增加，为了降低企业重新调整装配线的总成本，在优化其他目标的同时应该尽可能最小化学习成本。因此面临特定的装配环境时需要考虑对多个目标同时进行优化以保证求解结果满足实际的生产需求。

蚁狮算法[4](Ant Lion Algorithm,ALA)是一种新型智能群算法，具有寻优效率高，全局搜索寻优能力强等优点，目前已在多个领域[5-7]内得到了应用，并且取得了不错的效果，本文在单目标蚁狮算法的基础上提出一种多目标蚁狮算法(Multi-objective Ant Lion Algorithm,MOALA)，运用于第二类多目标装配线平衡问题的求解。通过对实例算例求解并与改进多目标粒子群算法对比分析，验证该算法的有效性和优越性。

1 第二类多目标装配线平衡问题的数学模型

1.1 问题描述

为了简化问题,只考虑任务分配过程中所需的零部件占地面积不同，合理分配任务到工位上使得各工位的占地面积相对均衡，同时最小化工位的生产节拍以提高生产效率，并且尽可能降低调整后的装配分配方案带来的学习成本。

某企业实例装配作业任务的任务信息和调整前后的装配方案如表1所示，给定的工位数目为3。调整前后装配方案的节拍分别为17，15，每个工位所需占地面积分别为[48.2,46.7,12.8]，[37.2,27.3,43.2]，可知调整后的装配方案较调整前在节拍和占地面积均衡性上都要好，但是由于工位2和工位3增加了新的任务，所以也带来了学习成本，新增加的任务为任务6与任务3,4，所以学习成本的累积和是17。

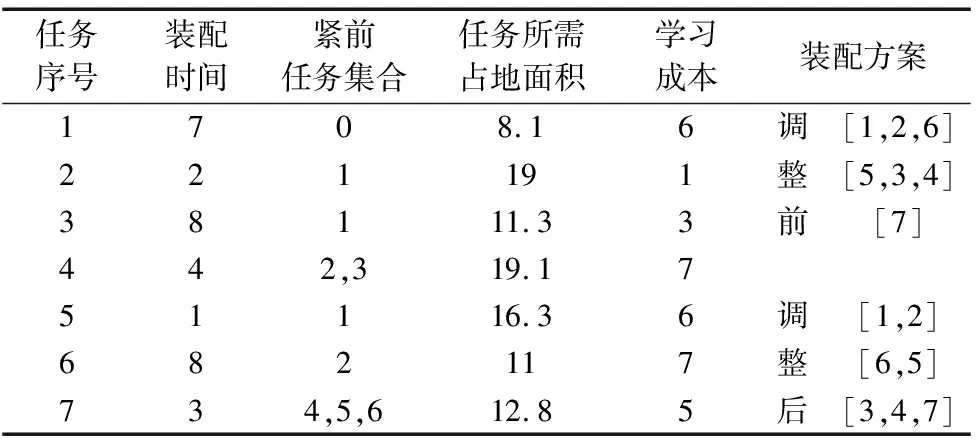
表1 任务信息与调整前后的装配方案

本文以最小化生产节拍、学习成本，占地面积均衡指标为目标建立第二类多目标装配线平衡问题的优化模型，假设：①每个任务都有稳定的任务时间且学习成本和所需的占地面积都是固定的；②必须将所有的任务都分配到工位中；③工位个数是确定的；④任务的分配不能违反优先关系约束。

1.2 数学模型

变量及其含义定义如下：n为任务数；m为工位数；I为任务矩阵，I=(1,2,…,n)为行向量，由所有任务序号构成；t(i)为任务i的操作时间，Cost(i)为任务i的学习成本，Area(i)为任务i所需要的占地面积，i为I内任务；Pdn×n为优先关系矩阵，如果任务i1是i2的优先任务，Pd(i2,i1)=1，否则为0；J为工位矩阵，J=(1,2,…,m)由所有I中的元素构成；j为J内元素；ST(j)为工位j的装配时间；Sq(j)表示工位j所分配到的任务集合。

CT为装配线节拍：

CT=max{ST(1),ST(2),…,ST(m)}

(1)

CtTheory为装配线节拍的理论值：

(2)

WArea(j)为工位j的占地面积：

WArea(j)=∑(Area(Sq(j)))

(3)

其中，MArea为所有工位当中最大的占地面积：

MArea=max(WArea(1),…,WArea(m))

(4)

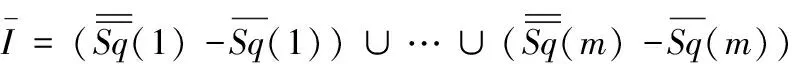
(5)

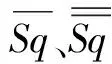
决策变量：

xij，0-1变量，当任务i被分配到第j个工位时，xij=1，否则xij=0。

目标函数：

Z={Z1,Z2,Z3}

(6)

Z1=minCT

(7)

(8)

(9)

约束条件：

(10)

ST(j)≤CT

(11)

(12)

模型说明：式(6)表示同时优化3个目标值；其中优化目标Z1如式(7)所示最小化工位的生产节拍；优化目标Z2如式(8)所示，最小化由每个工位新增加的操作任务带来的学习成本；优化目标Z3如式(9)所示最小化工位占地面积均衡指标使得空间面积得到合理化的应用。式(10)表示每个任务只能与一个工作站相匹配，不能进行重复分配；式(11)表示生产节拍约束，每个工位的操作时间都应小于或等于生产节拍；式(12)表示优先关系约束。其中式(10)～式(12)对应的3种约束被称为装配线平衡的基本约束。

2 求解第二类多目标装配线平衡问题的蚁狮

算法

求解第二类多目标装配线平衡优化问题，难点在于确保最优解集的均匀性和多样性，本文在单目标蚁狮算法的基础上提出一种多目标蚁狮算法用于求解该问题，通过引入解码和基于牛顿二分法的解码装配任务分配规则，使得每个个体均满足装配线平衡的基本约束；引入Pareto支配规则，确保得到的精英蚁狮群为最优解集，为了保证最优解集的均匀性和多样性，去除单目标蚁狮算法中的蚁狮捕食规则而是将蚂蚁和蚁狮种群合并成新种群并且引入基于非支配排序和拥挤度的精英保留策略更新蚁狮种群的位置。多目标蚁狮算法的流程如图1所示。

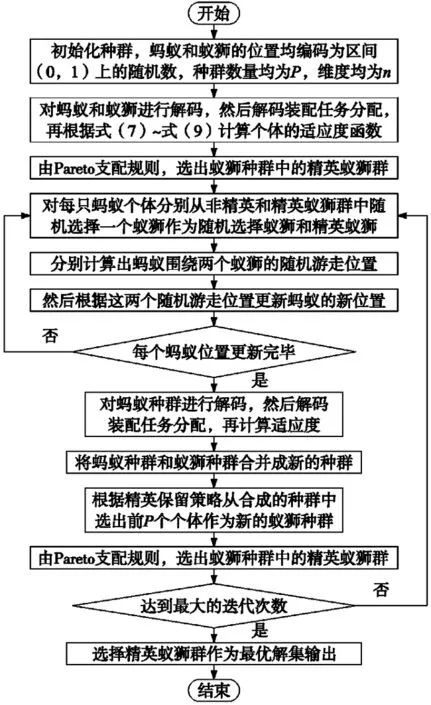
图1 多目标蚁狮算法流程图

2.1 解码和基于牛顿二分法的解码装配任务分配

假设个体的位置为向量PosList，输出的任务序列矩阵为TaskList，对于PosList的解码采用文献[8]中基于位置优先权重的解码方法，通过结合位置向量和优先关系矩阵将个体的位置解码为对应的任务序列矩阵。为求解任务序列矩阵TaskList的最优分配节拍，利用牛顿二分法的思想不断将节拍搜索区间一分为二从而快速将任务分配到工位上，得出最优分配节拍CT和任务分配集合Sq，解码装配任务分配流程如图2所示。

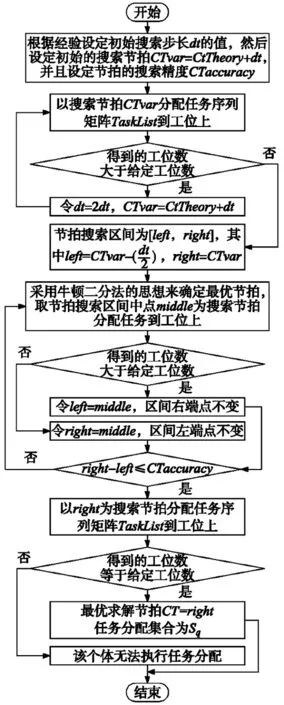
图2 解码装配任务分配流程图

2.2 Pareto支配规则和精英保留策略

在多目标优化问题中，往往存在多个目标之间构成相互冲突的关系，通常不可能找到一个最优解使得每个目标函数都达到最优，因此解的优劣性采用文献[9]中的Pareto支配规则来衡量,对于无法执行任务分配的个体直接设置为最劣个体，由Pareto支配规则选择蚁狮种群中的最优解集为精英蚁狮群。采用文献[10]中基于非支配排序和拥挤度的精英保留策略选择出新的蚁狮群，种群数量均为P的蚂蚁种群Pt和蚁狮种群Qt合并成种群数量为2P的Rt，先对Rt中的个体非支配排序分层，分层完毕之后，对每一层的个体计算拥挤度，最后根据每个个体的优劣程度从种群Rt中选出前P个个体形成新的蚁狮种群。

3 实例验证

为验证算法的性能，以某企业的实际问题为例优化求解，给定工位数目m=3，任务信息如表1所示。并与改进的多目标粒子群算法[11](Multi-objective Improved Particle Swarm Algorithm,MIPSA)对比分析，使用以下指标对算法进行综合衡量：

(1)非劣解数目：表示算法搜索Pareto最优解的能力。

(2)世代距离[12]：表示所求的Pareto最优解距真实Pareto最优解的运近程度。

(3)间隔[13]：表示所求的Pareto最优解中各个解的均布程度。

(4)运行时间：表示算法运行一次所需的时间。

由于问题的可行解空间规模巨大，难以得到真实的最优解集，因此取各算法求出的最优解集作为所求问题的真实最优解集。经过算法的灵敏性实验，设置算法相关参数：种群数目P=300，最大迭代次数tmax=300；初始搜索步长dt=10，节拍搜索精度CTaccuracy=0.01。为消除随机因素的影响，各算法取100次的平均结果对4个指标对比说明。

由表2可知多目蚁狮算法在4个指标上均比改进多目标粒子群算法更优，表明在单目标蚁狮算法中去除蚁狮捕食规则的基础上加入Pareto支配规则与基于非支配排序和拥挤度的精英保留策略之后，多目标蚁狮算法不仅在搜索Pareto最优解的能力上相比于改进多目标粒子群算法更强而且所求得的最优解集不仅更靠近于真实的最优解集而且在均布程度上也比其他两种算法更优，在运行时间上由于多目标蚁狮算法的迭代更新机制比改进多目标粒子群算法的复杂度更低，所以用更短的时间即可求出更优的Pareto解集。

表2 4种指标比较

在表3中列出了100次求解结果中两种算法求解出的各目标函数最小值，并且列出了多目标蚁狮算法中3个目标函数最小值的求解方案进行说明，可知多目标蚁狮算法搜索出的3个目标函数最小值均比改进多目标粒子群算法搜索出的值都要小，再次表明多目标蚁狮算法搜索出的最优解集更接近于真实的最优解集。结合表2和表3可知多目标蚁狮算法能在更短时间内为企业提供更多且更优的装配方案。

表3 求解结果

4 结论

通过对实际问题的求解，并与改进多目标粒子群算法对比分析，表明多目标蚁狮算法在搜索Pareto最优解的能力上相比于改进多目标粒子群算法更强；所求得的最优解集不仅更靠近于真实的最优解集而且在均布程度上也比改进多目标粒子群算法更优，在运行时间上也更短。从而说明了多目标蚁狮算法在求解第二类多目标装配线平衡优化问题的适用性和优越性。